回帰問題とは、数値を予測するための機械学習の手法の一つです。一般的には線形回帰や決定木ベースの手法(XGBoost、LightGBMなど)が用いられますが、深層学習(Deep Learning)を活用することでより複雑な関係を学習し、高精度な予測が可能になります。
今回は、深層学習を使った回帰問題の解決手法について紹介します。
深層学習とは
深層学習(Deep Learning)は、人工知能(AI)や機械学習(Machine Learning)の分野において急速に発展している技術の一つです。特に、大量のデータを分析し、パターンを学習する能力が非常に優れています。
従来の機械学習では、人が特徴量(データの重要な要素)を設計する必要がありましたが、深層学習では自動で特徴を抽出し、複雑なデータ構造を学習することができます。これにより、画像認識、音声認識、自然言語処理、ゲームAIなど、様々な分野で驚異的な成果を上げています。
機械学習 vs 深層学習
機械学習は、数百~数千件のデータがあれば、ある程度の予測精度を持つモデルを比較的短時間に得ることができます。しかし、複雑なパターンの学習は苦手であり、学習に使う特徴量は、あらかじめ指定しなければなりません。
一方、深層学習は、非常に複雑なデータパターンでも高精度な予測が可能ですが、、数十万~数百万のデータが必要であり、膨大な計算量のためにGPUなどの計算リソースが不可欠です。
下記の比較表をもとに、機械学習 vs 深層学習におて、最適な方法を選択します。
| 比較項目 | 機械学習(例: 線形回帰、決定木、SVM、XGBoost) | 深層学習(例: ニューラルネットワーク、CNN、RNN) |
|---|---|---|
| データ量 | 比較的少ない〜中程度のデータ量でも効果を発揮しやすい | 大量のデータがある場合に高い性能を発揮しやすい(データ量が多いほど有利) |
| 特徴量 | 人間が手動で特徴量を設計・抽出できる場合に適している | データから自動的に特徴量を学習・抽出する場合に適している(特に非構造化データ) |
| 問題の複雑さ | データ間の関係が比較的単純〜中程度の非線形性の場合 | データ間の関係が非常に複雑で、高度な非線形性を持つ場合 |
| 解釈性 | モデルの予測根拠を比較的容易に解釈・説明できる | モデルの内部構造が複雑なため、解釈が難しい傾向がある(ブラックボックス) |
| 計算資源 | 学習に必要な計算資源が比較的少ない(CPUでも十分な場合が多い) | 学習に多くの計算資源(GPUなど)と時間を必要とすることが多い |
| 得意なデータ | 表形式データ、数値データ、カテゴリデータなど | 画像、音声、テキスト、時系列データなどの非構造化データ、高次元データ |
| 一般的なアプローチ | まず最初に試す候補として、シンプルなモデルから始めることが多い | シンプルなモデルで精度が不足する場合や、データが非構造化データの場合に検討する |
| 機械学習が有利なケース | 深層学習が有利なケース |
|---|---|
| データ量が少ない 特徴量が明確で人間が設計できる モデルの解釈性が重要 計算資源が限られている 非線形性がそこまで複雑ではない | データ量が非常に多い場合 特徴量の抽出が困難(特徴量を自動で学習したい) データ間の関係が非常に複雑で非線形 高精度が最優先される 時系列データや連続的なデータ |
多くの回帰問題では、まずは線形回帰、決定木、XGBoostなどの比較的シンプルな機械学習モデルから試すのが一般的です。これで十分な精度が得られれば、それがベストな選択です。
データ量が少なく、特徴量が明確な場合は機械学習。データ量が膨大で、特徴量設計が困難、かつ複雑なパターンを持つ場合は深層学習を検討します。
深層学習で回帰問題を解くアプローチ
深層学習で回帰問題を解くアプローチ 深層学習にはさまざまなモデルがありますが、回帰問題に適したアプローチは以下のようなものがあります。
| モデル | 特徴 | 適用例 |
|---|---|---|
| MLP(多層パーセプトロン) | シンプルな全結合型ニューラルネットワークで非線形関係を学習可能 | センサー値予測、金融データ分析 |
| LSTM / GRU(リカレントニューラルネットワーク) | 時系列データの依存関係を考慮できる | 気象予測、株価予測 |
| Transformer | 長期的なパターンを捉えるためのSelf-Attention機構 | 高度な時系列データ分析、センサーデータ予測 |
| CNN(畳み込みニューラルネットワーク) | 局所的な特徴を抽出し、時系列データや画像データに応用可能 | 振動データ解析、画像ベースの回帰問題 |
| オートエンコーダ(AE) | データの特徴抽出と次元削減を活用した回帰手法 | 異常検知、データ補完 |
| グラフニューラルネットワーク(GNN) | グラフ構造を持つデータの関係性を学習 | 交通流予測、ソーシャルネットワークの影響分析 |
深層学習モデル作成時の注意点
深層学習モデルを作成する際には、いくつかの重要な注意点があります。適切な設計や学習方法を採用しないと、過学習や計算コストの増大などの問題が発生することがあります。以下に、モデル構築時の主な注意点を解説します。
データの前処理
モデルの精度はデータの質に大きく依存するため、適切な前処理が必須です。
- 標準化・正規化:データのスケールを統一(例:Min-Maxスケーリング、Zスコア正規化)。
- 欠損値の処理:欠損値を適切に補完するか、除外する。
- 特徴量選択:不要な特徴を削減し、モデルの学習を効率化。
- データ分割:学習データ、検証データ、テストデータを適切な割合で分割(例:80%学習、10%検証、10%テスト)。
モデルの設計
深層学習モデルの構造は慎重に設計しないと、過学習や計算コストの問題が発生することがあります。
- 層の深さ:浅すぎると表現力が不足し、深すぎると計算コストが増加。
- ニューロンの数:適切なニューロン数を設定し、計算負荷と性能のバランスを取る。
- 活性化関数:ReLU、tanh、sigmoid などを適切に選択。
- ドロップアウト:過学習を防ぐために一定割合のニューロンをランダムに無効化。
学習の最適化
学習プロセスを適切に管理しないと、モデルの収束が遅くなることがあります。
- 学習率の調整:学習率が高すぎると収束が不安定になり、低すぎると収束が遅くなる。
- バッチサイズの調整:小さいバッチはノイズが多いが一般化しやすく、大きいバッチは安定するがメモリ消費が増える。
- エポック数の設定:適切なエポック数で学習を止める(早すぎると未学習、長すぎると過学習)。
- オプティマイザの選択:SGD, Adam, RMSprop などの選択によって学習の挙動が変わる。
モデルの評価
正しく評価しないと、過学習や汎化性能の低下が見落とされる可能性があります。
- 損失関数の選択:回帰なら MSE(平均二乗誤差)、分類ならクロスエントロピーなど。
- 評価指標の設定:MAE, RMSE, R² などの適切な指標を用いる。
- 交差検証:データの分割方法を変えてモデルの汎化性能をチェック。
- 過学習のチェック:学習データと検証データの損失の差を監視。
実運用時の考慮
モデルの開発後も、運用に向けた設計を検討する必要があります。
- 推論速度:運用環境において推論時間が許容範囲内か確認。
- モデルの軽量化:量子化や蒸留を行い、エッジデバイス対応を考慮。
- 更新と再学習:定期的に新しいデータでモデルを再学習し、性能を維持。
- 異常検知:予測の異常値を適切に検知し、誤動作を防ぐ。
回帰問題の解き方
事前準備(ライブラリ導入とデータ準備)
事前に下記4つのライブラリをインストールしてください。
pip install numpy
pip install pandas
pip install tensorflow
pip install scikit-learn
下記は今回の回帰に使うダミーデータの生成プログラムです。7つの特徴量のデータとなります。
一般的に、深層学習モデルを作成する際の教師データとして、1000件は少なすぎるかもしれませんが、今回は手法の解説が目的であるため、計算速度を考慮して、あえて件数を少なくしています。
import numpy as np
import pandas as pd
# 特徴量の数
n_features = 7
# 各特徴量の標準偏差
std_devs = [1, 1, 1, 1, 1, 1, 1]
# 相関行列の設定(例: 1番目と2番目の特徴量が強い相関を持つ)
correlation_matrix = np.array([
[1, 0.8, 0.2, 0.1, 0.1, 0.1, 0.1],
[0.8, 1, 0.3, 0.2, 0.2, 0.2, 0.2],
[0.2, 0.3, 1, 0.4, 0.3, 0.3, 0.3],
[0.1, 0.2, 0.4, 1, 0.5, 0.5, 0.5],
[0.1, 0.2, 0.3, 0.5, 1, 0.4, 0.4],
[0.1, 0.2, 0.3, 0.5, 0.4, 1, 0.3],
[0.1, 0.2, 0.3, 0.5, 0.4, 0.3, 1]
])
# 共分散行列の計算
covariance_matrix = np.outer(std_devs, std_devs) * correlation_matrix
# ダミーデータの生成
np.random.seed(42)
n_samples = 1000
data = np.random.multivariate_normal(np.zeros(n_features), covariance_matrix, size=n_samples)
# DataFrameに変換
df = pd.DataFrame(data, columns=[f'特徴量_{i+1}' for i in range(n_features)])
# 結果の確認
print(df.head())
# CSVファイルに保存
df.to_csv('regression_data.csv', index=False)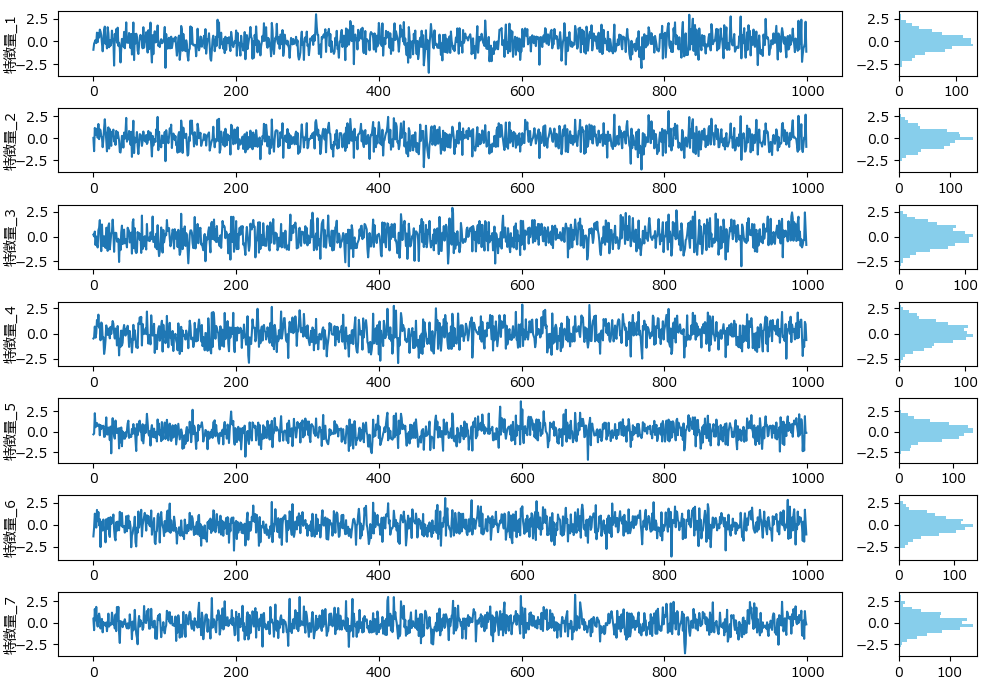
MLPを使った回帰モデルの学習と評価(サンプルコードと解説)
MLPは、全結合層を積み重ねたシンプルなニューラルネットワークであり、非線形な関係を学習するのに適しています。特に、比較的少量のデータでも動作可能であり、調整しやすいモデルとして広く利用されています。
ただし、最低1000〜5000サンプル程度が必要であり、データが少なすぎる場合は過学習しやすい点に注意が必要です。
import pandas as pd
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score, mean_absolute_percentage_error
def train_mlp_regressor(df, target, columns, test_size=0.2, random_state=42, epochs=20, batch_size=16):
"""
MLP(多層パーセプトロン)回帰モデルを学習し、評価指標を出力する関数。
"""
columns = [col for col in columns if col != target]
X = df[columns].values
y = df[target].values.reshape(-1, 1)
# データ分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state)
# 標準化(スケーリング)
scaler_X = StandardScaler()
scaler_y = StandardScaler()
X_train = scaler_X.fit_transform(X_train)
X_test = scaler_X.transform(X_test)
y_train = scaler_y.fit_transform(y_train)
y_test = scaler_y.transform(y_test)
# MLPモデル定義(3層)
model = keras.Sequential([
layers.Dense(64, activation='relu', input_shape=(X_train.shape[1],)),
layers.Dense(32, activation='relu'),
layers.Dense(1) # 出力層(回帰)
])
# モデルコンパイルと学習
model.compile(optimizer='adam', loss='mse')
model.fit(X_train, y_train, epochs=epochs, batch_size=batch_size, verbose=0)
# 予測
y_pred = model.predict(X_test)
y_pred = scaler_y.inverse_transform(y_pred)
y_test = scaler_y.inverse_transform(y_test)
# 評価指標の計算
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
mape = mean_absolute_percentage_error(y_test, y_pred)
# 精度評価の表示
print('\n精度評価:')
print(f'平均絶対誤差 (MAE): {mae:.4f}')
print(f'平均二乗誤差 (MSE): {mse:.4f}')
print(f'ルート平均二乗誤差 (RMSE): {rmse:.4f}')
print(f'平均絶対パーセンテージ誤差 (MAPE): {mape:.4f}')
print(f'決定係数 (R²): {r2:.4f}')
return model # MLPモデルのみを返す
if __name__ == "__main__":
# データ読み込みとMLP学習
df = pd.read_csv('regression_data.csv')
model = train_mlp_regressor(df,target='特徴量_1',columns=df.columns)精度評価:
平均絶対誤差 (MAE): 0.4902
平均二乗誤差 (MSE): 0.3845
ルート平均二乗誤差 (RMSE): 0.6201
平均絶対パーセンテージ誤差 (MAPE): 2.3050
決定係数 (R²): 0.6604
LSTMを使った回帰モデルの学習と評価
LSTMは、時系列データや長期間の依存関係を学習するのに適したリカレントニューラルネットワーク(RNN)です。
特に、過去の情報を保持しながら未来を予測する能力に優れ、金融やセンサー解析などの分野で広く利用されています。
ただし、最低3000〜5000サンプル程度が必要であり、データが少なすぎると、長期的な依存関係を十分に学習できず精度が低下する可能性があるため注意が必要です。
import pandas as pd
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score, mean_absolute_percentage_error
def train_lstm_regressor(df, target, columns, time_steps=10, test_size=0.2, random_state=42, epochs=20, batch_size=16):
"""
LSTM(リカレントニューラルネットワーク)回帰モデルを学習し、評価指標を出力する関数。
"""
columns = [col for col in columns if col != target]
X = df[columns].values
y = df[target].values.reshape(-1, 1)
# データを時系列型に変換(LSTM用)
X_series = []
y_series = []
for i in range(len(X) - time_steps):
X_series.append(X[i:i+time_steps])
y_series.append(y[i+time_steps])
X_series = np.array(X_series)
y_series = np.array(y_series)
# データ分割
X_train, X_test, y_train, y_test = train_test_split(X_series, y_series, test_size=test_size, random_state=random_state)
# 標準化(スケーリング)
scaler_X = StandardScaler()
scaler_y = StandardScaler()
X_train = scaler_X.fit_transform(X_train.reshape(-1, X_train.shape[-1])).reshape(X_train.shape)
X_test = scaler_X.transform(X_test.reshape(-1, X_test.shape[-1])).reshape(X_test.shape)
y_train = scaler_y.fit_transform(y_train)
y_test = scaler_y.transform(y_test)
# LSTMモデル定義
model = keras.Sequential([
layers.LSTM(64, activation='relu', return_sequences=True, input_shape=(time_steps, X_train.shape[2])),
layers.LSTM(32, activation='relu'),
layers.Dense(1)
])
# モデルコンパイルと学習
model.compile(optimizer='adam', loss='mse')
model.fit(X_train, y_train, epochs=epochs, batch_size=batch_size, verbose=0)
# 予測
y_pred = model.predict(X_test)
y_pred = scaler_y.inverse_transform(y_pred)
y_test = scaler_y.inverse_transform(y_test)
# 評価指標の計算
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
mape = mean_absolute_percentage_error(y_test, y_pred)
# 精度評価の表示
print('\n精度評価:')
print(f'平均絶対誤差 (MAE): {mae:.4f}')
print(f'平均二乗誤差 (MSE): {mse:.4f}')
print(f'ルート平均二乗誤差 (RMSE): {rmse:.4f}')
print(f'平均絶対パーセンテージ誤差 (MAPE): {mape:.4f}')
print(f'決定係数 (R²): {r2:.4f}')
return model # LSTMモデルのみを返す
if __name__ == "__main__":
# データ読み込みとLSTM学習
df = pd.read_csv('regression_data.csv')
model = train_lstm_regressor(df, target='特徴量_1', columns=df.columns)精度評価:
平均絶対誤差 (MAE): 0.9044
平均二乗誤差 (MSE): 1.2144
ルート平均二乗誤差 (RMSE): 1.1020
平均絶対パーセンテージ誤差 (MAPE): 1.7169
決定係数 (R²): -0.0827
Transformerを使った回帰モデルの学習と評価
Transformerは、自己注意機構(Self-Attention)を活用し、時系列データや複雑な関係をモデル化するのに適した深層学習アーキテクチャです。
特に、LSTMのような再帰的構造を持たず並列処理が可能であり、大量のデータを効率的に学習できます。
ただし、最低5000〜10000サンプル以上のデータが必要であり、データが少ない場合は、過学習や意味のあるパターンが学習されにくい問題が発生するため、適切な正則化や事前学習の活用が推奨されます。
import pandas as pd
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score, mean_absolute_percentage_error
def train_mlp_regressor(df, target, columns, test_size=0.2, random_state=42, epochs=20, batch_size=16):
columns = [col for col in columns if col != target]
X = df[columns].values
y = df[target].values.reshape(-1, 1)
# データ分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state)
# 標準化
scaler_X = StandardScaler()
scaler_y = StandardScaler()
X_train = scaler_X.fit_transform(X_train)
X_test = scaler_X.transform(X_test)
y_train = scaler_y.fit_transform(y_train)
y_test = scaler_y.transform(y_test)
# MLPモデル
model = keras.Sequential([
layers.Dense(64, activation='relu', input_shape=(X_train.shape[1],)),
layers.Dense(32, activation='relu'),
layers.Dense(1) # 出力層(回帰)
])
model.compile(optimizer='adam', loss='mse')
model.fit(X_train, y_train, epochs=epochs, batch_size=batch_size, verbose=0)
# 予測と評価
y_pred = model.predict(X_test)
y_pred = scaler_y.inverse_transform(y_pred)
y_test = scaler_y.inverse_transform(y_test)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
mape = mean_absolute_percentage_error(y_test, y_pred)
print(f'\n精度評価:')
print(f'平均絶対誤差 (MAE): {mae:.4f}')
print(f'平均二乗誤差 (MSE): {mse:.4f}')
print(f'ルート平均二乗誤差 (RMSE): {rmse:.4f}')
print(f'平均絶対パーセンテージ誤差 (MAPE): {mape:.4f}')
print(f'決定係数 (R²): {r2:.4f}')
return model
if __name__ == "__main__":
df = pd.read_csv('regression_data.csv')
model = train_mlp_regressor(df, target='特徴量_1', columns=df.columns)精度評価:
平均絶対誤差 (MAE): 0.4965
平均二乗誤差 (MSE): 0.3966
ルート平均二乗誤差 (RMSE): 0.6298
平均絶対パーセンテージ誤差 (MAPE): 2.1603
決定係数 (R²): 0.6497
CNNを使った回帰モデルの学習と評価
CNN(畳み込みニューラルネットワーク)は、局所的な特徴抽出に優れたモデルであり、画像データだけでなく時系列データやセンサー情報の回帰予測にも適用できます。
特に、畳み込み層を活用して特徴を抽出し、データのパターンを捉えやすくするメリットがあります。
ただし、最低3000〜5000サンプル以上のデータが推奨されており、データが少なすぎると過学習のリスクが高まるため、適切な正則化やプーリング層を活用することが重要です。
また、カーネルサイズやフィルター数を適切に調整しないと、不要な特徴を学習し精度が低下する可能性がある点にも注意が必要です。
import pandas as pd
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score, mean_absolute_percentage_error
def train_cnn_regressor(df, target, columns, time_steps=10, test_size=0.2, random_state=42, epochs=20, batch_size=16):
"""
CNN(畳み込みニューラルネットワーク)を利用した回帰モデルを学習し、評価指標を出力する関数。
"""
columns = [col for col in columns if col != target]
X = df[columns].values
y = df[target].values.reshape(-1, 1)
# 時系列データ変換(CNN用)
X_series = []
y_series = []
for i in range(len(X) - time_steps):
X_series.append(X[i:i+time_steps])
y_series.append(y[i+time_steps])
X_series = np.array(X_series)
y_series = np.array(y_series)
# データ分割
X_train, X_test, y_train, y_test = train_test_split(X_series, y_series, test_size=test_size, random_state=random_state)
# 標準化
scaler_X = StandardScaler()
scaler_y = StandardScaler()
X_train = scaler_X.fit_transform(X_train.reshape(-1, X_train.shape[-1])).reshape(X_train.shape)
X_test = scaler_X.transform(X_test.reshape(-1, X_test.shape[-1])).reshape(X_test.shape)
y_train = scaler_y.fit_transform(y_train)
y_test = scaler_y.transform(y_test)
# CNNモデル構築
model = keras.Sequential([
layers.Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(time_steps, X_train.shape[2])),
layers.MaxPooling1D(pool_size=2),
layers.Conv1D(filters=32, kernel_size=3, activation='relu'),
layers.GlobalAveragePooling1D(),
layers.Dense(64, activation='relu'),
layers.Dense(1) # 出力層(回帰)
])
model.compile(optimizer='adam', loss='mse')
model.fit(X_train, y_train, epochs=epochs, batch_size=batch_size, verbose=0)
# 予測
y_pred = model.predict(X_test)
y_pred = scaler_y.inverse_transform(y_pred)
y_test = scaler_y.inverse_transform(y_test)
# 評価指標の計算
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
mape = mean_absolute_percentage_error(y_test, y_pred)
# 精度評価の表示
print('\n精度評価:')
print(f'平均絶対誤差 (MAE): {mae:.4f}')
print(f'平均二乗誤差 (MSE): {mse:.4f}')
print(f'ルート平均二乗誤差 (RMSE): {rmse:.4f}')
print(f'平均絶対パーセンテージ誤差 (MAPE): {mape:.4f}')
print(f'決定係数 (R²): {r2:.4f}')
return model # CNNモデルのみを返す
if __name__ == "__main__":
df = pd.read_csv('regression_data.csv')
model = train_cnn_regressor(df, target='特徴量_1', columns=df.columns)精度評価:
平均絶対誤差 (MAE): 1.0593
平均二乗誤差 (MSE): 1.5744
ルート平均二乗誤差 (RMSE): 1.2548
平均絶対パーセンテージ誤差 (MAPE): 2.9636
決定係数 (R²): -0.4036
オートエンコーダ(AE)を使った回帰モデルの学習と評価
オートエンコーダ(AutoEncoder, AE)は、データの特徴を圧縮して学習し、その情報を回帰タスクに活用するモデルです。
特に、高次元データやノイズの多いデータに対して、重要な特徴のみを抽出し、より精度の高い予測が可能になる利点があります。
ただし、最低2000〜5000サンプル以上のデータが推奨されており、データが少なすぎると、特徴抽出の効果が限定され、汎化性能が低下する可能性があるため注意が必要です。
また、エンコーダの次元を適切に設定しないと、情報が失われすぎてしまうことがあるため、ハイパーパラメータの調整が重要になります。
適用例として、異常検知や特徴量の圧縮を伴う回帰タスクなどに活用できます。
import pandas as pd
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score, mean_absolute_percentage_error
def train_autoencoder_regressor(df, target, columns, encoding_dim=16, test_size=0.2, random_state=42, epochs=20, batch_size=16):
"""
オートエンコーダ(AE)を利用した回帰モデルを学習し、評価指標を出力する関数。
"""
columns = [col for col in columns if col != target]
X = df[columns].values
y = df[target].values.reshape(-1, 1)
# データ分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state)
# 標準化
scaler_X = StandardScaler()
scaler_y = StandardScaler()
X_train = scaler_X.fit_transform(X_train)
X_test = scaler_X.transform(X_test)
y_train = scaler_y.fit_transform(y_train)
y_test = scaler_y.transform(y_test)
# オートエンコーダ(AE)構築
input_dim = X_train.shape[1]
# エンコーダ
input_layer = layers.Input(shape=(input_dim,))
encoded = layers.Dense(32, activation='relu')(input_layer)
encoded = layers.Dense(encoding_dim, activation='relu')(encoded)
# デコーダ
decoded = layers.Dense(32, activation='relu')(encoded)
decoded = layers.Dense(input_dim, activation='sigmoid')(decoded)
# AEモデル定義
autoencoder = keras.Model(input_layer, decoded)
# 回帰モデル(エンコーダの出力を使って予測)
regressor = keras.Sequential([
layers.Dense(64, activation='relu', input_shape=(encoding_dim,)),
layers.Dense(32, activation='relu'),
layers.Dense(1) # 出力層(回帰)
])
# AEの学習
autoencoder.compile(optimizer='adam', loss='mse')
autoencoder.fit(X_train, X_train, epochs=epochs, batch_size=batch_size, verbose=0)
# エンコーダから特徴抽出
encoder = keras.Model(inputs=input_layer, outputs=encoded)
X_train_encoded = encoder.predict(X_train)
X_test_encoded = encoder.predict(X_test)
# 回帰モデルの学習
regressor.compile(optimizer='adam', loss='mse')
regressor.fit(X_train_encoded, y_train, epochs=epochs, batch_size=batch_size, verbose=0)
# 予測
y_pred = regressor.predict(X_test_encoded)
y_pred = scaler_y.inverse_transform(y_pred)
y_test = scaler_y.inverse_transform(y_test)
# 評価指標の計算
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
mape = mean_absolute_percentage_error(y_test, y_pred)
# 統計情報の表示
print(f'{target} の統計情報:')
print(f'最小値 (Min): {y.min()}')
print(f'最大値 (Max): {y.max()}')
print(f'平均値 (Mean): {y.mean()}')
print(f'標準偏差 (Std): {y.std()}')
print(f'分散 (Var): {y.var()}')
# 精度評価の表示
print('\n精度評価:')
print(f'平均絶対誤差 (MAE): {mae:.4f}')
print(f'平均二乗誤差 (MSE): {mse:.4f}')
print(f'ルート平均二乗誤差 (RMSE): {rmse:.4f}')
print(f'平均絶対パーセンテージ誤差 (MAPE): {mape:.4f}')
print(f'決定係数 (R²): {r2:.4f}')
return autoencoder, regressor # AEモデルと回帰モデルを返す
if __name__ == "__main__":
df = pd.read_csv('regression_data.csv')
autoencoder, regressor = train_autoencoder_regressor(df, target='特徴量_1', columns=df.columns)精度評価:
平均絶対誤差 (MAE): 0.5345
平均二乗誤差 (MSE): 0.4643
ルート平均二乗誤差 (RMSE): 0.6814
平均絶対パーセンテージ誤差 (MAPE): 2.4923
決定係数 (R²): 0.5899
グラフニューラルネットワーク(GNN)を使った回帰モデルの学習と評価
グラフニューラルネットワーク(GNN)は、ノード間の関係を学習するのに適したモデルであり、特にセンサー情報や複雑なデータ構造を持つ回帰タスクに有効です。
通常のニューラルネットワークとは異なり、隣接関係を考慮することで、データの構造を忠実に学習できる特徴があります。
ただし、最低1000〜5000サンプル程度のデータが推奨されており、グラフ構造が適切でない場合は学習の効果が十分に発揮されないことに注意が必要です。
また、エッジ(関係性)の定義が不適切だと、誤った特徴を学習する可能性があるため、適切なグラフ設計が重要になります。
適用例として、センサーネットワークの異常検知や、交通流の予測、ソーシャルネットワーク分析などに活用できます。
pip install torch torchvision torchaudio
pip install torch-scatter torch-sparse torch-cluster torch-spline-conv
pip install torch-geometric
import pandas as pd
import numpy as np
import torch
import torch.nn.functional as F
from torch_geometric.data import Data
from torch_geometric.nn import GCNConv
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score, mean_absolute_percentage_error
class GNNRegressor(torch.nn.Module):
def __init__(self, in_channels):
super(GNNRegressor, self).__init__()
self.conv1 = GCNConv(in_channels, 64)
self.conv2 = GCNConv(64, 32)
self.fc = torch.nn.Linear(32, 1) # 出力層(回帰)
def forward(self, x, edge_index):
x = F.relu(self.conv1(x, edge_index))
x = F.relu(self.conv2(x, edge_index))
return self.fc(x)
def train_gnn_regressor(df, target, columns, edges, test_size=0.2, random_state=42, epochs=100, lr=0.01):
"""
GNN(グラフニューラルネットワーク)を利用した回帰モデルを学習し、評価指標を出力する関数。
"""
columns = [col for col in columns if col != target]
X = df[columns].values
y = df[target].values.reshape(-1, 1)
# データ分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state)
# 標準化
scaler_X = StandardScaler()
scaler_y = StandardScaler()
X_train = scaler_X.fit_transform(X_train)
X_test = scaler_X.transform(X_test)
y_train = scaler_y.fit_transform(y_train)
y_test = scaler_y.transform(y_test)
# PyTorchテンソルに変換
X_train_tensor = torch.tensor(X_train, dtype=torch.float32)
y_train_tensor = torch.tensor(y_train, dtype=torch.float32)
edge_index = torch.tensor(edges, dtype=torch.long).T # グラフの隣接情報をPyTorch用に変換
# GNNモデルの初期化
model = GNNRegressor(X_train.shape[1])
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
criterion = torch.nn.MSELoss()
# 学習
for epoch in range(epochs):
model.train()
optimizer.zero_grad()
y_pred = model(X_train_tensor, edge_index)
loss = criterion(y_pred, y_train_tensor)
loss.backward()
optimizer.step()
# 予測と評価
model.eval()
X_test_tensor = torch.tensor(X_test, dtype=torch.float32)
y_pred = model(X_test_tensor, edge_index).detach().numpy()
y_pred = scaler_y.inverse_transform(y_pred)
y_test = scaler_y.inverse_transform(y_test)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
mape = mean_absolute_percentage_error(y_test, y_pred)
print('\n精度評価:')
print(f'平均絶対誤差 (MAE): {mae:.4f}')
print(f'平均二乗誤差 (MSE): {mse:.4f}')
print(f'ルート平均二乗誤差 (RMSE): {rmse:.4f}')
print(f'平均絶対パーセンテージ誤差 (MAPE): {mape:.4f}')
print(f'決定係数 (R²): {r2:.4f}')
return model # GNNモデルのみを返す
if __name__ == "__main__":
df = pd.read_csv('regression_data.csv')
# グラフのエッジ情報(センサー間の関連付け)
edges = [
[0, 1], [1, 2], [2, 3], [3, 4], [4, 0], # 例:センサー同士の接続関係
]
model = train_gnn_regressor(df, target='特徴量_1', columns=df.columns, edges=edges)精度評価:
平均絶対誤差 (MAE): 0.4922
平均二乗誤差 (MSE): 0.4089
ルート平均二乗誤差 (RMSE): 0.6395
平均絶対パーセンテージ誤差 (MAPE): 2.7090
決定係数 (R²): 0.6388
予測精度の改善
アンサンブル学習(例えばXGBoost)は決定木の数や木の深さ、学習率などのハイパーパラメータの調整が重要ですが、深層学習の場合はネットワークの構造自体(層の深さや幅)を調整することが大きなポイントになります。
深層学習では、層を増やしすぎると過学習のリスクがあるため、以下のような基準で調整します。
深層学習の予測精度を改善するポイント
- モデルの構造を最適化
層の数やニューロン数を適切に調整(シンプルなモデルから試し、必要なら深くする)
過学習を防ぐために Dropout や Batch Normalization を導入
ResNetやスキップ接続を使い、勾配消失を軽減 - データの前処理を強化
標準化(StandardScaler)や正規化(MinMaxScaler)で入力データを調整
関係の薄い特徴量を削除し、重要な特徴に絞る
外れ値を適切に処理し、モデルの安定性を向上 - ハイパーパラメータの調整
学習率の調整(高すぎると収束が不安定、低すぎると学習が遅い)
バッチサイズを適切に設定(一般に32~256が最適)
活性化関数(ReLU, Leaky ReLU, Swishなど)を試しながら最適化 - 過学習の防止
早期停止(Early Stopping)で、無駄な学習を防ぐ
正則化(L2正則化, Dropout)でモデルの汎化性能を向上
データ拡張(Augmentation)で学習データを増やし、ノイズ耐性を向上 - アンサンブル学習の活用
複数のモデル(MLP + XGBoost など)を組み合わせて精度向上
異なるアーキテクチャ(LSTM, CNN, Transformer)を統合し、多様な特徴を学習
モデルの予測結果を平均化し、安定した結果を得る
まずはシンプルな構造で試し、データ処理やハイパーパラメータの調整をしながら段階的に改善するのが効果的です。
まとめ
深層学習を用いた回帰モデルは、非線形な関係を学習し、高精度な予測を可能にします。
本記事では、MLP(多層パーセプトロン)から始め、LSTM、CNN、Transformer、GNNなどの手法を活用した回帰モデルの構築方法を解説しました。
✅ 機械学習 vs 深層学習:データ量やパターンの複雑さに応じて選択
✅ まずは MLP で試す:シンプルなモデルから始め、調整しながら精度を確認
✅ 最適な手法を選ぶ:時系列なら LSTM、画像データなら CNN、構造化データなら GNN
✅ 予測精度の改善:正則化・データ拡張・ハイパーパラメータ調整で最適化
✅ アンサンブル学習の活用:複数のモデルを組み合わせて精度向上
深層学習を活用した回帰モデルは、試行錯誤しながら最適化することが重要です。まずはシンプルなMLPから試し、データの前処理やパラメータ調整を行いながら精度を高めていきましょう!
もしさらなる改善が必要であれば、適切なモデル選択やアンサンブル学習を活用し、より頑健な予測を目指してください。
今回紹介したコードは、コピペで実行可能なサンプル付きなので、ぜひ実際に動かしながら理解を深めてみてください!









コメント