モーター、ポンプ、減速機——。あらゆる回転系設備のメンテナンスにおいて、避けて通れないのが「ベアリングやギアの異常診断」です。
しかし、初期の摩耗や傷が発する微細な衝撃音は、回転系特有の大きな低周波振動(軸の回転音など)に埋もれやすく、通常のFFT解析だけでは見逃してしまうことが少なくありません。
そこで威力を発揮するのが「エンベロープ解析」です。この手法はベアリングに限らず、ギアの欠けやベルトの損傷など、「周期的な衝撃」が発生するあらゆる回転系メカニズムに応用可能です。
本記事では、Pythonを用いて信号の「包絡線」を取り出し、見えない故障の予兆を可視化する実装プロセスをステップバイステップで解説します。
エンベロープ解析(包絡線解析)とは
エンベロープ解析(包絡線解析)は、一言で言えばデータの中から「繰り返される『コツコツ』という衝撃のリズム」を突き止めるための手法です。
通常のFFTが「どんな高さの音が鳴っているか」を調べるのに対し、エンベロープ解析は「どんな間隔で衝撃が起きているか」を調べます。
エンベロープ解析を、音楽に例えるとメロディか、リズムの違いに相当します。
- エンベロープ解析(リズム分析): 周囲がどれだけ騒がしくても、ドラムが「ドン、ドン」と叩かれる間隔だけに注目します。この「叩く間隔」がわかれば、ベアリングのどの部品に傷があるかを特定できます。
- 通常のFFT(メロディ分析): 「この曲はドとミの音が強い」という音色を分析します。
どうやって分析しているの?
エンベロープ解析は、以下の4ステップで「衝撃の正体」を浮き彫りにします。
- FFT解析: 出来上がった「外形」のリズムをFFTで調べます。象データを一発で計算するため、圧倒的に処理が高速なのが特徴です。
- バンドパスフィルタ: 軸が回る「ゴー」という低い音をカットし、異常の衝撃が含まれる高い共鳴音だけを残します。
- 整流(絶対値化): 波形をプラス側に折り返します。
- ローパスフィルタ: 細かなギザギザをなだらかに結び、波形の「外形(エンベロープ)」を取り出します。
重要なパラメータの決め方は?(バンドパスの帯域とヒルベルト変換)
エンベロープ解析の成否は、「どの帯域を狙い撃ちするか(フィルタ)」と、「どうやって輪郭を抜き出すか(変換)」の組み合わせで決まります。
まずバンドパスフィルタで、異常衝撃が潜んでいる『共鳴帯域』を狙い撃ちし、不要なノイズ(回転音など)を徹底的に排除します。
次に、フィルタを通った波に対してヒルベルト変換を行い、波の絶対値(包絡線)を算出します。
バンドパスフィルタ帯域:SN比を最大化する「窓」の設定
FFTと同様にデータの端での不連続性は問題になりますが、エンベロープ抽出ではそれ以上に「どの周波数帯にフィルタをかけるか」が成否を分けます。異常衝撃によって機械が「キーン」と共鳴している帯域(通常は数kHz以上)を狙い撃ちすることで、SN比が劇的に向上します。
- 決め方のコツ:後述するエンベロープ解析結果グラフに現れる突き抜けが、全体的に最も長くなる帯域をカット&トライで探します。
- 指標: 感覚ではなく、「尖度(Kurtosis)」という数値が最大になる帯域を正解とします。
ヒルベルト変換:計算上の「検波」の仕組み
フィルタで抽出した「キーン」という高周波の波から、その「強弱の輪郭(エンベロープ)」を取り出すのがヒルベルト変換の役割です。
- 仕組み: 元の信号を90度位相シフトさせた「虚数部」を作り、元の信号と合成して複素数(解析信号)にします。その「絶対値(大きさ)」を計算することで、波の山を結んだ滑らかな輪郭線が得られます。
- パラメータ: ヒルベルト変換自体にはユーザーが調整する「値」はありません。しかし、「変換にかける前のフィルタ帯域」が適切でないと、ヒルベルト変換後の輪郭線がノイズだらけになり、解析が失敗します。
エンベロープ解析のメリット
1. 「極めて初期」の微細な異常を検知できる
これが最大のメリットです。ベアリングの傷が非常に小さいうちは、発生するエネルギーが小さいため、通常のFFT(パワースペクトル)では背景ノイズに埋もれて全く見えません。 エンベロープ解析は「音の大きさ」ではなく、衝撃が走った時の「共鳴(キーンという響き)」の有無を捉えるため、耳で聞いても分からないレベルの初期剥離を発見できます。
2. 故障箇所をピンポイントで特定できる
エンベロープスペクトルを計算すると、「1秒間に何回衝撃が起きているか(Hz)」が明確に出ます。
- 100.5Hzなら「外輪の傷」
- 145.2Hzなら「内輪の傷」 というように、ベアリングの型番から計算される理論値と照合することで、「どこが、どの程度悪いのか」を分解前に特定できます。
3. AI(機械学習)との相性が抜群に良い
生の振動データをそのままAIに学習させるのは困難ですが、エンベロープ解析によって抽出された「衝撃の鋭さ(尖度)」や「周期性」は、異常検知モデルの極めて優秀な特徴量(インプット)になります。これにより、判定精度の高い予知保全システムを構築しやすくなります。
エンベロープ解析のデメリット(注意点)
1. 事前の「バンドパスフィルタ」設定にノウハウが必要
エンベロープ解析を行う前には、必ず「どの周波数帯の衝撃を見るか」というフィルタ設定(バンドパスフィルタ)が必要です。
- フィルタ帯域が低すぎると、軸の回転振動(ノイズ)を拾いすぎて失敗します。
- 帯域が高すぎると、信号が弱すぎて検知できません。 機械ごとに「どのあたりで共鳴が起きるか」を把握する必要があり、FFTほど「ボタン一つで一発回答」とはいきません。
2. 「傷」以外の衝撃も拾ってしまう
エンベロープ解析は「衝撃(バースト信号)」に非常に敏感です。そのため、ベアリングの傷だけでなく、以下のものも「異常」として検知してしまうことがあります。
- 隣の機械から伝わってくる衝撃
- ギアの噛み合い音
- 潤滑不足による一時的なパチパチ音 これらを見分けるには、算出された周波数が「理論値と一致するか」を慎重に確認するスキルが求められます。
3. 回転速度(rpm)の変動に弱い
エンベロープ解析は「周期」を見る手法であるため、解析中に回転速度がフラフラと変動してしまうと、スペクトルのピークがぼやけてしまい、正確な診断ができなくなります。可変速モーターなどの場合は、回転数に同期してサンプリングするなどの工夫が必要です。
結論:どう使い分ける?
「まずはFFTで全体の健康診断を行い、特定の箇所に違和感(高周波の盛り上がりなど)を感じたらエンベロープ解析で精密検査をする」という2段構えが、回転系診断のベストプラクティスです。
| 特徴 | 通常のFFT | エンベロープ解析 |
| 得意なこと | 軸の振れ、アンバランス、ガタつき | ベアリングの傷、ギアの欠け、衝撃 |
| 検知のタイミング | 中期〜末期の異常(音が大きい) | 超初期〜中期の異常(微かな衝撃) |
| 難易度 | 低(自動設定でOKなことが多い) | 中(フィルタ帯域の選定が必要) |
エンベロープ解析の実装&活用方法
エンベロープ解析は、単に「波形をきれいにする」だけの手法ではありません。抽出した包絡線(エンベロープ)を「どう料理するか」によって、得られる情報の深さが変わります。
実務においては、以下の4つのステップ(シーン)を使い分けることで、異常の早期発見から原因特定、さらには将来の寿命予測までを一気通貫で行うことが可能になります。
- 【時間軸分析】:生の波形から衝撃の「発生タイミング」と「強さ」を可視化する(検波)。
- 【周波数軸分析】:衝撃の周期(リズム)を解析し、損傷している「部位」を特定する(エンベロープFFT)。
- 【数値化(特徴量抽出)】:衝撃の鋭さを数値に変換し、AI判定やトレンド管理に活用する。
- 【高度な分析(合わせ技)】:STFT(スペクトログラム)等と組み合わせ、複雑な変動の中の異常を捉える。
シミュレーションデータの準備
本章に掲載する出力結果(数値、グラフ)は、下記のシミュレーションデータ生成プログラムを使っています。ご自身で試したい場合は、各プログラムの先頭にこのソースコードを貼り付けてください。
このプログラムは、実際のベアリング故障で発生する「物理現象」を忠実に再現するように設計しています。
データの構造:何を作っているのか?
単なるランダムな数値ではなく、以下の3つの要素を合成して「生の振動データ」を模倣しています。
- 背景雑音:計測環境で必ず混入するランダムなホワイトノイズです。
- 回転ノイズ(低周波):軸の回転(RPM)に伴って発生する「ゴー」という日常的な振動です。
- 衝撃波(バースト信号):ベアリングの傷をボールが叩いた瞬間の「カツッ!」という衝撃です。ここでは、機械が「キーン」と高く響く共鳴周波数(3000Hz)と、それが繰り返される損傷周波数(105.5Hz)を組み合わせています。
import numpy as np
def generate_bearing_fault_data(fs, duration, rpm, fault_freq, resonance_freq=3000):
"""
ベアリングの異常(衝撃)シミュレーションデータを生成する
Parameters:
-----------
fs : int サンプリング周波数 (Hz)
duration : float データ長 (秒)
rpm : float 軸の回転数 (毎分)
fault_freq : float 損傷周波数 (Hz) - 1秒間に衝撃が起きる回数
resonance_freq : float 機械の共鳴周波数 (Hz) - 叩いた時の「キーン」という音
"""
# 時間軸の作成
t = np.linspace(0, duration, int(fs * duration))
# 1. 回転に伴う低周波成分(軸のうねりや振動のベース)
fr = rpm / 60
vibration_base = 0.5 * np.sin(2 * np.pi * fr * t)
# 2. 周期的な衝撃波(損傷によるバースト信号)の生成
impacts = np.zeros_like(t)
# 損傷周波数に基づいた発生タイミング(秒)を算出
impact_times = np.arange(0, duration, 1/fault_freq)
for start_t in impact_times:
idx = int(start_t * fs)
if idx < len(t):
# 衝撃発生時の減衰振動(共鳴音)をシミュレート
# 1回あたりの衝撃の長さを約20ms程度とする
length = min(int(fs * 0.02), len(t) - idx)
time_segment = np.linspace(0, length/fs, length)
# 指数関数的に減衰する高い周波数のサイン波
impact_wave = np.sin(2 * np.pi * resonance_freq * time_segment) * np.exp(-500 * time_segment)
impacts[idx:idx+length] += impact_wave
# 3. 全体的な背景ノイズの加算
np.random.seed(42) # 再現性のためにシードを固定
noise = np.random.normal(0, 0.2, len(t))
# すべてを合成して「生の振動データ」を模倣する
raw_data = vibration_base + impacts + noise
return t, raw_data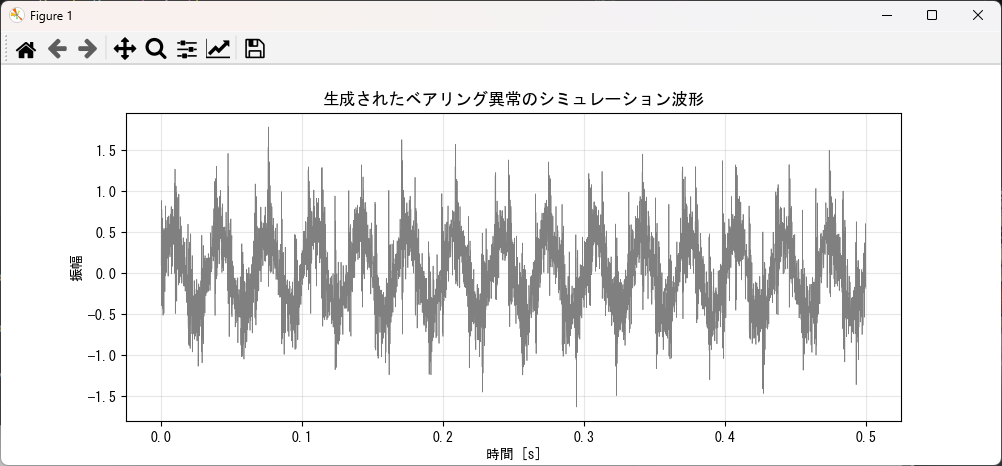
上記グラフを表示したい場合は、上記ソースコードの末尾に張り付けて実行してください。
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
# --- 動作確認 ---
if __name__ == "__main__":
FS = 10000 # 10kHz
DUR = 0.5 # 表示用に短めの0.5秒
RPM = 1800 # 30Hz
BPFO = 105.5 # 外輪損傷の理論値
t, data = generate_bearing_fault_data(FS, DUR, RPM, BPFO)
plt.figure(figsize=(10, 4))
plt.plot(t, data, color='gray', linewidth=0.5)
plt.title("生成されたベアリング異常のシミュレーション波形")
plt.xlabel("時間 [s]")
plt.ylabel("振幅")
plt.grid(True, alpha=0.3)
plt.show()【時間軸分析】隠れた衝撃波形を可視化する(検波)
生の振動データには、回転軸のうねりや周囲の環境ノイズが大量に含まれています。ベアリングの傷が発する「カツッ!」という微細な衝撃は、これらに埋もれてしまい、そのままでは目視で確認することすら困難です。
そこで行われるのが、通信技術でも使われる「検波(デモジュレーション)」という処理です。
高周波の共鳴成分(搬送波)の中に隠された、異常のリズム(信号成分)を「包絡線」として取り出すことで、異常が「いつ」「どの程度の強さで」発生しているかを時間軸上でクリアに可視化できます。
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['font.family'] = 'MS Gothic'
# =====================================================================================
# --- 1. シミュレーションデータ生成関数 ---
# ここに前述した generate_bearing_fault_data 関数を貼り付けて実行してください
# =====================================================================================
# --- 2. エンベロープ解析ロジック ---
def run_envelope_analysis(raw_data, fs, lowcut=2000, highcut=4500):
"""
バンドパスフィルタ + ヒルベルト変換によるエンベロープ抽出
"""
nyq = 0.5 * fs
b, a = signal.butter(4, [lowcut/nyq, highcut/nyq], btype='band')
filtered = signal.filtfilt(b, a, raw_data)
# ヒルベルト変換で包絡線を抽出
envelope = np.abs(signal.hilbert(filtered))
# エンベロープFFT用のスペクトル計算
envelope_detrend = envelope - np.mean(envelope)
n = len(raw_data)
f_axis = np.fft.fftfreq(n, d=1/fs)
spec = np.abs(np.fft.fft(envelope_detrend)) / (n / 2)
return envelope, f_axis[:n//2], spec[:n//2]
# --- 3. グラフ可視化関数 ---
def plot_diagnostic_results(f_axis, spec, theoretical_freq, title="エンベロープFFT解析結果"):
"""
解析結果をプロットし、理論値(BPFO等)と比較する
"""
plt.figure(figsize=(10, 5))
plt.plot(f_axis, spec, color='red', label='エンベロープスペクトル')
# 理論値の補助線
plt.axvline(theoretical_freq, color='blue', linestyle='--', alpha=0.7,
label=f'理論値: {theoretical_freq}Hz')
plt.title(title)
plt.xlabel("周波数 [Hz](=衝撃のリズム)")
plt.ylabel("振幅")
plt.xlim(0, 500) # 診断に重要な低周波域を拡大
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
# --- メイン処理 ---
if __name__ == "__main__":
# パラメータ設定
FS = 10000
DUR = 1.0
RPM = 1800
BPFO_TARGET = 105.5 # 解析の標的となる外輪損傷周波数
# Step 1: データ生成
t, raw_sig = generate_bearing_fault_data(FS, DUR, RPM, BPFO_TARGET)
# Step 2: 解析実行
env, f, s = run_envelope_analysis(raw_sig, FS, lowcut=2000, highcut=4500)
# Step 3: 結果表示
plot_diagnostic_results(f, s, BPFO_TARGET)| パラメータ名 | 今回の設定値 | 設定の理由・根拠 | 実務での決め方 |
|---|---|---|---|
| FS (Sampling Rate) | 10000 (10kHz) | 衝撃波(数kHzの共鳴)を捉えるのに十分な速度を確保するため。 | 捉えたい共鳴周波数の2.5倍〜5倍程度に設定します。通常は5.12kHzや10.24kHz、25.6kHzなどが一般的です。 |
| DUR (Duration) | 1.0 (1秒) | 周波数解像度を1Hzにするため。また、十分な回数の衝撃(105回分)を含めるため。 | 低速回転の場合はもっと長く(3秒〜5秒など)取る必要があります。FFTの解像度(Δf=1/DUR)を意識して決めます。 |
| RPM (Rotations Per Min) | 1800 (30Hz) | 一般的な4極モーターの同期速度(60Hz地域)を想定。 | 実際の回転計の計測値、またはインバーターの設定周波数から入力します。 |
| BPFO_TARGET | 105.5 (Hz) | 今回のベアリング型番とRPMから計算される、外輪損傷時の衝撃リズムの理論値。 | ベアリングの型番ごとに決まっている「幾何係数」に回転周波数を掛けて算出します。カタログ値や専用計算アプリを使います。 |
| lowcut / highcut | 2000 / 4500 | 回転由来の低周波ノイズを避け、機械の「キーン」という共鳴帯域(2k〜5kHz付近)を狙い撃ちするため。 | ここが解析のキモです。 通常のFFTで山が盛り上がっている帯域や、センサーの共振周波数付近を指定します。 |
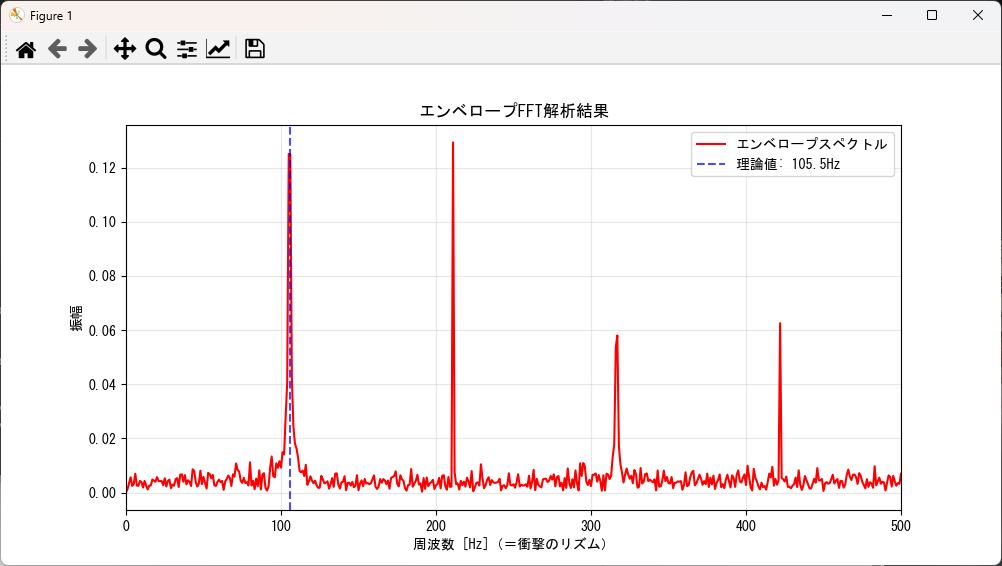
実務で最も重要なのは、lowcut と highcut の調整です。ヒルベルト変換自体は計算式に過ぎませんが、その前処理であるバンドパスフィルタで「何を抽出するか」が結果のすべてを決めます。
低域ノイズの排除: 軸回転などの「大きなうねり」が残っていると、ヒルベルト変換は微小な衝撃ではなく、そのうねりを包絡線として拾ってしまいます。lowcut を適切に設定して、衝撃の「特等席」を確保するのが成功の秘訣です。
「突き抜け」を探す: もしスペクトルのピークが背景ノイズに埋もれて見える場合は、この数値を少しずつずらし、後述する『SN比(突き抜け具合)』が最大になるポイントを探してください。
【周波数軸分析】衝撃の「リズム」を特定する(エンベロープFFT)
時間軸で衝撃の存在を確認できたら、次は「その衝撃がどこから来ているのか」という真犯人の特定に移ります。ここで威力を発揮するのが、抽出した包絡線(エンベロープ)に対してさらにFFTをかける「エンベロープFFT」です。
通常のFFTの横軸が「音の高さ(Hz)」を意味するのに対し、エンベロープFFTの横軸は「衝撃が発生する頻度(Hz=1秒間に何回叩いているか)」を意味します。
損傷箇所を特定する「計算式」との照合
ベアリングの損傷診断がこれほど強力なのは、機械の寸法と回転数から、異常が発生した際に現れる周波数を理論的に計算できるからです。
- BPFO (Ball Pass Frequency Outer race):外輪に傷がある場合のリズム
- BPFI (Ball Pass Frequency Inner race):内輪に傷がある場合のリズム
- BSF (Ball Spin Frequency):転動体(玉)そのものに傷がある場合のリズム
例えば、計算上のBPFOが10.5Hzだったとします。解析結果のスペクトルに「10.5Hz」の鋭いピークが出現していれば、「原因はベアリングの外輪の損傷だ」と、分解する前にピンポイントで特定できるのです。
診断のポイント:高調波(ハーモニクス)の出現
実務上のデータでは、基本となる周波数(例:10.5Hz)だけでなく、その整数倍(21.0Hz, 31.5Hz...)にもピークが並ぶ「高調波」がよく現れます。これは衝撃が鋭いほど顕著に出るため、「規則正しいクシの歯のようなピーク」が見えたら、それは周期的な異常が発生している決定的な証拠となります。
前項で作ったシミュレーションデータを使い、実際に理論値と合致するかを確認するコードです。
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['font.family'] = 'MS Gothic'
# =====================================================================================
# --- 1. シミュレーションデータ生成関数 ---
# ここに前述した generate_bearing_fault_data 関数を貼り付けて実行してください
# =====================================================================================
# --- 2. エンベロープ解析ロジック ---
def run_envelope_analysis(raw_data, fs, lowcut=2000, highcut=4500):
"""
バンドパスフィルタ + ヒルベルト変換によるエンベロープ抽出
"""
nyq = 0.5 * fs
b, a = signal.butter(4, [lowcut/nyq, highcut/nyq], btype='band')
filtered = signal.filtfilt(b, a, raw_data)
# ヒルベルト変換で包絡線(エンベロープ)を抽出
envelope = np.abs(signal.hilbert(filtered))
return envelope
# --- 3. グラフ可視化関数(周波数軸:特定用) ---
def plot_envelope_spectrum(envelope, fs, theoretical_freq):
"""
エンベロープFFTを実行し、理論値(基本波・高調波)と照合する
"""
n = len(envelope)
# 直流成分(平均値)を引いてからFFTをかけるのがスペクトルを綺麗にするコツ
envelope_detrend = envelope - np.mean(envelope)
# FFT実行
f_axis = np.fft.fftfreq(n, d=1/fs)
spec = np.abs(np.fft.fft(envelope_detrend)) / (n / 2)
# 可視化(正の周波数領域のみ。診断に必要な低周波域 0~500Hz に限定)
mask = (f_axis >= 0) & (f_axis <= 500)
plt.figure(figsize=(10, 5))
plt.plot(f_axis[mask], spec[mask], color='red', label='エンベロープスペクトル')
# 理論値(基本波)に補助線を引く
plt.axvline(theoretical_freq, color='blue', linestyle='--', alpha=0.7,
label=f'理論値: {theoretical_freq}Hz')
# 高調波(2倍, 3倍)にも線を引く(これが並んでいれば異常の確証が持てる)
plt.axvline(theoretical_freq * 2, color='blue', linestyle=':', alpha=0.5, label='高調波 (2x, 3x)')
plt.axvline(theoretical_freq * 3, color='blue', linestyle=':', alpha=0.5)
plt.title("エンベロープFFTによる損傷部位の特定")
plt.xlabel("周波数 [Hz](=衝撃のリズム)")
plt.ylabel("振幅")
plt.legend(loc='upper right')
plt.grid(True, alpha=0.3)
plt.show()
# --- 4. メイン処理 ---
if __name__ == "__main__":
# パラメータ設定
FS = 10000 # サンプリング周波数
DUR = 1.0 # 観測時間
RPM = 1800 # 回転数(30Hz)
BPFO_TARGET = 105.5 # 解析の標的となる外輪損傷周波数の理論値
# Step 1: シミュレーションデータの生成
# ※ generate_bearing_fault_data が定義されている必要があります
t, raw_sig = generate_bearing_fault_data(FS, DUR, RPM, BPFO_TARGET)
# Step 2: エンベロープ(包絡線)の抽出
env = run_envelope_analysis(raw_sig, FS)
# Step 3: 周波数スペクトルの表示と理論値照合
plot_envelope_spectrum(env, FS, BPFO_TARGET)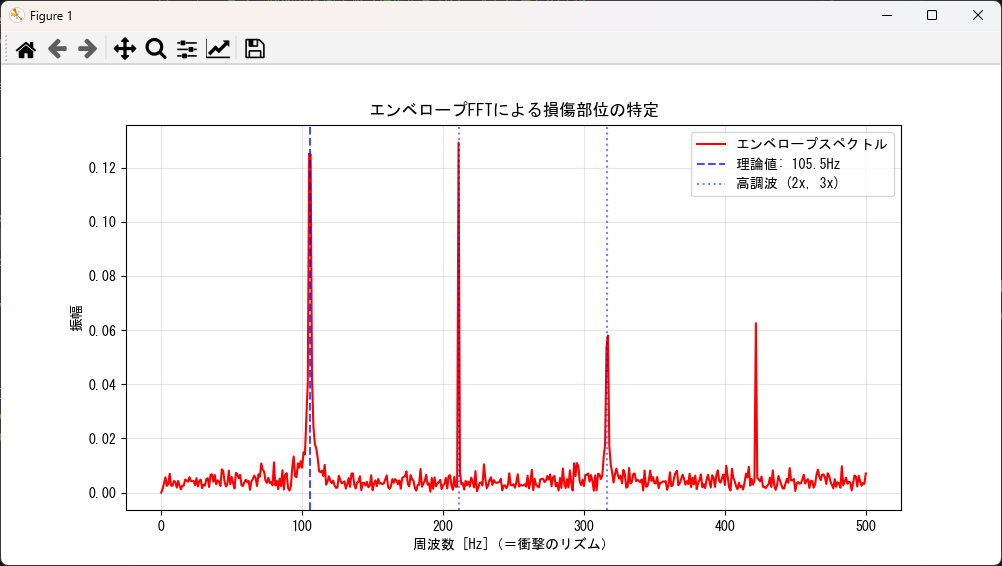
【数値化】異常の「ひどさ」を定量化する(特徴量抽出)
波形やスペクトルを目視で確認するのは確実な方法ですが、数百台の設備を常時監視する場合、人間がすべてをチェックするのは不可能です。そこで重要になるのが、波形の特徴を1つの数値(スカラー値)に圧縮する「特徴量抽出」です。
抽出した特徴量を時系列でプロットすれば、「1ヶ月前から徐々にベアリングの傷が深くなっている」といった傾向管理(トレンド監視)が可能になり、突発的な故障を未然に防ぐことができます。
代表的な3つの指標
エンベロープ波形から「異常のひどさ」を測る際によく使われる指標は以下の通りです。
- 衝撃指数(Impulse Factor)
平均値に対するピークの強さです。クレストファクタと同様に、突発的な変化を捉えるのに適しています。 - 尖度(クルトシス / Kurtosis)
波形の「尖り具合」を示す統計量です。正常時は3に近い値ですが、鋭い衝撃が発生するとこの値が跳ね上がります。初期異常に極めて敏感な指標です。 - クレストファクタ(Crest Factor)
最大値(ピーク)と実効値(RMS)の比率です。全体の振動レベルに対して、どのくらい「突出した衝撃」があるかを示します。
AI(機械学習)への応用
これらの数値は、LightGBMやRandomForestなどのテーブルデータ系AIと非常に相性が良いのが特徴です。 数千点に及ぶ時系列データをそのままAIに入れるのではなく、こうした「意味のある数値」に凝縮して渡すことで、計算コストを抑えつつ、精度の高い異常検知モデルを構築できます。
import numpy as np
from scipy.stats import kurtosis
# =====================================================================================
# --- 1. シミュレーションデータ生成関数 ---
# ここに前述した generate_bearing_fault_data 関数を貼り付けて実行してください
# =====================================================================================
# =====================================================================================
# --- 2. エンベロープ解析ロジック ---
# ここに前述した run_envelope_analysis 関数を貼り付けて実行してください
# =====================================================================================
# --- 3. 特徴量抽出関数(数値化) ---
def extract_envelope_features(envelope):
"""
エンベロープ波形から「異常のひどさ」を示す特徴量を抽出する
"""
# 1. 尖度(Kurtosis): 3に近いほど正常、大きいほど鋭い衝撃(異常)がある
kurt_val = kurtosis(envelope)
# 2. クレストファクタ: 衝撃の鋭さを測る(ピーク値 / 実効値)
rms_val = np.sqrt(np.mean(envelope**2))
crest_factor = np.max(envelope) / rms_val if rms_val > 0 else 0
# 3. 衝撃指数(Impulse Factor): 平均に対するピークの比率
impulse_factor = np.max(envelope) / np.mean(envelope) if np.mean(envelope) > 0 else 0
return {
"Kurtosis": kurt_val,
"CrestFactor": crest_factor,
"ImpulseFactor": impulse_factor
}
# --- 4. メイン処理 ---
if __name__ == "__main__":
# パラメータ設定
FS = 10000
DUR = 1.0
RPM = 1800
BPFO_TARGET = 105.5
# Step 1: 異常データの生成
_, raw_sig = generate_bearing_fault_data(FS, DUR, RPM, BPFO_TARGET)
# Step 2: エンベロープ抽出
env = run_envelope_analysis(raw_sig, FS)
# Step 3: 特徴量の算出
features = extract_envelope_features(env)
# Step 4: 結果の出力
print("-" * 30)
print("エンベロープ特徴量 解析結果")
print("-" * 30)
for key, val in features.items():
print(f"{key:15}: {val:.4f}")
print("-" * 30)
print("※ 正常データなら Kurtosis は 3 前後になります。")エンベロープ特徴量 解析結果
Kurtosis : 1.5719
CrestFactor : 3.6050
ImpulseFactor : 4.4976
※ 正常データなら Kurtosis は 3 前後になります。
【合わせ技】STFT(スペクトログラム)との組み合わせ
ここまで紹介した手法は、主に「一定の回転速度」で「特定の周波数帯」を狙うものでした。しかし、実際の現場では「回転数が常に変動する(可変速制御)」機械や、「複数の異常が同時に起きている」複雑な状況に直面します。
そんな時に有効なのが、以前の記事でも触れたSTFT(短時間フーリエ変換)とエンベロープ解析の組み合わせです。
なぜ組み合わせるのか?
STFT(スペクトログラム)は「どの周波数帯で、いつ音が鳴ったか」を色の濃淡で示します。ここにエンベロープの考え方を加えると、以下のような高度な分析が可能になります。
- 最適なフィルタ帯域の特定
スペクトログラム上で、異常発生時に「縦に一瞬だけ光るライン(衝撃)」が最も強く出ている周波数帯を探します。そこをエンベロープ解析のバンドパスフィルタに設定すれば、最強のSN比で異常を抽出できます。 - 非定常な衝撃の監視
回転数が変化しても、衝撃の発生タイミングがどう変化するかを視覚的に追跡できます。
どの周波数帯に衝撃が隠れているかを「目」で探しながら、同時にエンベロープを確認するコードです。
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
# =====================================================================================
# --- 1. シミュレーションデータ生成関数 ---
# ここに前述した generate_bearing_fault_data 関数を貼り付けて実行してください
# =====================================================================================
# --- 2. 合わせ技解析・可視化関数 ---
def plot_advanced_combined_analysis(data, fs):
"""
STFT(スペクトログラム)とエンベロープを並べて表示し、
異常帯域の特定と包絡線抽出を同時に行う
"""
# 1. STFTの計算(時間・周波数の同時解析)
f, t_stft, Zxx = signal.stft(data, fs, nperseg=256, noverlap=128)
# 2. 比較用のエンベロープ計算
# STFTで見つけた「光る縦線(衝撃)」の帯域(2000-4500Hz)を狙い撃ちします
nyq = 0.5 * fs
b, a = signal.butter(4, [2000/nyq, 4500/nyq], btype='band')
filtered = signal.filtfilt(b, a, data)
envelope = np.abs(signal.hilbert(filtered))
# 3. 可視化
plt.figure(figsize=(12, 8))
# 上段:STFTスペクトログラム
plt.subplot(2, 1, 1)
# パワーをdB表記にすると、微小な衝撃の光る線が見やすくなります
plt.pcolormesh(t_stft, f, 20*np.log10(np.abs(Zxx) + 1e-6), shading='gouraud', cmap='magma')
plt.title("STFTスペクトログラム(縦に走る光る線が衝撃の証拠)")
plt.ylabel("周波数 [Hz]")
plt.colorbar(label="強度 [dB]")
# 下段:抽出されたエンベロープ波形
plt.subplot(2, 1, 2)
t_env = np.linspace(0, len(data)/fs, len(data))
plt.plot(t_env, envelope, color='red', linewidth=1, label="抽出された包絡線")
plt.title("特定帯域(2000-4500Hz)から抽出したエンベロープ波形")
plt.xlabel("時間 [s]")
plt.ylabel("振幅")
plt.legend(loc='upper right')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# --- 3. メイン処理 ---
if __name__ == "__main__":
# パラメータ設定
FS = 10000
DUR = 1.0
RPM = 1800
BPFO_TARGET = 105.5
# Step 1: データの生成
t, raw_sig = generate_bearing_fault_data(FS, DUR, RPM, BPFO_TARGET)
# Step 2: 合わせ技解析の実行
plot_advanced_combined_analysis(raw_sig, FS)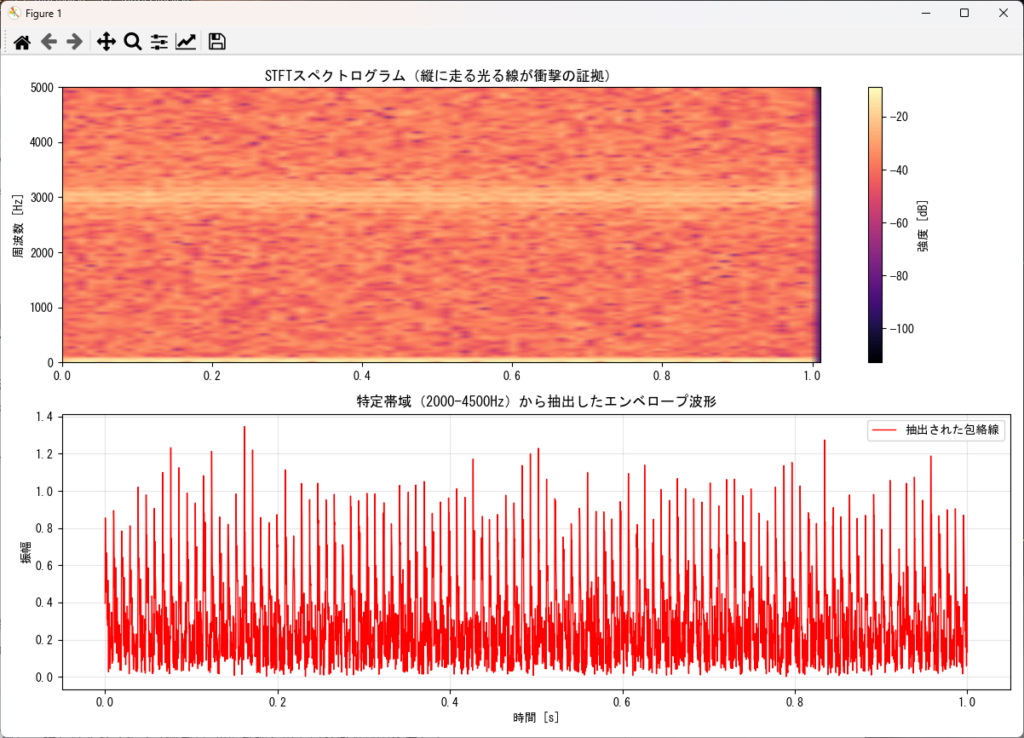
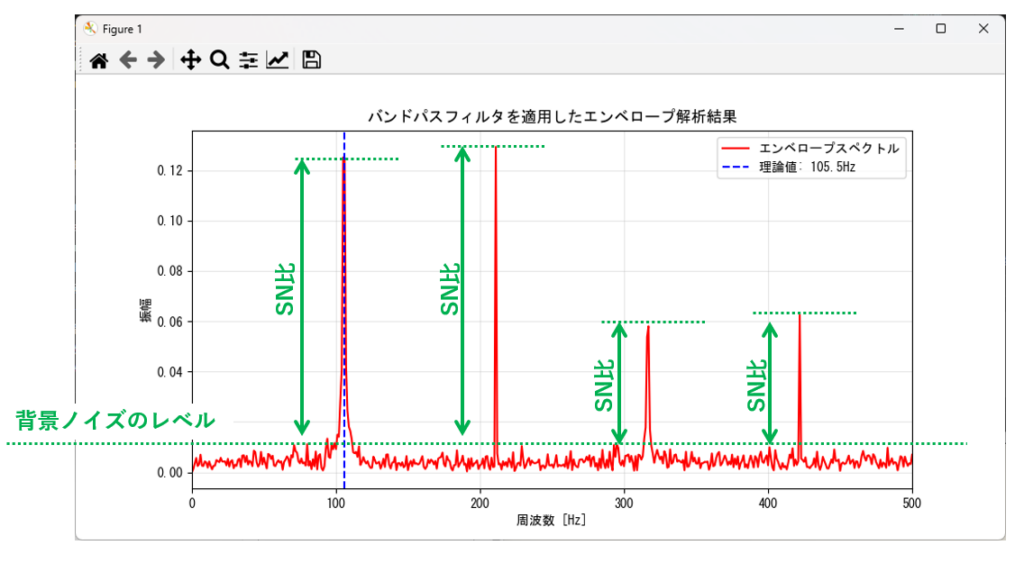
スペクトログラム(上段)を眺めると、2000Hzから5000Hz付近にかけて、等間隔で『縦に光る筋』が走っているのがわかります。これが異常衝撃によって機械がキーンと共鳴している帯域です。この帯域を狙ってフィルタをかけることで、下段のように非常にSN比の良い(衝撃が際立った)エンベロープ波形を取り出すことができます。
バンドパスフィルタ帯域の決め方のコツ
エンベロープ解析の成否は、適切な帯域を選ぶための「試行錯誤」で決まります。一発で決める魔法の数値はなく、以下のループを繰り返して最適なバンドパスフィルタ帯域(lowcut と highcut)を探し出します。
- 最初に最初の帯域を決める
以下の3ステップで最初の帯域を決めます。
①通常のFFTで全体を眺める:異常がない状態と比べて、高周波領域(一般的に2kHz〜10kHz以上)で「山」が盛り上がっている箇所を探します。そこが、衝撃によって機械が「キーン」と共鳴している帯域です。
②回転ノイズを避ける:軸の回転速度の10倍程度の周波数までは、機械全体の振動(ノイズ)が強いため、それより高い帯域(ハイパス)に設定するのが安全です。
③セオリーに従う:一般的には、サンプリング周波数の1/4〜1/2程度の高周波帯域、あるいは加速度センサの共振周波数付近をターゲットにすると、衝撃成分を効率よく抽出できます。 - 解析を実行し、グラフを表示する
次に、その帯域(例:2kHz〜4.5kHz)でプログラムを走らせ、エンベロープスペクトルを描画します。 - グラフを見て「改善」しているか判定する
出力されたグラフの「突き抜け具合(SN比)」をチェックします。
改善(継続)と判断する状態
・背景のノイズが下がり、赤いピークが鋭く突き抜けてきた。
・基本波だけでなく、右側の「高調波」までクッキリ見えてきた。
やり直しと判断する状態
・ピークがノイズに埋もれて判別しにくい。
・低域ノイズが残り、0Hz付近(左端)の大きな山に解析結果が押しつぶされている。 - パラメータを微調整して再解析
判定結果をもとに、lowcutやhighcutを少しずつずらして再度プログラムを実行します。 - ゴール(正解)の基準
ピークが背景から完全に独立し、理論値とピタリと一致すれば「正解」です。
「【時間軸分析】隠れた衝撃波形を可視化する(検波)」では「ピークの位置が理論値と一致するか」に着目していましたが、フィルタ設定の観点では「ピークが背景ノイズからどれだけ際立っているか(SN比)」に着目します。
下記は「正解」のグラフです。実務では一発でここまでくることは稀であり、多くの場合パラメータ調整しながらエンベロープ解析を繰り返すことになります。
まとめ
本記事では、回転系機械の守護神である「エンベロープ解析」の4つの活用シーンを解説しました。
信号処理の基本からAI連携まで、手法を整理すると以下のようになります。
| 知りたいこと・目的 | 推奨されるアプローチ | 得られるアウトプット |
| 「何か変だ」を確認したい | 時間軸分析(検波) | 衝撃の発生タイミング・強さ |
| 「どこが悪いか」を知りたい | 周波数軸分析(FFT) | 損傷部位の特定(BPFOなど) |
| 「自動で監視・判定」したい | 数値化(特徴量抽出) | 尖度・クレストファクタ |
| 「複雑な変動」を分析したい | 合わせ技(STFT併用) | 異常帯域の特定・精密診断 |
データ分析において大切なのは、「目的に合った最適な手法を選択すること」です。
- 継続的な監視には特徴量へ落とし込み、数値の変化を追い続ける。
- まずはFFTで全体の「音の傾向」を大まかに把握する。
- 違和感があればエンベロープ解析へ進み、隠れた「衝撃のリズム」を抽出する。
信号処理の世界は非常に奥が深く、日々試行錯誤の連続です。今回ご紹介したコードや考え方が、皆さんの分析に少しでもお役に立てれば幸いです。








コメント