本記事は「【成功の秘訣】現場で使えるデータ分析手順を体系的に解説」で紹介したデータ探索(事前分析)の具体的な手順と、データの品質を確認するための統計情報の算出、及びグラフ化するためのPythonのサンプルコードを紹介しています。
Pythonのサンプルコードは関数化していますので、コピペしてご利用ください。
尚、GPS位置情報の可視化については「【Python実践】GPS位置情報で車両の軌跡を分析しよう!」に詳細を記載しています。
データ探索(事前分析)の目的

データ探索(事前分析)は、データ自体を理解することです。もう少し具体的に言うと、データの形式と内容を調査し、データに含まれる問題を明確にすることです。
一般的に、次の内容を実施します。
- データの発生元、信頼性の確認
- データ形式の確認
- データ項目の確認
- データの欠損値や異常値の確認
- データの分布や傾向を確認する
データ探索(事前分析)は、探索的分析(EDA=Exploratory Data Analysis)と混同されがちですが、探索的分析は仮説を導き出し、分析方針を選定することが目的です。
とはいうものの、両者は独立しているわけではなく、互いに連携させながら作業を進めることが多いため、これら2つをまとめて探索的分析と表現したり、事前分析と表現することもあります。
データ探索(事前分析)の手順

データの発生元、信頼性の確認
データの値が、どれくらい信頼できるのかを把握するために、データの発生元と信頼性を確認します。
まず最初にデータの発生元を確認します。例えば次の様な内容です。
- センサーから自動収集されたもの
- 業務システム内で計算によって得られたもの
- 他のシステムから自動連係されたもの
- 業務システムに手入力したもの
- 手書きの帳票を誰かが転記したも
次に、データの信頼性を確認します。データの発生元に人手が介在しない場合、例えばセンサーから自動収集されたデータや、業務システムが計算によって生成されたデータは、一見信頼性が高いように見えるかもしれません。
しかし、取り付けに問題があるセンサーや、信頼性の低い他のシステムからのデータ連携の場合、そのデータが信頼できるとは限りません。
また、業務システムに手入力されたデータや誰かが転記したデータでも、二重三重のチェックが施されている場合は、信頼性が高くなります。
したがって、データの発生元とその信頼性を確認することが重要です。
データ形式の確認
データの形式とは、そのデータが格納されている形式です。例えば次のようなデータ形式があります。
| テキストデータ | 作業日誌、取引先リスト、カスタマーレビュー、システムの実行ログなど |
|---|---|
| CSVデータ | 生産品の不良率、センサー値、在庫データなど |
| CSV以外のフォーマットデータ | Json、XMLなど |
| バイナリデータ | 音声、画像、動画など |
| DB | Oracle、PostgreSQL、SQLServer、SQLiteなど |
データ項目の確認
データにはどのようなカラム(列)が含まれており、各カラムの意味が何であるかを確認します。
全てのカラムに対して意味を理解することが理想的ですが、ドメイン知識(業務知識)が必要なため、完全に理解することは難しい場合があります。
まず、ざっくりとデータに目を通し、カラム名やデータの値からおおよその意味を推測します。そして、その推測を基にデータを眺め、そこで生じた疑問点を洗い出します。
例えば、整数4桁の数値が記録されている場合、それはIDかもしれません。また、1と0だけが記録されている場合、それはフラグやカテゴリの可能性があります。
このように思考をめぐらせながらデータを確認していきます。
| カラムの意味 | 各カラムについて、どのような意味を持つのか |
|---|---|
| 発生タイミング | 周期的に発生するのか、何らかの事象に応じて都度発生しているかなど |
| カテゴリの内容 | カテゴリが格納されたカラムの場合、具体的な値(例:1→男、2→女) |
| マスターの有無 | コードやIDが格納されたカラムの場合、どのマスタを参照すべきか |
| その他の注意事項 | 「手入力なので信頼性が低い」、「フリー入力である」など |
データの欠損値や異常値の確認
データに欠損値や異常値があるかどうかを確認します。この段階で見つかった欠損値や異常値については、まだ対策を行いません。理由は、データの分布や傾向によって、欠損値の補完方法や異常値の処理方法が異なるためです。
例えば、欠損値の数が少なければその行を削除するだけで済むかもしれません。しかし、欠損値が多い場合は、前後の値の変化を考慮し、何らかのアルゴリズムで補完する必要があるかもしれません。異常値についても、それがノイズであるならば除外すれば良いですが、重要なデータである場合、除外すると分析結果に影響が出ることがあります。
現段階では、欠損値や異常値がどの項目にどれくらい存在するかを確認することが重要です。欠損値や異常値が多すぎる場合、そのデータが使えないことを分析依頼者に報告し、代替データが手配できるかどうかを確認することも必要です。
データの分布や傾向の確認

データをグラフで可視化し、その分布を確認すると同時に、データが増加しているのか、減少しているのか、または周期性を持って増減を繰り返しているのかを確認します。
この結果を踏まえて、欠損値を含む行を除外するか、または何らかのアルゴリズムで補完するかを考えます。異常値についても同様に、除外すべきか、何らかの値に置き換えるかを検討します。
また、ここで得られた知見を基に、次のステップとして「探索的分析(EDA)」を行うか、「前処理(クレンジング)」を行うかを決定します。
よく使われるグラフとして、以下のものがあります。。
| グラフ名 | 着眼点 | 概要 |
|---|---|---|
| ヒストグラム | 分布 | 分布の形状や偏り、山の数(モードの数)を確認するために使用します。 横軸にはデータの値(階級)、縦軸には度数(データの値が出現する回数)をプロットします。 |
| 箱ひげ図 | 分布 | データの散らばり具合や中央値、四分位数を確認するために使用します。 箱ひげ図はデータの統計情報を可視化するために用います。 |
| 時系列プロット | 周期性 | 時系列でパターンがあるかを確認するために使用します。 時刻データXと元データYで折れ線グラフを作成します。時刻データが無くても、データが時系列に沿って並んでいる場合は、Xを0~nの数値として代用します。 |
| QQプロット | 分布 | データがどれだけ正規分布に近いかを確認するために用います。 理論上の正規分布データXと元データYをそれぞれ小さい順に並べてプロットし、どれだけ直線に近いかで判定します。 |
| コレログラム | 周期性 | データの周期性を確認するために使用します。 時系列データの時刻 t における値Xと、Xから時間をずらした時刻(t + n)の値Yとの相関係数を計算し、縦軸に相関係数、横軸にずらした時間(ラグ)を用いて棒グラフで表します。 |
| ローレンツプロット | 周期性 | データの周期性やパターンを確認するために使用します。 時系列データの時刻 t における値Xと、t + 1 の値Yで散布図を作成します。パターンがなければ散布図は散乱しますが、明確な周期性があれば直線状に並びます。特定の状態が繰り返されている場合、1つまたは複数の点群ができます。単独の点が散らばる場合は外れ値と判断できます。この手法は元々心電図などの医学的分析で生まれたものであり、ローレンツ方程式とは無関係です。 |
コレログラムで周期性が見つかった場合は、次の方法を使ってどのような周期性があるかを確認します。
| スペクトル分析 (フーリエ変換) | 信号の周波数成分を分析する時に使用します。 フーリエ変換とも呼ばれており、信号に含まれる各周波数成分の強さや位相を分析することができます。フーリエ変換は音響や振動、画像、音声など様々な分野で活用されています。 |
|---|---|
| パワースペクトル | 信号のエネルギー量を可視化する時に使用します。 パワースペクトル密度プロットとも呼ばれており、フーリエ変換の結果を用いて、信号に含まれる各周波数成分のエネルギー量を可視化したものです。 |
| ローレンツプロット | 周期性のパターン(分布)を確認する時に使用します。 一般的には元データのN番目のデータと、N+1番目のデータを使って散布図を描いたものをローレンツプロットと呼びますが、コレログラムで周期性が見つかったときのYを用いることで、データの分布を確認することができます。 |
Python によるデータ探索(事前分析)のプログラム6例
統計情報の表示
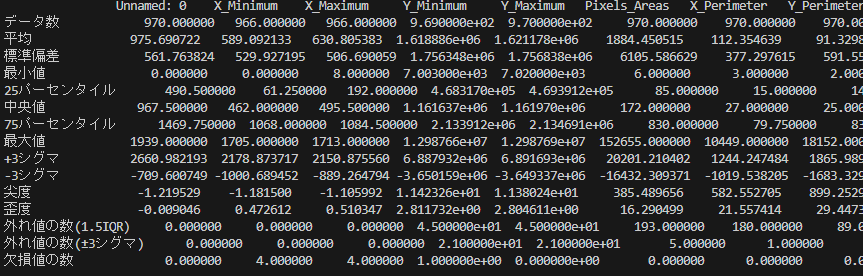
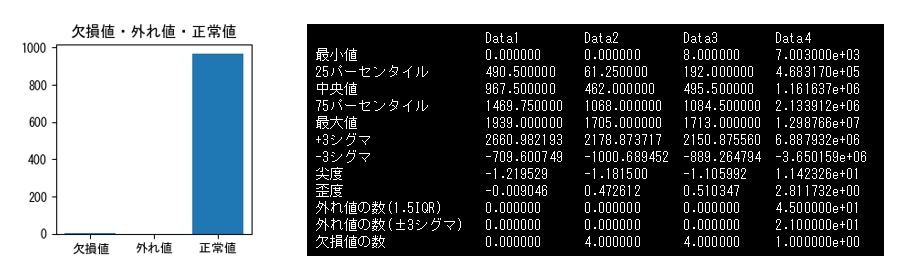
引数で指定したDataFrameから統計情報を計算し、DataFrameとして返すサンプルです。
import pandas as pd
import numpy as np
def summarize_data(df):
# 統計量を計算
statistics = df.describe(include="all")
# 外れ値の数、±3シグマの値、尖度、歪度を計算
outliers = {}
plus_3_sigma = {}
minus_3_sigma = {}
kurtosis_values = {}
skewness_values = {}
outliers_3sigma = {}
for col in df.select_dtypes(include=['int', 'float']).columns:
Q1 = statistics.loc['25%', col]
Q3 = statistics.loc['75%', col]
IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
outliers[col] = df[(df[col] < lower_bound) | (df[col] > upper_bound)].shape[0]
plus_3_sigma[col] = statistics.loc['mean', col] + 3 * statistics.loc['std', col]
minus_3_sigma[col] = statistics.loc['mean', col] - 3 * statistics.loc['std', col]
kurtosis_values[col] = df[col].kurtosis()
skewness_values[col] = df[col].skew()
# ±3シグマの範囲内での外れ値の数を計算
outliers_3sigma[col] = df[(df[col] < minus_3_sigma[col]) | (df[col] > plus_3_sigma[col])].shape[0]
# 欠損値の数を計算
missing_values = df.isnull().sum()
# 統計量に外れ値と欠損値の情報を追加
statistics.loc['+3sigma'] = plus_3_sigma
statistics.loc['-3sigma'] = minus_3_sigma
statistics.loc['kurtosis'] = kurtosis_values
statistics.loc['skewness'] = skewness_values
statistics.loc['outliers'] = outliers
statistics.loc['outliers_3sigma'] = outliers_3sigma
statistics.loc['missing_values'] = missing_values
# カラム名を日本語に変更
japanese_columns = {
'count': 'データ数',
'unique': 'ユニーク数',
'top': '最頻値',
'freq': '最頻値の出現回数',
'mean': '平均',
'std': '標準偏差',
'min': '最小値',
'25%': '25パーセンタイル',
'50%': '中央値',
'75%': '75パーセンタイル',
'max': '最大値',
'outliers': '外れ値の数(1.5IQR)',
'outliers_3sigma': '外れ値の数(±3シグマ)',
'missing_values': '欠損値の数',
'+3sigma': '+3シグマ',
'-3sigma': '-3シグマ',
'kurtosis': '尖度',
'skewness': '歪度'
}
return statistics.rename(index=japanese_columns)# データの読み込み
df = pd.read_csv("o:/sample.tsv", delimiter="\t")
# 統計量を取得
statistics = summarize_data(df)
print("統計量の一覧:")
print(statistics)データの可視化
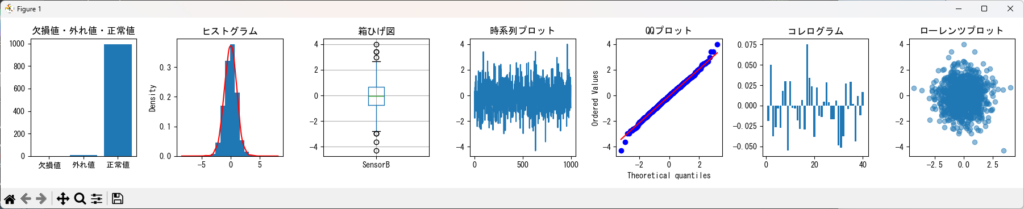
指定したDataFrameのカラムの値をグラフ化するサンプルです。データに含まれる欠損値・外れ値・正常値の棒グラフ、ヒストグラム、箱ひげ図、時系列プロット、QQプロット、コレログラムを描画できます。
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
# matplotlibに日本語フォントを設定
plt.rcParams['font.family'] = "MS Gothic"
def visualize_data(df, column_name):
"""
DataFrameとカラム名を受け取り、指定されたカラムのデータを視覚化する。
Parameters:
df (DataFrame): データフレーム
column_name (str): 視覚化したいカラムの名前
"""
# グラフのタイトルを日本語に設定
titles = ['欠損値・外れ値・正常値', 'ヒストグラム', '箱ひげ図', '時系列プロット', 'QQプロット', 'コレログラム','ローレンツプロット']
# グラフを横一列に並べる
fig, axes = plt.subplots(1, 7, figsize=(18, 3))
# 欠損値の数を計算
missing_values = df[column_name].isnull().sum()
# 外れ値の数を計算
Q1 = df[column_name].quantile(0.25)
Q3 = df[column_name].quantile(0.75)
IQR = Q3 - Q1
outlier_values = ((df[column_name] < (Q1 - 1.5 * IQR)) | (df[column_name] > (Q3 + 1.5 * IQR))).sum()
# 正常値の数を計算
total_values = len(df)
normal_values = total_values - missing_values - outlier_values
# 欠損値、外れ値、正常値の割合を積み上げグラフで表示
values = [missing_values, outlier_values, normal_values]
labels = ['欠損値', '外れ値', '正常値']
axes[0].bar(labels, values)
axes[0].set_title(titles[0])
# ヒストグラムとカーブ
df[column_name].plot(kind='hist', ax=axes[1], density=True)
df[column_name].plot(kind='kde', ax=axes[1], color='red')
axes[1].set_title(titles[1])
# 箱ひげ図
df.boxplot(column=column_name, ax=axes[2])
axes[2].set_title(titles[2])
# 時系列プロット
axes[3].plot(df.index, df[column_name])
axes[3].set_title(titles[3])
# QQプロット
stats.probplot(df[column_name].dropna(), dist="norm", plot=axes[4])
axes[4].set_title(titles[4])
# 過去40回の相関を計算
past_correlation = [df[column_name].autocorr(lag=i) for i in range(1, 41)]
# 相関の時間変化をプロット
axes[5].bar(range(1, 41), past_correlation)
axes[5].set_title(titles[5])
# 相関の時間変化をプロット
axes[6].scatter(df[column_name][:-1], df[column_name][1:], alpha=0.5)
axes[6].set_title(titles[6])
plt.tight_layout()
plt.show()# データの読み込み
df = pd.read_csv("o:/sample.tsv", delimiter="\t")
# データをグラフ化
visualize_data(df,df.columns[2])スペクトル分析(フーリエ変換)
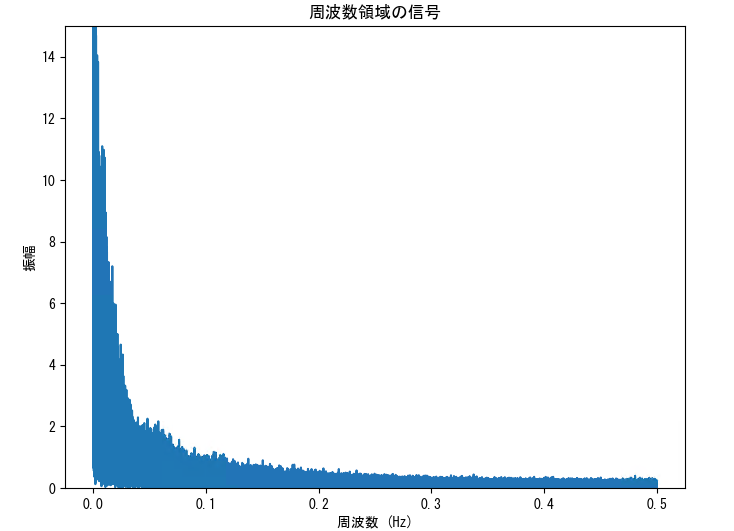
DataFrameの指定カラムにおいて、指定したサンプリング周波数(fs) でスペクトル分析(フーリエ変換)を行い、結果をグラフ化するサンプルです。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
def plot_frequency_domain_signal(dataframe, column_name, fs, xlim=None, ylim=None):
data = dataframe[column_name].values
N = len(data)
T = 1.0 / fs
yf = np.fft.fft(data)
xf = np.fft.fftfreq(N, T)[:N//2]
yf_magnitude = 2.0/N * np.abs(yf[:N//2])
plt.figure(figsize=(8, 6))
plt.plot(xf, yf_magnitude)
plt.title('周波数領域の信号')
plt.xlabel('周波数 (Hz)')
plt.ylabel('振幅')
if xlim:
plt.xlim(xlim)
if ylim:
plt.ylim(ylim)
plt.show()df = pd.read_csv("D:/CANデータ.csv",encoding="shift-jis")
# パワースペクトル密度プロットの作成
plot_frequency_domain_signal(df, '回転数', fs=1.0,ylim=(0,15)) # サンプリング周波数(fs)を1.0とする例パワースペクトル
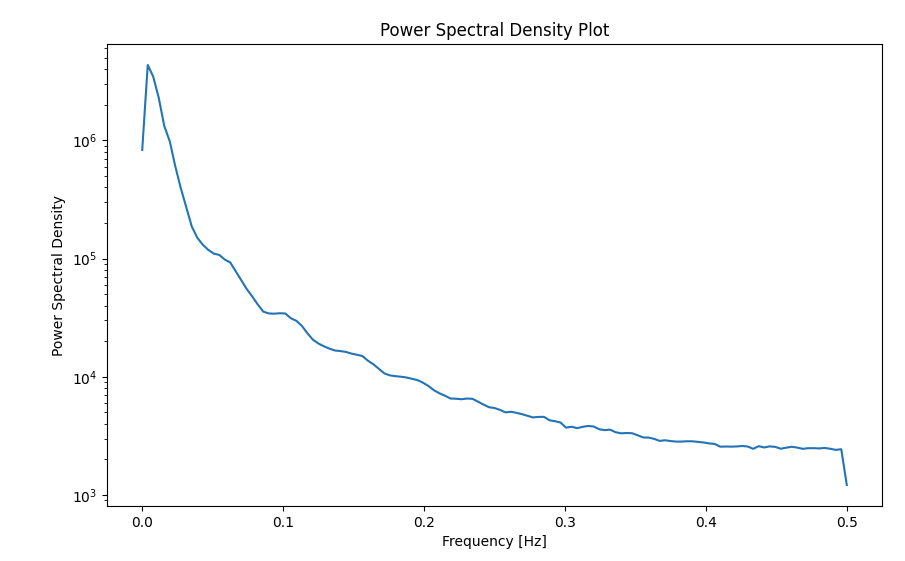
DataFrameの指定カラムにおいて、指定したサンプリング周波数(fs)でパワースペクトル密度プロットのグラフを作成するサンプルです。
import pandas as pd
import matplotlib.pyplot as plt
from scipy import signal
plt.rcParams['font.family'] = 'MS Gothic'
def plot_power_spectral_density(df, column_name, fs):
# サンプリング周波数(サンプリングレート)
f, Pxx = signal.welch(df[column_name], fs=fs)
# パワースペクトル密度プロットの作成
plt.figure(figsize=(10, 6))
plt.semilogy(f, Pxx)
plt.xlabel('Frequency [Hz]')
plt.ylabel('Power Spectral Density')
plt.title('Power Spectral Density Plot')
plt.show()df = pd.read_csv("o:/sample.tsv", delimiter="\t")
# パワースペクトル密度プロットの作成
plot_power_spectral_density(df, '回転数', fs=1.0) # サンプリング周波数を1.0とする例指定したカラム(複数)によるヒストグラム
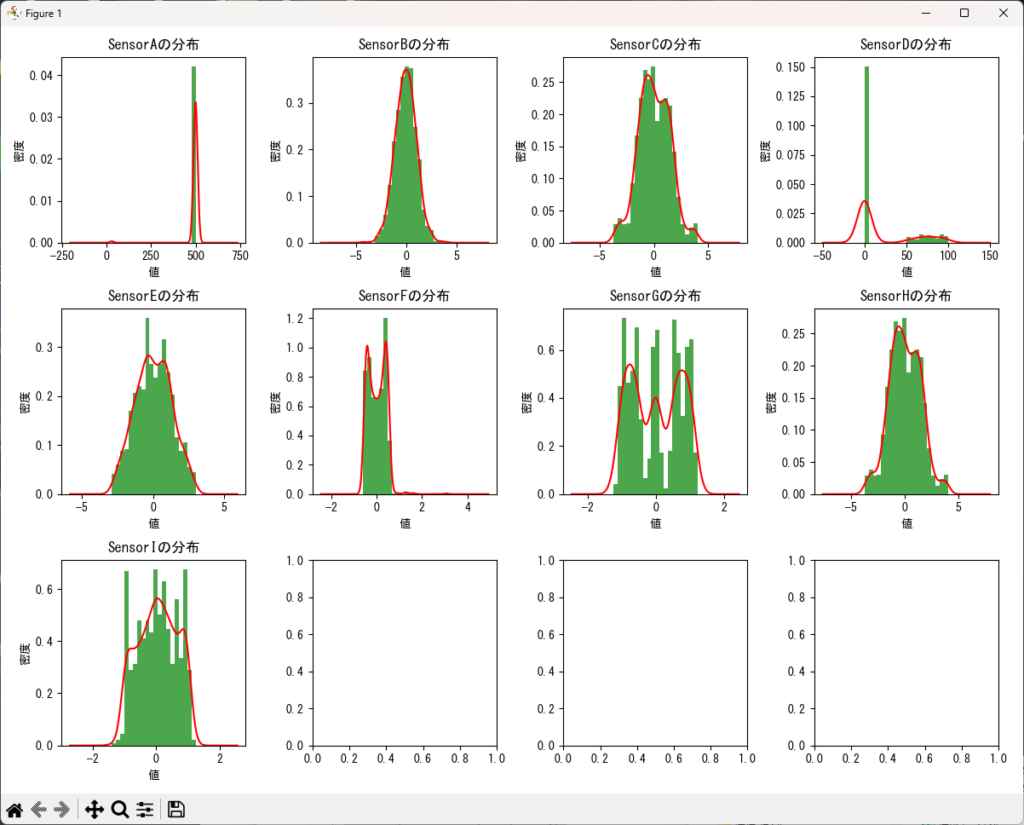
引数で渡されたDataFrameに対して、指定したカラムのリストに基づいてヒストグラムを作成するサンプルです。
import pandas as pd
import matplotlib.pyplot as plt
# matplotlibに日本語フォントを設定
plt.rcParams['font.family'] = "MS Gothic"
def distribution_plot(df, columns, graphs_per_row=2):
"""
指定された複数の列に対して、それぞれの列に対するヒストグラムと分布のカーブを横に並べて描画する関数。
Parameters:
df (DataFrame): データフレーム
columns (list): 描画する列の名前のリスト
graphs_per_row (int): 1行に並べるグラフの数(デフォルトは2)
"""
num_cols = len(columns)
num_rows = (num_cols + graphs_per_row - 1) // graphs_per_row
fig, axes = plt.subplots(num_rows, graphs_per_row, figsize=(graphs_per_row * 3, num_rows * 3))
for i, column in enumerate(columns):
row = i // graphs_per_row
col = i % graphs_per_row
ax = axes[row, col]
# 分布のヒストグラムを描画
ax.hist(df[column], bins=20, density=True, color='green', alpha=0.7)
df[column].plot(kind='kde', ax=ax, color='red')
ax.set_title(f"{column}の分布")
ax.set_xlabel("値")
ax.set_ylabel("密度")
plt.tight_layout()
plt.show()df = pd.read_csv("o:/AnomalyDetectionSample1.csv", delimiter=",")
# 関数を呼び出して分布のヒストグラムとカーブを描画
columns = df.columns[5:20] # 例として、最初の4列に対して分布のヒストグラムを描画
distribution_plot(df, columns, graphs_per_row=5)指定したカラム(複数)によるコレログラム
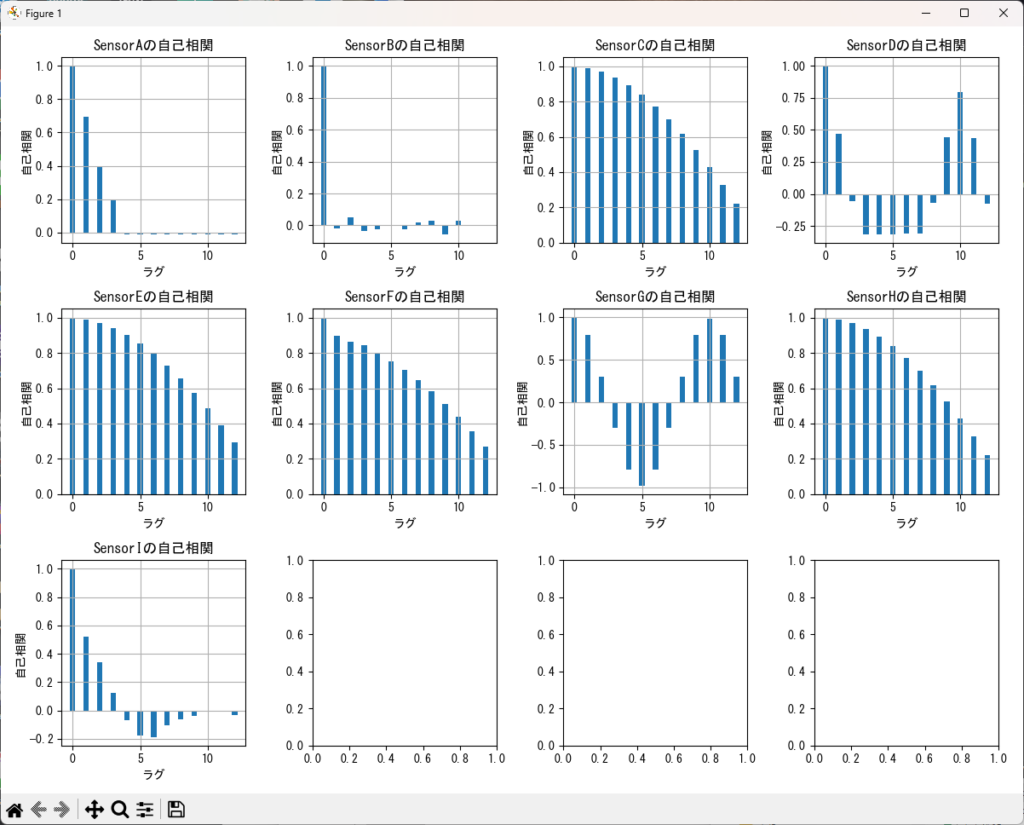
引数で渡されたDataFrameに対して、指定したカラムのリストに基づいてコレログラムを作成するサンプルです。
import pandas as pd
import matplotlib.pyplot as plt
# matplotlibに日本語フォントを設定
plt.rcParams['font.family'] = "MS Gothic"
def autocorrelation_plot(df, columns, max_lag, dot_size=20, graphs_per_row=3):
"""
指定された複数の列に対して、それぞれの列に対する自己相関の棒グラフを横に並べて描画する関数。
Parameters:
df (DataFrame): データフレーム
columns (list): 描画する列の名前のリスト
max_lag (int): 自己相関を計算するための最大の過去の個数
graphs_per_row (int): 1行に並べるグラフの数(デフォルトは3)
"""
num_cols = len(columns)
num_rows = (num_cols + graphs_per_row - 1) // graphs_per_row
fig, axes = plt.subplots(num_rows, graphs_per_row, figsize=(graphs_per_row * 3, num_rows * 3))
for i, column in enumerate(columns):
row = i // graphs_per_row
col = i % graphs_per_row
ax = axes[row, col]
lags = range(max_lag + 1)
autocorrs = [df[column].autocorr(lag=lag) for lag in lags]
ax.bar(lags, autocorrs, width=0.4)
ax.set_title(f"{column}の自己相関")
ax.set_xlabel("ラグ")
ax.set_ylabel("自己相関")
ax.grid(True)
plt.tight_layout()
plt.show()df = pd.read_csv("o:/AnomalyDetectionSample1.csv", delimiter=",")
max_lag = 12 # 自己相関を計算するための最大の過去の個数
autocorrelation_plot(df, df.columns, max_lag, graphs_per_row=4)指定したカラム(複数)によるローレンツプロット
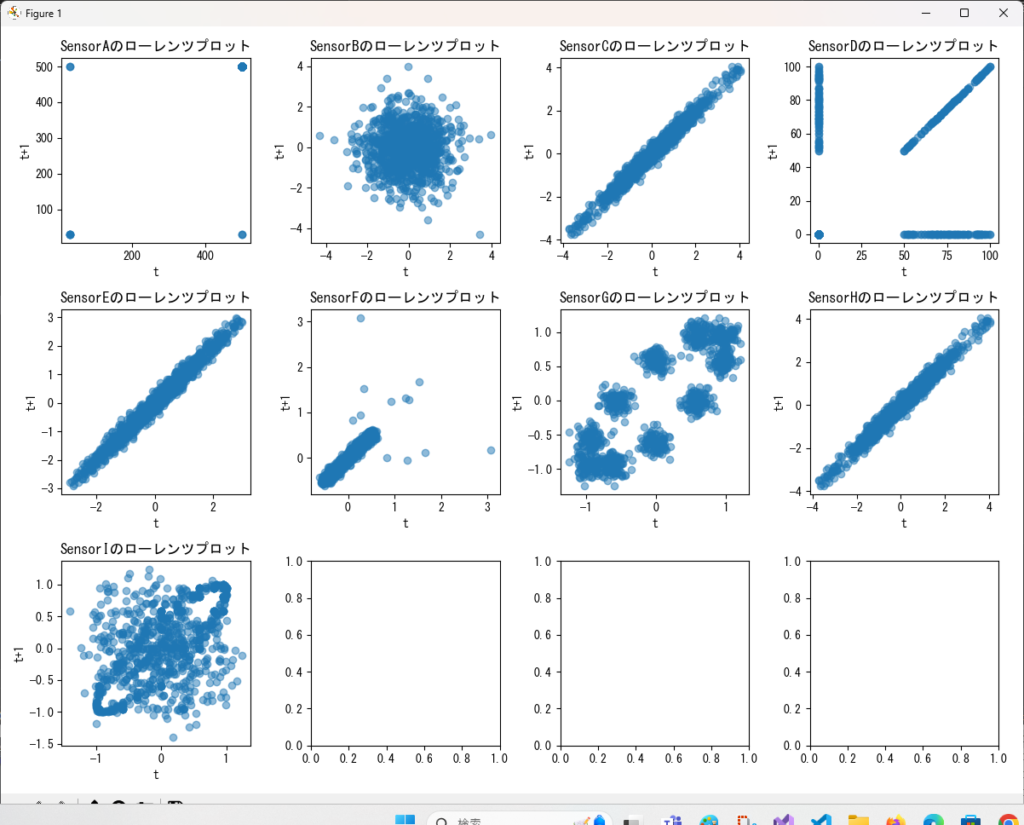
引数で渡されたDataFrameに対して、指定したカラムのリストに基づいてローレンツプロットを作成するサンプルです。
import pandas as pd
import matplotlib.pyplot as plt
# matplotlibに日本語フォントを設定
plt.rcParams['font.family'] = "MS Gothic"
def lorentz_plot(df, columns, graphs_per_row=2):
"""
指定された複数の列に対して、それぞれの列に対するヒストグラムと分布のカーブを横に並べて描画する関数。
Parameters:
df (DataFrame): データフレーム
columns (list): 描画する列の名前のリスト
graphs_per_row (int): 1行に並べるグラフの数(デフォルトは2)
"""
num_cols = len(columns)
num_rows = (num_cols + graphs_per_row - 1) // graphs_per_row
fig, axes = plt.subplots(num_rows, graphs_per_row, figsize=(graphs_per_row * 3, num_rows * 3))
for i, column in enumerate(columns):
row = i // graphs_per_row
col = i % graphs_per_row
ax = axes[row, col]
# 分布のヒストグラムを描画
ax.scatter(df[column][:-1], df[column][1:], alpha=0.5)
ax.set_title(f"{column}のローレンツプロット")
ax.set_xlabel("t")
ax.set_ylabel("t+1")
plt.tight_layout()
plt.show() # データの読み込み
df = pd.read_csv("p:/CSV/AnomalyDetectionSample1.csv", delimiter=",")
# データをグラフ化
lorentz_plot(df,df.columns,graphs_per_row=4)まとめ
今回の記事では、データの理解と分析の手順について詳しく説明しました。
データ探索(事前分析)は、データ自体を理解することです。
そのための手順として、次の項目について詳しく解説しました。
- データの発生元、信頼性の確認
- データ形式の確認
- データ項目の確認
- データの欠損値や異常値の確認
- データの分布や傾向を確認する
また、データの欠損値や異常、分布や傾向を把握するための方法として、pythonのサンプルコードをいくつか紹介しました。
- 統計情報の表示
- データの可視化(ヒストグラム、箱ひげ図、時系列プロット、QQプロット、コレログラムなど)
- 指定したカラムによるヒストグラム
- 指定したカラムによるコレログラム








コメント