本記事は「【成功の秘訣】現場で使えるデータ分析手順を体系的に解説」で紹介した探索的分析(EDA)の具体的な手順と、EDAで良く用いられる分析手法のPythonサンプルコードを紹介しています。
探索的データ分析(EDA)の目的

探索的分析(EDA=Exploratory data analysis)は、データの特徴、構造、異常値などを体系的に分析することで、そこから仮説を導き出し、それに基づいて分析方針を選定するための活動です。具体的には、統計分析、機械学習、データ可視化などの手法を組み合わせ、データに潜むルールや規則性を浮き彫りにします。
探索的分析は、前段階の「【成功の秘訣】データ探索(事前分析)の手順と方法を解説(Pythonソースコード付き)」で得られた知見をベースに、次の作業を行います。
- データの統計量を確認する
- データの傾向や分布を確認する
- 欠損値や異常値の処理方法を検討する
- 変数間の関係性を確認する
- データが待つパターンを分析する
- 仮説を立て、分析方針を選定する
探索的データ分析(EDA)の手順

データの統計量を確認する

データの統計量をグラフ化することにより、データがどのように変化しているのか、それが線形なのか非線形なのか、分布が正規分布に従っているのか、偏りや裾野の状態はどうなっているのか、欠損値、異常値がどの程度含まれているのかを確認します。
ここでのポイントは、データの品質を評価し、分析に足る品質にするための前処理(欠損値・異常値処理を含む)の必要性を検討することです。
分析対象件数が十分に多く、欠損値が極めて少ない場合は、無条件に欠損値のある行を削除するという方法も選択できますが、欠損値が多い場合は何らかの補完が必要かもしれません。
異常値が見つかった場合でも、それは単なるノイズなのか、あるいは分析する上で必要な情報かのかを見極めなければなりません。
欠損値や異常値の判断にはドメイン知識が必要になるため、有識者と相談できるように結果をまとめておきます。
正規分布になっているか否かで使える分析手法が異なってきますが、提供されるデータが理想的な正規分布であることは稀であるため、多少崩れているだけなら正規分布と断定してしまうことも多いです。
データのトレンドを確認する

データにトレンド(長期的な増減傾向)や季節性(一定期間ごとの繰り返しパターン)が存在する場合、それを把握しておかないと、誤った分析を行うリスクが生じます。
- 微細な変動の隠蔽:
センサーデータの微細な変動などを分析したい場合、往々にしてトレンドは短期的な変動を覆い隠してしまいます。トレンドを除去することで、よりクリアに短期的なパターンや異常値を捉えることができます。 - 非定常化データの分析:
多くの時系列分析モデルは、データが時間を通じて統計的な性質(平均や分散)が一定である(定常性を持つ)ことが前提としています。トレンドはデータの平均や分散を時間とともに変化させる(非定常性)ため、そのままでは正しい分析ができません。差分法などでトレンドを除去し、データを定常化させる必要があります。 - 異なるデータの比較:
全体的に増加傾向にある複数のセンサーデータを比較する際に、個々のトレンドが異なると、相互の関連性が見えにくくなることがあります。トレンドを除去することで、共通の短期的な変動パターンや相互の影響をより明確に分析できます。 - 見せかけの相関:
全く関係のない2つの時系列データが、偶然にも似たようなトレンドを示すことがあります。この場合、実際には因果関係がないのに相関があるように見えてしまいます。トレンドを除去することで、このような見せかけの相関を排除し、より信頼性の高い関係性を分析することができます。 - 特定の基準からの逸脱度:
ある目標値に対して、実際のデータが長期的に乖離していく傾向(トレンド)がある場合、そのトレンドを除去することで、短期的な目標達成度や逸脱の度合いをより正確に評価できます。
トレンドを可視化する方法として、1つ前の値との差(階差)や、移動平均と元データの差をグラフ化することがよく行われます。また、累積和(1つ前の値との和)をグラフ化することで、トレンドの増減傾向(増減幅は一定なのか、変化があるのか)が把握できます。
損値や異常値の処理方法を検討する
欠損値と異常値が存在する場合、ここまでの分析でまとめた情報(欠損値や異常値の件数、欠損値や異常値の処置案)を有識者と相談し、最終的な処置方法を決定します。
欠損値が無視できるほど少ない場合、欠損値のある行を削除することが一つの選択肢となります。しかし、欠損値が多い場合は、何らかの補完方法を検討しなければなりません。
異常値についても件数が少なければ除外することで対応可能ですが、無視できない場合は妥当な値に置き換える、正しい値に修正するなどの処置方法を検討します。
変数間の関係性を分析する
相関分析や回帰分析などの統計手法を用いて、変数間の関係性を分析します。
相関分析は、変数間の相関係数を計算し、二つの変数がどの程度関連しているかを数値化する手法です。一方、回帰分析は、一つの変数に対して、どの変数がどれくらい影響しているかを探る手法です。これらの手法を駆使することで、変数間の影響や相互作用を明確にすることが可能です。
ただし、時系列データを扱う際には特に注意が必要です。たとえ本来無関係な変数であっても、ランダムウォークのような非定常な性質を持つ場合、見かけ上高い相関関係が示されたり、統計的に有意な回帰結果が得られたりすることがあります。これは「見かけ上の回帰」と呼ばれる現象であり、誤った結論を導く可能性があります。
このため、時系列データの変数間の関係性を分析する際には、データの定常性の確認、差分系列の利用、共和分分析などの適切な手法を検討することが重要です。また、統計的な結果だけでなく、ドメイン知識に基づいてその関係性の妥当性を慎重に評価する必要があります。
データが待つパターンを分析する
どのような分析手法が適しているかの判断材料の1つとして、データが持つパターンを分析します。ここでは、データのクラスタリングや次元削減の手法がよく用いられます。
手法1.クラスタリング
クラスタリングは、データを類似した特徴を持つグループ(クラスタ)に分割する手法です。クラスタリングは教師なし学習の一種であり、データの内部構造に基づいて自然なグループに分類します。代表的なクラスタリング手法には、k-means法や階層的クラスタリングなどがあります。
| k-means法 | k-means法は、データをあらかじめ指定された数のクラスタ(k)に分割する方法です。各クラスタの中心点をランダムに選び、各データ点を最も近い中心点に割り当てます。このプロセスを繰り返し、クラスタの中心点を更新していきます。最終的には、クラスタ内のデータ点の距離の合計が最小になるようにクラスタリングされます。 |
|---|---|
| 階層的クラスタリング | 階層的クラスタリングは、データポイントを階層的な構造でクラスタに分ける方法です。この手法には、凝集型(bottom-up)と分割型(top-down)の2つのアプローチがあります。凝集型は、まずすべてのデータポイントを個別のクラスタとして扱い、類似度が高いクラスタを統合していきます。一方、分割型は、すべてのデータポイントを1つのクラスタとして扱い、類似度が低いクラスタを分割していきます。 |
| DBSCAN | DBSCAN(Density-Based Spatial Clustering of Applications with Noise)は、密度に基づいてクラスタを形成する方法です。データポイントの密度が高い領域はクラスタとして認識され、密度が低い領域はノイズとして扱われます。DBSCANは、クラスタの数を事前に指定する必要がないため、柔軟性が高いとされています。 |
手法2.次元削減
次元削減は、高次元のデータを低次元のデータに変換する手法です。高次元のデータでは、データの可視化や解釈が困難であったり、計算コストが高くなる傾向があります。次元削減は、データの持つ重要な情報を保持しつつ、データの次元を削減し、データの解釈や処理の効率化を図ります。代表的な次元削減手法には、主成分分析(PCA)、t-SNE、UMAPなどがあります。
| 主成分分析(PCA) | 主成分分析は、データの持つ情報を保持しつつ、データを直交する新しい軸(主成分)に変換する手法です。データの分散が最大となるような軸を見つけ出し、その軸に射影することで次元を削減します。主成分分析は線形変換を行うため、線形な構造を持つデータに適しています。 |
|---|---|
| t-SNE | t-SNE(t-distributed Stochastic Neighbor Embedding)は、データの局所的な関係性をできるだけ保持しつつ、データを低次元空間に埋め込む手法です。t-SNEでは、高次元空間でのデータポイント間の類似度を低次元空間での類似度に反映するようなマップを学習します。t-SNEは非線形な関係を捉えることができるため、可視化に適しています。 |
| UMAP | UMAP(Uniform Manifold Approximation and Projection)は、高次元データを低次元空間に埋め込む手法です。t-SNEに似ていますが、より高速かつ大規模なデータセットにも適用可能です。UMAPは局所的な構造を保持しつつ、グローバルな構造をより正確に捉えることができるとされています。 |
主成分分析の結果(主成分が持つ意味や寄与度)をドメイン知識に基づいて解釈することで、新しい指標の発見やデータ分類のためのヒントとして利用できます。しかし、これは本格的な分析において必要に応じて行われるべきものです。探索的データ分析(EDA)の段階では、主成分分析はあくまでも次元削減の手段として用いることが多いです。
仮説を立て、分析方針を選定する
データの探索や事前分析の後に、探索的データ解析(EDA)を実施することで、設定した分析方針の妥当性がより鮮明になったと思います。
新しい発見や気づきがあれば、それに基づいて有益な仮説を立て、アプローチ方法や分析方針を再検討することで、分析結果の精度向上や作業効率の向上が期待できます。
ただし、誤った仮説は逆効果になる可能性があるため、ドメイン知識を持つ有識者に仮説の正当性を確認するか、有識者と結果を共有し、ディスカッションを通じて仮説を立てることが重要です。
Python による探索的データ分析(EDA)のプログラム7例
統計量の確認グラフの描画

引数で指定されたDataFrameに対して、指定したカラムの統計情報とグラフを作成するサンプルです。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
# matplotlibに日本語フォントを設定
plt.rcParams['font.family'] = "MS Gothic"
def plot_data_insights(df, column_name, std_threshold=3, title=None):
"""
DataFrameの指定したカラムの統計量を可視化する複数のグラフを横一列に描画する。
Args:
df (pd.DataFrame): 入力DataFrame。
column_name (str): グラフを描画するカラム名。
std_threshold (float, optional): 外れ値を検出する際の標準偏差の閾値。デフォルトは3。
title (str, optional): グラフのタイトル。デフォルトはNone。
"""
data_col = df[column_name]
valid_data = data_col.dropna()
n_total = len(data_col)
n_missing = data_col.isnull().sum()
mean = valid_data.mean()
std = valid_data.std()
upper_threshold = mean + std_threshold * std
lower_threshold = mean - std_threshold * std
outliers = valid_data[(valid_data > upper_threshold) | (valid_data < lower_threshold)]
n_outliers = len(outliers)
normal_values = valid_data[(valid_data <= upper_threshold) & (valid_data >= lower_threshold)]
n_normal = len(normal_values)
prop_normal = (n_normal / n_total) * 100 if n_total > 0 else 0
prop_outliers = (n_outliers / n_total) * 100 if n_total > 0 else 0
prop_missing = (n_missing / n_total) * 100 if n_total > 0 else 0
median_normal = normal_values.median() if not normal_values.empty else np.nan
mean_normal = normal_values.mean() if not normal_values.empty else np.nan
std_normal = normal_values.std() if not normal_values.empty else np.nan
min_normal = normal_values.min() if not normal_values.empty else np.nan
max_normal = normal_values.max() if not normal_values.empty else np.nan
variance_normal = normal_values.var() if not normal_values.empty else np.nan
fig, axes = plt.subplots(1, 5, figsize=(25, 5))
fig.suptitle(f'{title if title else column_name} の統計グラフ')
# 棒グラフ (一番左)
labels = ['欠損値', '外れ値', '正常値']
counts = [n_missing, n_outliers, n_normal]
bar_colors = ['skyblue', 'salmon', 'lightgreen']
bars = axes[0].bar(labels, counts, color=bar_colors) # labelを削除
axes[0].set_title(f'データ内訳')
axes[0].set_ylim(0, max(counts) * 1.2) # y軸の範囲を調整
# 凡例に表示するテキストを作成
legend_text = (f'総件数: {n_total}件\n'
f'正常値: {n_normal}件 ({prop_normal:.1f}%)\n'
f'外れ値: {n_outliers}件 ({prop_outliers:.1f}%)\n'
f'欠損値: {n_missing}件 ({prop_missing:.1f}%)\n'
f'\n正常値統計量:\n'
f'平均: {mean_normal:.2f}\n'
f'中央値: {median_normal:.2f}\n'
f'標準偏差: {std_normal:.2f}\n'
f'分散: {variance_normal:.2f}\n'
f'最小: {min_normal:.2f}\n'
f'最大: {max_normal:.2f}\n'
f'外れ値閾値 (±{std_threshold}σ):\n'
f'[{lower_threshold:.2f}, {upper_threshold:.2f}]')
axes[0].legend([legend_text], loc='upper left', fontsize=10, frameon=False) # frameon=Falseで枠線をなくす
# 箱ひげ図 (左から2番目)
sns.boxplot(y=valid_data, ax=axes[1])
axes[1].set_title('箱ひげ図')
# ヒストグラム
sns.histplot(valid_data, kde=True, ax=axes[2])
axes[2].set_title('ヒストグラム')
# バイオリンプロット
sns.violinplot(y=valid_data, ax=axes[3])
axes[3].set_title('バイオリンプロット')
# QQプロット
stats.probplot(valid_data, plot=axes[4])
axes[4].set_title('QQプロット')
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()
# データの読み込み
df = pd.read_csv(f"P:\sample\Csv\csv\Sample1.csv", delimiter=",")
# データをグラフ化
plot_data_insights(df,df.columns[1])df = pd.read_csv("o:/sample.tsv", delimiter="\t")
# 関数を呼び出してグラフを表示
plot_data_insights(df,df.columns[1])トレンドを可視化するグラフの描画

引数で指定されたDataFrameに対して、指定したカラムにおけるトレンドを把握するためのグラフを描画するサンプルです。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# matplotlibに日本語フォントを設定
plt.rcParams['font.family'] = "MS Gothic"
def plot_trend_removal_single_col_with_cumulative(df, column_name, window=5):
"""
単一のカラムの値を使い、トレンドを除外したグラフと累積和のグラフを横に4つ並べて描画する。
- 元の値と移動平均のグラフ
- 階差のグラフ
- 元の値 - 移動平均 のグラフ
- 累積和のグラフ
Args:
df (pd.DataFrame): 入力DataFrame。
column_name (str): グラフを描画するカラム名。
window (int, optional): 移動平均の窓幅(個数)。デフォルトは5。
"""
if column_name not in df.columns:
raise ValueError(f"指定されたカラム '{column_name}' はDataFrameに存在しません。")
data = df[column_name].dropna().reset_index(drop=True) # indexをリセットして0からの連番にする
rolling_mean = data.rolling(window=window).mean().dropna().reset_index(drop=True)
diff_series = data.diff().dropna().reset_index(drop=True)
detrended_ma = data.iloc[rolling_mean.index] - rolling_mean
cumulative_sum = data.cumsum()
fig, axes = plt.subplots(1, 4, figsize=(25, 5))
fig.suptitle(f'{column_name} のトレンド除去と累積和', fontsize=16)
# 1 元データと移動平均のグラフ
axes[0].plot(data, label='元の値', alpha=0.6)
axes[0].plot(rolling_mean, label=f'移動平均 (窓幅 {window})', color='red')
axes[0].set_title(f'元の値と移動平均 (窓幅 {window})')
axes[0].set_xlabel('データ順')
axes[0].set_ylabel('値')
axes[0].legend()
axes[0].grid(True)
# 2. 階差のグラフ
axes[1].plot(diff_series, label='階差')
axes[1].set_title('階差')
axes[1].set_xlabel('データ順')
axes[1].set_ylabel('階差')
axes[1].legend()
axes[1].grid(True)
# 3. 元の値 - 移動平均 のグラフ
axes[2].plot(detrended_ma, label=f'元の値 - 移動平均 (窓幅 {window})')
axes[2].set_title(f'トレンド除去 (元の値 - 移動平均、窓幅 {window})')
axes[2].set_xlabel('データ順')
axes[2].set_ylabel('トレンド除去後の値')
axes[2].legend()
axes[2].grid(True)
# 4. 累積和のグラフ
axes[3].plot(cumulative_sum, label='累積和', color='green')
axes[3].set_title('累積和')
axes[3].set_xlabel('データ順')
axes[3].set_ylabel('累積値')
axes[3].legend()
axes[3].grid(True)
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()# サンプルデータの作成
data = np.linspace(10, 30, 100) + np.random.randn(100) * 2 + np.sin(np.linspace(0, 10 * np.pi, 100)) * 5
df_sample = pd.DataFrame({'Value': data})
# 関数の実行 (累積和を含むバージョン)
plot_trend_removal_single_col_with_cumulative(df_sample, 'Value', window=7)総当たりによる散布図の描画
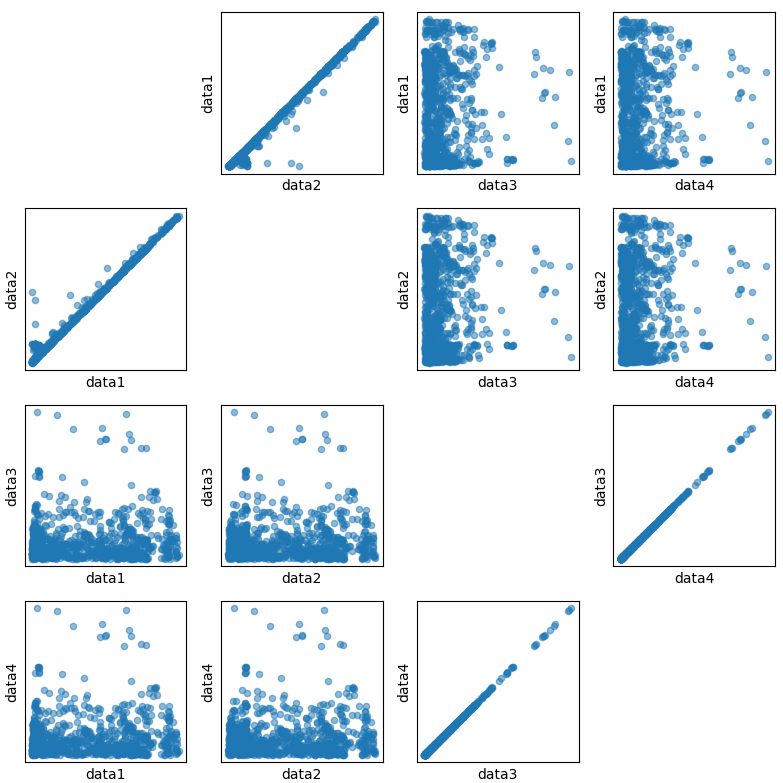
引数で指定されたDataFrameに対して、指定したカラムのリストから総当たりで散布図を作成するサンプルです。
import pandas as pd
import matplotlib.pyplot as plt
import itertools
# matplotlibに日本語フォントを設定
plt.rcParams['font.family'] = "MS Gothic"
def scatter_matrix(df, columns, dot_size=20):
"""
指定された列の総当たりの散布図を1枚のグラフに描画する関数。
Parameters:
df (DataFrame): データフレーム
columns (list): 描画する列のリスト
dot_size (int): ドットのサイズ(デフォルトは20)
"""
# グラフのサイズを設定
num_cols = len(columns)
fig, axes = plt.subplots(num_cols, num_cols, figsize=(8, 8))
# 散布図を描画
for i, j in itertools.product(range(num_cols), range(num_cols)):
if i != j:
ax = df.plot.scatter(x=columns[j], y=columns[i], ax=axes[i, j], alpha=0.5, s=dot_size)
ax.tick_params(axis='both', which='both', bottom=False, left=False, labelbottom=False, labelleft=False)
ax.set_xlabel(columns[j])
ax.set_ylabel(columns[i])
else:
axes[i, j].axis('off') # 対角線上のグラフは非表示にする
plt.tight_layout()
plt.show()df = pd.read_csv("o:/sample.tsv", delimiter="\t")
# 関数を呼び出して散布図を表示
columns = df.columns[1:5]
scatter_matrix(df,columns)
総当たりによる相関係数ヒートマップの描画
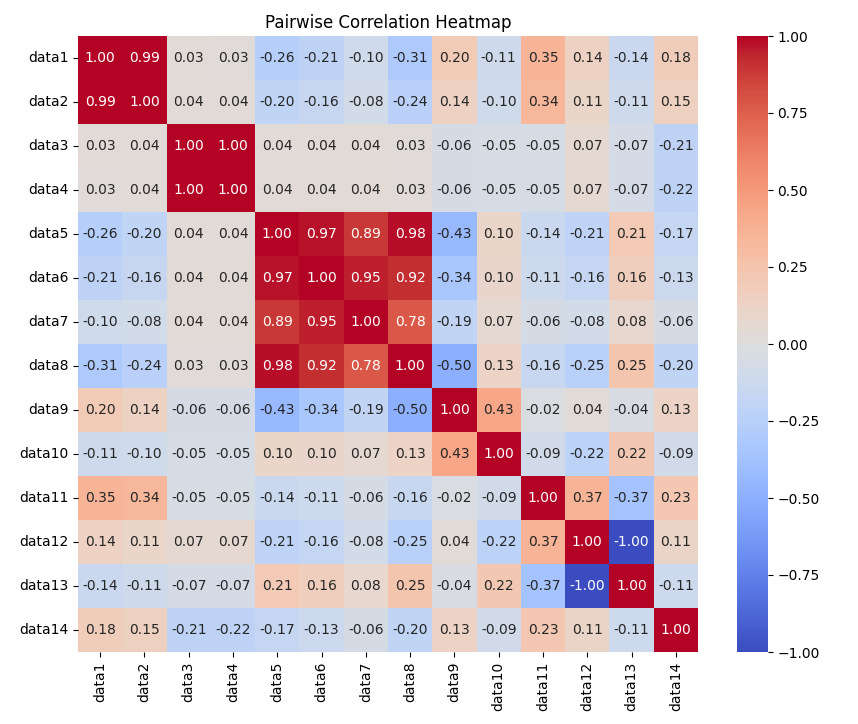
引数で指定されたDataFrameに対して、指定されたカラムを総当たりで相関係数を計算し、ヒートマップとして可視化するサンプルです。カラム数が多い場合はこちらの方が見やすいです。
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import itertools
# matplotlibに日本語フォントを設定
plt.rcParams['font.family'] = "MS Gothic"
def heatmap_matrix(df, columns):
"""
指定された列の総当たりの相関行列をヒートマップとして表示する関数。
Parameters:
df (DataFrame): データフレーム
columns (list): 描画する列のリスト
"""
# 指定された列の相関行列を計算
correlation_matrix = df[columns].corr()
# ヒートマップを作成
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, cmap='coolwarm', annot=True, fmt='.2f', vmin=-1, vmax=1)
plt.title('Pairwise Correlation Heatmap')
plt.show()
# 利用例
df = pd.read_csv("o:/sample.tsv", delimiter="\t")
# 関数を呼び出して散布図を表示
columns = df.columns[1:15]
heatmap_matrix(df,columns)
指定したラグの散布図の描画
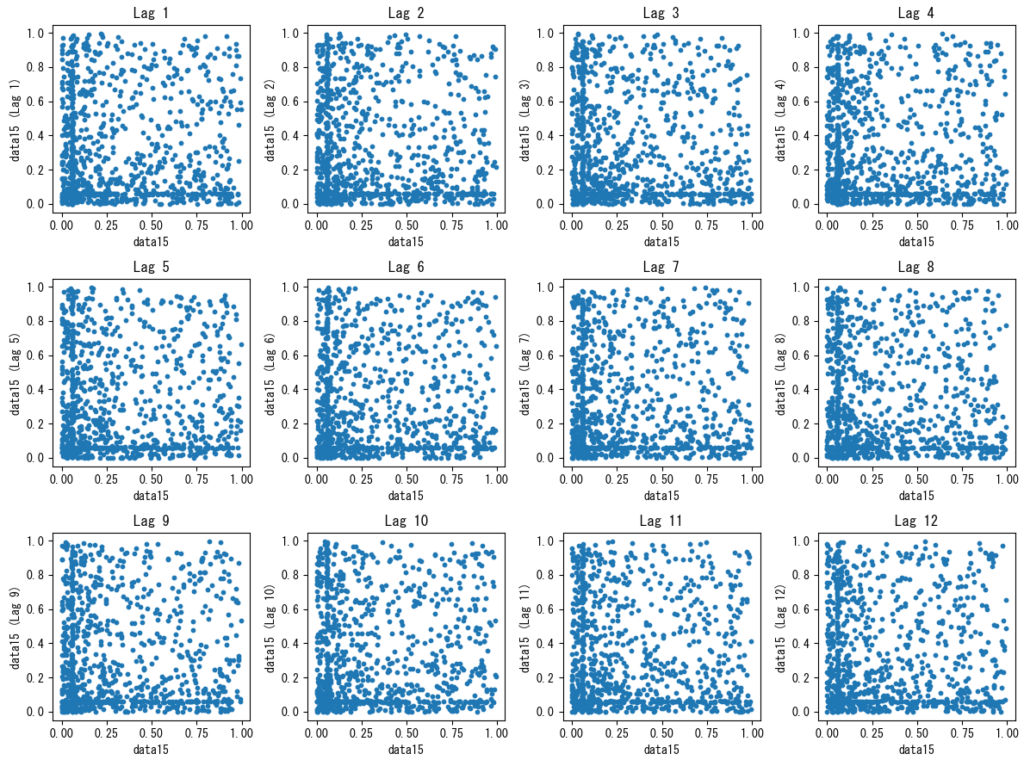
引数で指定されたDataFrameのカラムに対して、指定したラグのリストで散布図を作成します。コレログラムで高い相関が確認された場合、そのラグを可視化することで、データの散らばり具合や外れ値の有無、パターンの発見などに役立ちます。
import pandas as pd
import matplotlib.pyplot as plt
import itertools
# matplotlibに日本語フォントを設定
plt.rcParams['font.family'] = "MS Gothic"
def autocorrelation_plot(df, column, lags, dot_size=20, graphs_per_row=3):
"""
指定された列に対して、指定されたラグの自己相関の散布図を横に並べて描画する関数。
Parameters:
df (DataFrame): データフレーム
column (str): 描画する列の名前
lags (list of int): ラグのリスト
dot_size (int): ドットのサイズ(デフォルトは20)
graphs_per_row (int): 1行に並べるグラフの数(デフォルトは3)
"""
num_lags = len(lags)
num_rows = (num_lags + graphs_per_row - 1) // graphs_per_row
fig, axes = plt.subplots(num_rows, graphs_per_row, figsize=(graphs_per_row * 3, num_rows * 3))
for i, lag in enumerate(lags):
row = i // graphs_per_row
col = i % graphs_per_row
ax = axes[row, col]
x = df[column]
y = df[column].shift(-lag)
ax.scatter(x, y, s=dot_size)
ax.set_title(f"Lag {lag}")
ax.set_xlabel(column)
ax.set_ylabel(f"{column} (Lag {lag})")
plt.tight_layout()
plt.show()df = pd.read_csv("o:/sample.tsv", delimiter="\t")
# 関数を呼び出して自己相関のグラフを横に並べて表示
column = df.columns[15]
lags = [1, 2, 3, 4, 5, 6,7,8,9,10,11,12] # 例として、ラグ1から12までの自己相関を表示
autocorrelation_plot(df, column, lags, dot_size=10, graphs_per_row=4)クラスタリング
0:['data6', 'data7', 'data9', 'data10', 'data12', 'data13', 'data14', 'data15', 'data16', 'data17', 'Outside_X_Index', 'data18', 'data19', 'data20', 'data21', 'data22', 'data23', 'data24', 'data25', 'data26', 'data27']
1:['data3', 'data4']
2:['data8']
3:['data5']
4:['daga0', 'data1', 'data2', 'data11']
引数で指定されたDataFrameに対して、Kで指定した個数でクラスタリングを実施し、分類結果を辞書で返します。
import pandas as pd
from sklearn.cluster import KMeans
def clustering_with_labels(df, K):
"""
指定されたデータフレームを指定された数のクラスタにクラスタリングし、各クラスタのクラスタリングされたカラム名とクラスタ番号を含む辞書を返す関数。
Parameters:
df (DataFrame): クラスタリングするデータフレーム
K (int): クラスタの数
Returns:
clusters (dict): 各クラスタのクラスタリングされたカラム名とクラスタ番号を含む辞書
"""
# NaN値を含む行を削除
df.dropna(inplace=True)
# データフレームを転置してクラスタリングを実行
kmeans = KMeans(n_clusters=K)
kmeans.fit(df.T)
# 各データポイントのクラスタラベルを取得
labels = kmeans.labels_
# クラスタごとにクラスタリングされたカラム名のリストを作成し、辞書に格納
clusters = {}
for cluster_id in range(K):
cluster_data = df.columns[labels == cluster_id].tolist()
clusters[cluster_id] = cluster_data
return clustersdf = pd.read_csv("o:/sample.tsv", delimiter="\t")
# クラスタリングを実施
clusters = clustering_with_labels(df, 5)
#結果を表示
for key,val in clusters.items() :
print(f"{key}:{val}")クラスタリングが簡単に行える便利な自作クラスを「【製造業】データ分類と異常検知の強い味方!クラスタリングとは?」に掲載しています。併せてご覧ください。
主成分分析
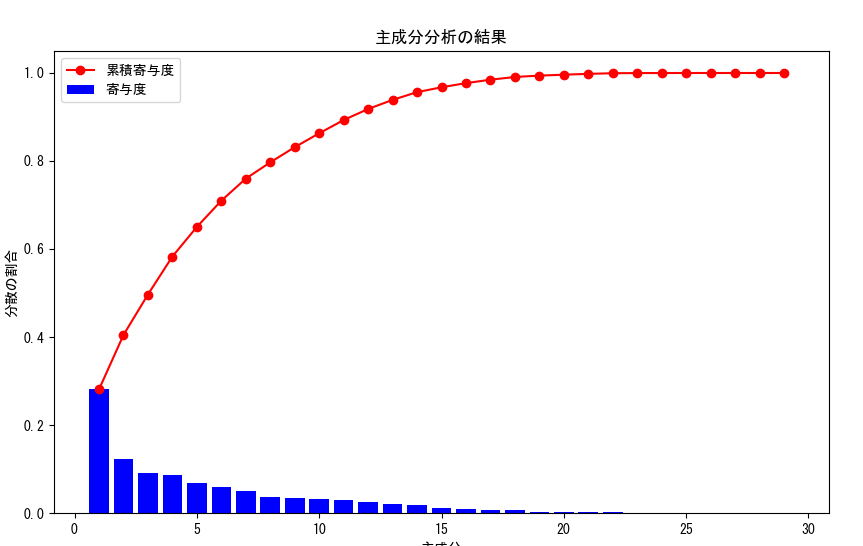
引数で指定されたDataFrameに対して、主成分分析を実施します。
import pandas as pd
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
# matplotlibに日本語フォントを設定
plt.rcParams['font.family'] = "MS Gothic"
def apply_pca(df):
"""
主成分分析を実行して、寄与度と累積寄与度を可視化する関数。
Parameters:
df (DataFrame): データフレーム
Returns:
pca (PCA): 主成分分析のモデル
"""
# 欠損値を含む行を削除する
df.dropna(inplace=True)
# データの標準化
scaled_data = (df - df.mean()) / df.std()
# 主成分分析(n_componentsで求める主成分の数を指定)
pca = PCA(n_components=None)
pca.fit(scaled_data)
# 寄与度と累積寄与度を取得
explained_variance_ratio = pca.explained_variance_ratio_
cumulative_explained_variance_ratio = explained_variance_ratio.cumsum()
# 寄与度と累積寄与度を可視化
plt.figure(figsize=(10, 6))
plt.bar(range(1, len(explained_variance_ratio) + 1), explained_variance_ratio, label='寄与度', color='blue')
plt.plot(range(1, len(cumulative_explained_variance_ratio) + 1), cumulative_explained_variance_ratio, marker='o', color='red', label='累積寄与度')
plt.xlabel('主成分')
plt.ylabel('分散の割合')
plt.title('主成分分析の結果')
plt.legend()
plt.show()
return pcadf = pd.read_csv("o:/sample.tsv", delimiter="\t")
# 主成分分析を実施
apply_pca(df)主成分分析が簡単に行える便利な自作クラスを「【Python実践】データ分析の影の立役者!主成分分析(PCA)の使い方ガイド(コピペで使えるサンプルコード付き)」に掲載しています。併せてご覧ください。
まとめ
記事では、探索的データ解析(EDA)について詳しく解説しました。探索的データ解析(EDA)は、データの特徴、構造、異常値などを体系的に分析することで、仮説を導き出し、分析方針を選定するためのプロセスです。具体的には、以下の作業を行います。
- データの統計量を計算する
- データの分布を分析する
- 変数間の関係性を分析する
- データが待つパターンを分析する
また、Pythonのサンプルプログラムとして次のものを紹介しました。
- 総当たりによる散布図の描画
- 総当たりによる相関係数ヒートマップの描画
- 指定したラグの散布図の描画








コメント