本記事は「【成功の秘訣】現場で使えるデータ分析手順を体系的に解説」で紹介したモデルの選定に関する具体的な手順と、良く用いられるモデルのPythonサンプルコードを紹介しています
モデルの選定とは

これまでの過程において、最初の段階で分析方法を決定し、データ探索(事前分析)や探索的データ解析(EDA)を通じて仮説を立て、問題があれば分析方法の軌道修正を行いました。
モデルの選定とは、これまでの結果や知見に基づき、実際の分析で用いるモデルやアルゴリズムを選定する作業です。
例えば、センサーA、B、Cの値から容器の温度を予測するような場合、「ランダムフォレストを使った回帰モデルを作成する」がモデルの設定となります。
モデルの選定は、単に最も良い成績を示すモデルを選ぶだけではなく、モデルの解釈性や実行速度、リソースの消費なども考慮する必要があります。これにより、実際のビジネス環境や運用条件に適したモデルを導入することができます。
時間が限られている場合には、候補を1つに絞ることもありますが、通常はいくつかのアルゴリズムやモデルを試してみて、最も良い成績を示すものを選び、それに注力することもよくあります。
モデルの選定は次の手順で行います。
- 分析手法の選定
- モデルやアルゴリズムの選定
モデルの選定の重要性

モデルはデータからパターンや関係性を見つけ出し、未知のデータに対する予測を行うための枠組みです。従って、適切なモデルを選択できていないと、分析結果の妥当性や予測精度に大きな影響を与えます。
- 結果の信頼性: 適切なモデルを選択することで、分析結果の信頼性が向上します。選択したモデルがデータの特性や問題の性質に適合している場合、より正確な予測や洞察が得られるでしょう。
- 予測精度の向上: 適切なモデルは、未知のデータに対する予測精度を向上させることができます。良いモデルはデータの構造をうまく捉え、より正確な予測を提供します。
- 計算効率の向上: データ量が多い場合や計算リソースに制約がある場合、適切なモデルを選択することで計算効率が向上します。過度に複雑なモデルを選択すると計算時間が増加し、リソースの浪費につながります。
- 解釈性の向上: モデルの選定によって、そのモデルの結果や予測が解釈しやすくなる場合があります。特定のモデルは、どのような特徴が予測に影響を与えているかを明確に示すことができます。
モデルの選定手順

モデル/アルゴルズムは非常に多く存在するため全てを列挙することはできません。ここでは製造業でよく使われるメジャーなものを抜粋しています。
Pyhton で利用できるモデル/アルゴリズムのより詳しい情報は、 scikit learn公式サイト をご確認ください。
分析手法の選定
分析の目的とデータの特性に適した分析手法を選定します。
例えば、生産プロセスのデータを基に、類似する製品や生産ラインの特徴的なパターンを見つけたい場合は、「クラスタリング」分析手法を利用します。 逆に、製造設備の回転数と製造物の重量からベルトに掛かる圧力値を予測したい場合は、「回帰」分析を選びます。
分析目的と分析手法の選定ポイントは次の通りです。
| 分析目的 | 分析手法 | 選定ポイント | 教師データ |
|---|---|---|---|
| データをグループに分ける | クラスタリング | データをいくつかのグループに分けたい場合 | なし |
| カテゴリーを予測する | 分類 | 「良品」「不良品」や「犬」「猫」「鳥」など離散的なカテゴリに分類したい場合 | 必要 |
| 数値を予測する | 回帰 | 「気温」や「使用量」などの連続的な数値を予測したい場合 | 必要 |
| よく一緒に起こるパターンを見つける | アソシエーション分析 | 「定期点検では、よく部品Aと一緒にCが交換されている」など、発生頻度の高い組合せのパターンを把握したい場合 | なし |
| 重要な特徴を見つける | 特徴選択/抽出 | 「工場Aと工場Bにおいて、工場Aはエンジントラブルが多い」など、グループごとの特徴を把握したい場合 | なし |
| 異常なデータを見つける | 異常検知 | 閾値では検出できない複雑なパターンや条件において、いつもと違う状態を検知したい場合 | なし |
| データの次元を減らす | 次元削減 | 分析対象の項目が多すぎるため、項目数を減らしたい場合 クラスタリングの効率を上げたい場合。 | なし |
| 時系列データを分析する | 時系列分析 | 株価や気温変動のな時系列的に変化するデータにおいて、過去から未来を予測したい場合 | なし |
| テキストデータを分析する | テキストマイニング | テキストデータから「重要なキーワードの抽出」「名寄せ」「要約」などを行いたい場合 | なし |
| 画像データを分析する | 画像分析 | 画像分類や不良品検出など、画像を使って分析したい場合 | 必要 |
| データ間の関係や重要なノードやグループを見つける | ネットワーク分析 | 良く行われている画面遷移や操作手順などを可視化により把握したい場合 | なし |
モデルやアルゴリズムの選定
選定した分析手法に対応するモデルやアルゴリズムを選定します。
例えば、分析手法としてクラスタリングを選択した場合、単にグループ化したいだけならモデル/アルゴリズムに「K-means」を選択、階層的に可視化したい場合は「階層的クラスタリング」を選択します。
「回帰」を選択した場合、線形の予測で事足りる場合は「重回帰分析」、非線形で複雑な予測が必要な場合は勾配ブースティングを選択します。
分析手法とアルゴリズムの選定ポイントは次の通りです。
| 分析手法 | アルゴリズム | 選定ポイント |
|---|---|---|
| クラスタリング | K-means | - クラスタの数が事前に決まっている場合 - 簡単な実装と高速な計算が必要な場合 |
| 階層的クラスタリング | - 階層構造がデータに適している場合 - クラスタの数を明確に設定したくない場合 | |
| DBSCAN | - ノイズのあるデータや密度が異なるクラスタを検出したい場合 - クラスタの形が非球状である場合 | |
| 分類 | 決定木 | - 結果の解釈性が重要である場合 - データの前処理が少ない場合 |
| アンサンブル学習 | - 複数の弱学習器を組み合わせて性能を向上させたい場合 - モデルの分類性能が最重要視される場合 ランダムフォレスト、GBDT、LightGBM、XGBoost CatBoost、Adaboost | |
| サポートベクターマシン | - 非線形の分離が可能である場合 - 高次元のデータセットに適している場合 | |
| ニューラルネットワーク | - 複雑な非線形関係をモデル化したい場合 - 大規模なデータセットに対処する必要がある場合 | |
| 線形回帰 | 回帰分析 | - 線形関係があると仮定できる場合 - モデルの解釈性が重要である場合 |
| リッジ回帰 | - 多重共線性がある場合 - 過学習を抑制したい場合 | |
| LASSO | - 変数選択が重要である場合 - スパースな解が必要な場合 | |
| 非線形回帰 | アンサンブル学習 | - 複数の弱学習器を組み合わせて性能を向上させたい場合 - モデルの予測性能が最重要視される場合 ランダムフォレスト、GBDT、LightGBM、XGBoost CatBoost、Adaboost |
| サポートベクターマシン | - 高次元データや非線形な関係がある場合 - カーネル関数を使用して非線形な関係をモデル化できる | |
| カーネルリッジ回帰 | - リッジ回帰の拡張として、非線形な関係をモデル化したい場合 - カーネル関数を使用して非線形な関係を捉えることができる | |
| ニューラルネットワーク | -大量のデータがあり、複雑な非線形関係をモデル化したい場合 -多層のネットワークを構築することで、非常に複雑な関係を学習できる | |
| アソシエーション分析 | アプリオリ | - アイテム間の関連性を把握したい場合 - 頻出するアイテムセットを見つけたい場合 |
| FP-growth | - 大規模なデータセットに適用したい場合 - メモリ効率が重要な場合 | |
| 特徴選択/抽出 | TF-IDF | - テキストデータの重要な特徴を抽出したい場合 |
| 主成分分析 (PCA) 因子分析(FA) | - 多重共線性を解消したい場合 - データの次元削減が必要な場合 | |
| LDA | - クラス間の差異を最大化する特徴を抽出したい場合 | |
| 異常検知 | Isolation Forest | - 高次元のデータや大規模なデータに対しても有効な場合 - 外れ値が複数の特徴に影響される場合 |
| One Class SVM | - データの外れ値検出が目的である場合 - 線形と非線形のデータに対応する必要がある場合 | |
| LOF | - 局所的な外れ値を検出したい場合 - クラスタ内の密度が異なる場合 | |
| Auto Encoder | - 正常データからの再構成誤差を利用して異常を検出したい場合 - 非線形かつ複雑な特徴を持つデータに対応したい場合 | |
| 次元削減 | 主成分分析 (PCA) 因子分析(FA) | - 高次元データの可視化が必要な場合 - データの次元削減が必要な場合 |
| t-SNE | - 高次元データの構造を保持しつつ、低次元空間にマッピングしたい場合 | |
| LDA | - クラス間の差異を最大化してデータを次元削減したい場合 | |
| 時系列分析 | SARIMA | - 時系列データのトレンドや季節性をモデル化したい場合 |
| 指数平滑法 | - 短期的な予測が必要な場合 - 季節性やトレンドを考慮しない場合 | |
| LSTM | - 長期の依存関係を捉えたい場合 - 高度な時系列パターンの予測が必要な場合 | |
| テキストマイニング | BoW (Bag of Words) | - テキストデータの単語の出現頻度を考慮したい場合 |
| TF-IDF | - 単語の重要度を考慮したい場合 - テキストデータの特徴量を作成したい場合 | |
| Word2Vec | - 単語の意味的な関係性を捉えた | |
| 潜在変数モデリング | 主成分分析 (PCA) 因子分析(FA) | -観測できない潜在的な変数をモデル化 |
よく使われるモデルのプログラム例
決定木
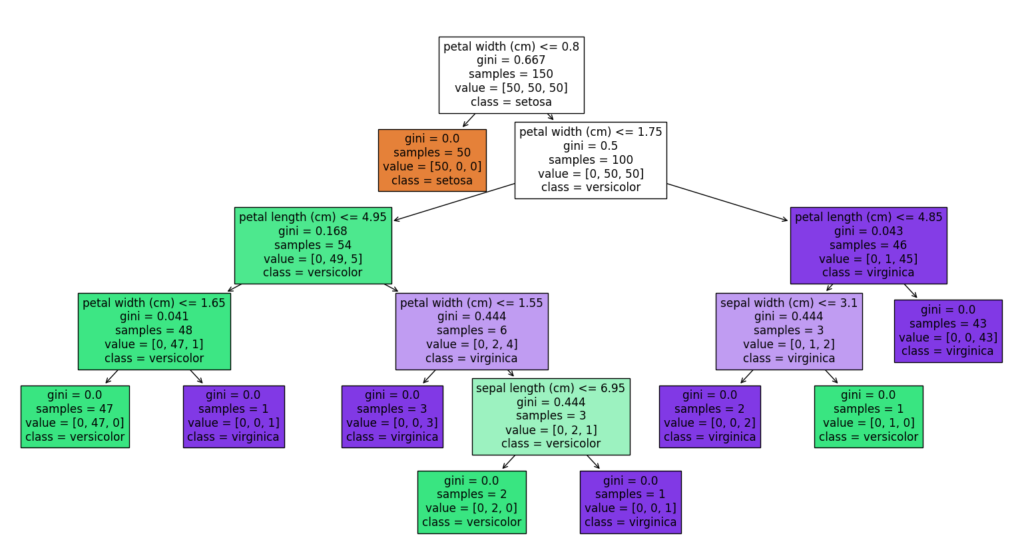
指定したDataFrameと目的変数のカラム、説明変数のカラムリスト、出力結果の保存ファイル名を指定することで、描画した決定木を png 形式の画像として出力するサンプルです。
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
import matplotlib.pyplot as plt
# データセットのロード
iris = load_iris()
X, y = iris.data, iris.target
# 決定木モデルの訓練
clf = DecisionTreeClassifier()
clf = clf.fit(X, y)
# 決定木のプロット
plt.figure(figsize=(20,10))
tree.plot_tree(clf, filled=True, feature_names=iris.feature_names, class_names=iris.target_names)
plt.show()重回帰分析
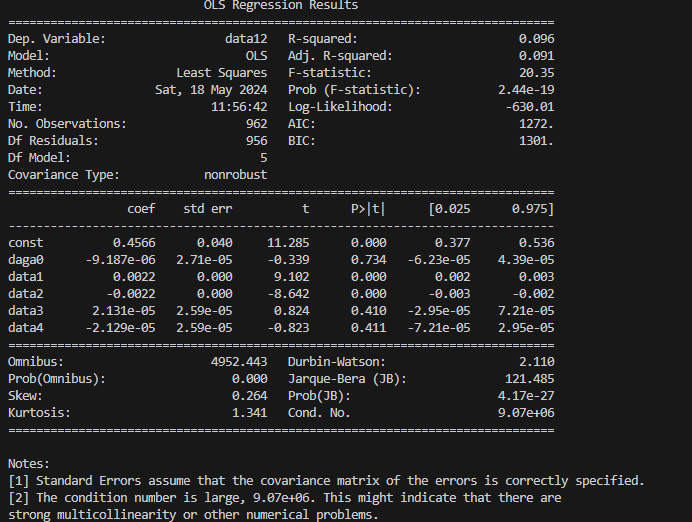
指定したDataFrameと目的変数のカラム、説明変数のカラムリストを渡すことで、重回帰分析を行うサンプルです。
import pandas as pd
import statsmodels.api as sm
def multiple_linear_regression(df, target_column, feature_columns):
"""
複数の特徴量を使用して重回帰分析を行う関数
Parameters:
df (pd.DataFrame): データフレーム
target_column (str): 目的変数のカラム名
feature_columns (list of str): 特徴量として使用するカラム名のリスト
Returns:
None: モデルのサマリーを表示
"""
# 特徴量と目的変数を分割
X = df[feature_columns]
y = df[target_column]
# 無限大と欠損値をチェックして取り除く
X = X.replace([float('inf'), float('-inf')], pd.NA).dropna()
y = y.loc[X.index] # Xの欠損値に対応するyの値も取り除く
# 定数項を追加
X = sm.add_constant(X)
# 最小二乗法でモデルを適合
model = sm.OLS(y, X).fit()
# モデルのサマリーを表示
# Print the summary of the regression model
print(model.summary())df = pd.read_csv("o:/sample.csv")
# 関数を呼び出して重回帰分析を実行
multiple_linear_regression(df, 'data12', df.columns[:5])ネットワーク図
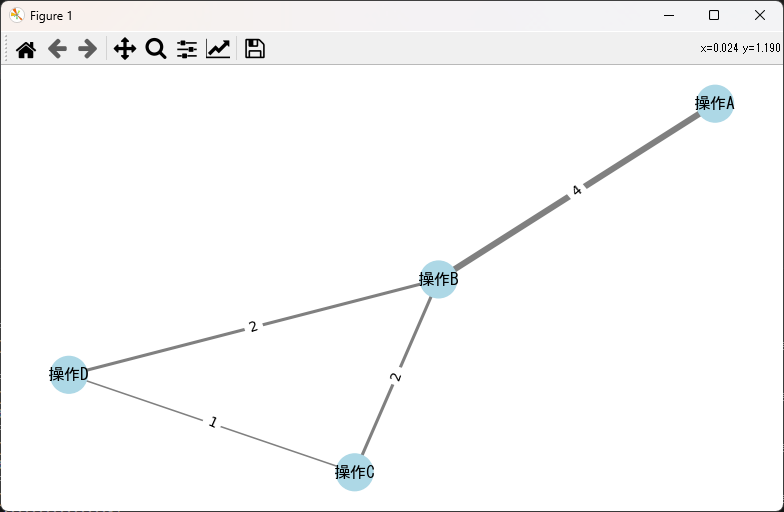
import networkx as nx
import matplotlib.pyplot as plt
def draw_weighted_graph_from_edges(edges, node_color="lightblue", edge_color="gray", seed=42):
"""
指定されたエッジのリストから重み付きのグラフを描画する関数。
引数:
edges (list of tuples): グラフのエッジを表すタプルのリスト。各タプルは2つのノードを持つ。
node_color (str): ノードの色。デフォルトは "lightblue"。
edge_color (str): エッジの色。デフォルトは "gray"。
seed (int): レイアウトのランダムシード。デフォルトは 42。
処理手順:
1. NetworkXグラフ `G` を初期化。
2. エッジのリストからエッジをグラフに追加。
3. 各エッジの出現回数をカウントし、エッジの重みを計算。
4. ノードの色とサイズを設定。
5. `spring_layout` に基づいてノードの位置を設定。
6. エッジの重みに基づいてエッジの太さを計算。
7. グラフを描画し、エッジの重みをラベルとして表示。
"""
# グラフの初期化
G = nx.Graph()
# エッジの追加
for edge in edges:
G.add_edge(*edge)
# エッジのカウント
edge_counts = {}
total = 0
for edge in edges:
total += 1
if edge in edge_counts:
edge_counts[edge] += 1
else:
edge_counts[edge] = 1
# エッジの重みの計算
edge_weights = {edge: round(count, 1) for edge, count in edge_counts.items()}
# ノードの色を設定
node_colors = [node_color] * len(G.nodes())
# ノードのサイズを設定
node_sizes = [700] * len(G.nodes())
# グラフの描画
pos = nx.spring_layout(G, seed=seed) # ノードの位置を設定
width = [10 * edge_weights[edge] / total for edge in G.edges()] # エッジの太さを計算
nx.draw(G, pos=pos, with_labels=True, font_family='MS Gothic',
node_size=node_sizes, width=width,
node_color=node_colors, edge_color=edge_color)
# エッジの重みを表示
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_weights)
# 描画の表示
plt.show()# エッジのリスト
edges = [('操作A', '操作B'), ('操作B', '操作C'), ('操作C', '操作D'), ('操作A', '操作B'), ('操作B', '操作C'), ('操作A', '操作B'), ('操作B', '操作D'),('操作A', '操作B'),('操作B', '操作D')]
# グラフの描画
draw_weighted_graph_from_edges(edges)まとめ
モデルの選定とは、これから行う分析に使用するモデルやアルゴリズムを決める作業を指します。
分析を開始する段階で、分析方針とともにモデルやアルゴリズムも選定しますが、事前分析やEDA(探索的データ分析)を通じて得られた結果から、当初の方針通りに進めるのか、それとも見直すのかを判断する作業も含まれます。
モデルの選定に際しては、まず「分析手法」を選び、その中から「モデル/アルゴリズム」を選択します。
分析手法やモデル/アルゴリズムには多くの種類があり、目的やデータの特性に応じて適切なものを選ぶことが重要です。選定時にはモデルの性能だけでなく、モデルの解釈性、実行速度、リソース消費なども考慮する必要があります。









コメント