製造業では、製品の品質向上、生産性の向上、コスト削減など、様々な課題が常に存在します。特に、製品不良の原因究明は、企業にとって喫緊の課題の一つです。
重回帰分析を使えば、製造工程における様々な要因が製品不良に与える影響を数値化し、根本的な原因を特定することができます。さらに、未来の製品不良数を予測することで、予防的な対策を立てることも可能です。
本記事では、Pythonを用いて、製造業における品質管理に重回帰分析を適用する方法を、具体的なコード例とともに解説します。
重回帰分析とは
重回帰分析は、ある事象(目的変数)に対して、複数の要因(説明変数)がどのように影響しているかを分析する統計学の手法です。
重回帰分析を行うことで、ある事象の発生にどのような要素が関わっているか(どのようなルールが存在するか)を把握することが可能であり、そのルールを使って将来どうなるかを予測することも可能になります。
より詳しい説明を知りたい方は、IM-Pressの「重回帰分析とは? ~目的から手順や注意点までわかりやすく解説~」が分かり易いです。
重回帰分析のメリット
- 複数の要因を同時に分析可能:
- 製造工程における不良率に影響を与える要因として、原材料の品質、機械の精度、作業者の経験など、複数の要因を同時に分析できます。
- これにより、単一の要因に注目するよりも、より包括的な分析が可能になり、問題解決の糸口を見つけやすくなります。
- 予測精度が高い:
- 過去のデータに基づいて、将来の製品不良率や生産量などを予測することができます。
- この予測値は、生産計画の立案や在庫管理などに活用できます。
- 因果関係の解明:
- どの要因が目的変数に最も大きな影響を与えているのかを特定することで、改善すべき点を明確にすることができます。
- 汎用性が高い:
- 製造業だけでなく、マーケティング、経済学など、様々な分野で活用できます。
重回帰分析のデメリット
- 線形関係を前提とする:
- 重回帰分析は、説明変数と目的変数の関係が線形であることを前提としています。非線形な関係がある場合は、他の分析手法を検討する必要があります。
- 多重共線性:
- 説明変数同士が強い相関関係にある場合、分析結果が不安定になることがあります。
- 例えば、原材料費と人件費が強い相関関係にある場合、どちらが目的変数に大きく影響しているのかを正確に判断できなくなることがあります。
- 外れ値の影響:
- データの中に外れ値が存在すると、分析結果に大きな影響を与えることがあります。
- 外れ値を適切に処理する必要があります。
- モデルの複雑化:
- 説明変数の数が多くなると、モデルが複雑になりすぎて、解釈が難しくなることがあります。
重回帰分析の落とし穴(見せかけの回帰)
重回帰分析は、複数の説明変数を用いて一つの目的変数を予測する強力な統計的手法です。しかし、その利用には注意すべき落とし穴が存在します。その中でも特に重要なのが、見せかけの回帰(Spurious Regression)です。
見せかけの回帰とは?
見せかけの回帰とは、本来は因果関係がないにもかかわらず、統計的な分析の結果、あたかも強い関連性があるように見えてしまう現象のことです。これは特に、非定常な時系列データを重回帰分析に用いた場合に起こりやすくなります。
非定常な時系列データとは、その統計的な性質(平均、分散、自己相関など)が時間とともに変化する時系列データのことです。言い換えると「時間によってデータの振る舞いが安定していない」データであり、ランダムウォークもその1つです。
見せかけの回帰が起こる理由
見せかけの回帰が起こる理由は、次の通りです。
- 共通の非定常性:
的変数と一つ以上の説明変数が、それぞれ独立にランダムウォークのような非定常な動きをしている場合、時間とともに偶然同じような傾向を示すことがあります。これにより、統計的な分析では有意な関係があるように見えてしまいます。 - 見えない共通要因
分析に含めていない共通の要因が、目的変数と複数の説明変数に影響を与えている場合、直接的な因果関係がないにもかかわらず、相関が高くなることがあります。
見せかけの回帰によって得られた回帰モデルは、現実とは異なる解釈を生み出し、誤った意思決定につながる可能性があります。例えば、実際には無関係な変数の間に強い影響関係があると誤認し、効果のない対策を講じてしまうなどが考えられます。
見せかけの回帰への対処法
回帰分析の結果が正しいか否か(見せかけの回帰によるものでないこと)を検証するために、以下の手段を講じます。
- データの定常性の確認
分析に用いるすべての時系列データに対して、単位根検定(ADF検定、KPSS検定など)を実施し、定常性を確認します。 - 差分系列の利用
データが非定常である場合は、単純に元の系列を用いるのではなく、差分系列(時点間の変化量)を用いた分析を検討します。 - 共和分分析の検討
目的変数と複数の説明変数の間に長期的な均衡関係(共和分関係)が存在するかどうかを分析します。共和分関係がある場合は、誤差修正モデル(ECM)などの適切なモデルを用いることが考えられます。 - 理論的考察の重視
統計的な結果だけでなく、分析対象の分野に関する理論的な考察を行い、得られた関係性が理にかなっているかを検討します。 - モデル診断の徹底
回帰分析後には、残差の自己相関などをチェックし、モデルの妥当性を評価します。 - 安易な因果関係の結論を避ける
高い相関関係や統計的に有意な回帰係数が得られたとしても、それだけで安易に因果関係があると結論付けるのではなく、慎重な解釈を心がけることが重要です。
重回帰分析は強力なツールですが、特に時系列データを扱う際には、見せかけの回帰という落とし穴を理解し、適切な対策を講じることが不可欠です。データの本質的な関係性を捉え、誤った結論を避けるために、常に注意深い分析を心がけましょう。
製造業での用途
重回帰分析は、製造業において様々な場面で活用され、生産性の向上や品質の安定化に貢献しています。以下に、具体的な活用例をいくつか挙げます。
- 不良品発生原因の特定
製品の不良率に影響を与える複数の要因(原材料の品質、製造温度、機械の振動など)を分析し、最も影響の大きい要因を特定します。これにより、不良品発生の原因を特定し、対策を講じることができます。 - 製品特性との相関分析
製品の特性(強度、耐久性など)と製造工程における様々なパラメータとの関係性を分析し、製品品質の向上に繋げることが可能です。 - 生産量の予測: 過去の生産データや市場動向を基に、将来の製品需要を予測し、最適な生産計画を立案できます。
- 生産リードタイムの予測: 製造工程における各工程の所要時間を予測し、納期管理の精度向上に役立ちます。
- 原価計算の最適化: 製品原価に影響を与える様々な要因を分析し、コスト削減のための施策を立案できます。
重回帰分析で用いる2種類のライブラリ
python で重回帰分析を行う場合、statsmodels と sklearn の2通りのライブラリがあり、それぞれ以下の特徴を持っています。
| 項目 | statsmodelsによる重回帰分析 | sklearnによる重回帰分析 |
|---|---|---|
| 特徴 | 【統計学的な推論】 モデルの係数、p値、信頼区間など、統計学的な指標を詳細に提供し、変数間の関係性を深く理解したい場合に適しています。 【回帰診断】 残差プロット、影響力のある観測値の検出など、モデルの診断ツールが充実しており、モデルの妥当性を確認したい場合に有効です。 【時系列分析、パネルデータ分析など】 重回帰分析だけでなく、様々な統計モデルをサポートしています。 | 【機械学習】 様々な機械学習アルゴリズムを実装しており、予測精度を向上させることに重点を置いています。 【パイプライン】 前処理から評価まで、一連の処理をパイプラインで繋げることができ、効率的なデータ分析が可能です。 【大規模データ】 大規模なデータセットに対しても高速に処理できます。 |
| 目的 | 変数間の関係性を深く理解したい場合 モデルの係数の意味を詳しく理解したい場合 | 様々なアルゴリズムを試して、 最適な予測モデルを作りたい場合 パイプライン機能を使って、大規模な データセットを効率的に処理したい場合 |
statsmodels は統計的な指標が多く用意されており、分析結果から原因や要因を深く理解したい用途に向いています。一方 sklearn は、Lasso、Ridge、ElasticNetなど様々なアルゴリズムが用意されており、予測精度を追求したい用途に向いています。
インストール方法
pip コマンドで、次の2つのライブラリをインストールしてください。
pip install scikit-learn
pip install statsmodels
statsmodelsによる重回帰分析の実行方法
statsmodelsで重回帰分析を行う場合、データ数が20以上ないと警告が表示されます。今回はリストの中に for文を記述して、30個のデータを生成しています。
モデルの作成(statsmodels)
import pandas as pd
import numpy as np
import statsmodels.api as sm
import pickle
# データをDataFrameに格納
data = {'特徴量1': [x+5 for x in range(30)],
'特徴量2': [x-5 for x in range(30)],
'特徴量3': [x+3 for x in range(30)],
'目的変数': [x for x in range(30)]
}
df = pd.DataFrame(data)
# 説明変数と目的変数の分割
X = df[['特徴量1', '特徴量2', '特徴量3']]
y = df['目的変数']
# 定数項を追加
X = sm.add_constant(X)
# OLS (Ordinary Least Squares) モデルの構築と適合
model = sm.OLS(y, X).fit()
# モデルをファイルに保存
with open('./mlr_model.pkl', 'wb') as f:
pickle.dump(model, f)
# モデルのサマリーを表示
print(model.summary())プログラムを実行すると、下記の内容が表示されます。
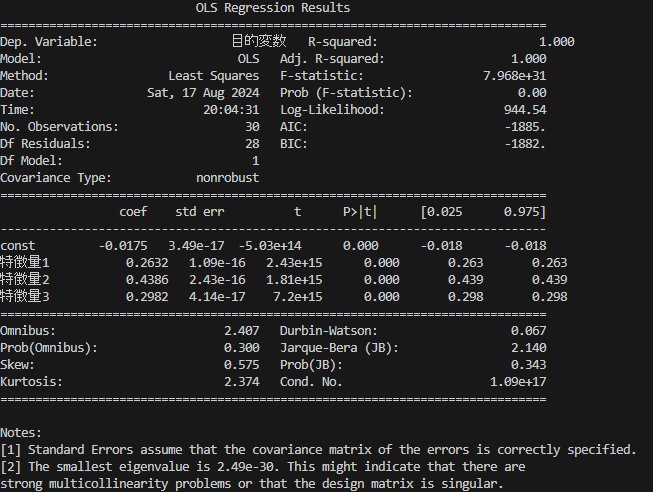
| 項目名 | 日本語名 | 意味 |
|---|---|---|
| Dep. Variable | 目的変数 | 予測または説明しようとしている変数 |
| R-squared | 決定係数 | モデルの適合度を示す指標 |
| Model | モデル | 使用した回帰モデル |
| Method | 方法 | 使用した統計手法 |
| Least Squares | 最小二乗法 | 回帰分析の方法の一つ |
| F-statistic | F統計量 | モデル全体の有意性を検定する統計量 |
| Prob (F-statistic) | F統計量の確率 | F統計量の有意確率 |
| Log-Likelihood | 対数尤度 | モデルの尤度の対数 |
| No. Observations | 観測数 | データの観測数 |
| AIC | AIC | 赤池情報量基準 |
| Df Residuals | 残差自由度 | 残差の自由度 |
| BIC | BIC | ベイズ情報量基準 |
| Df Model | モデル自由度 | モデルの自由度 |
| Covariance Type | 共分散タイプ | 共分散のタイプ |
| coef | 回帰係数 | 回帰係数 |
| std err | 標準誤差 | 標準誤差 |
| P>|t| | t値 | t検定の統計量 |
| [0.025 0.975] | 信頼区間 | 95%信頼区間 |
| const | 定数 | 定数項 |
| Omnibus | オムニバス | 残差の正規性を検定する統計量 |
| Durbin-Watson | ダービン・ワトソン | 残差の自己相関を検定する統計量 |
| Prob(Omnibus) | オムニバスの確率 | オムニバス検定の有意確率 |
| Jarque-Bera (JB) | ジャック・ベラ | 残差の正規性を検定する統計量 |
| Skew | 歪度 | 残差の歪度 |
| Prob(JB) | JBの確率 | ジャック・ベラ検定の有意確率 |
| Kurtosis | 尖度 | 残差の尖度 |
| Cond. No. | 条件数 | 行列の条件数 |
予測(statsmodels)
作成したモデルを使って予測するサンプルです。前述のサンプルで保存したモデルファイルを読み込み、予測を行っています。
モデルファイルに含まれる定数項を、予測対象のデータに追加しているところがポイントです。
import pandas as pd
import statsmodels.api as sm
import pickle
with open('./mlr_model.pkl', 'rb') as f:
model = pickle.load(f)
# 新しいデータ点
new_data = pd.DataFrame({'特徴量1': [2.8], '特徴量2': [1.8], '特徴量3': [3.2]})
# モデルに含まれる定数項を、予測対象のデータ点に追加
new_data = sm.add_constant(new_data, has_constant='add')
# 予測
predicted = model.predict(new_data)
# 予測結果の表示
print(predicted)実行すると次の結果が表示されます。
0 2.463158
dtype: float64
scikit-learnによる重回帰分析の実行方法
モデルの作成(scikit-learn)
下記は、statsmodelsの重回帰分析プログラムを scikit-learn 向けに書き換えたものです。
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Lasso, Ridge, ElasticNet
# データをDataFrameに格納
data = {'特徴量1': [x+5 for x in range(30)],
'特徴量2': [x-5 for x in range(30)],
'特徴量3': [x+3 for x in range(30)],
'目的変数': [x for x in range(30)]
}
df = pd.DataFrame(data)
# 説明変数と目的変数の分割
X = df[['特徴量1', '特徴量2', '特徴量3']]
y = df['目的変数']
# 線形回帰モデルの構築と適合
# 他のモデルを使う場合は、下記の1行を書き換えて下さい。
model = LinearRegression()
# モデルの作成
model.fit(X, y)
# モデルをファイルに保存
import pickle
with open('./slr_model.pkl', 'wb') as f:
pickle.dump(model, f)
# モデルの係数と切片を表示
print('係数:', model.coef_)
print('切片:', model.intercept_)実行した結果は次の通りです。statsmodels と比べて、得られる統計情報が極端に少ないことが分かります。
係数: [0.33333333 0.33333333 0.33333333]
切片: -0.9999999999999982
重回帰分析で使えるモデルには次のものがあります。データに合わせて最適なアルゴリズムを選ぶことで、より精度の高い予測が可能になります。
| 選択可能なアルゴリズム | 名前 | 特徴 | 代表的な引数 |
|---|---|---|---|
| LinearRegression() | 線形回帰 | 最も基本的な線形回帰モデル。正則化なし。 | fit_intercept=True (切片を計算するかどうか) |
| Lasso() | Lasso | L1正則化による特徴量選択と係数の縮小。 | alpha=0.1 (正則化の強さ) |
| Ridge() | Ridge | L2正則化による係数の縮小。 | alpha=0.1 (正則化の強さ) |
| ElasticNet() | ElasticNet | L1とL2正則化の組み合わせ。 | alpha=0.1, l1_ratio=0.5 (L1正則化の割合) |
| BayesianRidge() | ベイズリッジ回帰 | ベイズ的なアプローチに基づき、係数の事後分布を推定。 | n_iter=3000 (反復回数) |
| ARDRegression() | ARD回帰 | 各特徴量の重要度を自動的に学習。 | alpha_1=1e-06, alpha_2=1e-06 (事前分布の精度) |
| LassoLars() | LassoLars | LassoとLeast Angle Regressionを組み合わせたアルゴリズム。 | alpha=0.1 (正則化の強さ) |
| OrthogonalMatchingPursuit() | Orthogonal Matching Pursuit | 貪欲なアルゴリズムで特徴量を選択。 | n_nonzero_coefs=5 (非ゼロ係数の最大数) |
| Perceptron() | パーセプトロン | 単純なニューラルネットワーク。 | eta0=0.1 (学習率), tol=1e-3 (収束判定の閾値) |
| PassiveAggressiveRegressor() | パッシブアグレッシブ回帰 | オンライン学習に適している。 | C=1.0 (ペナルティパラメータ) |
| SGDRegressor() | 確率的勾配降下法回帰 | 大規模データセットに適している。 | eta0=0.01 (初期学習率), penalty='l2' (正則化の種類) |
| TheilSenRegressor | Theil-Sen回帰 | 外れ値に強いロバストな回帰。 | random_state=None (乱数シード) |
別のモデルを選択する場合は、下記の XXXXX をモデルに合わせて書き換えてください。
# モデルをインポート
from sklearn.linear_model import XXXXX
~~~~省略~~~~
# 線形回帰モデルの構築と適合
model = XXXXX
# モデルの作成
model.fit(X, y)
予測(scikit-learn)
import pandas as pd
from sklearn.linear_model import LinearRegression
import pickle
# モデルを読み込み
with open('./slr_model.pkl', 'rb') as f:
model = pickle.load(f)
# 新しいデータ点
new_data = pd.DataFrame({'特徴量1': [2.8], '特徴量2': [1.8], '特徴量3': [3.2]})
# 予測
predicted = model.predict(new_data)
# 予測結果の表示
print(predicted)実行すると、下記の通り予測結果が表示されます。
[1.6]
重回帰分析を手軽に実行できるMultipleLinearRegression自作クラス
指定したDataFrameと目的変数のカラム、説明変数のカラムリストを渡すことで、重回帰分析を行うMultipleLinearRegression クラスを作りました。重回帰分析のライブラリは statsmodels を使っています。
下記は使い方のサンプルです。
import pandas as pd
from multiple_linear_regression import MultipleLinearRegression
# データをDataFrameに格納
data = {'特徴量1': [x+5 for x in range(30)], # 特徴量1のデータ
'特徴量2': [x-5 for x in range(30)], # 特徴量2のデータ
'特徴量3': [x+3 for x in range(30)], # 特徴量3のデータ
'目的変数': [x for x in range(30)] # 目的変数のデータ
}
df = pd.DataFrame(data) # データをDataFrameに変換
# MultipleLinearRegressionクラスのインスタンスを作成
ml = MultipleLinearRegression()
# 線形回帰モデルの構築と適合
model = ml.analyze('目的変数', ['特徴量1', '特徴量2', '特徴量3'], df=df)
# モデルの概要を表示
summary = ml.summary
print(summary)
# モデルの精度を表示(モデル作成時のデータを使って精度を評価)
eval = ml.evaluate(df)
print(eval)
# 予測したいデータを作成
new_data = {'特徴量1': [5,4,3], # 特徴量1のデータ
'特徴量2': [5,3,2], # 特徴量2のデータ
'特徴量3': [3,3,5], # 特徴量3のデータ
'目的変数': [2,4,1] # 目的変数のデータ
}
new_df = pd.DataFrame(new_data) # データをDataFrameに変換
# 引数で与えられたデータフレームに基づいて予測を行う
ml.predict(new_df,['特徴量1', '特徴量2', '特徴量3'])
# 予測結果を表示
print(ml.predict_result)プログラムを実行すると、下記が表示されます。
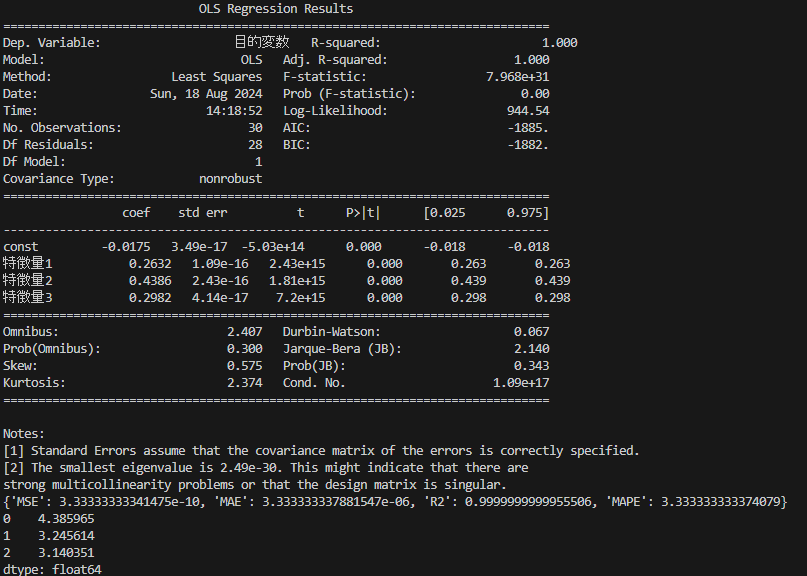
MultipleLinearRegression クラスに実装されているメソッドは次の通りです。
| メソッド名 | 説明 | 引数 | 戻り値 |
|---|---|---|---|
| __init__ | クラスのインスタンスを初期化するメソッド。 | なし | インスタンス |
| read_csv | ファイルからデータを読み込むメソッド。 | file_name (str): 読み込むファイルのパス encoding (str): ファイルのエンコーディング (省略時=“shift-jis”) | なし |
| analyze | 複数の特徴量を使用して重回帰分析を行うメソッド。 | target_column (str): 目的変数のカラム名 feature_columns (list of str): 特徴量のカラム名のリスト df (DataFrame): データフレーム (省略時はself.df) | モデル |
| save_model | モデルをファイルに保存するメソッド。 | model_path (str): 保存するファイルのパス | なし |
| load_model | モデルをファイルから読み込むメソッド。 | model_path (str): 読み込むファイルのパス (省略時はself.model_path) | モデル |
| predict | 予測を行うメソッド。 | df (DataFrame): 予測に使用するデータフレーム feature_columns (list of str): 特徴量のカラム名のリスト (省略時はself.feature_columns) | 予測結果 |
| evaluate | モデルの精度を評価するメソッド。 | df (DataFrame): 評価に使用するデータフレーム (省略時はself.df) | 精度評価の結果 (dict) MSE:平均二乗誤差 MAE:平均絶対誤差 R2:決定係数 MAPE:平均絶対パーセント誤差 |
ソースコード
import pandas as pd
import numpy as np
import statsmodels.api as sm
import pickle
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
class MultipleLinearRegression:
def __init__(self):
# 初期化メソッド
self.df = None # モデル作成時に用いるDataFrame(analyze or read_csvでセット)
self.model = None # モデル(analyzでセット)
self.summary = None # モデル作成時の統計情報
self.predict_result = None # 予測結果(predictでセット)
self.target_column = None # 目的変数のカラム名(analyzeでセット)
self.feature_columns = None # 説明変数のカラム名リスト(analyzeでセット)
self.model_path = None # モデルパス(save_modelでセット)
self.evaluation_results = {} # 予測精度(evaluateでセット)
self.residue = [] # 残差()
def read_csv(self, file_name, encoding="shift-jis"):
"""
ファイルからデータを読み込むメソッド
:param file_name: 読み込むファイルのパス (str)
:param encoding: ファイルのエンコーディング (str)
"""
self.df = pd.read_csv(file_name, encoding=encoding)
def analyze(self, target_column, feature_columns, df=None):
"""
複数の特徴量を使用して重回帰分析を行うメソッド
Parameters:
target_column (str): 目的変数のカラム名
feature_columns (list of str): 特徴量として使用するカラム名のリスト
df (DataFrame): データフレーム
Returns:
None: モデルのサマリーを表示
"""
# 引数のdfがNoneでないならself.dfにセット
if df is not None:
self.df = df
self.target_column = target_column
self.feature_columns = feature_columns
# 特徴量と目的変数を分割
X = self.df[feature_columns]
y = self.df[target_column]
# 定数項を追加
X = sm.add_constant(X)
# 最小二乗法でモデルを適合
self.model = sm.OLS(y, X).fit()
# 統計情報をプロパティに保存
self.summary = self.model.summary()
return self.model
def save_model(self, model_path):
"""
モデルをファイルに保存するメソッド
:param model_path: 保存するファイルのパス (str)
"""
self.model_path = model_path
with open(model_path, 'wb') as f:
pickle.dump(self.model, f)
def load_model(self, model_path=None):
"""
モデルをファイルから読み込むメソッド
:param model_path: 読み込むファイルのパス (str)
"""
if model_path is None:
model_path = self.model_path
with open(model_path, 'rb') as f:
self.model = pickle.load(f)
return self.model
def predict(self, df, feature_columns=None):
"""
予測を行うメソッド
:param df: 予測に使用するデータフレーム (DataFrame)
:param feature_columns: 特徴量として使用するカラム名のリスト (list of str)
"""
# 引数のfeature_columnsがNoneならself.feature_columnsを使う
if feature_columns is None:
feature_columns = self.feature_columns
# feature_columnsがNoneでなければ、feature_columnsのカラムのみ抽出
if feature_columns is not None:
df = df[feature_columns]
# モデルに含まれる定数項を、予測対象のデータ点に追加
new_data = sm.add_constant(df, has_constant='add')
# 予測
self.predict_result = self.model.predict(new_data)
return self.predict_result
def evaluate(self,df = None):
"""
モデルの精度を評価するメソッド
:param df: 予測に使用するデータフレーム (DataFrame)
:return: 精度評価の結果 (dict)
"""
# df が None から self.df を使う
if df is None:
df = self.df
# 予測を行う
predictions = self.predict(df, self.feature_columns)
# 実際の値(引数のdfがNoneなら、self.df を使う)
actual = df[self.target_column]
# 残差
self.residue = actual - predictions
# 値が0だと精度計算でエラーになるため、ゼロを小さな値に置き換える。
actual = actual.replace(0, 0.0001)
# 評価指標を計算
mse = mean_squared_error(actual, predictions) # 平均二乗誤差 (Mean Squared Error)
mae = mean_absolute_error(actual, predictions) # 平均絶対誤差 (Mean Absolute Error)
r2 = r2_score(actual, predictions) # 決定係数 (R-squared)
mape = np.mean(np.abs((actual - predictions) / actual)) * 100 # 平均絶対パーセント誤差 (Mean Absolute Percentage Error)
# 結果を辞書で返す
self.evaluation_results = {
'MSE': mse,
'MAE': mae,
'R2': r2,
'MAPE': mape
}
return self.evaluation_resultsまとめ
本記事では、重回帰分析の特徴と製造業における用途、そしてPythonを使った重回帰分析の方法について、具体的なサンプルコードを使って詳しく解説しました。
Pythonで重回帰分析を行う場合、 statsmodels と scikit-learn の選択肢がありますが、statsmodels は詳細な統計情報が得られ、scikit-learn は試せるアルゴリズムが豊富という特徴があるので、目的に応じて使い分けが必要です。
重回帰分析は、製造業における様々な課題解決に役立つ強力なツールであり、Pythonを用いることで、誰でも簡単に重回帰分析を実践することができます。
本記事を参考に、ぜひご自身のデータ分析に活かしてみてください。








コメント