K-meansクラスタリングは、大量のデータを自動的にグループ分けするアルゴリズムで、製造現場における異常検知や、部品の品質分類、設備の稼働状態の監視など、さまざまな場面で利用できます。
この記事では、製造業における具体的な活用例を交えながら、K-meansクラスタリングの基本的な使い方と実装方法を解説します。
コピペで簡単にクラスタリングが行える自作クラスも公開していますので、すぐに実践したい方は、ぜひご一読ください。
K-meansとは
K-meansは、データをグループ化(クラスタリング)するための代表的なアルゴリズムの一つです。特にシンプルで実装しやすく、小規模から大規模なデータセットまで幅広い用途で利用されています。その名前の通り、データをK個のクラスタ(グループ)に分けるのが目的です。
アルゴリズムの概要
K-meansの基本的な手順は以下の通りです。
- 初期クラスタ中心(セントロイド)の設定
最初にデータ内の任意の位置にK個のクラスタ中心をランダムに配置します。 - データポイントの割り当て
各データポイントを、最も近いクラスタ中心に割り当てます。距離の計算には、主にユークリッド距離が使用されます。 - クラスタ中心の再計算
割り当てられたデータポイントの平均を計算し、その値を新しいクラスタ中心とします。 - 収束条件の確認
データポイントの割り当てが変化しなくなるか、クラスタ中心の移動が微小になるまで、手順2と3を繰り返します。
K-meansのメリット
- 計算が高速
K-meansはシンプルな計算で済むため、大規模データでも効率的に動作します。 - 直感的に理解しやすい
データを「距離」と「平均」に基づいて分けるというシンプルなルールで動くため、初心者にも扱いやすいアルゴリズムです。 - 多用途に利用可能
マーケティングのセグメンテーション、異常検知、画像圧縮など、さまざまな分野で利用されています。
K-meansの課題
- 初期値依存
ランダムに設定する初期クラスタ中心により、最終的な結果が異なることがあります。この問題を改善するために、「K-means++」といった初期値設定手法が提案されています。 - クラスタ数の指定が必要
Kの値(クラスタ数)をあらかじめ設定する必要があるため、適切な値を選ぶには試行錯誤やエルボー法などの評価手法が必要です。 - 非球形データへの弱さ
K-meansは球形(円形や球体状)のクラスタを想定しているため、非球形のデータ分布や異なる密度を持つクラスタには不向きです。
クラスタリングに必要なモジュールのインストール
クラスタリングを実装するには、Pythonとscikit-learnライブラリが必要です。以下のコマンドで必要なライブラリをインストールできます。
pip install scikit-learn
pip install numpy
pip install pandas
pip install matplotlib
K-meansを使ったクラスタリングの実装例
K-meansクラスタリングは、最も一般的なクラスタリング手法の一つです。データをユーザーが指定した数のクラスタに分類するために使用されます。K-meansはクラスタの数(n_clusters)を事前に指定する必要があります。例えば、n_clusters=3と指定すると、データを3つのクラスタに分けます。
from sklearn.cluster import KMeans
# 5個の説明変数を持つ6組分のテストデータを生成
data = [
[5.1,3.5,1.4,0.2,0.3],
[4.9,3.0,1.4,0.2,0.4],
[4.7,3.2,1.3,0.2,0.3],
[4.5,3.1,1.5,0.2,0.3],
[5.0,3.6,1.4,0.2,0.4],
[4.6,3.1,1.3,0.2,0.3]
]
# K-meansクラスタリングの実行
kmeans = KMeans(n_clusters=3)
kmeans.fit(data)
# クラスタリング結果
labels = kmeans.labels_
centroids = kmeans.cluster_centers_
print("====分類結果====");
print(labels)
print("====クラスタの中心座標====")
print(centroids)kmeans.labels_に分類結果が、kmeans.cluster_centers_にクラスタ分類した際のセントロイド(中心座標)が格納されます。
====分類結果====
[0 2 1 1 0 1]
====クラスタの中心座標====
[[5.05 3.55 1.4 0.2 0.35 ]
[4.6 3.13333333 1.36666667 0.2 0.3 ]
[4.9 3. 1.4 0.2 0.4 ]]
3次元以下(説明変数が3以下)なら、matplotlib 等でグラフ化が可能ですが、それ以上(今回は5次元)になるとグラフ化できないため、主成分分析(PCA)などで次元削減を行う必要があります。
パラメータについて
| パラメータ | 説明 |
|---|---|
| n_clusters | 分類するクラスタの数を指定します。例えば、n_clusters=3は、データを3つのクラスタに分類することを意味します。適切なクラスタ数を選ぶことが重要であり、エルボー法やシルエットスコアを用いて、最適なクラスタ数を見つける方法があります。 |
| init | セントロイドの初期値の設定方法を指定します。一般的にはk-means++が使用され、これはクラスタ間の初期値の距離を最大化します。 |
| max_iter | セントロイドの再計算を繰り返す最大回数を指定します。デフォルトは300回です。 |
| random_state | 再現性のための乱数シードを設定します。これにより、同じデータセットで実行するたびに同じ結果を得ることができます。 |
最適なクラスタ数を見つける
データをいくつのクラスタ n_clustersに分割すれば良いかは悩みの種ですが、エルボー法やシルエットスコアと呼ばれる手法を用いることで、機械的に最適なクラスタ数を導き出すことができます。
エルボー法(Elbow Method)
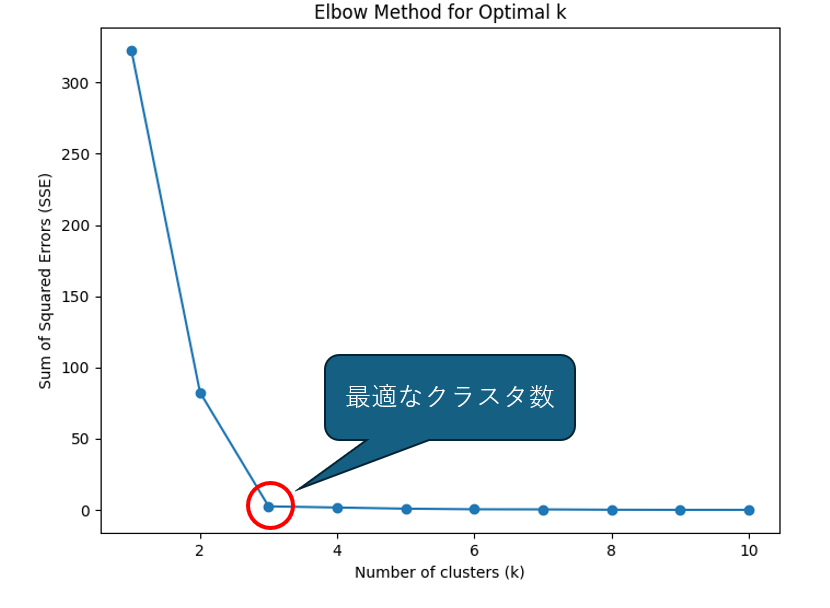
エルボー法は、適切なクラスター数を決定するための方法です。クラスター数を変えながらクラスタリングを行い、各クラスター数に対する全てのデータポイントの距離の総和(またはセントロイドの距離)を計算します。その結果をグラフにプロットし、クラスター数の増加に伴う総和の変化を観察します。
理想的なクラスター数は、グラフの「エルボー」のような曲線の曲がり角で、この点で総和の増加が鈍化することが多いです。この「エルボー」の位置が、適切なクラスター数として選ばれます。
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
# データの生成
data = [
[1.0, 2.0], [1.2, 2.2], [0.8, 1.8], [1.3, 2.3], [0.7, 1.7],
[5.0, 6.0], [5.3, 6.3], [4.7, 5.7], [5.4, 6.4], [4.6, 5.6],
[9.0, 10.0], [9.3, 10.3], [8.7, 9.7], [9.4, 10.4], [8.6, 9.6]
]
# エルボー法のためのSSE(Sum of Squared Errors)を計算
sse = []
k_range = range(1, 11)
for k in k_range:
kmeans = KMeans(n_clusters=k, random_state=0).fit(data)
sse.append(kmeans.inertia_)
# エルボー法の結果をプロット
plt.figure(figsize=(8, 6))
plt.plot(k_range, sse, marker='o')
plt.title('Elbow Method for Optimal k')
plt.xlabel('Number of clusters (k)')
plt.ylabel('Sum of Squared Errors (SSE)')
plt.show()シルエットスコア(Silhouette Score)
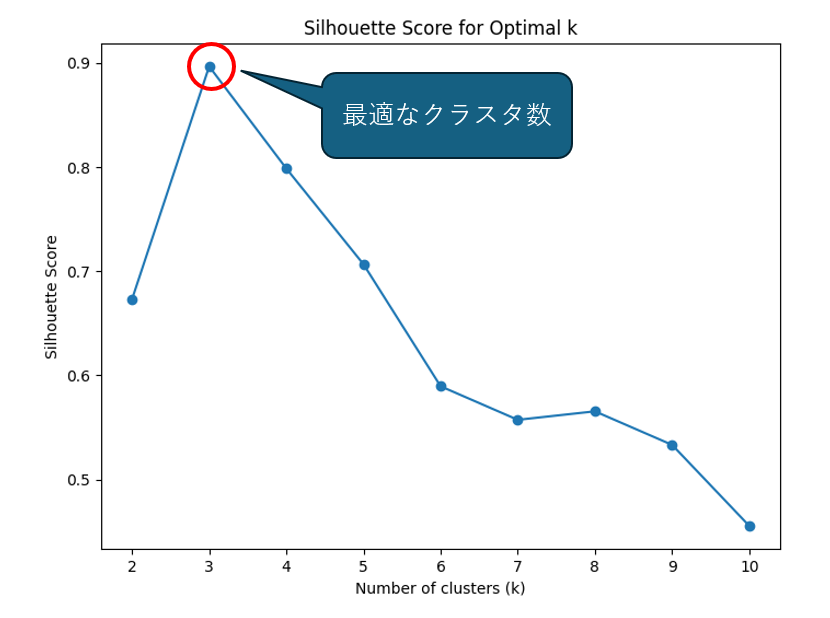
シルエットスコア(Silhouette Score)は、クラスタリングの品質を評価するための指標です。各データポイントに対して、そのデータポイントが自分のクラスターに属する程度(内部クロスバリエーション)と、他のクラスターに属する程度(外部クロスバリエーション)を計算し、その差をシルエットスコアとして表します。
シルエットスコアは、-1から1までの値を取り、1に近いほどクラスタリングの品質が高いことを示します。0に近い場合は、データポイントが自分のクラスターと他のクラスターの間で境界線上にあることを示し、負の値はクラスター間の重複を示します。
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
# データの生成
data = [
[1.0, 2.0], [1.2, 2.2], [0.8, 1.8], [1.3, 2.3], [0.7, 1.7],
[5.0, 6.0], [5.3, 6.3], [4.7, 5.7], [5.4, 6.4], [4.6, 5.6],
[9.0, 10.0], [9.3, 10.3], [8.7, 9.7], [9.4, 10.4], [8.6, 9.6]
]
# シルエットスコアの計算
silhouette_scores = []
k_range = range(2, 11) # シルエットスコアはk=2以上で計算
for k in k_range:
kmeans = KMeans(n_clusters=k, random_state=0).fit(data)
score = silhouette_score(data, kmeans.labels_)
silhouette_scores.append(score)
# シルエットスコアの結果をプロット
plt.figure(figsize=(8, 6))
plt.plot(k_range, silhouette_scores, marker='o')
plt.title('Silhouette Score for Optimal k')
plt.xlabel('Number of clusters (k)')
plt.ylabel('Silhouette Score')
plt.show()
可視化
可視化は、クラスタリング対象のデータを単純に散布図でプロットすることになりますが、その際にクラスタリング結果(番号)に応じて色分けすると当時に、中心座標も描画します。
また、ここでは2次元、3次元データの可視化方法と合わせて、多次元データを次元削減して可視化する具体的な方法も紹介します。
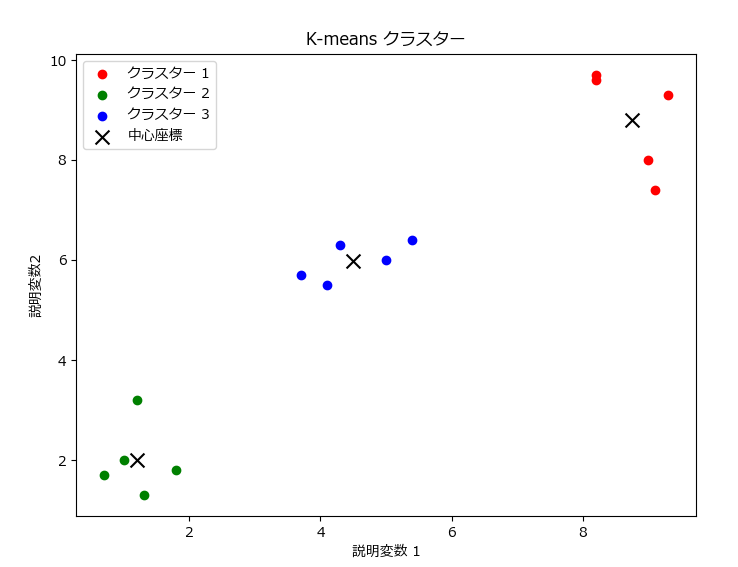
2次元データのクラスタリング結果を可視化
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
# 2次元のデータ15個を生成
data = [
[1.0, 2.0], [1.2, 3.2], [1.8, 1.8], [1.3, 1.3], [0.7, 1.7],
[5.0, 6.0], [4.3, 6.3], [3.7, 5.7], [5.4, 6.4], [4.1, 5.5],
[9.0, 8.0], [9.3, 9.3], [8.2, 9.7], [9.1, 7.4], [8.2, 9.6]
]
# K-meansクラスタリングの実行
kmeans = KMeans(n_clusters=3)
kmeans.fit(data)
# クラスタリング結果の取得
labels = kmeans.labels_
centroids = kmeans.cluster_centers_
# クラスタリング結果の可視化
plt.figure(figsize=(8, 6))
colors = ['r', 'g', 'b']
for i in range(3):
plt.scatter(data[labels == i, 0], data[labels == i, 1], c=colors[i], label=f'クラスター {i+1}')
plt.scatter(centroids[:, 0], centroids[:, 1], c='k', marker='x', s=100, label='中心座標')
plt.title('K-means クラスター')
plt.xlabel('説明変数 1')
plt.ylabel('説明変数 2')
plt.legend()
plt.show()
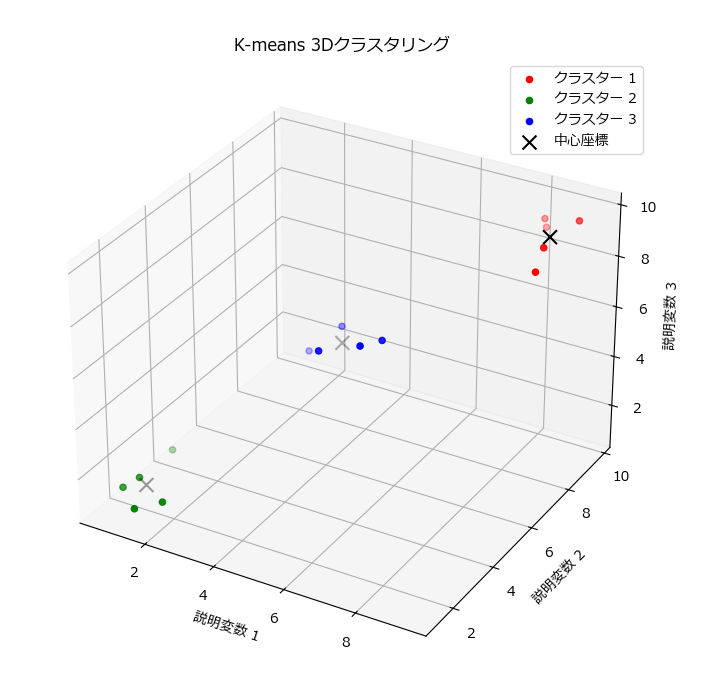
3次元データのクラスタリング結果を可視化
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
# 3次元データを15個生成
data = [
[1.0, 2.0, 1.5], [1.2, 3.2, 1.8], [1.8, 1.8, 1.0], [1.3, 1.3, 0.9], [0.7, 1.7, 1.2],
[5.0, 6.0, 5.5], [4.3, 6.3, 5.8], [3.7, 5.7, 5.0], [5.4, 6.4, 5.6], [4.1, 5.5, 5.3],
[9.0, 8.0, 9.5], [9.3, 9.3, 9.8], [8.2, 9.7, 8.9], [9.1, 7.4, 9.0], [8.2, 9.6, 9.3]
]
# K-meansクラスタリングの実行
kmeans = KMeans(n_clusters=3)
kmeans.fit(data)
# クラスタリング結果の取得
labels = kmeans.labels_
centroids = kmeans.cluster_centers_
# クラスタリング結果の可視化
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
colors = ['r', 'g', 'b']
for i in range(3):
ax.scatter(data[labels == i, 0], data[labels == i, 1], data[labels == i, 2], c=colors[i], label=f'クラスター {i+1}')
ax.scatter(centroids[:, 0], centroids[:, 1], centroids[:, 2], c='k', marker='x', s=100, label='中心座標')
ax.set_title('K-means 3Dクラスタリング')
ax.set_xlabel('説明変数 1')
ax.set_ylabel('説明変数 2')
ax.set_zlabel('説明変数 3')
ax.legend()
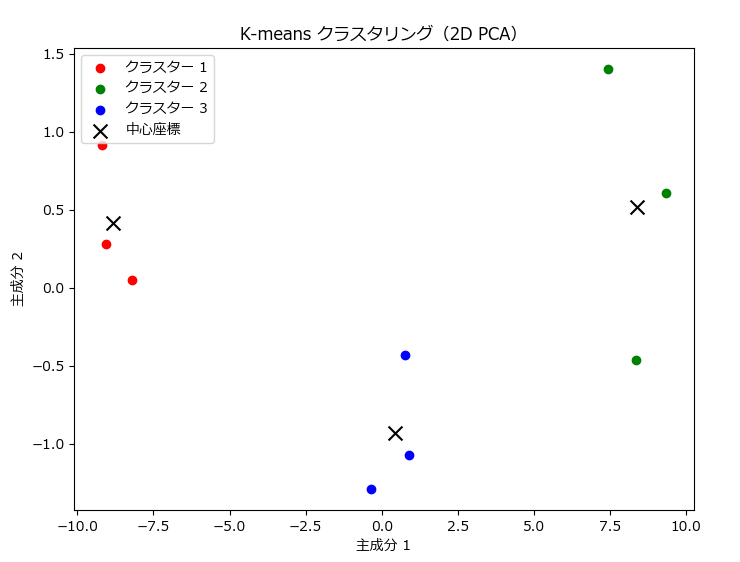
plt.show()多次元データを次元圧縮し、クラスタリング結果を可視化
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
# 6次元データの生成
data = [
[1.0, 2.0, 1.5, 3.2, 2.1, 0.8], [1.2, 3.2, 1.8, 3.5, 2.2, 0.9], [1.8, 1.8, 1.0, 3.0, 2.0, 0.7],
[5.0, 6.0, 5.5, 6.2, 6.1, 5.8], [4.3, 6.3, 5.8, 6.5, 6.2, 5.9], [3.7, 5.7, 5.0, 6.0, 5.9, 5.6],
[9.0, 8.0, 9.5, 8.2, 8.1, 7.8], [9.3, 9.3, 9.8, 9.5, 8.9, 8.7], [8.2, 9.7, 8.9, 9.0, 8.8, 8.6]
]
# --------------------------------------------------------------------------------------
# PCAを使って6次元データを2次元に変換してからクラスタリングを実行
# --------------------------------------------------------------------------------------
# PCAによる次元削減(2次元)
pca_2d = PCA(n_components=2)
data_2d = pca_2d.fit_transform(data)
# K-meansクラスタリングの実行(2次元)
kmeans_2d = KMeans(n_clusters=3)
kmeans_2d.fit(data_2d)
labels_2d = kmeans_2d.labels_
centroids_2d = kmeans_2d.cluster_centers_
# 2次元クラスタリング結果の可視化
plt.figure(figsize=(8, 6))
colors = ['r', 'g', 'b']
for i in range(3):
plt.scatter(data_2d[labels_2d == i, 0], data_2d[labels_2d == i, 1], c=colors[i], label=f'クラスター {i+1}')
plt.scatter(centroids_2d[:, 0], centroids_2d[:, 1], c='k', marker='x', s=100, label='中心座標')
plt.title('K-means クラスタリング(2D PCA)')
plt.xlabel('主成分 1')
plt.ylabel('主成分 2')
plt.legend()
plt.show()
# --------------------------------------------------------------------------------------
# PCAを使って6次元データを3次元に変換してからクラスタリングを実行
# --------------------------------------------------------------------------------------
# PCAによる次元削減(3次元)
pca_3d = PCA(n_components=3)
data_3d = pca_3d.fit_transform(data)
# K-meansクラスタリングの実行(3次元)
kmeans_3d = KMeans(n_clusters=3)
kmeans_3d.fit(data_3d)
labels_3d = kmeans_3d.labels_
centroids_3d = kmeans_3d.cluster_centers_
# 3次元クラスタリング結果の可視化
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
for i in range(3):
ax.scatter(data_3d[labels_3d == i, 0], data_3d[labels_3d == i, 1], data_3d[labels_3d == i, 2], c=colors[i], label=f'クラスター {i+1}')
ax.scatter(centroids_3d[:, 0], centroids_3d[:, 1], centroids_3d[:, 2], c='k', marker='x', s=100, label='中心座標')
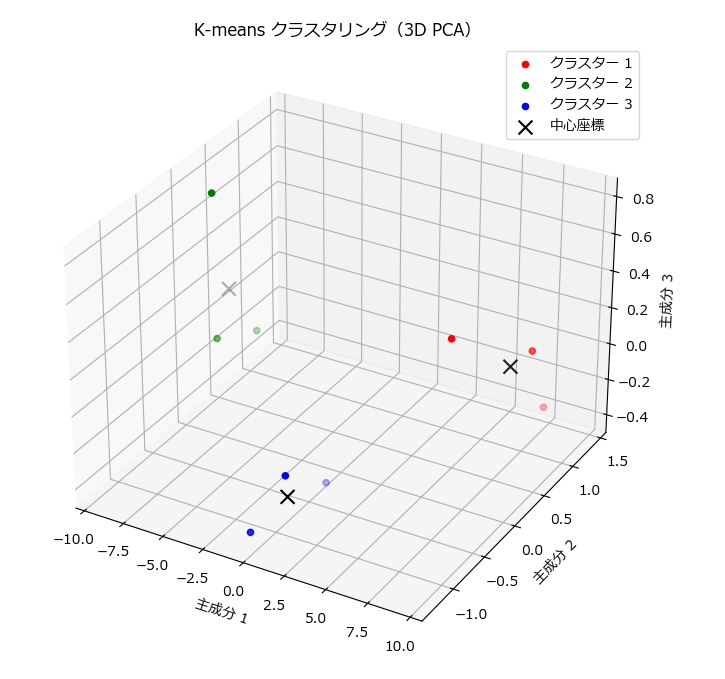
ax.set_title('K-means クラスタリング(3D PCA)')
ax.set_xlabel('主成分 1')
ax.set_ylabel('主成分 2')
ax.set_zlabel('主成分 3')
ax.legend()
plt.show()製造業向けのクラスタリング自作クラス
Kmeans を手軽に実行するための KmeansUtilクラスです。
DataFrameとしてデータを用意し、クラスタリングしたいカラムをリストで指定するだけで、クラスタリングが行えます。
また、クラスタリングの際、分類ルールが自動的に生成されるため、これをモデルファイルとして保存したり、ファイルからモデルを読み出して別のデータに適用することも可能です。
また、KmeansUtilクラスのインスタンスを渡すと、グラフを描画する関数も用意しました。
2次元のグラフは plot_clusters()、3次元のグラフは plot_clusters_3d()を使います。
自作クラスの使い方
- クラスタリングしたい対象データをDataFrameに格納し、
KmeansUtilの引数にDataFrameを指定してインスタンスを生成します。 fit()メソッドの引数にカラム名のリスト(columns)と分割数(n_clusters)を指定して呼び出します。- インスタンス作成時ではなく、
fit()の引数にDataFrameを指定することも可能です。 - クラスタリングした結果は
labelsとcentersのプロパティから取得可能です。 - クラスタリングにより生成された分類ルールは、
save_model()メソッドでファイルに保存できます。
# データの生成
df = pd.DataFrame([
[1.0, 2.0, 1.5], [1.2, 3.2, 1.8], [1.8, 1.8, 1.0], [1.3, 1.3, 0.9], [0.7, 1.7, 1.2],
[5.0, 6.0, 5.5], [4.3, 6.3, 5.8], [3.7, 5.7, 5.0], [5.4, 6.4, 5.6], [4.1, 5.5, 5.3],
[9.0, 8.0, 9.5], [9.3, 9.3, 9.8], [8.2, 9.7, 8.9], [9.1, 7.4, 9.0], [8.2, 9.6, 9.3]
], columns=['Feature1', 'Feature2','Feature3'])
# モデル作成~モデル保存まで
dbs = KmeansUtil(df)
dbs.fit(['Feature1', 'Feature2','Feature3'], n_clusters=3)
dbs.save_model("./kmeans")
# 結果を表示
print(dbs.labels)
plot_clusters_3d(dbs)- モデルファイルとして保存した分類ルールを別のデータに適用するには、モデルファイルのパスを引数に指定して
KmeansUtilインスタンス生成します。 - インスタンス生成時ではなく、
load_model()メソッドを使ってモデルファイルを読み出すことも可能です。 - クラスタリングしたいデータを格納したDataFrameと、カラムのリストを指定して
predict()メソッドを呼び出します。 - クラスタリングした結果は
labelsとcentersのプロパティから取得可能です。
# データを生成
df = pd.DataFrame([
[1.1, 2.1, 2.5], [2.2, 4.3, 2.3], [1.5, 1.6, 1.2], [1.5, 1.4, 0.8], [1.7, 2.7, 3.5],
[5.1, 6.2, 4.5], [3.3, 5.4, 6.8], [3.2, 6.1, 5.3], [5.5, 6.4, 5.5], [4.5, 3.4, 4.2],
[9.1, 8.5, 7.5], [8.3, 9.2, 9.1], [8.3, 9.4, 9.9], [9.3, 7.3, 9.1], [8.1, 9.2, 9.4]
], columns=['Feature1', 'Feature2','Feature3'])
# モデル読み込み~クラスタリングまで
km = KmeansUtil(model_path="./kmeans")
km.predict(['Feature1', 'Feature2','Feature3'],df=df)
# 結果を表示
print(km.centers)
print(km.labels)
plot_clusters_3d(km)Kmeansユーティリティクラス
| メソッド名 | 説明 | パラメータ | 戻り値 |
|---|---|---|---|
| __init__( df, model_path, pca = 0 ) | クラスの初期化 | df: データフレーム model_path: モデルファイルパス pca: PCA次元数 | なし |
| fit( cloumns, df=None, kmeans_paramms ) | KMeansモデルの学習 | columns: 使用するカラム df: データフレーム kmeans_params: KMeansのパラメータ | 学習済みのKMeansモデル |
| predict( columns=None, df=None ) | 新しいデータに対する予測 | columns: 使用するカラム df: データフレーム | 予測ラベル |
| read_csv( file_name, encoding="shift-jis" ) | CSVファイルからデータを読み込む | file_name: ファイルパス encoding: エンコーディング | なし |
| save_model( model_path ) | 学習したモデルを保存する | model_path: 保存ファイルパス | なし |
| load_model( model_path=None ): | 保存したモデルを読み込む | model_path: 読み込みファイルパス | 読み込んだモデル |
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
import pickle
class KmeansUtil:
def __init__(self, df=None, model_path=None, pca=0):
"""
KMeansUtilクラスの初期化メソッド
:param df: 初期データフレーム (pd.DataFrame)
:param model_path: モデルファイルのパス (str)
:param pca: PCAを適用する次元数 (0: 使用しない, 2: 2次元, 3: 3次元)
"""
self.df = None if df is None else df.copy() # データフレームのコピーを保持
self.model = None if model_path is None else self.load_model(model_path) # モデルファイルのパス
self.labels = []
self.centers = []
self.columns = []
self.pca = pca # PCA次元数の指定
def fit(self, columns: list, df: pd.DataFrame = None, **kmeans_params):
if df is not None:
self.df = df
self.columns = columns
X = self.df[columns].values
if self.pca > 0:
# PCAによる次元削減
pca_model = PCA(n_components=self.pca)
X = pca_model.fit_transform(X)
# KMeansモデルを作成
self.model = KMeans(**kmeans_params)
self.model.fit(X) # クラスタリングを実行
self.labels = self.model.labels_ # ラベルを取得
self.centers = self.model.cluster_centers_ # クラスタ中心を取得
# PCA逆変換で元の空間に戻す
if self.pca > 0:
self.centers = pca_model.inverse_transform(self.centers)
return self.model
def predict(self, columns=None, df=None):
if df is not None:
self.df = df
if columns is not None:
self.columns = columns
X = self.df[self.columns].values
if self.pca > 0:
# PCAによる次元削減
pca_model = PCA(n_components=self.pca)
X = pca_model.fit_transform(X)
self.labels = self.model.predict(X) # 予測結果
self.centers = self.model.cluster_centers_ # 更新されたクラスタ中心
# PCA逆変換で元の空間に戻す
if self.pca > 0:
self.centers = pca_model.inverse_transform(self.centers)
return self.labels
def read_csv(self, file_name, encoding="shift-jis"):
"""
CSVファイルからデータを読み込むメソッド
:param file_name: 読み込むファイルのパス (str)
:param encoding: ファイルのエンコーディング (str)
"""
self.df = pd.read_csv(file_name, encoding=encoding) # データフレームに読み込み
def save_model(self, model_path):
"""
学習したモデルをファイルに保存するメソッド
:param model_path: 保存するファイルのパス (str)
"""
with open(model_path, 'wb') as f:
pickle.dump(self.model, f) # モデルをバイナリ形式で保存
def load_model(self, model_path=None):
"""
モデルをファイルから読み込むメソッド
:param model_path: 読み込むファイルのパス (str)
:return: 読み込んだモデル
"""
if model_path is None:
model_path = self.model_path
with open(model_path, 'rb') as f:
self.model = pickle.load(f) # モデルをバイナリ形式で読み込み
return self.modelグラフ描画関数
| 関数名 | 説明 | 引数 | 戻り値 | 備考 |
|---|---|---|---|---|
| plot_clusters( kmeans_util, x_col=None, y_col=None ) | 2次元クラスタリングの結果を可視化する関数です。クラスタの中心と各データ点をプロットします。 | kmeans_util: KMeansUtilのインスタンス x_col: x軸にプロットするカラム名 y_col: y軸にプロットするカラム名 | None | x_col, y_colが指定されない場合は、KmeansUtil.columnsの最初の2つが使用されます。 |
| plot_clusters_3d( kmeans_util, x_col=None, y_col=None, z_col=None ) | 3次元クラスタリングの結果を可視化する関数です。クラスタの中心と各データ点をプロットします。 | kmeans_util: KMeansUtilのインスタンス x_col: x軸にプロットするカラム名 y_col: y軸にプロットするカラム名 z_col: z軸にプロットするカラム名 | None | x_col, y_col, z_colが指定されない場合は、KmeansUtil.columnsの最初の3つが使用されます。 |
下記は2次元グラフの描画関数です。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
def plot_clusters(kmeans_util, x_col=None, y_col=None):
"""
クラスタリング結果を可視化
- kmeans_util: KMeansUtilのインスタンス
- x_col, y_col: プロットするカラム名(省略時にはkmeans_util.columnsを使用)
"""
if not isinstance(kmeans_util, KmeansUtil):
raise ValueError("引数はKMeansUtilのインスタンスでなければなりません。")
# x_col, y_colが指定されていない場合、kmeans_util.columnsを使用
if x_col is None or y_col is None:
if len(kmeans_util.columns) < 2:
raise ValueError("x_col と y_col が指定されていない場合、columnsに2つ以上のカラムが必要です。")
x_col = kmeans_util.columns[0] # columnsの1番目をx軸
y_col = kmeans_util.columns[1] # columnsの2番目をy軸
# クラスタリングラベルがない場合、予測を実行
if len(kmeans_util.labels) == 0:
kmeans_util.predict()
plt.figure(figsize=(8, 6))
# クラスタごとにデータポイントをプロット
for cluster in np.unique(kmeans_util.labels):
cluster_data = kmeans_util.df[kmeans_util.labels == cluster]
plt.scatter(cluster_data[x_col], cluster_data[y_col], label=f"クラスター {cluster}")
# クラスタの中心を1回だけプロット(凡例は一度だけ表示)
plt.scatter(kmeans_util.centers[:, 0], kmeans_util.centers[:, 1], c='red', marker='x', s=100, label='中心座標')
plt.xlabel(x_col)
plt.ylabel(y_col)
plt.legend()
plt.title("Cluster Visualization with Centers")
plt.show()
下記は3次元グラフの描画関数です。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
def plot_clusters_3d(kmeans_util, x_col=None, y_col=None, z_col=None):
"""
3Dクラスタリング結果を可視化
- kmeans_util: KMeansUtilのインスタンス
- x_col, y_col, z_col: プロットするカラム名(省略時にはkmeans_util.columnsを使用)
"""
if not isinstance(kmeans_util, KmeansUtil):
raise ValueError("引数はKMeansUtilのインスタンスでなければなりません。")
# x_col, y_col, z_colが指定されていない場合、kmeans_util.columnsを使用
if x_col is None or y_col is None or z_col is None:
if len(kmeans_util.columns) < 3:
raise ValueError("x_col, y_col, z_col が指定されていない場合、columnsに3つ以上のカラムが必要です。")
x_col = kmeans_util.columns[0] # columnsの1番目をx軸
y_col = kmeans_util.columns[1] # columnsの2番目をy軸
z_col = kmeans_util.columns[2] # columnsの3番目をz軸
# クラスタリングラベルがない場合、予測を実行
if len(kmeans_util.labels) == 0:
kmeans_util.predict()
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
# クラスタごとにデータポイントをプロット
for cluster in np.unique(kmeans_util.labels):
cluster_data = kmeans_util.df[kmeans_util.labels == cluster]
ax.scatter(cluster_data[x_col], cluster_data[y_col], cluster_data[z_col], label=f"クラスター {cluster}")
# クラスタの中心を1回だけプロット(凡例は一度だけ表示)
ax.scatter(kmeans_util.centers[:, 0], kmeans_util.centers[:, 1], kmeans_util.centers[:, 2], c='red', marker='x', s=100, label='中心座標')
ax.set_xlabel(x_col)
ax.set_ylabel(y_col)
ax.set_zlabel(z_col)
ax.legend()
ax.set_title("3D Cluster Visualization with Centers")
plt.show()まとめ
k-means法は、機械学習やデータ分析の分野で広く利用されているクラスタリング手法です。
本記事では、Pythonを用いたk-meansの実装方法を解説しました。
データをグループ分けして、それぞれの特徴や傾向を明確にすることで、データの内容をより詳しく理解することができます。
ただし、次元数が多い場合は次元削減を行う必要がある点に注意が必要です。
k-meansを活用することで、データ分析の幅が広がり、新たな発見や気づきを得る手助けとなれば幸いです。









コメント