械学習のアルゴリズムは数多くありますが、「精度の高いモデルを簡単に構築したい!」そんなときに頼れるのが ランダムフォレスト(Random Forest) です。
本記事では、分類問題と回帰問題の両方にランダムフォレストを活用する方法を、サンプルコード付きでわかりやすく解説します。
Pythonでの実装方法はもちろん、決定木との違いや、メリット・デメリット、パラメータチューニングのポイントまで幅広く網羅していますので、ランダムフォレストを使ってみたいという方は、是非ご一読ください。
ランダムフォレストとは
ランダムフォレスト (Random Forest) は、機械学習のアルゴリズムの1つで、分類や回帰の問題を解決するために使用されます。多くの決定木 (Decision Trees) を組み合わせて、全体の予測精度を向上させるアンサンブル学習手法の1つです。特に、ノイズの多いデータや非線形な関係を持つデータに対して優れた性能を発揮します。

ランダムフォレストの仕組み
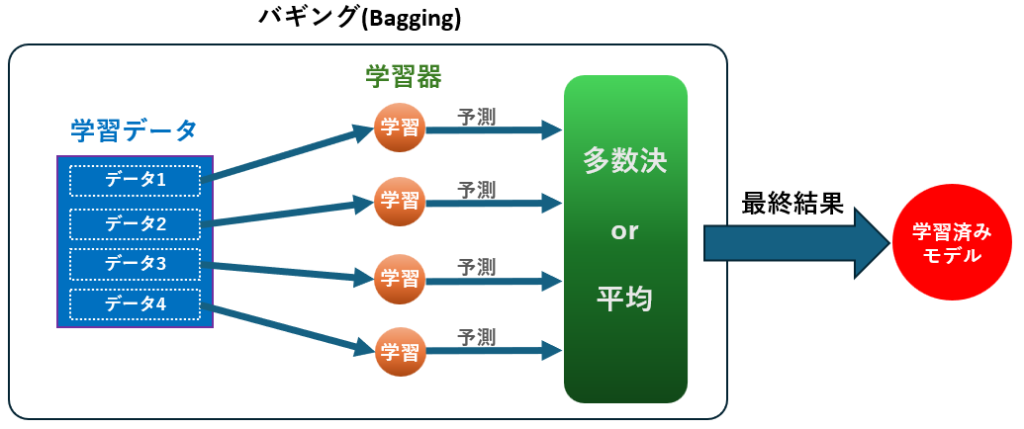
ランダムフォレストは以下の手順で構築されます:
- データのサンプリング:
元のデータセットからブートストラップ法を用いて複数のサブセットをランダムに抽出します。 - 決定木の構築:
各サブセットに対して、異なる特徴量のサブセットを用いながら決定木を構築します。これにより、個々の決定木が異なる視点から学習を行います。 - 予測の統合:
すべての決定木の結果を集約します。分類の場合は「多数決」で最終的なクラスを決定し、回帰の場合は「平均値」を計算して予測値を求めます。
これにより、1つの決定木が持つ過学習やバイアスの問題を軽減し、頑健なモデルを構築することができます。
さらに詳しい情報は、スタッツギルド株式会社のこちらの記事が参考になります。
決定木との違い
ランダムフォレストは複数の決定木を利用するため、過学習を防ぎつつ高い精度を実現する点で決定木よりも優れています。一方で、学習や予測にかかる計算コストは決定木よりも高くなる場合があります。
| 特徴 | 決定木 | ランダムフォレスト |
|---|---|---|
| 構造 | 1本の木 | 複数の木 |
| 過学習のしやすさ | 高い | 低い |
| 学習速度 | 速い | 遅い |
| 精度 | 単純なデータでは高い | 複雑なデータで高い |
| 特徴量選択 | 全特徴量を使用 | 一部の特徴量をランダムに使用 |
ランダムフォレストのメリット・デメリット
メリット
- 高い汎化性能: 過学習を抑えつつ、安定した予測が可能。
- 非線形データへの対応: データの分布や関係が複雑でも高い精度を発揮。
- 特徴量の重要度評価: 各特徴量が予測にどの程度寄与しているかを計算できる。
- 欠損値の耐性: 一部のデータが欠損していても精度が大きく低下しにくい。
デメリット
- 計算コストが高い: 複数の決定木を構築するため、計算リソースを多く消費する。
- ブラックボックス化: 個々の決定木の判断基準が分かりにくく、結果の解釈が難しい。
- データセットの依存度: 高次元データや特徴量の数が多すぎる場合、パフォーマンスが低下することがある。
ランダムフォレストに適したデータ
ランダムフォレストは、以下のようなデータに適しています
- 多次元で複雑なデータ: 特徴量が多いデータでも、重要な特徴量を選択しながら学習が行える。
- ノイズが多いデータ: 個々の決定木が異なる特徴量やデータサブセットを学習するため、ノイズの影響に強い。
- 非線形な関係を持つデータ: 線形モデルでは捉えにくい複雑なパターンを検出できる。
- 少量の欠損値を含むデータ: 欠損値があっても精度が大きく低下しにくいため、実用的。
逆に、以下のようなデータには適さない場合があります
- 非常に高次元かつ特徴量がスパースなデータ(例: テキストデータ)。
- リアルタイム性が求められる用途(計算コストが高いため)。
製造業におけるランダムフォレストの用途
製造業において、ランダムフォレストは次の用途で使われています。
| 用途 | 概要 | タイプ | 例 |
|---|---|---|---|
| 異常検知 | 製品や設備のセンサーから得られるデータを分析し、異常なパターンを検出 | 分類 | 振動データを基にした機械の故障予測 |
| 品質予測 | 製造プロセス中のパラメータと品質データを関連付け、不良品の発生を予測 | 回帰 | 温度や圧力などのプロセス変数を基にした製品品質の推定 |
| 需要予測 | 過去の生産データや販売データを基に、需要の変動を予測 | 回帰 | 季節性やトレンドを考慮した在庫管理 |
| 故障分類 | 設備のセンサー値やログデータから、故障の種類を特定 | 分類 | 異常が発生した際に、電気系の問題か機械的な問題かを分類 |
| 生産量最適化 | 生産プロセスを最適化するために、最適な生産条件を予測 | 回帰 | 材料投入量と加工時間から、最大効率を達成する条件を予測 |
| エネルギー消費予測 | 工場全体や特定の設備でのエネルギー消費を予測し、効率化に役立てる | 回帰 | 過去の使用データを基にしたピーク時のエネルギー消費量の推定 |
ランダムフォレストによる分類問題の解き方
事前準備(ライブラリ導入とデータ準備)
事前に下記3つのライブラリをインストールしてください。
pip install matplotlib
pip install pandas
pip install scikit-learn
下記は今回の分類に使うダミーデータの生成プログラムです。4種類に分類可能な特徴量_1~7のデータとなります。
機械の異常検知の場合はセンサー値、不良予測の場合は設備や材料に関する情報に読み替えて下さい。
from sklearn.datasets import make_classification
import pandas as pd
# ダミーデータ作成
X, y = make_classification(
n_samples=1000, # サンプル数
n_features=7, # 特徴量数
n_informative=5, # 有効な特徴量数
n_redundant=2, # 冗長な特徴量数
n_classes=4, # クラス数
n_clusters_per_class=1, # クラス内のクラスター数
flip_y=0.05, # ノイズの割合
random_state=42
)
# データフレーム化
df = pd.DataFrame(X, columns=[f"特徴量_{i+1}" for i in range(7)])
df['正解データ'] = y
# ファイルに保存
df.to_csv("classification_data.csv", index=False)特徴量_1~7は下記の通り、一見何の特徴もありませんが、目的変数は綺麗に4つに分かれています。
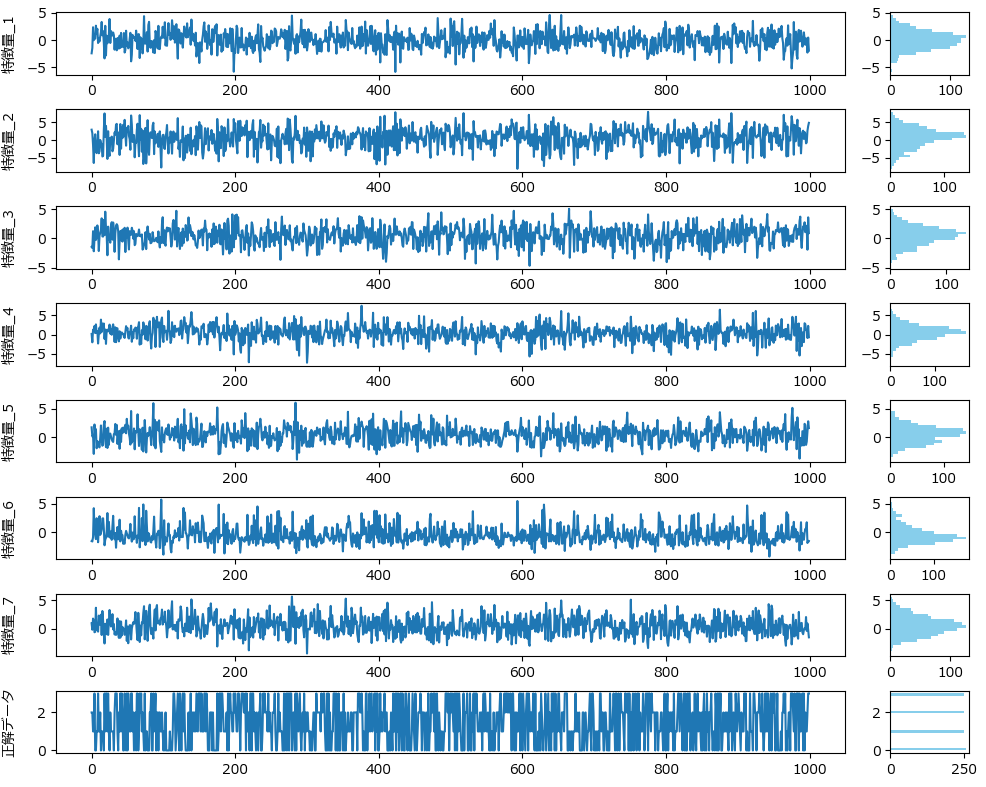
ランダムフォレストを用いた分類モデルの学習と評価(サンプルコードと解説)
以下は、ランダムフォレストを用いて分類モデルの学習と評価を行うサンプルコードです。
このまま実行すると学習が始まり、精度評価指標(混同行列、accuracyなど)が出力されます。
学習と評価の部分は、train_random_forest_classifierという名前で関数化していますので、コピペでお使いいただけます。
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, classification_report
from sklearn.metrics import confusion_matrix
def train_random_forest_classifier(df, target, columns, params={}, test_size=0.2, random_state=42):
"""
指定されたデータフレームとパラメータに基づいてランダムフォレストを学習させ、レポートを出力する関数。
引数:
df : pandas.DataFrame
データを含むデータフレーム。
target : str
予測対象となるターゲット列名。
columns : list of str
使用する特徴量の列名のリスト。Targetが含まれていても無視する。
params : dict, optional (default={})
ランダムフォレストのハイパーパラメータ。
test_size : float, optional (default=0.2)
テストデータの割合。
random_state : int, optional (default=42)
乱数シード。
戻り値:
model : RandomForestClassifier
訓練されたランダムフォレスト分類器のモデルオブジェクト。
cm : numpy.ndarray
混同行列を表す2次元配列。
"""
# 特徴量とターゲットに分ける(target 列を除外)
columns = [col for col in columns if col != target]
X = df[columns]
y = df[target]
# 訓練データとテストデータに分割する
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state)
# ランダムフォレスト分類器のインスタンスを作成する
model = RandomForestClassifier(random_state=random_state, **params)
# モデルを訓練する
model.fit(X_train, y_train)
# テストデータで予測する
y_pred = model.predict(X_test)
# モデルの精度を評価する
accuracy = accuracy_score(y_test, y_pred)
report = classification_report(y_test, y_pred, target_names=[str(i) for i in range(len(df[target].unique()))])
cm = confusion_matrix(y_test, y_pred)
print(f'正解率: {accuracy}')
print('混同行列:')
print(cm)
print('分類レポート:')
print(report)
return model, cm
if __name__ == "__main__":
# データを読み込む
df = pd.read_csv('classification_data.csv')
# 関数の呼び出し(ハイパーパラメータはデフォルト値を使用)
model, cm = train_random_forest_classifier(df, target='正解データ', columns=df.columns)
# クラス名を設定して混同行列をプロット
class_names = df['正解データ'].unique().astype(str)正解率: 0.925
混同行列:
[[44 1 1 5]
[ 0 46 0 0]
[ 1 0 50 2]
[ 0 3 2 45]]
分類レポート:
precision recall f1-score support
0 0.98 0.86 0.92 51
1 0.92 1.00 0.96 46
2 0.94 0.94 0.94 53
3 0.87 0.90 0.88 50
accuracy 0.93 200
macro avg 0.93 0.93 0.93 200
weighted avg 0.93 0.93 0.92 200
ハイパーパラメータを指定する場合は、paramsに辞書形式で指定します。必要に応じて適宜値を書き換え、実行してください。
# 関数の呼び出し(ハイパーパラメータを指定)
train_random_forest_classifier(df, target='正解データ', columns=df.columns,params={'n_estimators': 100})分類結果(混同行列)の視覚化
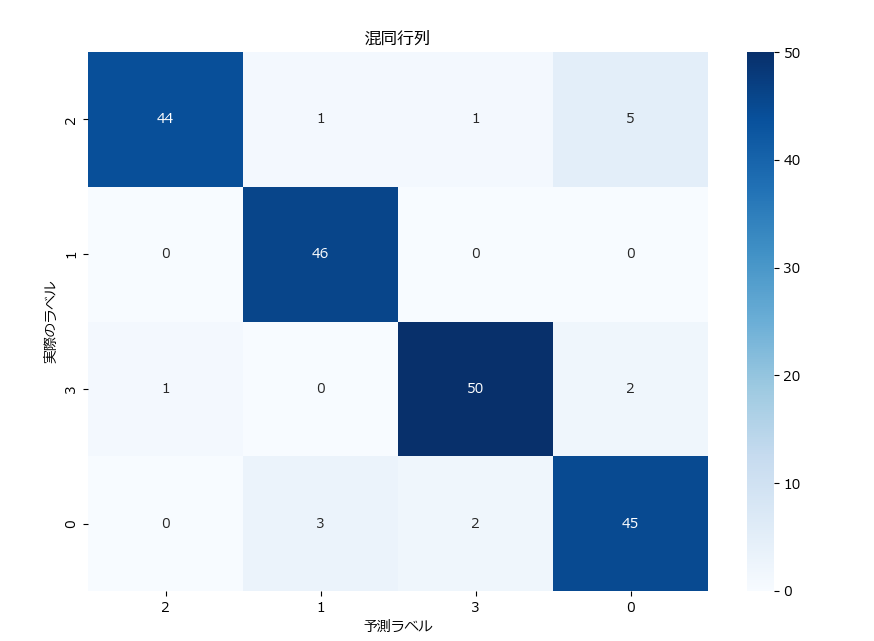
混同行列を可視化すると、結果が直感的に分かり易くなります。下記がそのサンプルです。 plot_confusion_matrixという関数名にしていますので、コピペで利用可能です。
#---------------------------------------------------------------
# この部分に、前述した train_random_forest_classifier関数 を張り付けて下さい
#---------------------------------------------------------------
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
def plot_confusion_matrix(cm, class_names=[]):
"""
混同行列をプロットする関数。
引数:
cm : numpy.ndarray
混同行列を表す2次元配列。
class_names : list of str, optional
クラス名のリスト。省略すると連番が表示される
"""
plt.figure(figsize=(10, 7))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues', xticklabels=class_names, yticklabels=class_names)
plt.xlabel('予測ラベル')
plt.ylabel('実際のラベル')
plt.title('混同行列')
plt.show()
if __name__ == "__main__":
# データを読み込む
df = pd.read_csv('classification_data.csv')
# 関数の呼び出し(ハイパーパラメータはデフォルト値を使用)
model, cm = train_random_forest_classifier(df, target='正解データ', columns=df.columns)
# クラス名を設定して混同行列をプロット
class_names = df['正解データ'].unique().astype(str)
plot_confusion_matrix(cm, class_names=class_names)分類結果の評価
今回のテストデータに対してランダムフォレストで分類した結果を整理し、評価してみました。
正解率
| 正解率(Accuracy) | 0.925 |
|---|
モデルの全体的な精度は非常に高いと言えます。
混同行列
| 正解の分類クラス | クラス 0の予測件数 | クラス 1の予測件数 | クラス 2の予測件数 | クラス 3の予測件数 |
|---|---|---|---|---|
| クラス 0 | 44 | 1 | 1 | 5 |
| クラス 1 | 0 | 46 | 0 | 0 |
| クラス 2 | 1 | 0 | 50 | 2 |
| クラス 3 | 0 | 3 | 2 | 45 |
クラス0は誤分類が7件、クラス1は誤分類が0件、クラス2は誤分類が3件、クラス3は誤分類が5件であるため、高い精度で分類されていることが分かります。
分類レポート
| クラス | 適合率 (Precision) | 再現率 (Recall) | F1スコア (F1-Score) | サポート (Support) |
|---|---|---|---|---|
| 0 | 0.98 | 0.86 | 0.92 | 51 |
| 1 | 0.92 | 1.00 | 0.96 | 46 |
| 2 | 0.94 | 0.94 | 0.94 | 53 |
| 3 | 0.87 | 0.90 | 0.88 | 50 |
| 指標 | 適合率 (Precision) | 再現率 (Recall) | F1スコア (F1-Score) | サンプル数 |
|---|---|---|---|---|
| 正解率(Accuracy) | - | - | 0.93 | 200 |
| マクロ平均 | 0.93 | 0.93 | 0.93 | 200 |
| 加重平均 | 0.93 | 0.93 | 0.92 | 200 |
分類レポートから見ると、全体として非常に高い性能を示しています。
但し、クラス 3 の適合率と再現率も、他のクラスに比べてやや低いので、バランスよくパフォーマンスを向上させるための対策が考えられます。
また、クラス 0 に対する再現率が他のクラスより低いので、見逃しが若干多いことが懸念されます。クラス 0 のデータをさらに増やすか、モデルのハイパーパラメータを調整することで改善を試みることができます。
- クラス 0:
再現率が若干低めなので、実際のクラス 0 を見逃す可能性があります。 - クラス 1:
再現率が 1.00 であり、実際のクラス 1 を全く見逃していないことを示します。 - クラス 2:
バランスが取れており、適合率と再現率の両方が高いです。 - クラス 3:
適合率と再現率がやや低いですが、全体としては良好なパフォーマンスです。 - マクロ平均:
モデルが全てのクラスで安定した性能を示していることを確認できます。 - 加重平均:
サンプル数の多いクラスがモデル評価に与える影響を考慮しています。
ランダムフォレストによる回帰問題の解き方
事前準備(ライブラリ導入とデータ準備)
事前に下記3つのライブラリをインストールしてください。
pip install matplotlib
pip install pandas
pip install scikit-learn
下記は今回の回帰に使うダミーデータの生成プログラムです。7つの特徴量のデータとなります。
import numpy as np
import pandas as pd
# 特徴量の数
n_features = 7
# 各特徴量の標準偏差
std_devs = [1, 1, 1, 1, 1, 1, 1]
# 相関行列の設定(例: 1番目と2番目の特徴量が強い相関を持つ)
correlation_matrix = np.array([
[1, 0.8, 0.2, 0.1, 0.1, 0.1, 0.1],
[0.8, 1, 0.3, 0.2, 0.2, 0.2, 0.2],
[0.2, 0.3, 1, 0.4, 0.3, 0.3, 0.3],
[0.1, 0.2, 0.4, 1, 0.5, 0.5, 0.5],
[0.1, 0.2, 0.3, 0.5, 1, 0.4, 0.4],
[0.1, 0.2, 0.3, 0.5, 0.4, 1, 0.3],
[0.1, 0.2, 0.3, 0.5, 0.4, 0.3, 1]
])
# 共分散行列の計算
covariance_matrix = np.outer(std_devs, std_devs) * correlation_matrix
# ダミーデータの生成
np.random.seed(42)
n_samples = 1000
data = np.random.multivariate_normal(np.zeros(n_features), covariance_matrix, size=n_samples)
# DataFrameに変換
df = pd.DataFrame(data, columns=[f'特徴量_{i+1}' for i in range(n_features)])
# 結果の確認
print(df.head())
# CSVファイルに保存
df.to_csv('regression_data.csv', index=False)下記のグラフは、分類モデル用データ生成で紹介したplot_features_with_histogramを使って描画しました。
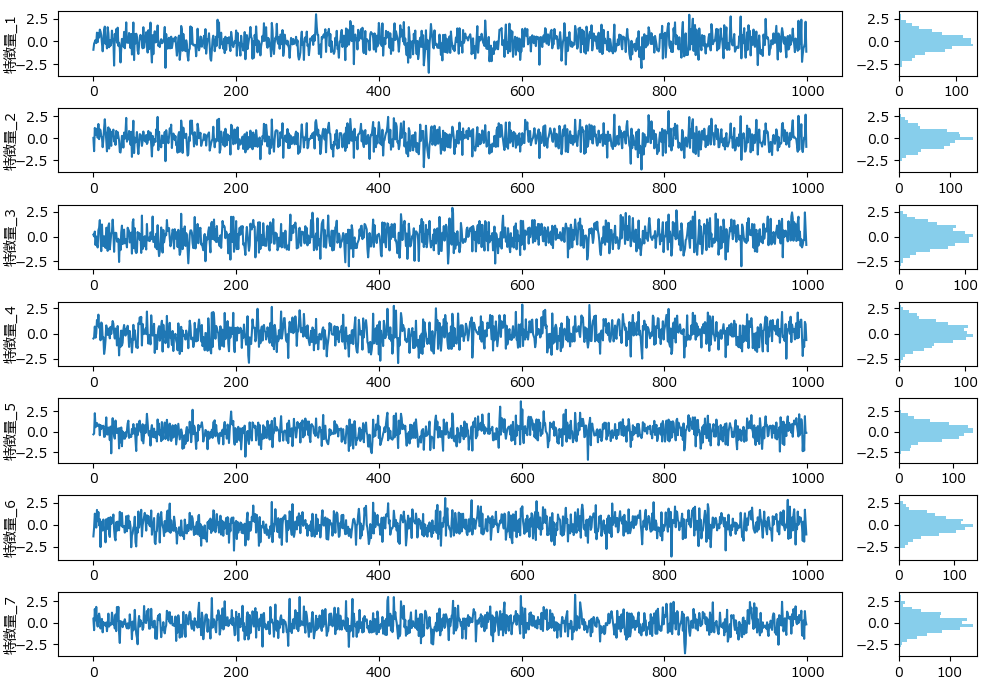
ランダムフォレストによる回帰モデルの学習と評価(サンプルコードと解説)
以下は、ランダムフォレストを用いて回帰モデルの学習と評価を行うサンプルコードです。
このまま実行すると学習が始まり、精度評価指標(統計情報、平均絶対誤差、平均二乗誤差、重要度など)が出力されます。
学習と評価の部分は、train_random_forest_regressorという名前で関数化していますので、コピペでお使いいただけます。
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score, mean_absolute_percentage_error
def train_random_forest_regressor(df, target, columns, params={}, test_size=0.2, random_state=42):
"""
指定されたデータフレームとパラメータに基づいてランダムフォレスト回帰モデルを学習させ、レポートを出力する関数。
引数:
df : pandas.DataFrame
データを含むデータフレーム。
target : str
予測対象となるターゲット列名。
columns : list of str
使用する特徴量の列名のリスト。ターゲットが含まれていても無視する。
params : dict, optional (default={})
ランダムフォレストのハイパーパラメータ。
test_size : float, optional (default=0.2)
テストデータの割合。
random_state : int, optional (default=42)
乱数シード。
戻り値:
model : RandomForestRegressor
訓練されたランダムフォレスト回帰モデルのオブジェクト。
y_test : list
テストに使った正解データ。
y_pred: list
予測した結果。
"""
# 特徴量とターゲットに分ける(target 列を除外)
columns = [col for col in columns if col != target]
X = df[columns]
y = df[target]
# 訓練データとテストデータに分割する
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state)
# ランダムフォレスト回帰モデルのインスタンスを作成する
model = RandomForestRegressor(random_state=random_state, **params)
# モデルを訓練する
model.fit(X_train, y_train)
# テストデータで予測する
y_pred = model.predict(X_test)
# モデルの精度を評価する
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse) # RMSE
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
mape = mean_absolute_percentage_error(y_test, y_pred)
# 統計情報を表示
print(f'{target}の統計情報:')
print(f'最小値(Min): {y.min()}')
print(f'最大値(Max): {y.max()}')
print(f'平均値(Mean): {y.mean()}')
print(f'標準偏差(Std): {y.std()}')
print(f'分散(Var): {y.var()}')
# 精度指標を出力する
print(f'平均絶対誤差 (Mean Absolute Error): {mae}')
print(f'平均二乗誤差 (Mean Squared Error): {mse}')
print(f'ルート平均二乗誤差 (Root Mean Squared Error): {rmse}')
print(f'平均絶対パーセンテージ誤差 (MAPE): {mape}')
print(f'決定係数 (R^2 Score): {r2}')
# 特徴量の重要度を表示する
feature_importances = model.feature_importances_
importance_df = pd.DataFrame({'特徴量 (Feature)': columns, '重要度 (Importance)': feature_importances})
importance_df = importance_df.sort_values(by='重要度 (Importance)', ascending=False)
print("\n特徴量の重要度:")
print(importance_df)
return model, y_test, y_pred
if __name__ == "__main__":
# データの読み込み
df = pd.read_csv('regression_data.csv')
# 特徴量_1 の予測モデルを作成する
model,y_test,y_pred = train_random_forest_regressor(df,'特徴量_1',df.columns)特徴量_1の統計情報:
最小値(Min): -3.4181790752853725
最大値(Max): 2.967258816333585
平均値(Mean): -0.018768452256335492
標準偏差(Std): 0.9893707041157269
分散(Var): 0.9788543901624494
平均絶対誤差 (Mean Absolute Error): 0.5039958639393453
平均二乗誤差 (Mean Squared Error): 0.3928372697417739
ルート平均二乗誤差 (Root Mean Squared Error): 0.6267673170657305
平均絶対パーセンテージ誤差 (MAPE): 2.2027217358416427
決定係数 (R^2 Score): 0.6529939477578449
特徴量の重要度:
特徴量 (Feature) 重要度 (Importance)
0 特徴量_2 0.705594
4 特徴量_6 0.066200
5 特徴量_7 0.061491
3 特徴量_5 0.056713
1 特徴量_3 0.056181
2 特徴量_4 0.053821
回帰結果の可視化
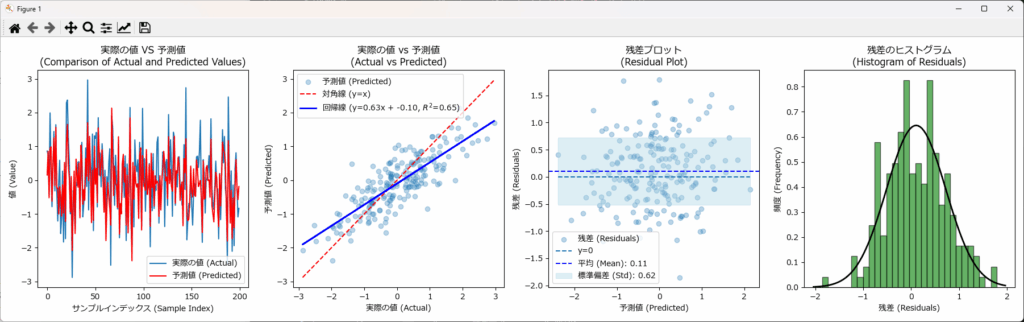
回帰結果を可視化することで、実際の値と予測値との差や、残差のバラつき具合、残差の分布状態が直感的に把握できます。下記がそのサンプルです。 plot_figuresという関数名にしていますので、コピペで利用可能です。
#------------------------------------------------------------------------
# この部分に、前述した train_random_forest_regressor 関数 を張り付けて下さい
#------------------------------------------------------------------------
from scipy.stats import norm
from sklearn.metrics import r2_score
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
def plot_figures(y_test, y_pred):
"""
グラフを描画し、指定されたファイル名で保存する関数
引数:
y_test : pandas.Series
実際の値
y_pred : numpy.ndarray
予測値
"""
# 残差の計算
residuals = y_test - y_pred
fig, axs = plt.subplots(1, 4, figsize=(18, 5))
# 実際の値と予測値の折れ線グラフ
axs[0].plot(y_test.values, label='実際の値 (Actual)', linestyle='-', marker=None)
axs[0].plot(y_pred, label='予測値 (Predicted)', color='red', linestyle='-', marker=None)
axs[0].set_xlabel('サンプルインデックス (Sample Index)')
axs[0].set_ylabel('値 (Value)')
axs[0].set_title('実際の値 VS 予測値\n(Comparison of Actual and Predicted Values)')
axs[0].legend()
# 実際の値と予測値の散布図
axs[1].scatter(y_test, y_pred, alpha=0.3, label='予測値 (Predicted)')
axs[1].plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', label='対角線 (y=x)')
# 回帰線の計算
slope, intercept = np.polyfit(y_test, y_pred, 1)
r2 = r2_score(y_test, y_pred)
axs[1].plot(y_test, slope * y_test + intercept, color='blue', linestyle='-', linewidth=2, label=f'回帰線 (y={slope:.2f}x + {intercept:.2f}, $R^2$={r2:.2f})')
axs[1].set_xlabel('実際の値 (Actual)')
axs[1].set_ylabel('予測値 (Predicted)')
axs[1].set_title('実際の値 vs 予測値\n(Actual vs Predicted)')
axs[1].legend()
# 残差プロット
axs[2].scatter(y_pred, residuals, alpha=0.3, label='残差 (Residuals)')
axs[2].hlines(y=0, xmin=y_pred.min(), xmax=y_pred.max(), linestyles='dashed', label='y=0')
# 残差の平均と標準偏差を計算
residuals_mean = np.mean(residuals)
residuals_std = np.std(residuals)
# y_pred をソートし、それに対応する範囲を再計算
sorted_indices = np.argsort(y_pred)
sorted_y_pred = y_pred[sorted_indices]
sorted_upper = residuals_mean + residuals_std
sorted_lower = residuals_mean - residuals_std
axs[2].axhline(y=residuals_mean, color='blue', linestyle='--', label=f'平均 (Mean): {residuals_mean:.2f}')
# 標準偏差の範囲を水色で塗りつぶし
axs[2].fill_between(
sorted_y_pred, # ソートされた予測値
sorted_lower, # 下限 (固定値)
sorted_upper, # 上限 (固定値)
color='lightblue',
alpha=0.4,
label=f'標準偏差 (Std): {residuals_std:.2f}'
)
axs[2].set_xlabel('予測値 (Predicted)')
axs[2].set_ylabel('残差 (Residuals)')
axs[2].set_title('残差プロット\n(Residual Plot)')
axs[2].legend()
# 残差のヒストグラム
axs[3].hist(residuals, bins=30, edgecolor='k', density=True, alpha=0.6, color='g')
# 残差のヒストグラムに正規分布曲線を追加
xmin, xmax = axs[3].get_xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, residuals_mean, residuals_std)
axs[3].plot(x, p, 'k', linewidth=2)
axs[3].set_xlabel('残差 (Residuals)')
axs[3].set_ylabel('頻度 (Frequency)')
axs[3].set_title('残差のヒストグラム\n(Histogram of Residuals)')
plt.tight_layout()
plt.show()
if __name__ == "__main__":
# データを読み込む
df = pd.read_csv('regression_data.csv')
# 関数の呼び出し(ハイパーパラメータはデフォルト値を使用)
model, y_test, y_pred = train_random_forest_regressor(df, target='特徴量_1', columns=df.columns)
# グラフを描画
plot_figures(y_test, y_pred)回帰結果の評価
精度の評価
| 指標 | 値 |
|---|---|
| 平均絶対誤差 (MAE) | 0.5039958639393453 |
| 平均二乗誤差 (MSE) | 0.3928372697417739 |
| ルート平均二乗誤差 (RMSE) | 0.620.6267673170657305 |
| 平均絶対パーセンテージ誤差 (MAPE) | 2.2027217358416427 |
| 決定係数 (R^2 Score) | 0.6529939477578449 |
MAE、MSE、RMSE、MAPEはそれぞれ誤差の指標です。これを評価する前に、予測対象となる特徴量_1の統計情報を確認しておきましょう。
| 最小値 | 最大値 | 平均値 | 標準偏差 | 分散 |
|---|---|---|---|---|
| -3.4182 | 2.9673 | -0.01889 | 0.9894 | 0.9789 |
平均が0に近く、データの67%が-0.989~+0.989に分布しています。また最小は-3.42、最大は2.98 です。
このデータに対してMAE、MSE、RMSEはそれぞれ 0.5、0.39、0.63 となっており、非常に多くの誤差が含まれていることが分かります。
MAPEは2.2%と小さな値ですが、MAPEの性質上、0付近のデータが多い場合は結果が不正確になるため、今回は過小評価されている可能性が高いです。
また、決定係数の 0.653 はそれほど高い数値ではなく、このモデルを実務で使うのは厳しいと言えます。
次の3つ方法により、精度の改善を目指すべきです。
- ハイパーパラメータの調整: モデルの設定を最適化することで予測精度を向上させる。
- 特徴量の選択とエンジニアリング: 重要な特徴量を追加したり、不要な特徴量を削除する。
- データの前処理: 標準化やスケーリングを行い、モデルの性能を向上させる。
可視化の結果からも、誤差が多く精度が低いことが直感的に読み取れます。

特徴量の重要度
| 特徴量 (Feature) | 重要度 (Importance) |
|---|---|
| 特徴量_2 | 0.705594 |
| 特徴量_6 | 0.066200 |
| 特徴量_7 | 0.061491 |
| 特徴量_5 | 0.056713 |
| 特徴量_3 | 0.056181 |
| 特徴量_4 | 0.053821 |
ランダムフォレストでは、特徴量_1を予測する際に使った特徴量(2~7) において、予測にどの程度寄与したかを数値で表すことができます。
これを見ると、特徴量_2 の重要度が0.705594で、それ以外は0.1未満です。つまり今回のモデルは、ほぼ特徴量_2だけを使って予測していたことが分かります。試しに特徴量_2 だけで予測モデルを作成しても、予測精度はほとんど変わらないでしょう。
このように、重要度を確認することで、予測で使われていない特徴量を把握することができます。
ハイパーパラメータ
予測精度を向上させるには、ハイパーパラメータの調整が重要です。ランダムフォレストには数多くハイパーパラメータが用意されていますが、おおよそ下記の4種類が目安となります。
n_estimators:値を増やすことでモデルの安定性が向上しますが、計算時間も増加します。一般的には100~200の範囲で調整します。
max_depth:過学習を防ぐために適切な深さを見つけることが重要です。デフォルトは無制限ですが、15~30の範囲で試してみるとよいでしょう。
min_samples_split と min_samples_leaf:これらのパラメータを大きくすることで、過学習を防ぐことができます。2~10の範囲で調整します。
max_features:sqrt(n_features) や log2(n_features) などの設定が一般的です。全特徴量の1/3~1/2程度を試してみるとよいでしょう。
| パラメータ名 | 説明 | デフォルト値 |
|---|---|---|
| n_estimators | 決定木の数。ランダムフォレスト内に構築される決定木の数を指定します。 | 100 |
| criterion | 不純度の計算方法。分割基準として使用される関数を指定します分類の場合は、 'gini' または 'entropy' が指定できます。 回帰の場合は、'mse' または 'mae' が指定できます。 | 分類の場合:gini 回帰の場合:mse |
| max_depth | 各決定木の最大深さ。指定がない場合、ノードが2つのサンプルしか持たなくなるまで展開されます。 | None |
| min_samples_split | ノードを分割するために必要なサンプルの最小数。 | 2 |
| min_samples_leaf | リーフノードに必要なサンプルの最小数。 | 1 |
| max_features | 各決定木が分割に使用する特徴量の数。 | auto |
| bootstrap | バギングを使用するかどうか。True の場合、バギングを使用してモデルが作成されます。 | True |
| oob_score | アウト・オブ・バッグサンプルを使用して汎化誤差を推定するかどうかを指定します。 | False |
| n_jobs | 並列に実行するジョブの数。-1 に設定すると、すべてのCPUが使用されます。 | None |
| random_state | 乱数シード。 | None |
| verbose | 詳細な出力のレベル。0 は出力なし、1 は進行状況の出力、2 以上は並列計算の詳細が表示されます。 | 0 |
| warm_start | True に設定すると、前の呼び出しでフィットした解に追加する形でモデルが再利用されます。 | False |
パラメータチューニング手法
ハイパーパラメータのチューニングで最もよく使われるグリッドサーチを使って、ランダムフォレストをチューニングする関数のサンプルです。
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score, mean_absolute_percentage_error
def grid_search_random_forest(df, target, columns, param_grid, test_size=0.2, random_state=42):
"""
グリッドサーチを使用してランダムフォレスト回帰モデルのハイパーパラメータをチューニングし、最適なモデルを見つける関数。
引数:
df : pandas.DataFrame
データを含むデータフレーム。
target : str
予測対象となるターゲット列名。
columns : list of str
使用する特徴量の列名のリスト。ターゲットが含まれていても無視する。
param_grid : dict
グリッドサーチで試すハイパーパラメータの辞書。
test_size : float, optional (default=0.2)
テストデータの割合。
random_state : int, optional (default=42)
乱数シード。
戻り値:
best_model : RandomForestRegressor
最適なハイパーパラメータで訓練されたランダムフォレスト回帰モデルのオブジェクト。
best_params : dict
最適なハイパーパラメータの辞書。
best_score : float
グリッドサーチで得られた最適なスコア。
"""
# 特徴量とターゲットに分ける(target 列を除外)
columns = [col for col in columns if col != target]
X = df[columns]
y = df[target]
# 訓練データとテストデータに分割する
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state)
# ランダムフォレスト回帰モデルのインスタンスを作成する
model = RandomForestRegressor(random_state=random_state)
# グリッドサーチを行う
grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=5, scoring='neg_mean_squared_error', n_jobs=-1)
grid_search.fit(X_train, y_train)
# 最適なモデルとパラメータを取得する
best_model = grid_search.best_estimator_
best_params = grid_search.best_params_
best_score = grid_search.best_score_
# テストデータで予測する
y_pred = best_model.predict(X_test)
# モデルの精度を評価する
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse) # RMSE
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
mape = mean_absolute_percentage_error(y_test, y_pred)
# 精度指標を出力する
print(f'最適なハイパーパラメータ: {best_params}')
print(f'グリッドサーチの最適なスコア: {best_score}')
print(f'平均絶対誤差 (Mean Absolute Error): {mae}')
print(f'平均二乗誤差 (Mean Squared Error): {mse}')
print(f'ルート平均二乗誤差 (Root Mean Squared Error): {rmse}')
print(f'平均絶対パーセンテージ誤差 (MAPE): {mape}')
print(f'決定係数 (R^2 Score): {r2}')
# 特徴量の重要度を表示する
feature_importances = best_model.feature_importances_
importance_df = pd.DataFrame({'特徴量 (Feature)': columns, '重要度 (Importance)': feature_importances})
importance_df = importance_df.sort_values(by='重要度 (Importance)', ascending=False)
print("\n特徴量の重要度:")
print(importance_df)
return best_model, best_params, best_score, y_test, y_pred
if __name__ == "__main__":
# 回帰問題用テストデータの読み込み
df = pd.read_csv('regression_data.csv')
param_grid = {
'n_estimators': [100, 200],
'max_depth': [None, 10, 20],
'min_samples_split': [2, 5],
'min_samples_leaf': [1, 2]
}
best_model, best_params, best_score, y_test, y_pred = grid_search_random_forest(df, target='特徴量_1', columns=df.columns, param_grid=param_grid)
グリッドサーチを行った結果、誤差と精度(決定係数)の改善が果たせました。下記はその結果です。
最適なハイパーパラメータ: {'max_depth': 10, 'min_samples_leaf': 2, 'min_samples_split': 5, 'n_estimators': 100}
グリッドサーチの最適なスコア: -0.3833229336216905
平均絶対誤差 (Mean Absolute Error): 0.4992961662826356
平均二乗誤差 (Mean Squared Error): 0.3895100031970238
ルート平均二乗誤差 (Root Mean Squared Error): 0.6241073651199959
平均絶対パーセンテージ誤差 (MAPE): 2.1650849036473283
決定係数 (R^2 Score): 0.6559330314889025
特徴量の重要度:
特徴量 (Feature) 重要度 (Importance)
0 特徴量_2 0.756729
4 特徴量_6 0.054475
5 特徴量_7 0.051563
3 特徴量_5 0.046980
1 特徴量_3 0.045169
2 特徴量_4 0.045084
ランダムフォレストが簡単に使える自作クラス
ランダムフォレストで分類と回帰のモデルを簡単に作成できるように、必要な機能をまとめたクラスを作りました。
下記に詳しい説明とソースコードを掲載しています。
コピペで使えるようになっていますので、是非ご活用下さい。
【コピペOK】ランダムフォレストやLightGBMを簡単に扱える自作クラスを紹介

まとめ
ランダムフォレストは、分類問題や回帰問題において高い汎化性能を発揮し、多様なデータに柔軟に対応できる強力な機械学習アルゴリズムです。
本記事では、ランダムフォレストの基本的な仕組みやメリット・デメリットを解説し、製造業での活用例や具体的な実装方法についても紹介しました。
また、分類や回帰における評価指標や特徴量の重要度解析、さらに効率的に活用するための便利クラスも提供しました。これらを活用することで、実務においてランダムフォレストを迅速かつ効果的に導入することが可能になります。
ランダムフォレストはシンプルな実装ながら高精度な予測が可能であり、幅広い用途で利用されています。
本記事が、みなさんのプロジェクトや課題解決に少しでも貢献できれば幸いです。









コメント