製造業のデータ分析において、複雑なデータの中から本質的な要因を見極めることは非常に重要です。そこで活躍するのが 因子分析(Factor Analysis, FA)。データに潜む「見えない因子」を明らかにし、プロセス最適化や品質向上につなげる強力な手法です。
この記事では、因子分析の基本的な仕組みから製造業での応用例、Pythonを使った実践的な分析方法までを詳しく解説します。興味のある方は、是非ご一読ください。
因子分析(Factor Analysis, FA)とは何か?
因子分析(Factor Analysis, FA)は、多次元データの背後に潜む共通のパターンや構造を明らかにするための統計的手法です。観測されたデータの中に隠れている「潜在因子(見えない要因)」を抽出することで、データ間の関係性をより深く理解することを目指します。これにより、複雑なデータをシンプルにし、背後にある意味を明確にすることが可能になります。
例えば、製造業では製品の品質やパフォーマンスを測定するために、さまざまな観測変数(例: 温度、圧力、速度)が記録されます。これらの変数には、共通する潜在的な要因(例: 製造工程の特性や機械の性能)が存在することがあります。因子分析を用いることで、観測されたデータの中からこれらの共通因子を抽出し、品質管理や異常検知のための分析に役立てることができます。
因子分析は、「手元にあるデータを要約するための尺度」を数学を用いて計算し、それを「因子」と呼んでいるに過ぎません。
導かれる因子はどれも存在する保証はないため、結果が出ても因子の存在を発見したとは言えません。
逆に、結果が出ない場合、因子が存在しないと断定することもできません。
因子分析(FA)の基本概念
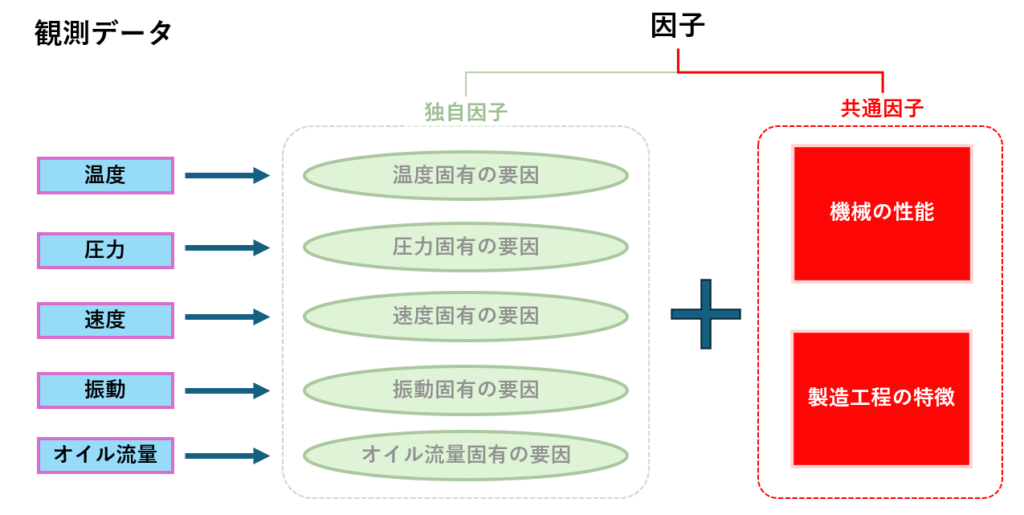
因子分析(FA)は、観測データに潜む「因子(特に共通因子)」と呼ばれる潜在変数を抽出することで機能します。この因子は、複数の観測変数に共通する背後の要因を表しており、データの構造や関連性を明らかにするために使用されます。具体的には、次のような手順で因子を特定します:
- 相関行列の計算
観測変数間の相関を表す相関行列を計算します。これにより、変数間に潜む共通の要因を探索するための基盤を作ります。 - 因子負荷量の推定
相関行列を基に、各観測変数がどの因子にどれだけ関連しているかを表す「因子負荷量」を推定します。 - 因子の回転(必要に応じて)
解釈しやすくするため、因子負荷量を回転(例: バリマックス回転)して因子の意味を明確にします。 - 因子数の決定
因子の数を決定する際には、固有値や累積寄与率などの指標を用います。適切な因子数を選ぶことで、データの簡素化と情報保持のバランスをとります。
因子分析は、観測されたデータが背後にある因子の影響を受けていると仮定する線形手法であり、データ間の相関構造を反映します。
因子分析(FA)の目的
因子分析の目的は、観測変数の背後に潜む共通因子を抽出し、複雑なデータを簡素化しながらその構造を解明することです。具体的には、以下のような点が挙げられます:
- 観測変数を統合して、潜在的な要因を特定する
- データの背後にある構造や関連性を明らかにする
- 潜在因子を利用して、品質管理やプロセス改善などの意思決定に役立てる
因子分析は、データの「潜在的な要因」を見つける点で主成分分析とは異なり、観測変数間の共通性を重視する手法です。
因子分析(FA)の用途
因子分析(FA)は、以下のような幅広い用途に応用されています。
背後にある共通因子の特定
製造現場では、複数のセンサーや機器が記録する変数間には、しばしば共通の要因が存在します。例えば、温度、湿度、圧力などの測定値には、製造工程や機械性能に基づく隠れた要因が影響しています。因子分析を活用することで、これらの共通因子を特定し、以下のような課題を解決できます。
- プロセスの最適化: 主要な要因を特定し、工程の効率化を支援
- 品質向上: データから製品不良の原因となる要因を特定
次元削減
因子分析は、観測変数の情報を要約して少数の因子に集約できるため、次元削減に利用できます。ただし、次元削減のみに特化した用途では、主成分分析(PCA)が選ばれることが一般的です。
- 解釈の容易化: 因子分析では、次元削減の結果として得られる「因子」が具体的な意味を持つ場合が多く、直感的に理解しやすいのが特徴です。
- 計算効率の向上: 必要な要因のみに焦点を当てることで、効率的なモデル構築が可能。
データの圧縮とノイズの除去
因子分析は、データに含まれるノイズや独立した特異点(独自因子)を除去し、質の高いデータセットを構築するのに役立ちます。
- 情報の圧縮: 共通因子を抽出することで、元データを効率的に表現。
- ノイズの除去: 分析に重要でないデータ成分を削減することで、データの品質を向上させます
データの可視化と直感的理解
因子分析を用いることで、観測変数を潜在因子のスコアに変換し、データを可視化することが可能です。これにより、次のような目的が達成されます。
- クラスターの把握: データの分布や類似性を視覚的に確認可能。例として、製品の良品と不良品のグループ化を明確にします。
- 異常点の検出: 潜在因子のスコアから外れたデータ点を識別し、効率的に異常調査が可能になります。
特徴量選択の効率化
因子分析では、観測変数と因子の関連性を示す「因子負荷量」を計算します。この情報を基に、分析に重要な特徴量を選択できます。
- モデルの単純化: 必要な変数のみに絞り込み、シンプルなモデル構築を支援。
- ノイズの削減: 不必要な特徴量を排除することで、データの質を向上。
異常検知
因子分析は主にデータの構造を理解するために使われる手法であり、異常検知そのものを目的とすることは一般的ではありませんが、因子分析の結果を利用して異常検知を行うことは可能です。
- センサー異常の検知: 温度や振動データの異常値検出
- 品質管理: 生産データを分析し、製品の品質異常を早期発見
モデルの前処理
因子分析は、機械学習や統計モデルの前処理としても利用されます。次元削減や特徴量選択を行うことで、効率的な学習を可能にします。
過学習の抑制: 必要な特徴量だけを取り込むことで、モデルの汎化性能が向上。
計算効率の向上: 共通因子のみを使用することで、トレーニング時間を短縮。
因子分析(FA)のメリットとデメリット
因子分析には、FAや他の次元削減手法では得られない特有のメリットがあります。
メリット
- 品質管理の向上:
製品の品質に影響を与える要因を特定し、管理することで全体の品質向上が可能です。 - 工程の最適化:
製造工程における主要な因子を特定することで、工程の最適化や効率化が期待できます。 - コスト削減:
無駄なプロセスや材料の使用を削減し、コスト効率の向上を図ることができます。 - 予測精度の向上:
因子間の関係を理解することで、製品の欠陥や不具合の発生を予測しやすくなります。 - データの簡素化:
多くの変数を少数の因子にまとめることで、データの解釈や分析が容易になります。 - 問題の根本原因の特定:
重大な影響を与える潜在変数を特定し、問題解決の糸口を提供することができます。
デメリット
- 複雑なデータ要求:
因子分析には多くの観測データが必要であり、データ収集が大規模で時間がかかる場合があります。 - 専門知識の必要性:
統計的な手法や結果の解釈には専門的な知識が必要です。 - 仮定の影響:
因子分析は特定の仮定(正規性、線形性など)に基づいており、これらが満たされない場合、結果が信頼できないことがあります。 - 因子の解釈の難しさ:
抽出された因子が具体的に何を意味するのか解釈が難しいことがあります。 - 過度な単純化のリスク:
多くの変数を少数の因子に集約する過程で、重要な情報を失うリスクがあります。 - コストと時間:
実施には高コストと時間がかかる場合があります。
因子分析(FA)が適するデータ、適さないデータ
因子分析(FA)は、特定の条件下で非常に有効な手法ですが、適さない場合もあります。以下に、因子分析が適するデータと適さないデータについて詳しく説明します。
因子分析(FA)が適しているデータ
- 相関が高いデータ:
観測変数間に高い相関が存在するデータに適しています。因子分析は共通因子を抽出するため、変数間の相関が強い場合に有効です。 - 多変量データ:
多くの観測変数があるデータセットに適しています。複数の変数を少数の因子に集約することで、データの解釈が容易になります。 - 連続変数:
通常、連続変数(例えば、スコアや測定値)に適用されます。因子分析はこれらの変数間の共通の構造を抽出します。 - 正規分布しているデータ:
因子分析は、変数が多変量正規分布に従うことを前提としていることが多いです。ただし、実際のデータは必ずしも正規分布に従わない場合もあり、この前提が満たされない場合、分析結果の解釈には注意が必要です。 - 欠損値が少ないデータ:
多くの欠損値が含まれるデータは、因子分析の精度を低下させる可能性があります。欠損値の処理方法によっては、分析結果にバイアスが生じることもあります。 - 大規模なサンプルサイズ:
大規模なサンプルサイズ(通常は100以上)があるデータに適しています。十分なサンプルサイズが必要なため、安定した因子構造を得ることができます。 - 探索的分析:
データの背後にある構造を探索する目的で有効です。データの潜在的なパターンや構造を見つけるために使用されます。
因子分析(FA)が適さないデータ
- 相関が低いデータ:
観測変数間に低い相関があるデータには適しません。相関が低い場合、因子分析は共通因子をうまく抽出できません。 - カテゴリカルデータ:
カテゴリカルデータや名義尺度のデータには適しません。因子分析は連続変数を前提としているため、カテゴリカルデータには不向きです。 - 小規模なサンプルサイズ:
サンプルサイズが小さいデータには適しません。信頼性の高い因子構造を得るためには、十分なサンプルサイズが必要です。 - 線形性がないデータ:
変数間に線形関係がない場合、因子分析は適用できません。因子分析は変数間の線形関係を前提としています。 - 時系列データ: 時系列データは、時間の経過に伴う変化を捉えることが重要であり、因子分析のような静的な手法では、その特徴を十分に捉えられない場合があります。
- 異質な変数の混合: 全く異なる種類の変数をまとめて分析する場合、因子構造が解釈困難になることがあります。例えば、身長、体重などの身体的な特徴と、性格に関する質問項目を同時に分析することは避けるべきです。
因子分析(FA)の基本的な使い方
この章では、自動生成した疑似的なセンサーデータ(下記グラフ波形)を使って、FAの使い方、結果の解釈の仕方を説明します。
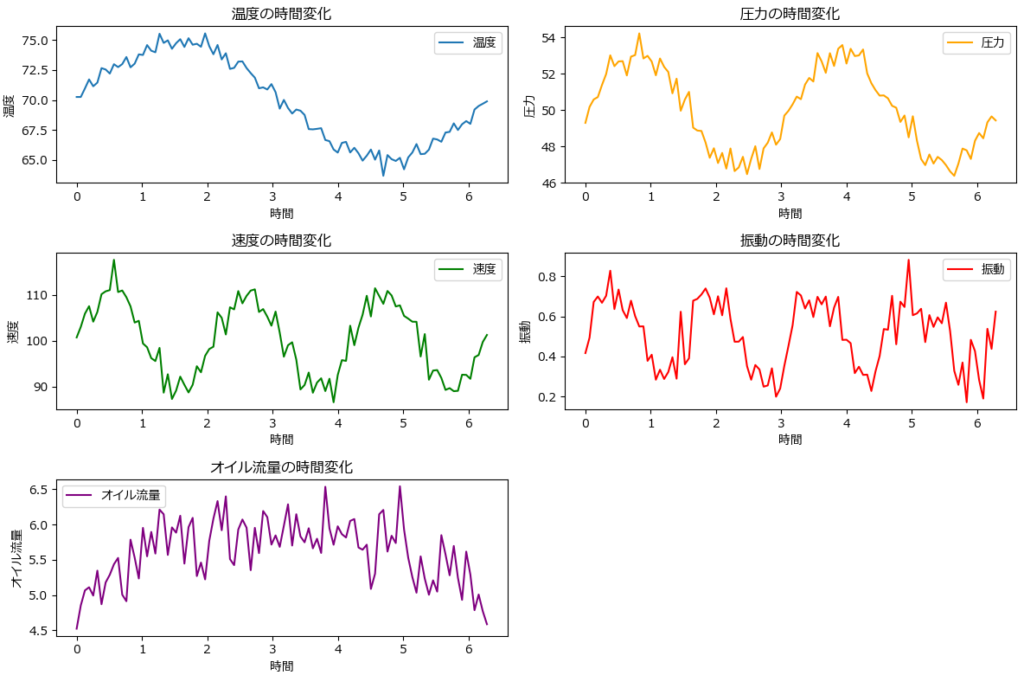
下記はFAのサンプルプログラムです。
各説明変数(特徴量)のスケールが異なると、大きなスケールを持つ変数に結果が引っ張られることになるため、必ず標準化を行います。
pip install factor-analyzer
import numpy as np
import pandas as pd
from factor_analyzer import FactorAnalyzer
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
# ------ダミーデータの生成 --------------------------------------
np.random.seed(42) # シード設定
n_samples = 100 # サンプル数(時間軸を表現するサンプル)
time = np.linspace(0, 2 * np.pi, n_samples) # 時間軸データ(0 ~ 2πの範囲)
temperature = 70 + 5 * np.sin(time) + np.random.normal(0, 0.5, n_samples) # 温度は時間的なシーズン性を模倣(正弦波)
pressure = 50 + 3 * np.sin(2 * time) + np.random.normal(0, 0.5, n_samples) # 圧力の周期性(速度や振動との連動性)
speed = 100 + 10 * np.sin(3 * time) + np.random.normal(0, 2, n_samples) # 速度は工場稼働サイクルを模倣
vibration = 0.5 + 0.2 * np.sin(4 * time) + np.random.normal(0, 0.1, n_samples) # 振動は稼働の影響を反映した正弦波
oil_flow = 5 + 1 * np.sin(time / 2) + np.random.normal(0, 0.3, n_samples) # オイル流量はゆっくりとした変動を模倣
# DataFrameへまとめる
data = pd.DataFrame({
'温度': temperature,
'圧力': pressure,
'速度': speed,
'振動': vibration,
'オイル流量': oil_flow,
})
# ---------------------------------------------
# 標準化
scaler = StandardScaler()
scaled_data = scaler.fit_transform(data)
# 因子分析の適用(2因子を抽出)
fa = FactorAnalyzer(n_factors=2, rotation='varimax')
fa.fit(scaled_data)
# 因子負荷量を取得
loadings = fa.loadings_
print("\n因子負荷量:")
loadings_df = pd.DataFrame(loadings, index=data.columns, columns=[f"Factor{i+1}" for i in range(loadings.shape[1])])
print(loadings_df)
# 共通性(Communalities)の計算
communalities = fa.get_communalities()
print("\n共通性:")
communalities_df = pd.DataFrame(communalities, index=data.columns, columns=['共通性'])
print(communalities_df)
# 固有値(Eigenvalues)と寄与率の計算
eigenvalues, variance_explained, cumulative_explained_variance = fa.get_factor_variance()
print("\n各因子の固有値:")
print(eigenvalues)
print("\n各因子の寄与率:")
print(variance_explained)
print("\n累積寄与率:")
print(cumulative_explained_variance)
# 因子得点の計算
factor_scores = fa.transform(scaled_data)
factor_scores_df = pd.DataFrame(factor_scores, columns=[f"Factor{i+1}" for i in range(fa.n_factors)])
print("\n因子得点(先頭の5点):")
print(factor_scores_df.head())
# Factor1 vs Factor2のプロット
plt.figure(figsize=(10, 6))
plt.scatter(factor_scores[:, 0], factor_scores[:, 1], label="データ")
plt.xlabel("因子1 (Factor1)")
plt.ylabel("因子2 (Factor2)")
plt.title("因子分析: 因子1 vs 因子2")
plt.legend()
plt.grid()
plt.show()
# 累積寄与率と寄与率の棒グラフと折れ線グラフの組み合わせ
plt.figure(figsize=(10, 6))
plt.bar(range(1, len(variance_explained) + 1), variance_explained, alpha=0.5, align='center', label='個別の寄与率')
plt.plot(range(1, len(cumulative_explained_variance) + 1), cumulative_explained_variance, marker='o', label='累積寄与率', linestyle='--')
plt.xlabel("因子数")
plt.ylabel("寄与率")
plt.title("因子分析の寄与率と累積寄与率のグラフ")
plt.legend()
plt.grid()
plt.show()
# 因子負荷量のヒートマップ
plt.figure(figsize=(10, 6))
plt.imshow(loadings, cmap='viridis', aspect='auto')
plt.colorbar(label='負荷量')
plt.xticks(ticks=np.arange(loadings.shape[1]), labels=[f"Factor{i+1}" for i in range(loadings.shape[1])])
plt.yticks(ticks=np.arange(len(data.columns)), labels=data.columns)
plt.xlabel("因子")
plt.ylabel("変数")
plt.title("因子負荷量のヒートマップ")
plt.grid()
plt.show()因子負荷量:
Factor1 Factor2
温度 0.021430 -0.023904
圧力 0.032278 0.302163
速度 -0.118490 0.064307
振動 -0.079814 0.330978
オイル流量 0.982554 0.172389
共通性:
共通性
温度 0.001031
圧力 0.092345
速度 0.018175
振動 0.115917
オイル流量 0.995131
各因子の固有値:
[0.98732378 0.2352743 ]
各因子の寄与率(共通の分散に対する):
[0.19746476 0.04705486]
累積寄与率:
[0.19746476 0.24451961]
因子得点(先頭の5点):
Factor1 Factor2
0 -2.394734 -0.662584
1 -1.703518 -0.273698
2 -1.298644 0.205254
~以下省略~
結果の解釈の仕方
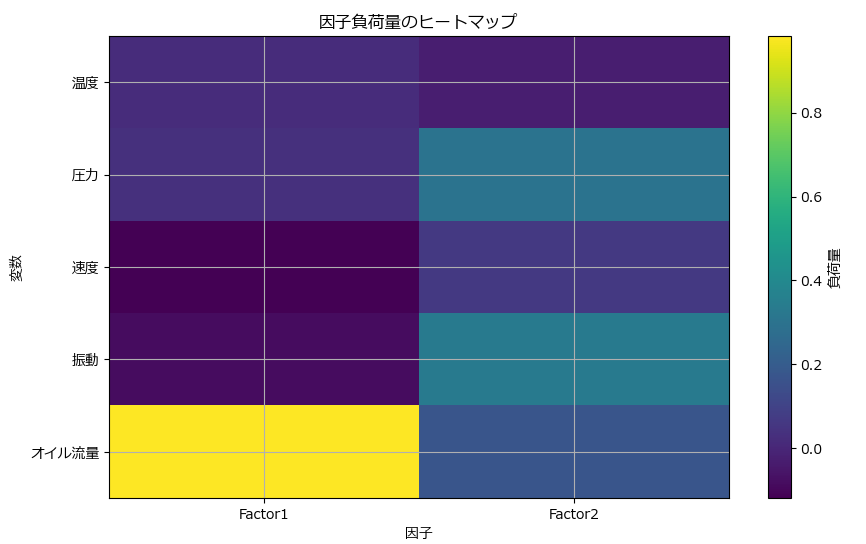
因子負荷量(Factor Loadings)
| 特徴量(変数名) | Factor1 | Factor2 |
|---|---|---|
| 温度 | 0.021430 | -0.023904 |
| 圧力 | 0.032278 | 0.302163 |
| 速度 | -0.118490 | 0.064307 |
| 振動 | -0.079814 | 0.330978 |
| オイル流量 | 0.982554 | 0.172389 |
因子負荷量は、各変数が特定の因子にどの程度関連しているかを示します。
高い負荷量(通常は0.4以上)は、その変数がその因子に強く関連していることを示します。
この例では、Factor1(因子1)主にオイル流量(0.982554)に関連する因子であると解釈できます。その他の変数はほとんど因子1に関与していません。一方、Factor2(因子2)は圧力(0.302163)と振動(0.330978)に高い数値をしてしてることから、因子であると判断できます。
共通性(Communalities)
| 特徴量(変数名) | 共通性 |
|---|---|
| 温度 | 0.001031 |
| 圧力 | 0.092345 |
| 速度 | 0.018175 |
| 振動 | 0.115917 |
| オイル流量 | 0.995131 |
共通性は、全ての因子(この例では因子1と因子2)によって、各変数がどの程度説明されているかを示しています。共通性が高い(0.5以上)場合、その変数は因子モデルによってよく説明されていると解釈されます。
共通性 = (Factor1の負荷量)² + (Factor2の負荷量)² +・・・・・
この例では、オイル流量の共通性が0.995と極めて高いため、因子モデルによってよく説明されていることがわかります。一方、他の特徴量は共通性が低いため、因子モデルであまり説明されていないことがわかります。
以上のことから、オイル流量は因子モデルの主要な要素として機能していますが、その他の変数はあまり説明されていないことから、実使用に適さない可能性が高いです。
共通性を高めるためには、次の対策が考えられます。
- 抽出する因子の数を増す
- データの標準化や変換を再検討など前処理を改善する
- 他の手法を検討する
共通性が低い変数を除外することで因子モデルの適合度が向上することはありますが、その一方で情報の喪失や重要な変数の見落としリスクも考慮する必要があります。最良のアプローチは、共通性が低い変数を除外する前に、因子数の再評価やデータの前処理を見直すことです。
固有値(Eigenvalues)
| Factor1の固有値 | Factor2の固有値 |
|---|---|
| 0.98732378 | 0.2352743 |
固有値は、各因子がデータ全体の分散に対してどれだけの分散を説明しているかを示す指標です。固有値が大きいほど、その因子はより多くの情報(分散)を説明していることを意味し、重要な因子と見なされます。
標準化されたデータを使用する場合、固有値の合計は説明変数の数に等しくなります。例えば、説明変数が3個ある場合、固有値の合計は3になります。
各因子の固有値が1以上であれば、その因子は少なくとも1つの変数分の分散を説明していることになります。
この例では、Factor1、Factor2の共に1未満であることから、要な情報を捉えていない(重要な因子が見つからなかった)と解釈できます。
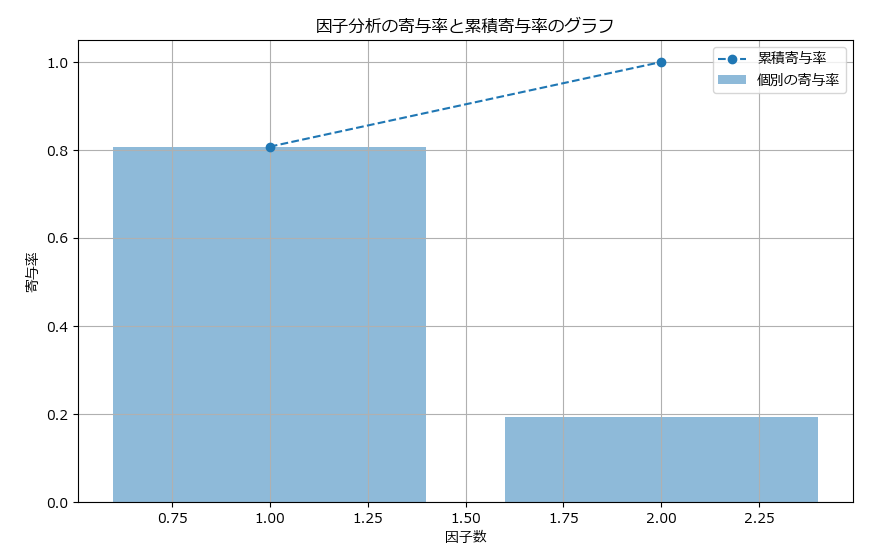
寄与率(Explained Variance Ratio)
| Factor1の寄与率 | Factor2の寄与率 |
|---|---|
| 0.19746476 | 0.04705486 |
寄与率は、各因子の固有値を全固有値の合計で割った割合です。これにより、各因子がデータ全体の分散に対してどれだけの割合を説明しているかが示されます。
寄与率が高いほど、その因子がデータの分散に対して重要な役割を果たしていることを示します。
この例では、Factor1(19.7%)+Factor2(4.7%)= 24.46% であるため、全体の分散を十分に説明できていないと判断できます。固有値と同じアプローチでの改善が必要です。
固有値は、因子ごとの分散の説明量の合計(絶対的な値)であるのに対し、寄与率は、全体の分散を100とした時の比率(個々の因子がどれくらいの割合を占めているかを表す数値)になります。
因子得点(Factor Scores)
| 観測点(データ位置) | Factor1 | Factor2 |
|---|---|---|
| 0 | -2.394734 | -0.662584 |
| 1 | -1.703518 | -0.273698 |
| 2 | -1.298644 | 0.205254 |
| 3 | -1.214047 | 0.297109 |
| ~以下省略~ | ~以下省略~ | ~以下省略~ |
因子得点は、各観測点が因子空間内でどの位置にあるかを示すもので、観測点(個々のデータ)がどの程度各因子に関連しているかを示します。
因子得点は標準化されたデータを基に計算されるため、多くの場合、得点は-3から+3の範囲に収まることが一般的です。ただし、これはあくまで目安であり、極端な得点も存在する場合があります。
通常、因子分析の結果は、全体的なパターンや因子の解釈に重点を置くため、観測点レベルで因子得点を詳細に見ることは、それほど一般的ではありません。
因子分析(FA)を使う上での注意点
- データの標準化が必要:
各特徴量のスケールが異なる場合、大きなスケールを持つ特徴量が因子負荷量に過大な影響を与えることがあります。そのため、因子分析を実行する前にデータを標準化(平均0、分散1)しておくことが重要です。 - 外れ値の処理:
外れ値は因子分析の結果に大きな影響を与えることがあります。適切な方法で外れ値を検出し、処理する必要があります。 - 欠損値の処理:
欠損値がある場合は、削除、代入、または特定の欠損値処理手法を用いて対応する必要があります。 - スケールの影響を意識する:
因子分析は線形性に基づく手法であり、データのスケールや分布が結果に影響を及ぼします。非線形な構造が存在する場合、他の手法(例えば、主成分分析や独立成分分析)も検討してください。 - 次元削減後の情報損失を評価する:
抽出する因子の数によって保持される情報量が変わります。固有値や寄与率を確認し、目的に応じてバランスの取れた選択をしてください。累積寄与率が60%以上であることが望ましいです。 - 過剰解釈のリスクに注意:
因子はデータの構造を表しますが、元の特徴量に比べて直接的な意味が失われることがあります。そのため、結果を過剰に解釈しないよう注意してください。 - 可視化を活用する:
次元削減後のデータを2Dや3Dで可視化することで、データのクラスターや異常値を視覚的に把握しやすくなります。分析結果の理解を深めるために有効です。因子得点のプロットや因子負荷量のヒートマップが役立ちます。 - 目的と結果の整合性を確認:
因子分析の目的が分析の目的に合致しているかを確認してください。次元削減によって失われた情報が重要な場合、他のアプローチや調整を検討する必要があります。
因子分析(FA)の用途別サンプルプログラム
この章で紹介するFAの応用例をご自身のデータに用いる場合は、必ず「因子負荷量」や「共通性」、「固有値」を確認し、結果に十分な情報量が含まれているこを確認しておきましょう。例えば圧縮やノイズ削減を行った際、必要な情報まで削ぎ落されているかもしれません。
下記は、本章で紹介するサンプルプログラムに投入するためのデータを作成するプログラムです。
5次元(5つの説明変数)データを生成しています。
# 共通部分: データ準備
import numpy as np
import pandas as pd
# サンプルデータの生成
np.random.seed(42)
data = pd.DataFrame({
'センサー1': np.random.normal(0, 1, 100),
'センサー2': np.random.normal(1, 2, 100),
'センサー3': np.random.normal(-1, 1, 100),
'センサー4': np.random.normal(0.5, 1.5, 100),
'センサー5': np.random.normal(-0.5, 1, 100),
})実行すると data には下記の通り5次元データが生成されます。
センサー1 センサー2 センサー3 センサー4 センサー5
0 0.496714 -1.830741 -0.642213 -0.743493 -2.094428
1 -0.138264 0.158709 -0.439215 -0.340272 -1.099375
~~~中略~~~
98 0.005113 1.116417 -0.187138 0.328190 -1.375618
99 -0.234587 -1.285941 -0.370371 2.356724 -1.882800
FAを行う場合、データをスケーリングするのが一般的です。
例えば、FAを使って次元削減やノイズ除去をする場合はスケーリングが必要です。
しかし、データの可視化やモデル前処理の準備においては、スケーリングを必ずしも行う必要はありません。
高次元データの次元削減
高次元データは特徴量(変数)が多すぎて、計算や分析が困難になることがあります。因子分析(FA)を使用して、データの最も重要な因子を抽出し、次元を削減します。これにより、データの解釈や可視化が可能になります。
次元削減する場合は n_factors に削減後の次元数(1以上の値)を指定します。下記のサンプルでは2を指定しているため、5次元から2次元に削減されます。
# 必要なライブラリ
from factor_analyzer import FactorAnalyzer
from sklearn.preprocessing import StandardScaler
# スケーリング
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)
# 因子分析の適用(2因子を抽出)
fa = FactorAnalyzer(n_factors=2, rotation='varimax')
fa.fit(data_scaled)
# 因子得点の計算
factor_scores = fa.transform(data_scaled)
print("元のデータの次元:", data.shape)
print("削減後のデータの次元:", factor_scores.shape)
print(factor_scores)元のデータの次元: (100, 5)
削減後のデータの次元: (100, 2)
[[-1.00845841 -0.99294395]
[-0.75097189 -0.30364529]
[ 0.760435 -0.56623137]
~~~以下省略~~~
データの圧縮
高次元データは特徴量(変数)が多すぎて、計算や分析が困難になることがあります。因子分析(FA)を使用して、データの最も重要な因子を抽出し、次元を削減します。これにより、データの解釈や可視化が可能になります。次元削減する場合は n_factors に削減後の次元数を指定します。以下のサンプルでは2を指定しているため、5次元から2次元に削減されます。
データ圧縮では、圧縮後にどれくらい情報を残しておきたいかが重要なので、適切な寄与率を確保することが求められます。例えば、元のデータの情報を80%以上保持したい場合は、選択した因子の累積寄与率が80%以上であることを確認します。
# 必要なライブラリ
from factor_analyzer import FactorAnalyzer
from sklearn.preprocessing import StandardScaler
# データのスケーリング
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)
# 因子分析の適用(寄与率に基づく因子の数の選択)
# ここでは仮に、累積寄与率が0.86に達する因子数を選びます
fa = FactorAnalyzer(rotation='varimax')
fa.fit(data_scaled)
eigenvalues, variance_explained, cumulative_explained_variance = fa.get_factor_variance()
# 累積寄与率が0.86以上になる因子の数を確認
n_factors = np.argmax(cumulative_explained_variance >= 0.86) + 1
# 選ばれた因子数で再度因子分析を実行
fa = FactorAnalyzer(n_factors=n_factors, rotation='varimax')
fa.fit(data_scaled)
# 因子得点の計算
factor_scores = fa.transform(data_scaled)
print("元のデータの次元:", data.shape)
print("圧縮後のデータの次元:", factor_scores.shape)
print(factor_scores)元のデータの次元: (100, 5)
圧縮後のデータの次元: (100, 1)
[[-1.19698268]
[-0.45043731]
[-0.29183094]
~~~以下省略~~~
寄与率の合計を指定した場合、それを保持するために必要な次元数に次元圧縮されるため、データによっては圧縮前と圧縮後の次元数が変わらない(つまり、圧縮できなかった)場合があります。
ノイズの除去
因子負荷量が高いものが重要であることの裏返しとして、寄与率の低い因子はノイズ成分であると考えることができます。寄与率の低いものを除外することでノイズ除去が可能です。
従って、次元削減やデータ圧縮と同じプログラムになりますが、指定する寄与率の合計が異なります。ノイズ除去はデータ品質を高めるため、できるだけ多くノイズを除去したいので、次元数ではなく寄与率の合計を指定し、その値もデータ圧縮より低めの70%~80%を狙うのが一般的です。
# 必要なライブラリ
from factor_analyzer import FactorAnalyzer
from sklearn.preprocessing import StandardScaler
# データのスケーリング
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)
# 因子分析の適用(寄与率に基づく因子の数の選択)
# ここでは仮に、累積寄与率が0.7に達する因子数を選びます
fa = FactorAnalyzer(rotation='varimax')
fa.fit(data_scaled)
eigenvalues, variance_explained, cumulative_explained_variance = fa.get_factor_variance()
# 累積寄与率が0.7以上になる因子の数を確認
n_factors = np.argmax(cumulative_explained_variance >= 0.7) + 1
# 選ばれた因子数で再度因子分析を実行
fa = FactorAnalyzer(n_factors=n_factors, rotation='varimax')
fa.fit(data_scaled)
# 因子得点の計算
factor_scores = fa.transform(data_scaled)
print("元のデータの次元:", data.shape)
print("圧縮後のデータの次元:", factor_scores.shape)
print(factor_scores)元のデータの次元: (100, 5)
圧縮後のデータの次元: (100, 1)
[[-1.19698268]
[-0.45043731]
~~~以下省略~~~
データの可視化
4次元以上のデータは可視化が難しいため、2次元または3次元に変換することで可視化が容易になります。因子分析(FA)を使用して、データの最も重要な因子を抽出し、それを可視化することができます。
以下のサンプルコードでは、因子分析を用いて2次元に次元削減を行い、可視化を行います。
# 必要なライブラリ
from factor_analyzer import FactorAnalyzer
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
# データのスケーリング
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)
# 因子分析の適用(2因子を抽出)
fa = FactorAnalyzer(n_factors=2, rotation='varimax')
fa.fit(data_scaled)
# 因子得点の計算
factor_scores = fa.transform(data_scaled)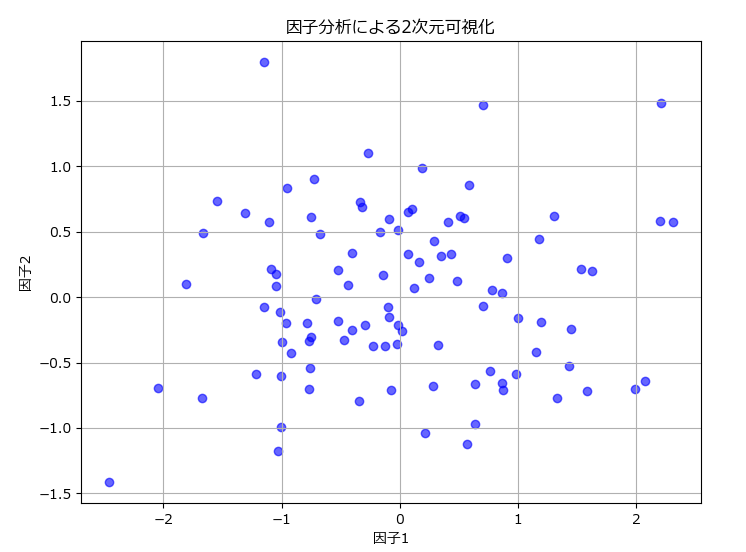
特徴量選択の効率化(スケーリングなし)
因子負荷量は、各特徴量が各因子にどの程度寄与しているかを表しているため、負荷量の大きいものを選ぶことで特徴量選択ができます。この場合も、スケーリングは特に必要ありませんが、データのスケールが異なる場合はスケーリングを行うことで結果の解釈がしやすくなります。
# 必要なライブラリ
from factor_analyzer import FactorAnalyzer
import pandas as pd
# 因子分析の適用(すべての因子を考慮)
fa = FactorAnalyzer(rotation='varimax')
fa.fit(data)
# 特徴量ごとの寄与率(因子負荷量の平均値として計算)
loadings = fa.loadings_
average_loadings = loadings.mean(axis=1)
print("各特徴量の寄与率(因子負荷量の平均):")
print(pd.DataFrame({
'特徴量': data.columns,
'寄与率': average_loadings
}))各特徴量の寄与率(因子負荷量の平均):
特徴量 寄与率
0 センサー1 0.017716
1 センサー2 0.235395
2 センサー3 0.195446
3 センサー4 0.311951
4 センサー5 0.077297
異常検知(スケーリングが必要)
異常検知は再構成誤差を使います。元のデータで作成した因子分析(FA)のモデル(元のデータの主要なパターンや特性を捉えたモデル)に対して新しいデータを投入すると、次元削減されます。これを再構成して元に戻すと、誤差がほとんど発生しないはずです。もし誤差が発生するならば、それはモデル作成時とは異なる分布のデータ=異常データと判断します。
下記サンプルプログラムでは、前述のテストデータで作成したモデルに対して、10個のデータを生成し、異常検知を行っています。
# 必要なライブラリ
from factor_analyzer import FactorAnalyzer
import pandas as pd
import numpy as np
import pickle
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
# ------------------------------------------------
# 正常データを用いたモデルの作成
# ------------------------------------------------
# データのスケーリング
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)
# 因子分析の適用(2因子を抽出)
fa = FactorAnalyzer(n_factors=2, rotation='varimax')
fa.fit(data_scaled)
# 因子負荷量の取得
loadings = fa.loadings_
# モデルの保存
with open('fa_model.pkl', 'wb') as f:
pickle.dump({'model': fa, 'scaler': scaler, 'loadings': loadings}, f)
# ------------------------------------------------
# 新しいデータで異常検知を実施
# ------------------------------------------------
# 新しいデータの生成
new_data = pd.DataFrame({
'センサー1': np.random.rand(10), # 特徴量名を元のデータと一致させる
'センサー2': np.random.rand(10),
'センサー3': np.random.rand(10),
'センサー4': np.random.rand(10),
'センサー5': np.random.rand(10)
})
# データのスケーリング
new_data_scaled = scaler.transform(new_data)
# 因子分析モデルの読み込み
with open('fa_model.pkl', 'rb') as f:
saved = pickle.load(f)
loaded_fa = saved['model']
loaded_scaler = saved['scaler']
loadings = saved['loadings']
# 新しいデータを因子分析モデルで変換
transformed_new_data = loaded_fa.transform(new_data_scaled)
# 再構成誤差の代わりに因子負荷量を用いた再構成
reconstructed_data = np.dot(transformed_new_data, loadings.T)
# スケーリングを元に戻す
reconstructed_data_original_scale = loaded_scaler.inverse_transform(reconstructed_data)
# 再構成誤差の計算(※1)
reconstruction_error = np.mean((new_data.values - reconstructed_data_original_scale)**2, axis=1)
# 再構成誤差の閾値設定(※2)。平均値に標準偏差の3倍(3σ)を加えたもの
threshold = reconstruction_error.mean() + 3 * reconstruction_error.std()
# 誤差(※1)が閾値(※2)を超えているかで異常を判定
is_anomalous = reconstruction_error > threshold
print("新しいデータの再構成誤差:")
print(reconstruction_error)
print("\n異常検知の結果(True = 異常, False = 正常):")
print(is_anomalous)
# 可視化
plt.figure(figsize=(10, 6))
plt.hist(reconstruction_error, bins=30, alpha=0.5, label='新しいデータの再構成誤差')
plt.axvline(threshold, color='r', linestyle='--', label='異常検知の閾値')
plt.xlabel('再構成誤差')
plt.ylabel('頻度')
plt.legend()
plt.title('新しいデータの再構成誤差の分布')
plt.grid()
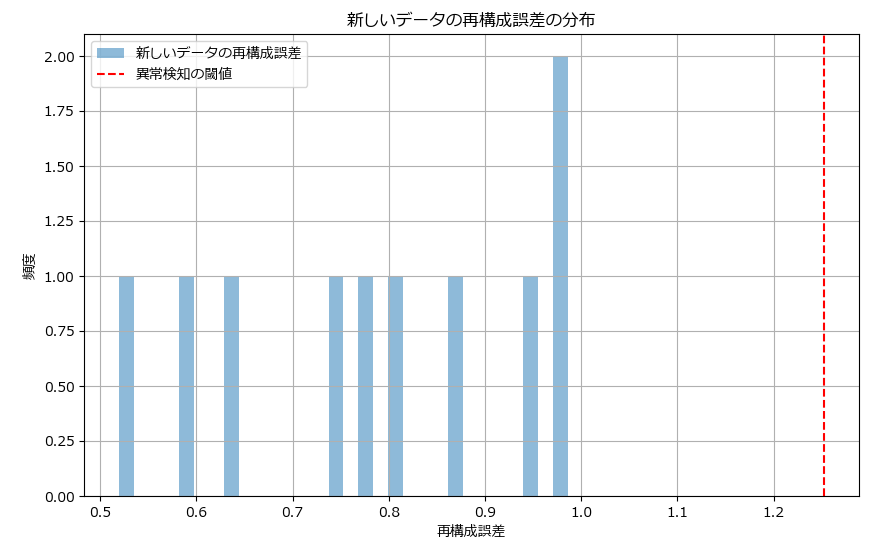
plt.show()今回は10個のデータを投入したので、10個分の判定結果が出力されています。いずれも正常の範囲でした。
新しいデータの再構成誤差:
[0.87233229 0.9860191 0.9816889 0.51990548 0.5959272 0.64055701
0.80085254 0.94567143 0.74772967 0.77077023]
異常検知の結果(True = 異常, False = 正常):
[False False False False False False False False False False]
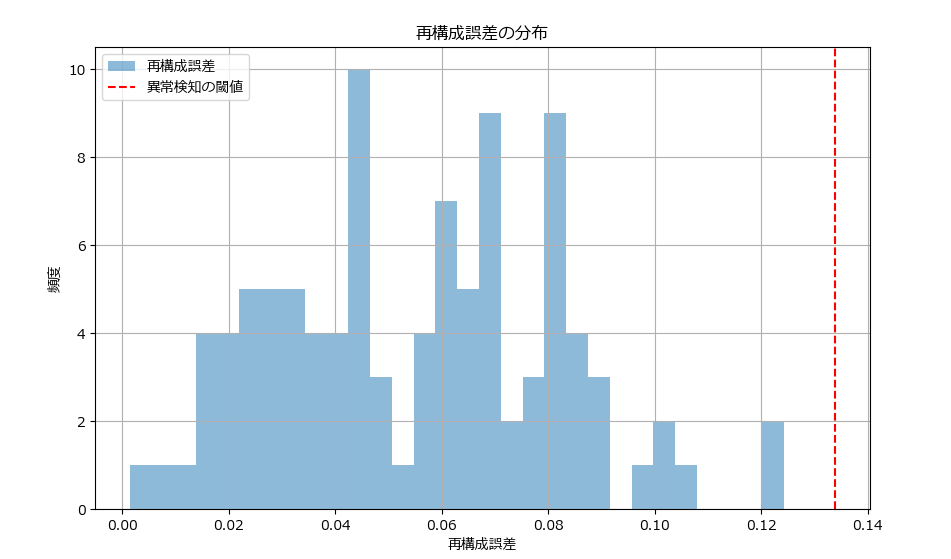
下記は10個のデータにおける再構成誤差のヒストグラムです。赤の点線は異常検知の閾値(平均+3σ)です。異常データがあれば、赤い点線の右にデータ(棒グラフ)に表示されます。
モデルの前処理(スケーリングが必要)
次元削減されたデータをモデルの入力として使用することで、計算効率の向上と過学習の抑制が行えます。以下は、因子分析を用いて次元削減した結果をランダムフォレストの分類モデルで学習させるサンプルプログラムです。
# 必要なライブラリ
from factor_analyzer import FactorAnalyzer
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import numpy as np
import pandas as pd
# ラベルを仮定
np.random.seed(42)
labels = np.random.choice([0, 1], size=100)
# データのスケーリング
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)
# 因子分析による次元削減(2因子を抽出)
fa = FactorAnalyzer(n_factors=2, rotation='varimax')
fa.fit(data_scaled)
data_fa = fa.transform(data_scaled)
#-------------------------------------------------------------------------
# 以下は、次元圧縮した結果を使って、ランダムフォレストのモデルを作成するサンプル
#-------------------------------------------------------------------------
# 学習データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(data_fa, labels, test_size=0.2, random_state=42)
# モデルの学習
model = RandomForestClassifier(random_state=42)
model.fit(X_train, y_train)
# モデルの評価
y_pred = model.predict(X_test)
print("モデルの精度:")
print(accuracy_score(y_test, y_pred))モデルの精度:
0.55
FAが簡単に行える自作クラス
FAとグラフ化が簡単に行える関数とクラスを作ったので紹介します。使い方は次の通りです。
次元削減/データ圧縮/ノイズ除去/特徴量選択など(異常検知以外)
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# ここに後述するグラフ描画関数とFAUtilクラスを張り付けるか、インポートしてください。
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# ステップ1: データの生成
np.random.seed(42)
data = pd.DataFrame({
'feature1': np.random.rand(100),
'feature2': np.random.rand(100),
'feature3': np.random.rand(100),
'feature4': np.random.rand(100),
'feature5': np.random.rand(100)
})
# ステップ2: 因子分析モデルの作成と学習
fa_util = FAUtil(df=data)
fa_util.fit(columns=['feature1', 'feature2', 'feature3', 'feature4', 'feature5'])
# 共通性の取得
communalities = fa_util.model.get_communalities()
print("共通性:")
print(pd.DataFrame(communalities, index=fa_util.columns, columns=['共通性']))
# 固有値と寄与率の取得
eigenvalues, variance_explained, cumulative_explained_variance = fa_util.model.get_factor_variance()
print("固有値:")
print(eigenvalues)
print("寄与率:")
print(variance_explained)
# 因子負荷量の取得
loadings = fa_util.loadings
print("因子負荷量:")
print(loadings)
# グラフの描画
plot_fa_results(fa_util)共通性:
共通性
feature1 0.093713
feature2 0.017329
feature3 0.040791
feature4 1.000240
feature5 0.476106
固有値:
[1.11269512 0.51548395]
寄与率:
[0.22253902 0.10309679]
因子負荷量:
因子1 因子2
feature1 -0.199058 0.232571
feature2 0.018876 -0.130277
feature3 -0.201955 0.002320
feature4 1.000030 0.013421
feature5 0.178518 0.666511
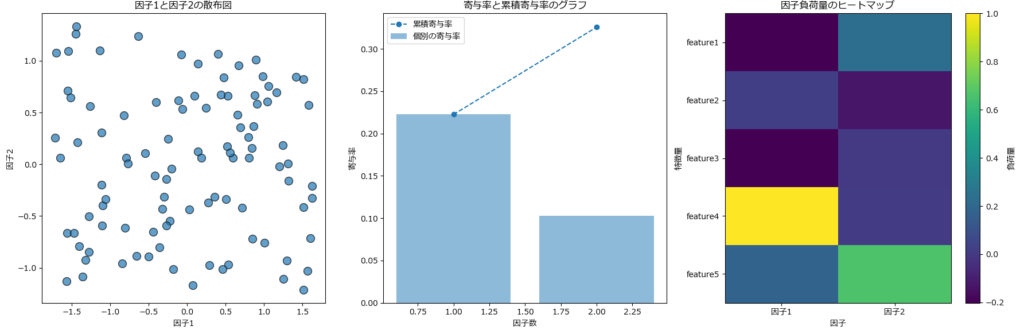
異常検知
異常検知のサンプルプログラムは、5個の説明変数を使ってFAモデルを作成し、10個のテストデータを使って異常検知をしています。FAのモデルはファイルに保存し、異常検知の際には読み込んだモデルを使っています。
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# ここに後述するグラフ描画関数とFAUtilクラスを張り付けるか、インポートしてください。
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# ステップ1: データの生成
np.random.seed(42)
data = pd.DataFrame({
'feature1': np.random.rand(100),
'feature2': np.random.rand(100),
'feature3': np.random.rand(100),
'feature4': np.random.rand(100),
'feature5': np.random.rand(100)
})
# ステップ2: 因子分析モデルの作成と学習
fa_util = FAUtil(df=data)
fa_util.fit(columns=['feature1', 'feature2', 'feature3', 'feature4', 'feature5'])
# モデルの保存
model_path = 'fa_model.pkl'
fa_util.save_model(model_path)
# ステップ3: 新しいデータの生成
new_data = pd.DataFrame({
'feature1': np.random.rand(100),
'feature2': np.random.rand(100),
'feature3': np.random.rand(100),
'feature4': np.random.rand(100),
'feature5': np.random.rand(100)
})
# 新しいデータをFAUtilクラスに設定
fa_util_new = FAUtil(df=new_data)
# 保存したモデルの読み込み
fa_util_new.load_model(model_path)
# ステップ4: 異常検知
anomalies, reconstruction_error, threshold = fa_util_new.detect_anomalies(
columns=['feature1', 'feature2', 'feature3', 'feature4', 'feature5'])
# ステップ5: 結果の表示
print("再構成誤差:")
print(reconstruction_error)
print("\n異常検知の結果(True = 異常, False = 正常):")
print(anomalies)
print("\n異常検知の閾値:")
print(threshold)
# ステップ6: グラフの描画
plot_reconstruction_error_hist(reconstruction_error, threshold)再構成誤差:
[0.05593907 0.08197164 0.03964741 0.08114666 0.08169679 0.08068709
~~中略~~
0.05093812 0.01481158 0.01125312 0.01883125 0.12291929 0.02721396
0.04470847 0.01879897 0.07931506 0.07084543]
異常検知の結果(True = 異常, False = 正常):
[False False False False False False False False False False False False
~~中略~~
False False False False False False False False False False False False
False False False False]
異常検知の閾値:
0.13378009196821516
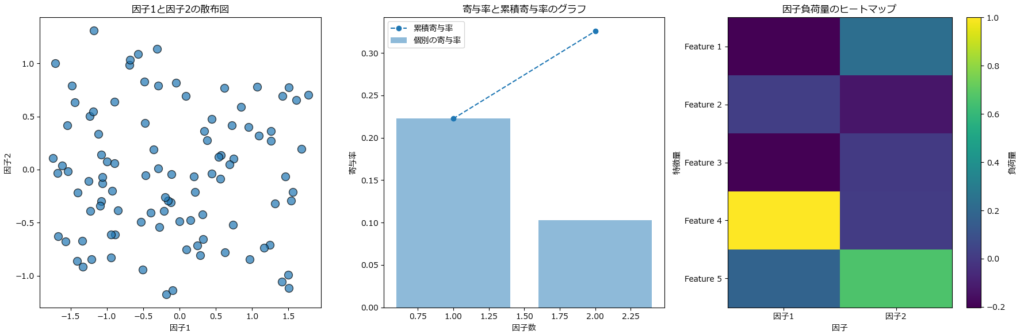
グラフ描画関数のソースコード
| 関数名 | 説明 | パラメーター | 戻り値 |
|---|---|---|---|
| plot_fa_results | FAの結果をプロットする関数。 | fa: 学習済みのFAモデル | なし |
| plot_reconstruction_error_hist | 再構成誤差のヒストグラムをプロットする関数。 | reconstruction_error : 再構成誤差の配列threshold : 異常検知の閾値。 | なし |
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import rcParams
from factor_analyzer import FactorAnalyzer
rcParams['font.family'] = 'Meiryo'
# 因子分析の結果をプロットする関数
def plot_fa_results(fa_util):
"""
因子分析の結果をプロットする関数。
Parameters:
fa_util : FAUtil
学習済みのFAUtilモデル。
"""
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
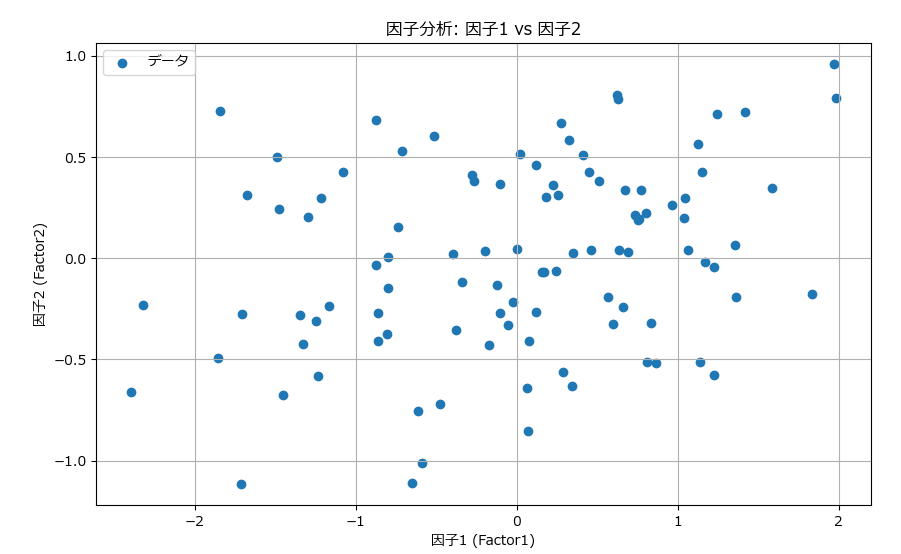
# 因子1 vs 因子2の散布図
scatter = axes[0].scatter(fa_util.transformed_data[:, 0], fa_util.transformed_data[:, 1], alpha=0.7, edgecolors='k', s=100)
axes[0].set_xlabel('因子1')
axes[0].set_ylabel('因子2')
axes[0].set_title('因子1と因子2の散布図')
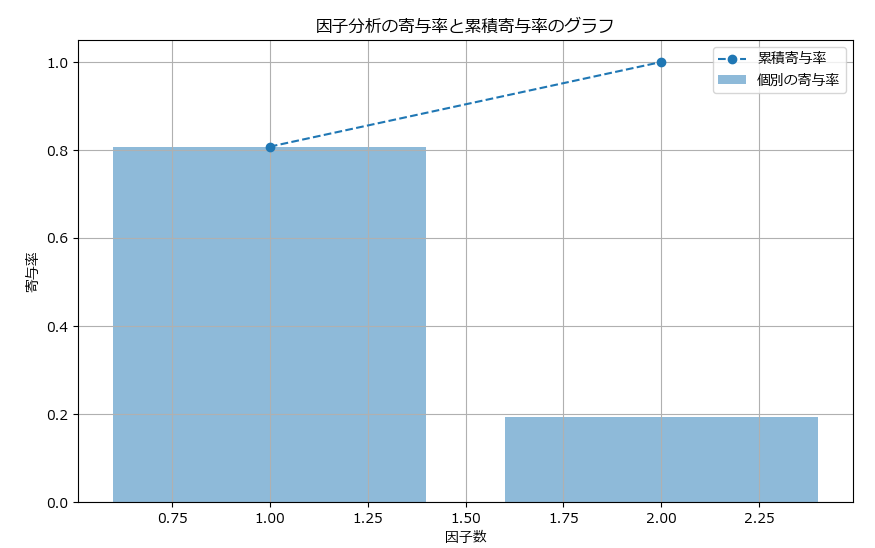
# 寄与率と累積寄与率の棒グラフと折れ線グラフの組み合わせ
eigenvalues, variance_explained, cumulative_explained_variance = fa_util.model.get_factor_variance()
axes[1].bar(range(1, len(variance_explained) + 1), variance_explained, alpha=0.5, align='center', label='個別の寄与率')
axes[1].plot(range(1, len(cumulative_explained_variance) + 1), cumulative_explained_variance, marker='o', label='累積寄与率', linestyle='--')
axes[1].set_xlabel("因子数")
axes[1].set_ylabel("寄与率")
axes[1].set_title("寄与率と累積寄与率のグラフ")
axes[1].legend()
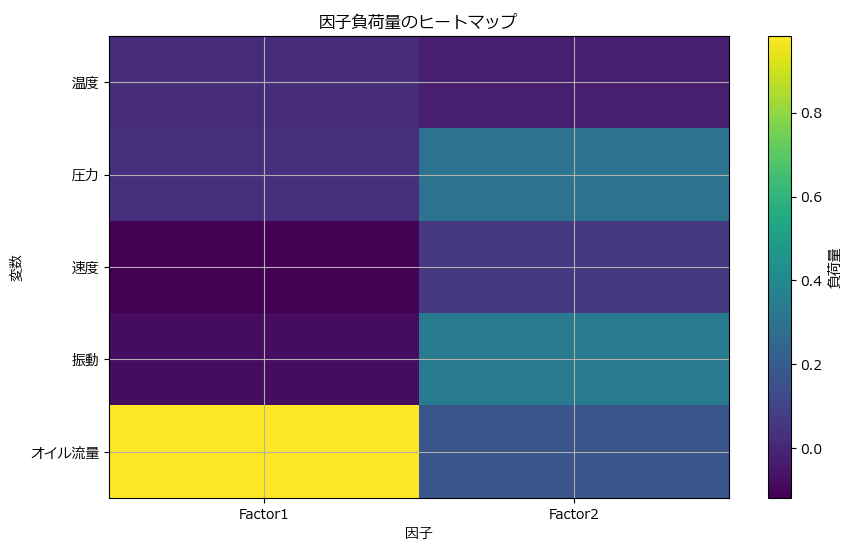
# 因子負荷量のヒートマップ
cax = axes[2].imshow(fa_util.loadings, cmap='viridis', aspect='auto')
plt.colorbar(cax, ax=axes[2], orientation='vertical', label='負荷量')
axes[2].set_xticks(np.arange(fa_util.n_factors))
axes[2].set_xticklabels([f"因子{i+1}" for i in range(fa_util.n_factors)])
axes[2].set_yticks(np.arange(len(fa_util.columns)))
axes[2].set_yticklabels([f"Feature {i+1}" for i in range(fa_util.df.shape[1])])
axes[2].set_xlabel("因子")
axes[2].set_ylabel("特徴量")
axes[2].set_title("因子負荷量のヒートマップ")
plt.tight_layout()
plt.show()
# 再構成誤差のヒストグラムをプロットする関数
def plot_reconstruction_error_hist(reconstruction_error, threshold):
"""
再構成誤差のヒストグラムをプロットする関数。
Parameters:
reconstruction_error : array-like
再構成誤差の配列。
threshold : float
異常検知の閾値。
"""
plt.figure(figsize=(10, 6))
plt.hist(reconstruction_error, bins=30, alpha=0.5, label='再構成誤差')
plt.axvline(threshold, color='r', linestyle='--', label='異常検知の閾値')
plt.xlabel('再構成誤差')
plt.ylabel('頻度')
plt.legend()
plt.title('再構成誤差の分布')
plt.grid()
plt.show()FA便利クラスのソースコード
| メソッド名 | 説明 | パラメーター | 戻り値 |
|---|---|---|---|
| __init__ | FAUtilクラスの初期化メソッド。 | df : 分析に使用するデータフレーム (オプション)。 model_path : 保存済みFAモデルのパス (オプション)。 | なし |
| fit | FAモデルの作成と学習を行うメソッド。 | columns : FAを適用するデータフレームのカ ラム名のリスト。 n_components : FAで抽出する主成分の数 (デフォルトは2) scale : スケーリングの指定 (デフォルトはTrue) | PFA |
| transform | 学習済みモデルを使用してデータを変換するメソッド。 | columns : 変換するデータフレームのカラム名のリスト(省略するとモデル作成時に指定したカラム名のリストが使用される) scale : スケーリングの指定 (デフォルトはTrue) | numpy.ndarray |
| read_csv | CSVファイルを読み込むメソッド。 | file_name : 読み込むCSVファイルのパス。encoding : ファイルのエンコーディング (デフォルトは"shift-jis")。 | なし |
| save_model | FAモデルをファイルに保存するメソッド。 | model_path : 保存するファイルのパス。 | なし |
| load_model | 保存済みFAモデルを読み込むメソッド。 | model_path : 読み込むFAモデルのファイルのパス(デフォルトはNone)。 | FA |
| detect_anomalies | データの異常検知を行うメソッド。 | columns : 異常検知を行うデータフレームのカラム名のリスト (省略すると、fitまたはtransformで指定したカラム名のリストが使用される)。threshold : 異常とみなす再構成誤差の閾値(デフォルトはNoneで、再構成誤差の平均 + 3 * 標準偏差が設定される) scale : スケーリングの指定 (デフォルトはTrue) | tuple : 異常フラグの配列、再構成誤差の配列、閾値。 |
import numpy as np
import pandas as pd
from factor_analyzer import FactorAnalyzer
from sklearn.preprocessing import StandardScaler
import pickle
# FAUtilクラス
class FAUtil:
def __init__(self, df=None, model_path=None):
"""
FAUtilクラスの初期化メソッド。
Parameters:
df : pandas.DataFrame, optional
分析に使用するデータフレーム。デフォルトはNone。
model_path : str, optional
保存済み因子分析モデルのパス。デフォルトはNone。
"""
self.df = None if df is None else df.copy()
self.model = None if model_path is None else self.load_model(model_path)
self.transformed_data = None # 因子分析で変換されたデータ
self.explained_variance_ratio = None # 寄与率
self.loadings = None # 因子負荷量
self.n_factors = None # 因子の数
self.columns = []
self.scaler = StandardScaler()
def fit(self, columns, n_factors=2, scale=True):
"""
因子分析モデルの作成と学習を行うメソッド。
Parameters:
columns : list of str
因子分析を適用するデータフレームのカラム名のリスト。
n_factors : int, optional
因子分析で抽出する因子の数。デフォルトは2。
scale : bool, optional
データをスケーリングするかどうか。デフォルトはTrue。
Returns:
FactorAnalyzer
学習済みの因子分析モデル。
"""
self.columns = columns
X = self.df[columns].values
if scale:
X = self.scaler.fit_transform(X)
self.model = FactorAnalyzer(n_factors=n_factors, rotation='varimax').fit(X)
self.transform(columns, scale=scale)
return self.model
def transform(self, columns=None, scale=True):
"""
学習済みモデルを使用してデータを変換するメソッド。
Parameters:
columns : list of str
変換するデータフレームのカラム名のリスト。
省略するとモデル作成時に指定したカラム名のリストが使用される。
scale : bool, optional
データをスケーリングするかどうか。デフォルトはTrue。
Returns:
numpy.ndarray
変換されたデータ。
"""
if columns is None:
columns = self.columns
else:
self.columns = columns
X = self.df[columns].values
if scale:
X = self.scaler.fit_transform(X)
self.transformed_data = self.model.transform(X)
eigenvalues, variance_explained, cumulative_explained_variance = self.model.get_factor_variance()
self.explained_variance_ratio = variance_explained
self.n_factors = self.model.n_factors
self.loadings = pd.DataFrame(self.model.loadings_,
index=self.columns, columns=[f"因子{i+1}" for i in range(self.n_factors)])
return self.transformed_data
def read_csv(self, file_name, encoding="shift-jis"):
"""
CSVファイルを読み込むメソッド。
Parameters:
file_name : str
読み込むCSVファイルのパス。
encoding : str, optional
ファイルのエンコーディング。デフォルトは"shift-jis"。
"""
self.df = pd.read_csv(file_name, encoding=encoding)
def save_model(self, model_path):
"""
因子分析モデルをファイルに保存するメソッド。
Parameters:
model_path : str
保存するファイルのパス。
"""
self.model_path = model_path
with open(model_path, 'wb') as f:
pickle.dump({
'model': self.model,
'scaler': self.scaler,
'loadings': self.loadings
}, f)
def load_model(self, model_path=None):
"""
保存済み因子分析モデルを読み込むメソッド。
Parameters:
model_path : str, optional
読み込む因子分析モデルのファイルのパス。デフォルトはNone。
Returns:
FactorAnalyzer
読み込まれた因子分析モデル。
"""
model_path = model_path if model_path else self.model_path
with open(model_path, 'rb') as f:
saved = pickle.load(f)
self.model = saved['model']
self.scaler = saved['scaler']
self.loadings = saved['loadings']
return self.model
def detect_anomalies(self, columns=None, threshold=None, scale=True):
"""
データの異常検知を行うメソッド。
Parameters:
columns : list of str
異常検知を行うデータフレームのカラム名のリスト。
省略すると、fit 又は transform で指定したカラム名のリストが使用される。
threshold : float, optional
異常とみなす再構成誤差の閾値。デフォルトはNoneで、
再構成誤差の平均 + 3 * 標準偏差が設定されます。
scale : bool, optional
データをスケーリングするかどうか。デフォルトはTrue。
Returns:
tuple
異常フラグの配列、再構成誤差の配列、閾値。
"""
# データを変換
columns = self.columns if columns is None else columns
self.transform(columns, scale=scale)
# 因子負荷量を用いた再構成
reconstructed_data = np.dot(self.transformed_data, self.loadings.T)
if scale:
reconstructed_data = self.scaler.inverse_transform(reconstructed_data)
# 再構成誤差を計算
reconstruction_error = np.mean((self.df[columns].values - reconstructed_data)**2, axis=1)
# 閾値を設定(デフォルトは再構成誤差の平均 + 3 * 標準偏差)
if threshold is None:
threshold = reconstruction_error.mean() + 3 * reconstruction_error.std()
# 異常検知
anomalies = reconstruction_error > threshold
return anomalies, reconstruction_error, threshold
まとめ
本記事では、因子分析関の基本的な概念から応用例まで幅広く紹介しました。因子分析(FA)は、データの背後にある潜在構造を明らかにし、次元削減やデータ圧縮、ノイズ除去などに役立つ強力なツールです。
FAを活用することで、複雑なデータセットの理解が深まり、予測モデルの精度向上やデータの可視化、異常検知など、多岐にわたる領域で効果を発揮します。また、データ分析の前処理や特徴量選択の一環としても非常に有用です。
本記事を通じて、因子分析の基本とその応用方法についての理解が深まることを願っています。もし実際にFAを用いてデータ分析を行う際には、この記事を参考にして頂ければ幸いです。









コメント