「データ分析の舞台裏で、重要な役割を果たす影の立役者」、それが主成分分析(PCA)です。
『膨大なデータをどう整理すればいい?』『関係性をどう見抜く?』そんな課題に答えてくれます。
PCAは、データの次元削減や要因分析でよく使われますが、それ以外にも様々な使い方があります。
本記事では、PCAの実践的な使い方を中心に、Pythonのサンプルコードとともにわかりやすく解説します。もしかすると今まで知らなかった便利な使い方が見つかるかも。興味のある方は、是非ご一読ください。
主成分分析(PCA)とは何か?
主成分分析(Principal Component Analysis, PCA)は、多次元データの中に隠れているパターンや特徴を抽出するための統計的手法です。データの次元を削減しつつ、元の情報をできるだけ保持することを目指します。これにより、複雑なデータをシンプルにし、解釈しやすくすることが可能になります。
例えば、製造業ではセンサーや機械から大量のデータが収集されます。これらのデータは多次元にまたがることが多く、全てをそのまま扱うのは難しい場合があります。そこでPCAを用いると、データの次元を減らしながら重要な特徴を維持し、効率的な分析や可視化が可能になります。
主成分分析(PCA)の基本概念
PCAは、データの中にある「主成分」と呼ばれる軸を見つけることで機能します。この主成分は、データの分散が最大となる方向を表しています。具体的には、次のような手順で主成分を特定します:
- 共分散行列の計算
データの分散と相関を表す共分散行列を計算します。 - 固有値と固有ベクトルの計算
共分散行列から固有値と固有ベクトルを求めます。これにより、データの主要な軸が明らかになります。 - 主成分の選択
固有値が大きい順に主成分を選びます。これにより、元の次元を減らしつつ、情報の大部分を保持することが可能です。
PCAは基本的に線形手法であり、元データの線形的な構造を反映するものです。
主成分分析(PCA)の目的
主成分分析(PCA)の目的は、複数の説明変数を統合し、データの情報をなるべく損なわない新しい指標(主成分)を得ることです。この新しい指標は、元のデータの相関構造を反映しており、高次元データを効率よく表現してくれます。
主成分分析(PCA)の用途
主成分分析(PCA)によってもたらされる効果は、複数の説明変数が統合(=次元削減)されるということです。これを利用することで、以下に述べる用途が実現できます。
高次元データの次元削減
製造現場では、多数のセンサーや計測器から膨大なデータが収集されます。しかし、高次元データは次のような課題を抱えています。
- 計算負荷の増加: 次元が増えるほど、データの処理やモデル構築にかかる計算時間が増加します。
- 解釈の難しさ: 高次元データの傾向や特徴を把握することは直感的には困難です。
PCAは、これらの課題を解決します。重要な主成分のみを残すことで、データの次元を減らし、効率的な分析を可能にします。次元削減により、以下の利点が得られます。
- モデルの計算効率向上
- 可視化によるデータの直感的理解
- 過学習のリスク軽減
データの圧縮
次元削減を通じて、データの情報量を損なわずに効率的な保存や通信が可能になります。PCAは主成分を選択することで、元のデータの分散をほぼ保持します。これにより少ない次元でも同等の分析結果を得られます。
- 大規模データを軽量化し、ストレージや通信コストを削減
- 元データの近似表現を作成しつつ、高い分析精度を保持
ノイズの除去
製造現場で得られるデータには、しばしばノイズ(分析において重要でない成分)が含まれます。
PCAはデータの分散を基にして重要な成分を抽出するため、ノイズを効果的に削減できます。これにより、次のような結果が期待されます。
- データの品質向上
- モデルの精度向上
データの可視化と直感的理解
PCAを用いることで、高次元データを2次元や3次元に射影できます。これにより、次のような目的が達成されます。
- クラスターの把握: データの分布や類似性を視覚的に確認可能。例として、製品の良品と不良品の分布を確認できます。
- 異常点の検出: 異常データが視覚的に目立つ形で表示され、原因調査の効率が向上します。
特徴量選択の効率化
製造業のデータには、多数の特徴量(変数)が含まれますが、それらすべてが有用とは限りません。PCAを活用することで、重要な特徴量を抽出し、モデル構築において以下の利点を得られます。
- モデルのシンプル化
- 不必要な特徴量によるノイズや過学習の防止
異常検知
製造ラインや設備のモニタリングにおいて、異常検知は重要な課題です。PCAを用いることで、通常のデータから逸脱する異常点を発見できます。具体的な例として以下が挙げられます。
- センサー異常の検知: 温度や振動データの異常値検出
- 品質管理: 生産データを分析し、製品の品質異常を早期発見
モデルの前処理
PCAは機械学習や統計モデルの入力データを効率化するための前処理として利用されます。
次元削減により、以下の効果が期待できます。
- 計算効率の向上: 次元削減により、学習モデルのトレーニング時間を短縮。
- 過学習の抑制: 不必要な特徴量を排除することで、モデルの汎化性能が向上。
例: 製造データをPCAで前処理し、不良品検出モデルの学習時間を短縮するとともに、精度向上を実現。
主成分分析(PCA)のメリットとデメリット
PCAは強力なデータ分析ツールですが、どんな手法にも利点と課題があります。以下では、PCAのメリットとデメリットを整理します。
メリット
- 次元削減による効率化
高次元データを低次元に圧縮することで、データの処理速度や計算効率が向上します。
例: 高次元の画像データやセンサーデータを簡略化して分析する。 - ノイズの削減
データに含まれる不必要な成分(ノイズ)を取り除き、重要な情報を強調します。
例: センサー計測での微小な揺らぎや誤差を軽減。 - 相関関係の解消
相関が強い変数をまとめて新しい主成分として表現することで、冗長性を取り除きます。
例: 類似した変数が多いマーケティングデータの整理。 - 可視化の容易さ
次元削減により2次元や3次元の空間にデータをプロットできるため、クラスターやトレンドを視覚的に確認できます。
例: 顧客セグメンテーションの可視化。 - 機械学習モデルの改善
次元削減によってモデルの学習速度が向上し、過学習のリスクを軽減します。
例: ランダムフォレストやサポートベクターマシンなどのアルゴリズムでの適用。
デメリット
- 結果の解釈が難しい
主成分は元の特徴量の線形結合として定義されるため、具体的な意味を持たない場合があります。
例: 「主成分1」が何を表しているかを直感的に理解するのが難しい。 - 非線形データへの非対応
PCAは線形手法のため、非線形な関係性を持つデータには適しません。
代替案: カーネルPCAやt-SNE、UMAPなどの非線形次元削減手法。 - 情報の一部損失
次元削減の過程で、主要な成分以外の情報が削除されるため、重要な情報を失う可能性があります。
対策: 寄与率や固有値を確認し、適切な主成分数を選ぶ。 - 前処理が必須
スケールが異なる特徴量がある場合は標準化が必要で、手間が増える。
例: cm単位の特徴量とkg単位の特徴量が混在している場合。 - 欠損値への弱さ
欠損値を含むデータではPCAが正確に動作しないため、事前の補完が必要です。
対策: 平均値補完や近傍補完などの方法を適用。 - すべての課題を解決するわけではない
PCAは次元削減が主目的であり、クラスター形成や分類、異常検知を直接行う手法ではありません。
補足: PCAを前処理として利用し、その後の分析手法と組み合わせることが一般的。
主成分分析(PCA)が適するデータ、適さないデータ
PCAは強力な次元削減ツールですが、すべてのデータセットで最適な手法というわけではありません。ここでは、PCAが得意とするデータや適さないケースについて解説し、実務で注意すべきポイントを紹介します。
主成分分析(PCA)が適しているデータ
- 高次元データ
PCAは多次元データを少数の重要な成分に圧縮するのが得意です。次元が多いほどデータの解釈が難しくなるため、情報を要約するPCAの利点が活きます。
例: センサーや製造装置からの多変量データ。 - 相関の強い変数が多いデータ
相関が強い変数は、同じ情報を重複して持っている可能性があります。PCAは相関を考慮し、冗長性を取り除いて主要な軸を抽出します。
例: 温度や湿度、圧力などが密接に関連するデータ。 - 分散がデータの重要性を反映しているデータ
PCAは分散が大きい方向を主成分として選びます。そのため、分散の大小がデータの特徴量の重要性を示す場合に効果を発揮します。
例: 顧客行動や製品品質の変動データ。
主成分分析(PCA)が適さないデータ
- 非線形な関係が重要なデータ
PCAは線形手法のため、データ内の非線形なパターンを捉えることはできません。
代替案: カーネルPCAやt-SNEなどの非線形次元削減手法。 - カテゴリカルデータが主体のデータ
PCAは数値データを前提としているため、カテゴリカルデータには直接適用できません。
代替案: One-Hot Encodingで数値化するか、別の解析手法を検討。 - 分散が分析目標と一致しないデータ
分散が大きいほど重要とは限らない場合、PCAの結果が適切でないことがあります。
例: 異常検知で小さな変化を検出したい場合。 - 欠損値が多いデータ
PCAはデータが完全であることを前提とします。欠損値が多い場合は前処理が必要です。
対策: 欠損値補完や削除を行ったうえでPCAを適用。
主成分分析(PCA)の基本的な使い方
この章では、自動生成した疑似的なセンサーデータ(下記グラフ波形)を使って、PCAの使い方、結果の解釈の仕方を説明します。
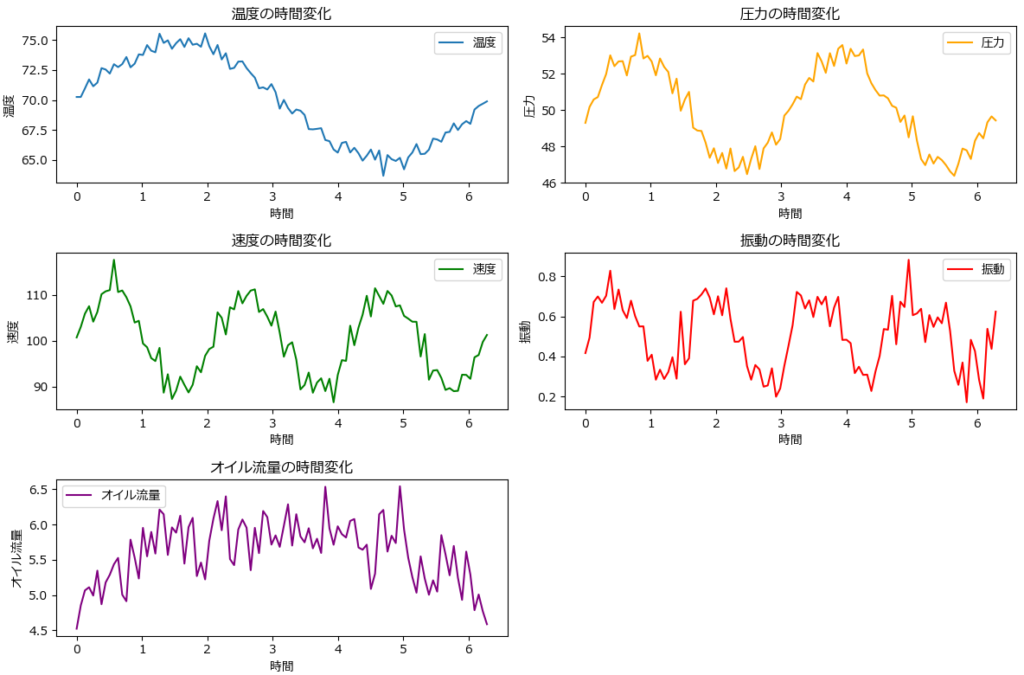
下記はPCAのサンプルプログラムです。
各説明変数(特徴量)のスケールが異なると、大きなスケールを持つ変数に結果が引っ張られることになるため、必ず標準化を行います。
import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
# ------ダミーデータの生成 --------------------------------------
np.random.seed(42) # シード設定
n_samples = 100 # サンプル数(時間軸を表現するサンプル)
time = np.linspace(0, 2 * np.pi, n_samples) # 時間軸データ(0 ~ 2πの範囲)
temperature = 70 + 5 * np.sin(time) + np.random.normal(0, 0.5, n_samples) # 温度は時間的なシーズン性を模倣(正弦波)
pressure = 50 + 3 * np.sin(2 * time) + np.random.normal(0, 0.5, n_samples) # 圧力の周期性(速度や振動との連動性)
speed = 100 + 10 * np.sin(3 * time) + np.random.normal(0, 2, n_samples) # 速度は工場稼働サイクルを模倣
vibration = 0.5 + 0.2 * np.sin(4 * time) + np.random.normal(0, 0.1, n_samples) # 振動は稼働の影響を反映した正弦波
oil_flow = 5 + 1 * np.sin(time / 2) + np.random.normal(0, 0.3, n_samples) # オイル流量はゆっくりとした変動を模倣
# DataFrameへまとめる
data = pd.DataFrame({
'温度': temperature,
'圧力': pressure,
'速度': speed,
'振動': vibration,
'オイル流量': oil_flow,
})
# ---------------------------------------------
# 標準化
scaler = StandardScaler()
scaled_data = scaler.fit_transform(data)
# PCAの適用(必要な成分数を指定しない)
pca = PCA()
pca_data = pca.fit_transform(scaled_data)
# 累積寄与率を計算
cumulative_explained_variance = np.cumsum(pca.explained_variance_ratio_)
# 結果表示
print("各主成分の寄与率:")
print(pca.explained_variance_ratio_)
print("\n累積寄与率:")
print(cumulative_explained_variance)
print("\n主成分の負荷量:")
loadings = pd.DataFrame(pca.components_.T, index=data.columns, columns=[f"PC{i+1}" for i in range(pca.n_components_)])
print(loadings)
# PC1 vs PC2のプロット
plt.figure(figsize=(10, 6))
plt.scatter(pca_data[:, 0], pca_data[:, 1], label="データ")
plt.xlabel("主成分1 (PC1)")
plt.ylabel("主成分2 (PC2)")
plt.title("PCA: 主成分1 vs 主成分2")
plt.legend()
plt.grid()
plt.show()
# 累積寄与率と寄与率の棒グラフと折れ線グラフの組み合わせ
plt.figure(figsize=(10, 6))
plt.bar(range(1, len(pca.explained_variance_ratio_) + 1), pca.explained_variance_ratio_, alpha=0.5, align='center', label='個別の寄与率')
plt.plot(range(1, len(cumulative_explained_variance) + 1), cumulative_explained_variance, marker='o', label='累積寄与率', linestyle='--')
plt.xlabel("主成分数")
plt.ylabel("寄与率")
plt.title("寄与率と累積寄与率のグラフ")
plt.legend()
plt.grid()
plt.show()
# 主成分負荷量のヒートマップ
plt.figure(figsize=(10, 6))
plt.imshow(loadings, cmap='viridis', aspect='auto')
plt.colorbar(label='負荷量')
plt.xticks(ticks=np.arange(pca.n_components_), labels=[f"PC{i+1}" for i in range(pca.n_components_)])
plt.yticks(ticks=np.arange(len(data.columns)), labels=data.columns)
plt.xlabel("主成分")
plt.ylabel("変数")
plt.title("主成分負荷量のヒートマップ")
plt.grid()
plt.show()各主成分の寄与率:
[0.22574995 0.2212905 0.20220346]
主成分の負荷量:
PC1 PC2 PC3
温度 -0.053397 -0.057248 0.945361
圧力 0.516691 0.519379 0.069801
速度 -0.474457 0.483609 0.234929
振動 0.159732 0.668543 -0.078961
オイル流量 0.692500 -0.214804 0.199985
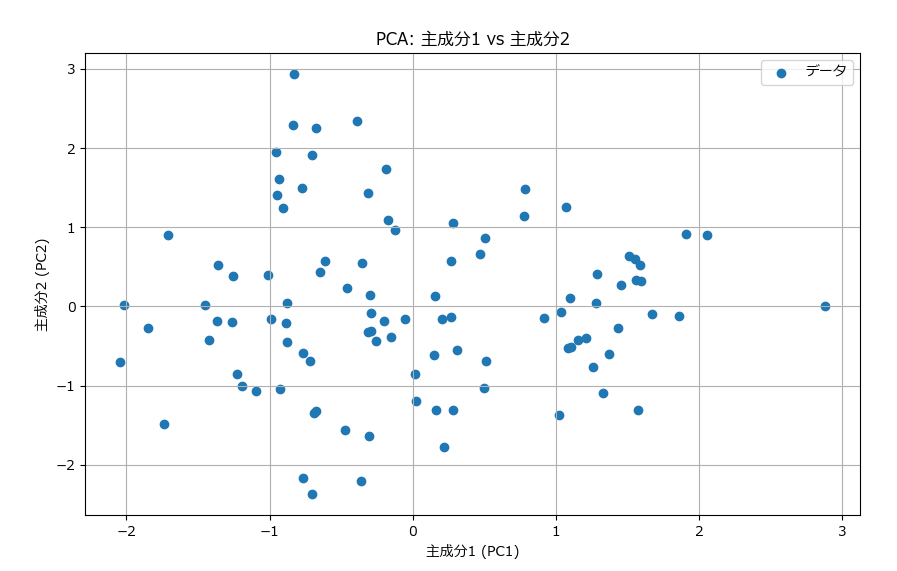
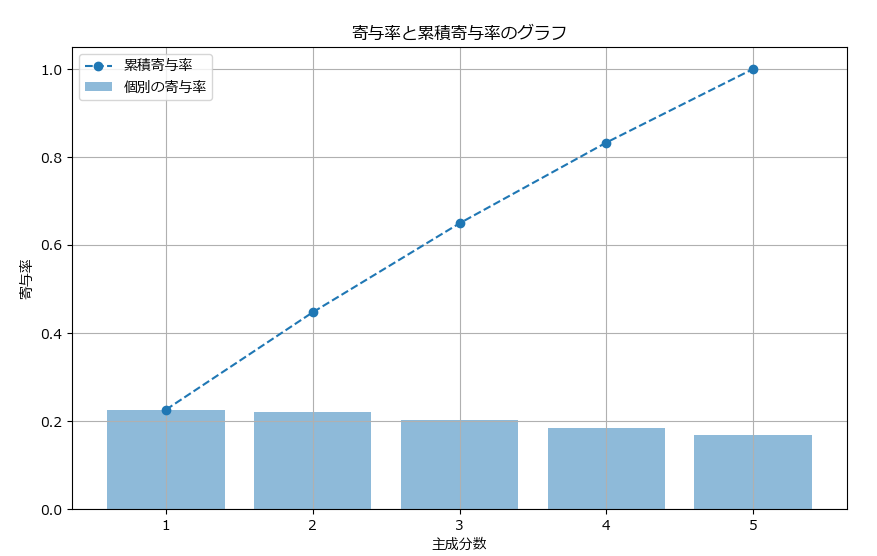
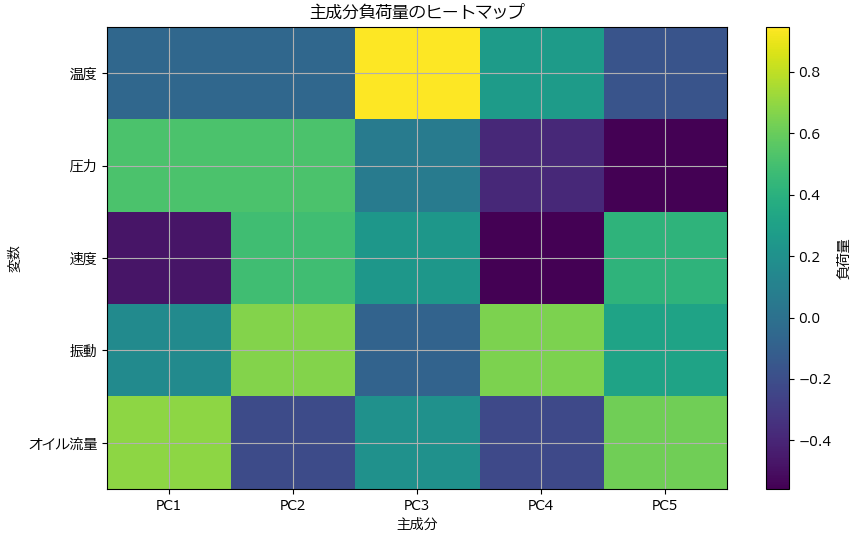
結果の解釈の仕方
寄与度
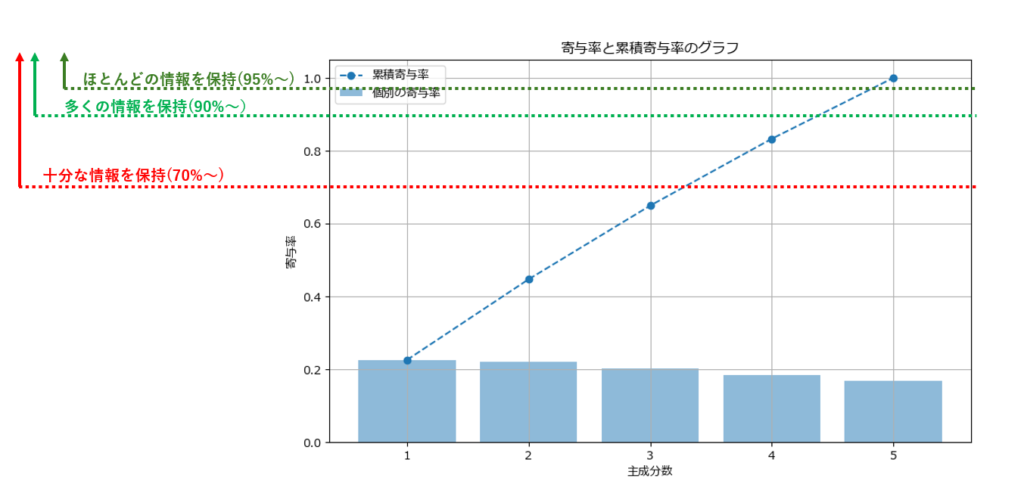
PCAの結果、5つの説明変数が3つの主成分に再編されました。寄与度は、各主成分がデータの全体のばらつき(分散)にどれくらい寄与しているかを示します。これは、各主成分がどれだけ情報を保持しているかを意味しています。
各主成分の寄与率:
[0.22574995 0.2212905 0.20220346]
- PC1の寄与率: 約22.57%
- PC2の寄与率: 約22.13%
- PC3の寄与率: 約20.22%
これらの数値を合わせると、3つの主成分だけで全データの約65%程度のばらつきを説明できることになります。寄与率の目安は70%以上であるため、少し足りないといったところです。
70%を超えるためには、n_componentsに4や5を指定して、主成分の数を増やしてみることも1つの手です。
主成分の負荷量
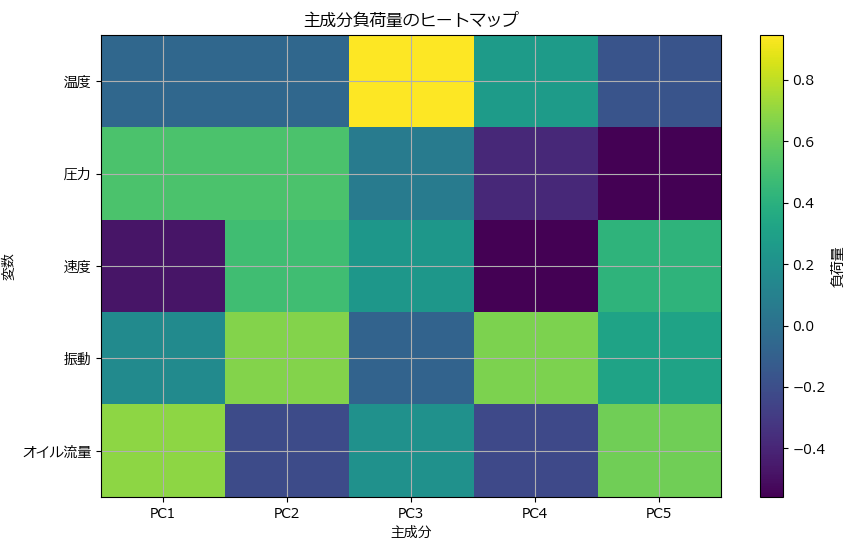
主成分の負荷量(loading)から、各元の説明変数(特徴量)が主成分にどれだけ影響を与えているかが分かります。以下が今回のテストデータから出された負荷量の結果です。
| 特徴量 | PC1 | PC2 | PC3 |
|---|---|---|---|
| 温度 | -0.0534 | -0.0572 | 0.9453 |
| 圧力 | 0.5167 | 0.5194 | 0.0698 |
| 速度 | -0.4745 | 0.4836 | 0.2349 |
| 振動 | 0.1597 | 0.6685 | -0.0789 |
| オイル流量 | 0.6925 | -0.2148 | 0.1999 |
PC1(主成分1)において、数値が高いセンサーは次の3つです。
- オイル流量 (0.6925): PC1は「オイル流量」に強く影響されている。
- 圧力 (0.5167): 圧力もPC1に寄与している。
- 速度 (-0.4745): 速度は負の方向に影響している。
このことから、PC1は「オイル流量」と「圧力」に正の影響を受けており、速度に対しては負の影響を受ける指標だと解釈できます。
PC2(主成分2)において、数値が高いセンサーは次の3つです。
- 負荷量が大きい特徴量:
- 振動 (0.6685): 振動がPC2に強く影響している。
- 圧力 (0.5194): 圧力がPC2に関係している。
- 速度(0.4836): 速度もPC2に関係している。
このことから、PC2は「振動 」、「圧力」、「速度」に正の影響を受ける指標だと解釈できます。
PC3(主成分3)は、「温度」が最も高く、「速度」と「オイル流量」が少しだけ値を持っています。
- 負荷量が大きい特徴量:
- 温度 (0.9453): 温度の影響がPC3の主な要因。
- 速度(0.2349):少し影響する。
- オイル流量(0.1999):少し影響する。
このことから、PC3は「温度 」に強い正の影響を受けるが、「速度」と「オイル流量」についても、わずかながら影響される指標だと解釈できます。
統計学や教育分野の例では、PCAの結果を使って、例えば、「第一主成分」が「言語力の高い人」を表すような意味付けをすることがあります。
これは、主成分が「国語」と「英語」といった言語系科目の点数が関連するパターンを捉えている場合です。
このようにPCAで得られた主成分を専門知識や背景知識を活かして意味づけ(解釈)することが行われます。
主成分分析(PCA)を使う上での注意点
- データの標準化が必要
各特徴量のスケールが異なる場合、大きなスケールを持つ特徴量が主成分を支配してしまいます。そのため、PCAを実行する前にデータを標準化(平均0、分散1)しておくことが重要です。 - スケールの影響を意識する
PCAは線形性に基づく手法であり、データのスケールや分布が結果に影響を及ぼします。非線形な構造が存在する場合、他の次元削減手法も検討してください。 - 次元削減後の情報損失を評価する
主成分をいくつ選ぶかによって保持される情報量が変わります。固有値や寄与率を確認し、目的に応じてバランスの取れた選択をしてください。 - 過剰解釈のリスクに注意
主成分はデータの構造を表しますが、元の特徴量に比べて直接的な意味が失われることがあります。そのため、結果を過剰に解釈しないよう注意してください。 - 可視化を活用する
次元削減後のデータを2Dや3Dで可視化することで、データのクラスターや異常値を視覚的に把握しやすくなります。分析結果の理解を深めるために有効です。 - 目的と結果の整合性を確認
PCAの目的が分析の目的に合致しているかを確認してください。次元削減によって失われた情報が重要な場合、他のアプローチや調整を検討する必要があります。
主成分分析(PCA)の用途別サンプルプログラム
この章で紹介するPCAの応用例をご自身のデータに用いる場合は、必ず負荷量や寄与率を確認し、結果に十分な情報量が含まれているこを確認しておきましょう。例えば圧縮やノイズ削減を行った際、必要な情報まで削ぎ落されている可能性があります。
下記は、本章で紹介するサンプルプログラムに投入するためのデータを作成するプログラムです。
5次元(5つの説明変数)データを生成しています。
# 共通部分: データ準備
import numpy as np
import pandas as pd
# サンプルデータの生成
np.random.seed(42)
data = pd.DataFrame({
'センサー1': np.random.normal(0, 1, 100),
'センサー2': np.random.normal(1, 2, 100),
'センサー3': np.random.normal(-1, 1, 100),
'センサー4': np.random.normal(0.5, 1.5, 100),
'センサー5': np.random.normal(-0.5, 1, 100),
})実行すると data には下記の通り5次元データが生成されます。
センサー1 センサー2 センサー3 センサー4 センサー5
0 0.496714 -1.830741 -0.642213 -0.743493 -2.094428
1 -0.138264 0.158709 -0.439215 -0.340272 -1.099375
~~~中略~~~
98 0.005113 1.116417 -0.187138 0.328190 -1.375618
99 -0.234587 -1.285941 -0.370371 2.356724 -1.882800
PCAを行う場合、データをスケーリングするのが一般的です。
例えば、PCAを使って次元削減やノイズ除去をする場合はスケーリングが必要です。
しかし、データの可視化やモデル前処理の準備においては、スケーリングを必ずしも行う必要はありません。
高次元データの次元削減
高次元データは特徴量(変数)が多すぎて、計算や分析が困難になることがあります。PCAを使用して、データの最も重要な成分を抽出し、次元を削減します。
これにより、データの解釈や可視化が可能になります。
次元削減する場合は n_components に削減後の次元数(1以上の値)を指定します。下記のサンプルでは2を指定しているため、5次元⇒2次元に削減されます。
# 必要なライブラリ
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
# データのスケーリング
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)
# PCAの適用
pca = PCA(n_components=2)
data_pca = pca.fit_transform(data_scaled)
print("元のデータの次元:", data.shape)
print("削減後のデータの次元:", data_pca.shape)
print(data_pca)元のデータの次元: (100, 5)
削減後のデータの次元: (100, 2)
[[-2.2285265 -0.23533666]
[-0.90050257 -0.22733127]
[-0.58561563 1.29368887]
~~~以下省略~~~
データの圧縮
次元削減とデータ圧縮はプログラム的には同じですが、圧縮はなるべく元の情報を残したままデータ量を減らしたいので、次元数が元の次元数より減っていさえすれば、それが何次元になろうが構いません。
データ圧縮では、圧縮後にどれくらい情報を残しておきたいかが重要なので、n_componentsに寄与率の合計(分散を保持する割合)を 0~0.99 の間で指定します。
PCA()は、n_components の値が1以上の場合は次元数が、1未満の場合は分散の割合が指定されたと解釈して動作します。
寄与率の合計が90%~95%であれば、元の情報が十分に含んでいることになるので、0.9や0.95を指定するケースが多いですが、今回のサンプルデータでは圧縮できません(次元数が元と同じ)でした。そこで、下記プログラムでは 0.86 を指定したことろ、次元数が1つ減り(圧縮された)、4次元となりました。
# 必要なライブラリ
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
# データのスケーリング
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)
# PCAで95%の分散を保持
pca = PCA(n_components=0.86)
data_reduced = pca.fit_transform(data_scaled)
print("元のデータの次元:", data.shape)
print("圧縮後のデータの次元:", data_reduced.shape)
print(data_reduced)元のデータの次元: (100, 5)
圧縮後のデータの次元: (100, 4)
[[-2.22852650e+00 -2.35336659e-01 -9.63616720e-01 -1.19985559e-01]
[-9.00502573e-01 -2.27331268e-01 -1.04564699e-01 -3.60992433e-01]
~~~以下省略~~~
寄与率の合計を指定した場合、それを保持するために必要な次元数に次元圧縮されるため、データによっては圧縮前と圧縮後の次元数が変わらない(つまり、圧縮できなかった)場合があります。
ノイズの除去
主成分の寄与度が高いものが重要であることの裏返しとして、寄与度の低いものはノイズ成分であると考えた場合、寄与度の低いものを除外することでノイズ除去ができます。
従って、次元削減やデータ圧縮と同じプログラムにはなりますが、n_componentsに指定する値が異なります。
ノイズ削減はデータ品質を高めるために、できるだけ多くノイズ除去したい訳ですから、次元数ではなく寄与度の合計を指定し、その値もデータ圧縮より低めの%0.7~0.8%を狙うのが一般的です。
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
# データのスケーリング
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)
# PCAの適用(80%の分散を保持)
pca = PCA(n_components=0.7)
data_reduced = pca.fit_transform(data_scaled)
print("元のデータの次元:", data.shape)
print("ノイズの除去の次元:", data_reduced.shape)
元のデータの次元: (100, 5)
圧縮後のデータの次元: (100, 3)
[[-2.2285265 -0.23533666 -0.96361672]
[-0.90050257 -0.22733127 -0.1045647 ]
~~~以下省略~~~
データの可視化
4次元以上のデータは可視化できないため、2次元又は3次元に変換することで可視化できるようになります。
# 必要なライブラリ
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
# PCAの適用(スケーリングなし)
pca = PCA(n_components=2)
data_pca = pca.fit_transform(data)
# 可視化
plt.figure(figsize=(8, 6))
plt.scatter(data_pca[:, 0], data_pca[:, 1], c='blue', alpha=0.6)
plt.title('PCAによる2次元可視化(スケーリングなし)')
plt.xlabel('主成分1')
plt.ylabel('主成分2')
plt.grid()
plt.show()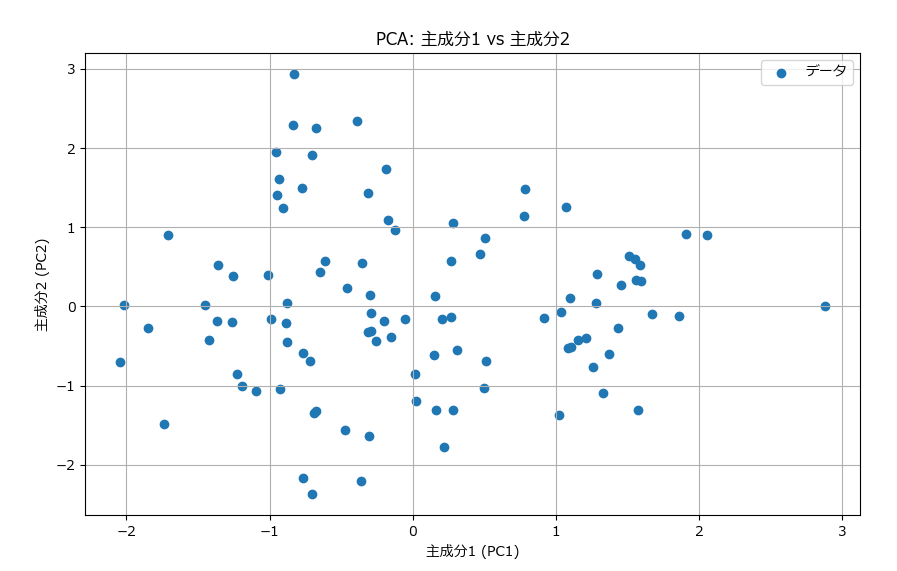
特徴量選択の効率化(スケーリングなし)
PCAの結果出力される寄与率は、各目的変数(各特徴量)がどのていど寄与しているかを表しているため、寄与率の大きいものを選ぶことで、特徴量選択ができます。尚、この場合はスケーリングの必要は特にありません。
# 必要なライブラリ
from sklearn.decomposition import PCA
# PCAの適用(すべての成分を考慮)
pca = PCA(n_components=None)
pca.fit(data)
# 特徴量ごとの寄与率
print("各特徴量の寄与率:")
print(pd.DataFrame({
'特徴量': data.columns,
'寄与率': pca.explained_variance_ratio_
}))特徴量 寄与率
0 センサー1 0.436593
1 センサー2 0.225978
2 センサー3 0.147440
3 センサー4 0.108400
4 センサー5 0.081589
異常検知(スケーリングが必要)
異常検知は再構成誤差を使います。元のデータで作成したPCAのモデル(元のデータの主要なパターンや特性を捉えたモデル)に対して新しいデータを投入すると、次元削減されます。これを再構成して元に戻すと、誤差がほとんど発生しないはずです。もし誤差が発生するならば、それはモデル作成時とは異なる分布のデータ=異常データと判断します。
下記サンプルプログラムでは、前述のテストデータで作成したモデルに対して、10個のデータを生成し、異常検知を行っています。
from sklearn.decomposition import PCA
import pickle
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
# ------------------------------------------------
# 正常データを用いたモデルの作成
# ------------------------------------------------
# PCAの適用
pca = PCA(n_components=2)
pca.fit(data)
# モデルの保存
with open('pca_model.pkl', 'wb') as f:
pickle.dump(pca, f)
# ------------------------------------------------
# 新しいデータで異常検知を実施
# ------------------------------------------------
# 新しいデータの生成
new_data = pd.DataFrame({
'センサー1': np.random.rand(10), # 特徴量名を元のデータと一致させる
'センサー2': np.random.rand(10),
'センサー3': np.random.rand(10),
'センサー4': np.random.rand(10),
'センサー5': np.random.rand(10)
})
# PCAモデルの読み込み
with open('pca_model.pkl', 'rb') as f:
loaded_pca = pickle.load(f)
# 新しいデータをPCAモデルで変換
transformed_new_data = loaded_pca.transform(new_data)
# 新しいデータの再構成
reconstructed_data = loaded_pca.inverse_transform(transformed_new_data)
# 再構成誤差の計算(※1)
reconstruction_error = np.mean((new_data.values - reconstructed_data)**2, axis=1)
# 再構成誤差の閾値設定(※2)。平均値に標準偏差の3倍(3σ)を加えたもの
threshold = reconstruction_error.mean() + 3 * reconstruction_error.std()
# 誤差(※1)が閾値(※2)を超えているかで異常を判定
is_anomalous = reconstruction_error > threshold
print("新しいデータの再構成誤差:")
print(reconstruction_error)
print("\n異常検知の結果(True = 異常, False = 正常):")
print(is_anomalous)
# 可視化
plt.figure(figsize=(10, 6))
plt.hist(reconstruction_error, bins=30, alpha=0.5, label='新しいデータの再構成誤差')
plt.axvline(threshold, color='r', linestyle='--', label='異常検知の閾値')
plt.xlabel('再構成誤差')
plt.ylabel('頻度')
plt.legend()
plt.title('新しいデータの再構成誤差の分布')
plt.grid()
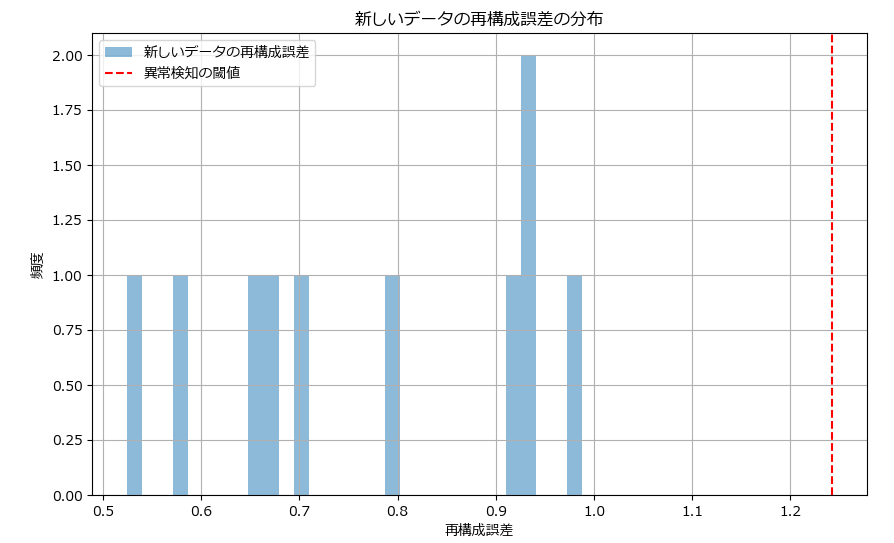
plt.show()今回は10個のデータを投入したので、10個分の判定結果が出力されています。いずれも正常の範囲でした。
新しいデータの再構成誤差:
[0.93145552 0.98777348 0.93408416 0.58119932 0.52473326 0.6494172
0.79979233 0.9181818 0.67311155 0.70048575]
異常検知の結果(True = 異常, False = 正常):
[False False False False False False False False False False]
下記は10個のデータにおける再構成誤差のヒストグラムです。赤の点線は異常検知の閾値(平均+3σ)です。異常データがあれば、赤い点線の右にデータ(棒グラフ)に表示されます。
モデルの前処理(スケーリングが必要)
次元削減されたデータをモデルの入力として使用することで、計算効率の向上と過学習の抑制が行えます。下記、次元削減した結果をランダムフォレストの分類モデルで学習させるサンプルプログラムです。
# 必要なライブラリ
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# ラベルを仮定
np.random.seed(42)
labels = np.random.choice([0, 1], size=100)
# データのスケーリング
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)
# PCAによる次元削減
pca = PCA(n_components=2)
data_pca = pca.fit_transform(data_scaled)
#-------------------------------------------------------------------------
# 以下は、次元圧縮した結果を使って、ランダムフォレストのモデルを作成するサンプル
#-------------------------------------------------------------------------
# 学習データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(data_pca, labels, test_size=0.2, random_state=42)
# モデルの学習
model = RandomForestClassifier(random_state=42)
model.fit(X_train, y_train)
# モデルの評価
y_pred = model.predict(X_test)
print("モデルの精度:")
print(accuracy_score(y_test, y_pred))モデルの精度:
0.45
主成分分析(PCA)が簡単に行える自作クラス
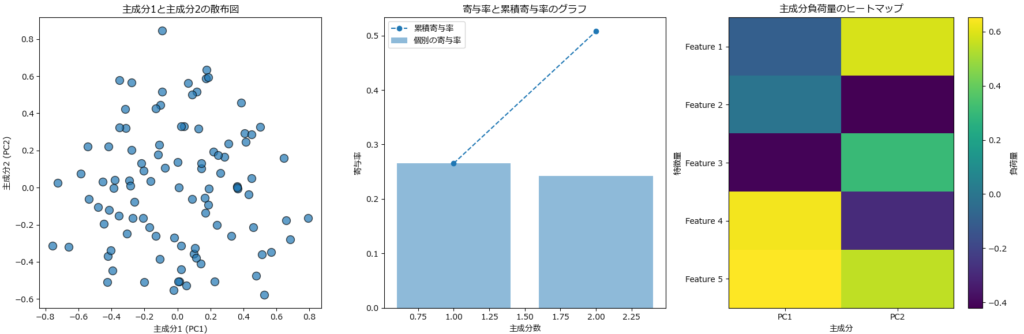
PCAとグラフ化が簡単に行える関数とクラスを作ったので紹介します。使い方は次の通りです。
次元削減/データ圧縮/ノイズ除去/特徴量選択など(異常検知以外)
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# ここに後述するグラフ描画関数とPCAUtilクラスを張り付けるか、インポートしてください。
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# データの生成
np.random.seed(42)
data = pd.DataFrame({
'feature1': np.random.rand(100),
'feature2': np.random.rand(100),
'feature3': np.random.rand(100),
'feature4': np.random.rand(100),
'feature5': np.random.rand(100)
})
# PCAモデルの作成と学習
pca_util = PCAUtil(df=data)
pca_util.fit(columns=['feature1', 'feature2', 'feature3', 'feature4', 'feature5'])
print("変換されたデータ:")
print(pca_util.transformed_data)
# 寄与率の取得
print("寄与率:")
print(pca_util.explained_variance_ratio)
print("負荷量")
print(pca_util.loadings)
# グラフの描画
plot_pca_results(pca_util)変換されたデータ:
[[-1.86487044 -0.29761243]
[ 0.85937956 1.21562567]
~~中略~~
[ 1.55533059 -0.29714907]
[ 2.4139103 -0.12472002]]
寄与率:
[0.2654305 0.24233576]
負荷量
PC1 PC2
feature1 -0.299147 0.467990
feature2 0.164928 -0.533742
feature3 -0.533414 0.098370
feature4 0.709334 0.094175
feature5 0.309232 0.691057
異常検知
異常検知のサンプルプログラムは、5個の説明変数を使ってPCAモデルを作成し、10個のテストデータを使って異常検知をしています。PCAのモデルはファイルに保存し、異常検知の際には読み込んだモデルを使っています。
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# ここに後述するグラフ描画関数とPCAUtilクラスを張り付けるか、インポートしてください。
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# ステップ1: データの生成
np.random.seed(42)
data = pd.DataFrame({
'feature1': np.random.rand(100),
'feature2': np.random.rand(100),
'feature3': np.random.rand(100),
'feature4': np.random.rand(100),
'feature5': np.random.rand(100)
})
# ステップ2: PCAモデルの作成と学習
pca_util = PCAUtil(df=data)
pca_util.fit(columns=['feature1', 'feature2', 'feature3', 'feature4', 'feature5'])
# モデルの保存
model_path = 'pca_model.pkl'
pca_util.save_model(model_path)
# ステップ3: 新しいデータの生成
new_data = pd.DataFrame({
'feature1': np.random.rand(100),
'feature2': np.random.rand(100),
'feature3': np.random.rand(100),
'feature4': np.random.rand(100),
'feature5': np.random.rand(100)
})
# 新しいデータをPCAUtilクラスに設定
pca_util_new = PCAUtil(df=new_data)
# 保存したモデルの読み込み
pca_util_new.load_model(model_path)
# ステップ4: 異常検知
anomalies, reconstruction_error, threshold = pca_util_new.detect_anomalies(
columns=['feature1', 'feature2', 'feature3', 'feature4', 'feature5'])
# ステップ5: 結果の表示
print("再構成誤差:")
print(reconstruction_error)
print("\n異常検知の結果(True = 異常, False = 正常):")
print(anomalies)
print("\n異常検知の閾値:")
print(threshold)
# ステップ6: グラフの描画
plot_pca_results(pca_util_new)
plot_reconstruction_error_hist(reconstruction_error, threshold)再構成誤差:
[0.05838233 0.09376962 0.04509941 0.06463465 0.07826037 0.0902368
~~中略~~
0.02472335 0.01817293 0.0166673 0.01711131 0.11745507 0.00572071
0.01650207 0.02698277 0.09417168 0.06690861]
異常検知の結果(True = 異常, False = 正常):
[False False False False False False False False False False False False
~~中略~~
False False False False False False False False False False False False
False False False False]
異常検知の閾値:
0.14013297328493077
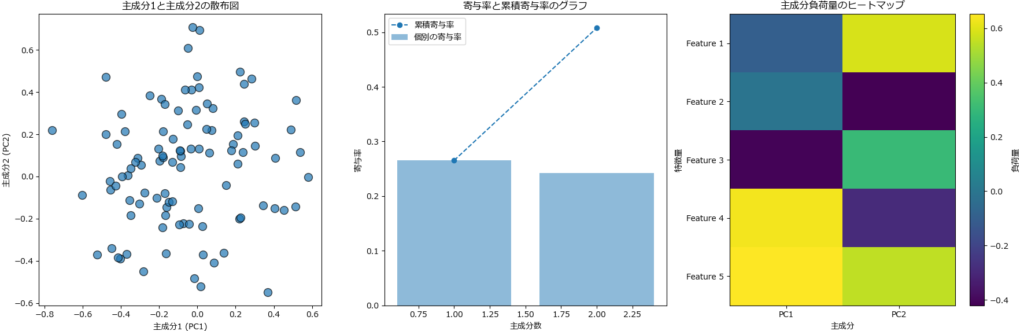
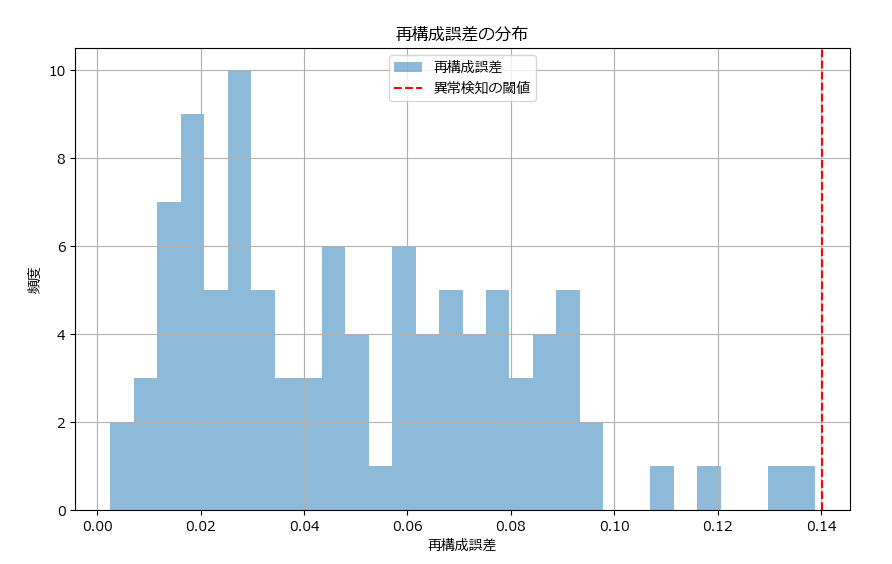
グラフ描画関数のソースコード
| 関数名 | 説明 | パラメーター | 戻り値 |
|---|---|---|---|
| plot_pca_results | PCAの結果をプロットする関数。 | pca: 学習済みのPCAモデル | なし |
| plot_reconstruction_error_hist | 再構成誤差のヒストグラムをプロットする関数。 | reconstruction_error : 再構成誤差の配列threshold : 異常検知の閾値。 | なし |
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import rcParams
from sklearn.decomposition import PCA
rcParams['font.family'] = 'Meiryo'
# PCAの結果をプロットする関数
def plot_pca_results(pca):
"""
PCAの結果をプロットする関数。
Parameters:
pca : PCA
学習済みのPCAモデル。
"""
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
# PC1 vs PC2の散布図
scatter = axes[0].scatter(pca.transformed_data[:, 0], pca.transformed_data[:, 1], alpha=0.7, edgecolors='k', s=100)
axes[0].set_xlabel('主成分1 (PC1)')
axes[0].set_ylabel('主成分2 (PC2)')
axes[0].set_title('主成分1と主成分2の散布図')
# 寄与率と累積寄与率の棒グラフと折れ線グラフの組み合わせ
cumulative_explained_variance = np.cumsum(pca.explained_variance_ratio)
axes[1].bar(range(1, len(pca.explained_variance_ratio) + 1), pca.explained_variance_ratio, alpha=0.5, align='center', label='個別の寄与率')
axes[1].plot(range(1, len(cumulative_explained_variance) + 1), cumulative_explained_variance, marker='o', label='累積寄与率', linestyle='--')
axes[1].set_xlabel("主成分数")
axes[1].set_ylabel("寄与率")
axes[1].set_title("寄与率と累積寄与率のグラフ")
axes[1].legend()
# 主成分負荷量のヒートマップ
cax = axes[2].imshow(pca.loadings, cmap='viridis', aspect='auto')
plt.colorbar(cax, ax=axes[2], orientation='vertical', label='負荷量')
axes[2].set_xticks(np.arange(pca.n_components))
axes[2].set_xticklabels([f"PC{i+1}" for i in range(pca.n_components)])
axes[2].set_yticks(np.arange(len(pca.columns)))
axes[2].set_yticklabels([f"Feature {i+1}" for i in range(pca.df.shape[1])])
axes[2].set_xlabel("主成分")
axes[2].set_ylabel("特徴量")
axes[2].set_title("主成分負荷量のヒートマップ")
plt.tight_layout()
plt.show()
# 再構成誤差のヒストグラムをプロットする関数
def plot_reconstruction_error_hist(reconstruction_error, threshold):
"""
再構成誤差のヒストグラムをプロットする関数。
Parameters:
reconstruction_error : array-like
再構成誤差の配列。
threshold : float
異常検知の閾値。
"""
plt.figure(figsize=(10, 6))
plt.hist(reconstruction_error, bins=30, alpha=0.5, label='再構成誤差')
plt.axvline(threshold, color='r', linestyle='--', label='異常検知の閾値')
plt.xlabel('再構成誤差')
plt.ylabel('頻度')
plt.legend()
plt.title('再構成誤差の分布')
plt.grid()
plt.show()主成分分析(PCA)便利クラスのソースコード
| メソッド名 | 説明 | パラメーター | 戻り値 |
|---|---|---|---|
| __init__ | PCAUtilクラスの初期化メソッド。 | df : 分析に使用するデータフレーム (オプション) model_path : 保存済みPCAモデルのパス (オプション) | なし |
| fit | PCAモデルの作成と学習を行うメソッド。 | columns : PCAを適用するデータフレームのカ ラム名のリスト n_components : PCAで抽出する主成分の数 (デフォルトは2) scale : スケーリングの指定 (デフォルトはTrue) | PCA |
| transform | 学習済みモデルを使用してデータを変換するメソッド。 | columns : 変換するデータフレームのカラム名のリスト(省略するとモデル作成時に指定したカラム名のリストが使用される) scale : スケーリングの指定 (デフォルトはTrue) | numpy.ndarray |
| read_csv | CSVファイルを読み込むメソッド。 | file_name : 読み込むCSVファイルのパスencoding : ファイルのエンコーディング (デフォルトは"shift-jis") | なし |
| save_model | PCAモデルをファイルに保存するメソッド。 | model_path : 保存するファイルのパス。 | なし |
| load_model | 保存済みPCAモデルを読み込むメソッド。 | model_path : 読み込むPCAモデルのファイルのパス(デフォルトはNone) | PCA |
| detect_anomalies | データの異常検知を行うメソッド。 | columns : 異常検知を行うデータフレームのカラム名のリスト (省略すると、fitまたはtransformで指定したカラム名のリストが使用される)threshold : 異常とみなす再構成誤差の閾値(デフォルトはNoneで、再構成誤差の平均 + 3 * 標準偏差が設定される) scale : スケーリングの指定 (デフォルトはTrue) | tuple : 異常フラグの配列、再構成誤差の配列、閾値。 |
import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import pickle
# PCAUtilクラス
class PCAUtil:
def __init__(self, df=None, model_path=None):
"""
PCAUtilクラスの初期化メソッド。
Parameters:
df : pandas.DataFrame, optional
分析に使用するデータフレーム。デフォルトはNone。
model_path : str, optional
保存済みPCAモデルのパス。デフォルトはNone。
"""
self.df = None if df is None else df.copy()
self.model = None if model_path is None else self.load_model(model_path)
self.transformed_data = None # PCAで変換されたデータ
self.explained_variance_ratio = None # PCAの寄与率
self.loadings = None # 負荷量
self.n_components = None # 主成分の数
self.columns = []
self.scaler = StandardScaler()
def fit(self, columns, n_components=2, scale=True):
"""
PCAモデルの作成と学習を行うメソッド。
Parameters:
columns : list of str
PCAを適用するデータフレームのカラム名のリスト。
n_components : int, optional
PCAで抽出する主成分の数。デフォルトは2。
scale : bool, optional
データをスケーリングするかどうか。デフォルトはTrue。
Returns:
PCA
学習済みのPCAモデル。
"""
self.columns = columns
X = self.df[columns].values
if scale:
X = self.scaler.fit_transform(X)
self.model = PCA(n_components=n_components).fit(X)
self.transform(columns, scale=scale)
return self.model
def transform(self, columns=None, scale=True):
"""
学習済みモデルを使用してデータを変換するメソッド。
Parameters:
columns : list of str
変換するデータフレームのカラム名のリスト。
省略するとモデル作成時に指定したカラム名のリストが使用される。
scale : bool, optional
データをスケーリングするかどうか。デフォルトはTrue。
Returns:
numpy.ndarray
変換されたデータ。
"""
if columns is None:
columns = self.columns
else:
self.columns = columns
X = self.df[columns].values
if scale:
X = self.scaler.fit_transform(X)
self.transformed_data = self.model.transform(X)
self.explained_variance_ratio = self.model.explained_variance_ratio_
self.n_components = self.model.n_components_
self.loadings = pd.DataFrame(self.model.components_.T,
index=self.columns, columns=[f"PC{i+1}" for i in range(self.n_components)])
return self.transformed_data
def read_csv(self, file_name, encoding="shift-jis"):
"""
CSVファイルを読み込むメソッド。
Parameters:
file_name : str
読み込むCSVファイルのパス。
encoding : str, optional
ファイルのエンコーディング。デフォルトは"shift-jis"。
"""
self.df = pd.read_csv(file_name, encoding=encoding)
def save_model(self, model_path):
"""
PCAモデルをファイルに保存するメソッド。
Parameters:
model_path : str
保存するファイルのパス。
"""
self.model_path = model_path
with open(model_path, 'wb') as f:
pickle.dump(self.model, f)
def load_model(self, model_path=None):
"""
保存済みPCAモデルを読み込むメソッド。
Parameters:
model_path : str, optional
読み込むPCAモデルのファイルのパス。デフォルトはNone。
Returns:
PCA
読み込まれたPCAモデル。
"""
model_path = model_path if model_path else self.model_path
with open(model_path, 'rb') as f:
self.model = pickle.load(f)
return self.model
def detect_anomalies(self, columns=None, threshold=None, scale=True):
"""
データの異常検知を行うメソッド。
Parameters:
columns : list of str
異常検知を行うデータフレームのカラム名のリスト。
省略すると、fit 又は transform で指定したカラム名のリストが使用される。
threshold : float, optional
異常とみなす再構成誤差の閾値。デフォルトはNoneで、
再構成誤差の平均 + 3 * 標準偏差が設定されます。
scale : bool, optional
データをスケーリングするかどうか。デフォルトはTrue。
Returns:
tuple
異常フラグの配列、再構成誤差の配列、閾値。
"""
# データを変換
columns = self.columns if columns is None else columns
self.transform(columns, scale=scale)
# 再構成
reconstructed_data = self.model.inverse_transform(self.transformed_data)
if scale:
reconstructed_data = self.scaler.inverse_transform(reconstructed_data)
# 再構成誤差を計算
reconstruction_error = np.mean((self.df[columns].values - reconstructed_data)**2, axis=1)
# 閾値を設定(デフォルトは再構成誤差の平均 + 3 * 標準偏差)
if threshold is None:
threshold = reconstruction_error.mean() + 3 * reconstruction_error.std()
# 異常検知
anomalies = reconstruction_error > threshold
return anomalies, reconstruction_error, thresholdまとめ
本記事では、主成分分析について、基本的な使い方と応用例について、ソースコードを交えて詳しく解説しました。
主成分分析(PCA)の効果は、データに含まれる情報をできるだけ保持したまま、複数の説明変数を統合(=次元削減)する手法です。
そして、この方法を応用することで、次元削減、データ圧縮、ノイズ除去、可視化、異常検知、特徴量選択、モデルの前処理に絶大な効果を発揮してくれます。
もし、これからPCAを仕事で使われる方は、是非この記事を参考にしてください。









コメント