機械学習モデルを開発する際、その性能を評価する指標を正しく選ぶことは非常に重要です。同じモデルでも、評価指標によって「優れたモデル」と評価されるかどうかが大きく変わることがあります。
例えば、製造業における設備異常の検知モデルでは、Precision(適合率)が重視されることが多いです。誤検知を減らすことで、不要な停止やコストの増大を防ぐためです。一方、製品検査工程ではAccuracy(正確率)が重要視される場合があり、全体的な検査精度が効率向上に直結します。
本記事では、これらの評価指標の基本的な概念について、Pythonのソースコードを交えながら解説します。
また、今回紹介する評価指標とグラフが簡単に出力できる自作関数も用意しました。
実務でモデル評価がしたいが、どうすれば良いか困っている方は、ぜひご一読ください。
分類モデルにおける評価指標の概要
分類モデルの評価指標は、機械学習で作成したモデルがどれだけ正確に目的に応じた分類を行えるかを測定するための基準です。モデルの性能を客観的に比較・評価し、最適なモデルを選択するために使用されます。
分類タスクの結果は通常、正解か不正解かの2値(あるいは多値)で示されるため、その結果を基に計算されるさまざまな指標が存在します。
以下は分類モデルにおける評価指標の一覧です。
| 指標 | 意味 | 特徴 | 適用例 |
|---|---|---|---|
| Accuracy | 全体の予測のうち正しく分類された割合 | クラスの分布が均一な場合に有効。ただし、不均一データでは注意が必要。 | 製品分類、正常状態の判別 |
| Precision | モデルが「正例」と予測した中で、実際に正例であった割合 | 誤検知(偽陽性)を避けたい場合に重視。 | 異常検知、欠陥品の検出 |
| Recall | 実際に正例であるもののうち、正しく正例と予測された割合 | 見逃し(偽陰性)を避けたい場合に重要。 | 故障検知、品質問題の発見 |
| F1スコア | PrecisionとRecallの調和平均 | PrecisionとRecallのバランスを考慮。偏ったデータでも適切に評価可能。 | 欠陥検出の総合評価 |
| ROC曲線 | さまざまな閾値でのTrue Positive RateとFalse Positive Rateの関係を表す曲線 | モデルの識別能力を視覚的に評価。 | 全体的なモデル性能の比較 |
| AUC | ROC曲線の下の面積 | 値が1に近いほど性能が高い。複数モデルの総合評価に便利。 | モデル全体の性能比較 |
評価指標の説明
正確度 (Accuracy)

正確度は、正しく予測されたサンプルの割合を示します。簡単な指標であるため、データのクラスバランスが取れていない場合には適していません。
クラスバランスとは、分類タスクにおける各クラスのサンプル数の比率を指します。もし、あるクラスが他のクラスに比べて圧倒的に多い、または少ない場合、その問題を「クラス不均衡」または「クラスバランスの不均衡」と呼びます。
from sklearn.metrics import accuracy_score
# 精度の計算(y_test:テストデータ, y_pred:予測データ)
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy}")Accuracy: 0.925
「クラス不均衡」の場合、モデルは多数派クラスに偏って学習するため、少数派クラスの予測が誤って分類されやすくなります。しかし、Accuracy(正確度)は全体の正しい予測を基に計算されるため、多数派クラスの予測結果が大きく影響し、少数派クラスの予測性能が表面上は反映されません。
混同行列 (Confusion Matrix)
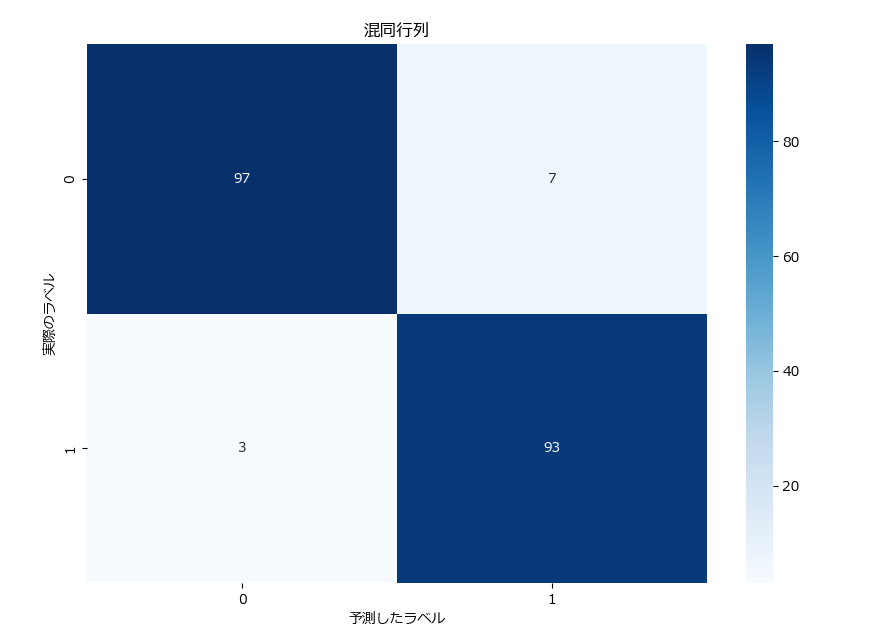
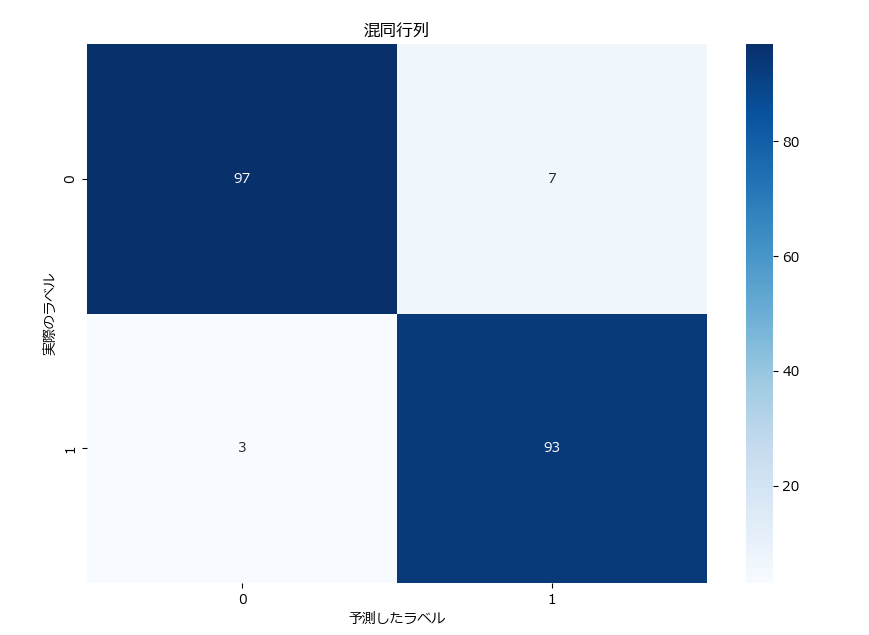
混同行列は、モデルの予測結果を具体的に分析するために使用されます。各クラスの真陽性 (TP)、偽陰性 (FN)、偽陽性 (FP)、真陰性 (TN) をマトリクス表として表します。
| 実際の正 (Positive) | 実際の負 (Negative) | |
|---|---|---|
| 予測の正 (Positive) | 真陽性 (TP) | 偽陽性 (FP) |
| 予測の負 (Negative) | 偽陰性 (FN) | 真陰性 (TN) |
下記は混同行列の表示とヒートマップを使った可視化のサンプルです。
from sklearn.metrics import confusion_matrix
# 混同行列(y_test:テストデータ, y_pred:予測データ)
cm = confusion_matrix(y_test, y_pred))
# 混同行列を表示する
print(cm)
# 混同行列を可視化する
plt.figure(figsize=(10, 7))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues')
plt.xlabel('予測したラベル')
plt.ylabel('実際のラベル')
plt.title('混同行列')
plt.show()[[97 7]
[ 3 93]]
可視化することで直感的に分かり易くなります。
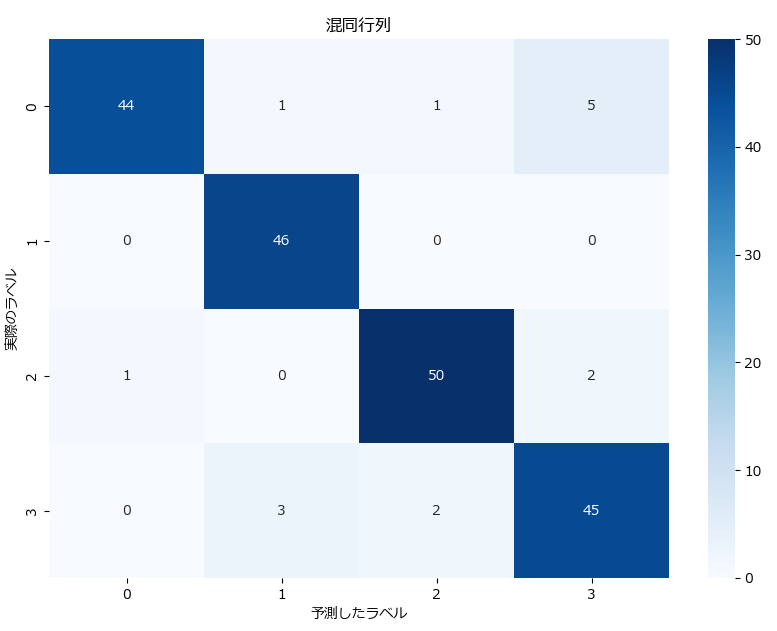
多値分類の混同行列は、クラス数 × クラス数の正方形の行列で表されます。
例:4クラス分類の場合の混同行列
| 実際 \ 予測 | クラス0 | クラス1 | クラス2 |
|---|---|---|---|
| クラス0 | TP (0,0) | FP (0,1) | FP (0,2) |
| クラス1 | FN (1,0) | TP (1,1) | FP (1,2) |
| クラス2 | FN (2,0) | FN (2,1) | TP (2,2) |
| クラス3 | FN (3,0) | FN (3,1) | TP (3,2) |
下記は4クラス分類の出力結果です。
[[44 1 1 5]
[ 0 46 0 0]
[ 1 0 50 2]
[ 0 3 2 45]]
精度 (Precision) と 再現率 (Recall)
混同行列の結果を元に、精度と再現性を算出します。両者の算出式は非常に似通っていますが、精度は分母にFP(負を正として予測した数)を加算しているのに対し、再現率はFN(正を負と予測した数)を加算している点が異なります。
精度 (Precision): 精度は、モデルが「正例」と予測したもののうち、実際に正しいものの割合を示します。
簡単に言うと、「正例を予測した中で、正解だったものの割合=正しく分類できた割合」を表します。
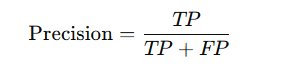
- TP (True Positive)
実際が正のものを、モデルが正と予測したデータ数 - FP (False Positive)
実際には負であるが、モデルが正と予測したデータ数
再現率 (Recall): 再現率は、実際に正しいサンプルのうち、モデルが「正」と予測した割合を示します。
簡単に言うと、「実際に正例であったものをどれだけ正しく予測できたか=取りこぼさなかった割合」を表します。
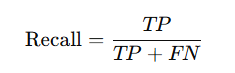
- TP (True Positive)
実際が正のものを、モデルが正と予測したデータ数 - FN (False Negative)
実際に正であるが、モデルが負と予測したデータ数
再現率は、実際に「正例」として分類すべきデータ(False Negative)が漏れた場合に低くなります。例えば、設備の異常検知において、実際に異常が発生している機械や設備を「正常」と予測してしまうと、再現率が低くなります。
下記は、多値分類にも対応したPrecisionとRecallの出力サンプルです。
from sklearn.metrics import classification_report
# classification_report を使って評価結果を取得
report = classification_report(y_test, y_pred, output_dict=True)
# 各クラスごとにPrecisionとRecallを取得
for class_label in report:
if class_label.isdigit(): # クラスが整数である場合
precision = report[class_label]['precision']
recall = report[class_label]['recall']
print(f"Class {class_label} - Precision: {precision}, Recall: {recall}")F1スコア (F1 Score)
混同行列の結果を元に、F1スコアを計算します。
F1スコアは、精度と再現率の調和平均です。F1スコアは、精度と再現率のトレードオフを考慮して、両者のバランスを取る指標として使われます。
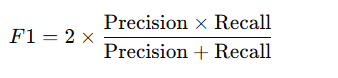
精度が高くても、再現率が低ければ、F1スコアは低くなります。同様に、再現率が高くても精度が低ければ、F1スコアも低くなります。
F1スコアは、不均衡データセットの場合にも役立ちます。例えば、異常検知や医療診断のように、正例(Positive)が少ない場合、精度だけではモデルの評価が不十分になることがありますが、F1スコアはそのバランスを取るため、より正確なモデル評価が可能になります。
下記は、多値分類にも対応したPrecisionとRecallの出力サンプルです。
from sklearn.metrics import classification_report
# classification_report を使って評価結果を取得
report = classification_report(y_test, y_pred, output_dict=True)
# クラスごとにF1スコアを表示
for class_label in report:
if class_label.isdigit(): # クラスが整数である場合
f1_score = report[class_label]['f1-score']
print(f"Class {class_label}: F1-score = {f1_score}")ROC曲線 (ROC Curve) と AUC (Area Under the Curve)
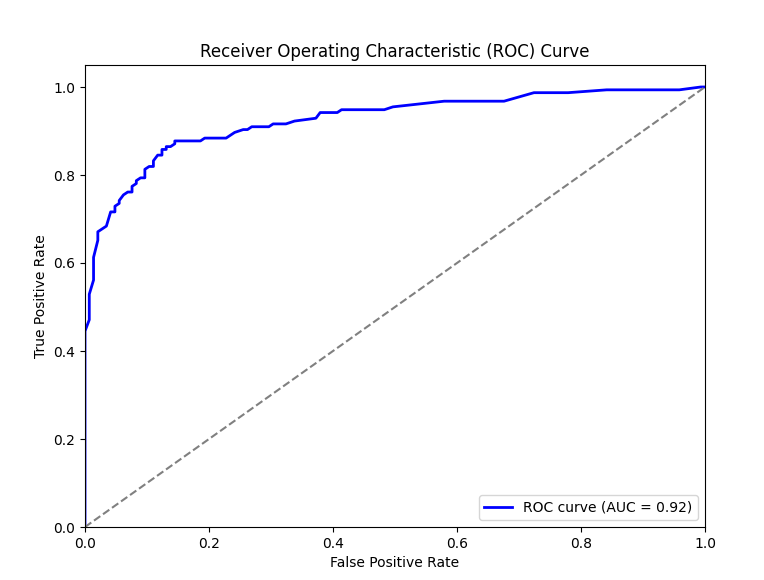
良い例
悪い例
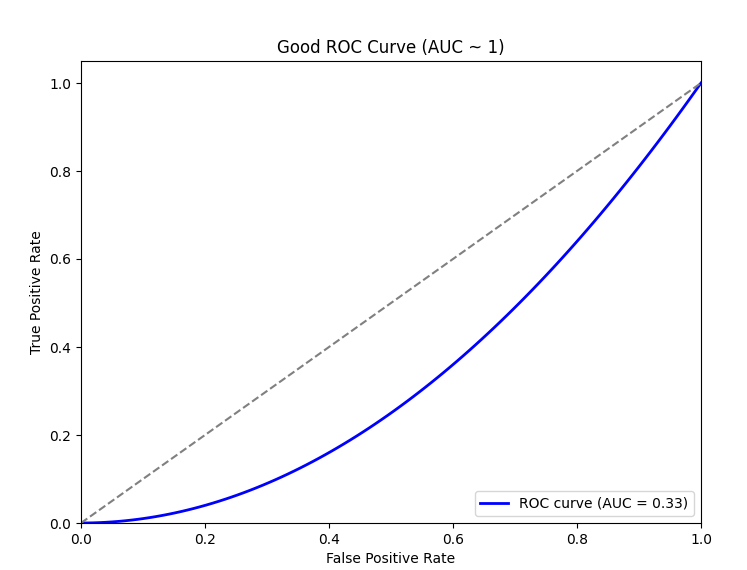
ROC曲線(Receiver Operating Characteristic Curve)は、二項分類モデルの性能を評価するためのグラフです。簡単に言うと、モデルがどれだけ正しく「陽性」を予測できるかを示すものです。
横軸 (x軸): 偽陽性率 (FPR) — 実際には「陰性(0)」なのに、モデルが「陽性(1)」と予測した割合。縦軸 (y軸): 真陽性率 (TPR) — 実際に「陽性(1)」なのに、モデルが「陽性(1)」と予測した割合。
- 曲線が左上に近いほど、良いモデルです(TPRが高く、FPRが低い)
- AUC(曲線下面積)は、ROC曲線の性能を数値で示したもので、AUCが大きいほどモデルの性能が良いと言えます。
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc
# ROC曲線の計算
fpr, tpr, thresholds = roc_curve(y_test, y_prob)
roc_auc = auc(fpr, tpr) # AUCの計算
# ROC曲線のプロット
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='blue', lw=2, label=f'ROC curve (AUC = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='gray', linestyle='--') # ランダム予測線
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic (ROC) Curve')
plt.legend(loc="lower right")
plt.show()評価指標の具体例
下記のプログラムはランダムフォレストを使って精度指標を求めたサンプルです。
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc, accuracy_score, classification_report, confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification
from sklearn.ensemble import RandomForestClassifier
import matplotlib
# 日本語フォントの設定
matplotlib.rcParams['font.family'] = 'Meiryo' # メイリオを指定
# サンプルデータの作成(バイナリ分類)
X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)
# データをトレーニングセットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# ランダムフォレストモデルの訓練
model = RandomForestClassifier(n_estimators=100, random_state=42)
model.fit(X_train, y_train)
# 予測
y_pred = model.predict(X_test)
y_prob = model.predict_proba(X_test)[:, 1] # 陽性クラスの確率
# 精度の計算
accuracy = accuracy_score(y_test, y_pred)
print(f"正確度 (Accuracy): {accuracy * 100:.2f}%")
# 分類レポート
report = classification_report(y_test, y_pred, output_dict=True)
for class_label in report:
if class_label.isdigit(): # クラスが整数である場合
precision = report[class_label]['precision']
recall = report[class_label]['recall']
f1_score = report[class_label]['f1-score']
print(f"クラス {class_label} - 適合率 (Precision): {precision}, 再現率 (Recall): {recall}, F1スコア: {f1_score}")
# 混同行列
print("混同行列:\n", confusion_matrix(y_test, y_pred))
# ROC曲線の計算
fpr, tpr, thresholds = roc_curve(y_test, y_prob)
roc_auc = auc(fpr, tpr) # AUCの計算
# ROC曲線のプロット
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='blue', lw=2, label=f'ROC曲線 (AUC = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='gray', linestyle='--', label='ランダム予測ライン') # ランダム予測線
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('偽陽性率 (False Positive Rate)')
plt.ylabel('真陽性率 (True Positive Rate)')
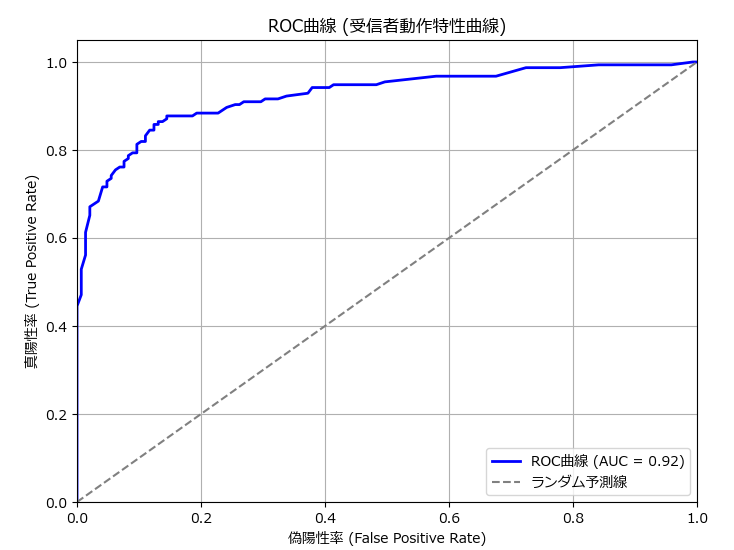
plt.title('ROC曲線 (受信者動作特性曲線)')
plt.legend(loc="lower right")
plt.grid()
plt.show()正確度 (Accuracy): 85.67%
クラス 0 - 適合率 (Precision): 0.8269230769230769, 再現率 (Recall): 0.8896551724137931, F1スコア: 0.8571428571428571
クラス 1 - 適合率 (Precision): 0.8888888888888888, 再現率 (Recall): 0.8258064516129032, F1スコア: 0.8561872909698997
混同行列:
[[129 16]
[ 27 128]]
分類モデルを評価する自作関数
テストデータと予測結果を引数に渡すと、今回紹介した分類精度の評価指数を全て出力する evaluate_classification_metrics()関数と、ROCのグラフを描画するplot_roc_curve() 関数を作りました。
# サンプルデータの作成(バイナリ分類)
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
# データの作成と分割
X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# ランダムフォレストモデルの訓練
model = RandomForestClassifier(n_estimators=100, random_state=42)
model.fit(X_train, y_train)
# 予測
y_pred = model.predict(X_test)
# 陽性クラスの確率を取得(0列目:クラス0の確率、1列目:クラス1の確率が格納されている)
y_prob = model.predict_proba(X_test)[:, 1]
# 精度評価指標の表示
evaluate_classification_metrics(y_test, y_pred)
# ROC曲線の描画
plot_roc_curve(y_test, y_prob)正確度 (Accuracy): 85.67%
クラス 0 - 適合率 (Precision): 0.83, 再現率 (Recall): 0.89, F1スコア: 0.86
クラス 1 - 適合率 (Precision): 0.89, 再現率 (Recall): 0.83, F1スコア: 0.86
混同行列:
[[129 16]
[ 27 128]]
下記は、多値分類のROC曲線のサンプルです。
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
# サンプルデータの生成(4種類に分類可能な100次元のデータを200個生成)
X, y = make_classification(n_samples=200, n_features=100, n_informative=4, n_redundant=0, n_clusters_per_class=1, n_classes=4, random_state=42)
# データを訓練用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# ランダムフォレストの使用
rf = RandomForestClassifier(n_estimators=100, random_state=42)
# モデルの訓練
rf.fit(X_train, y_train)
# テストデータで予測
y_pred_rf = rf.predict(X_test)
y_score_rf = rf.predict_proba(X_test)
plot_roc_curve_multi(y_test, y_score_rf, classes=[0, 1, 2, 3])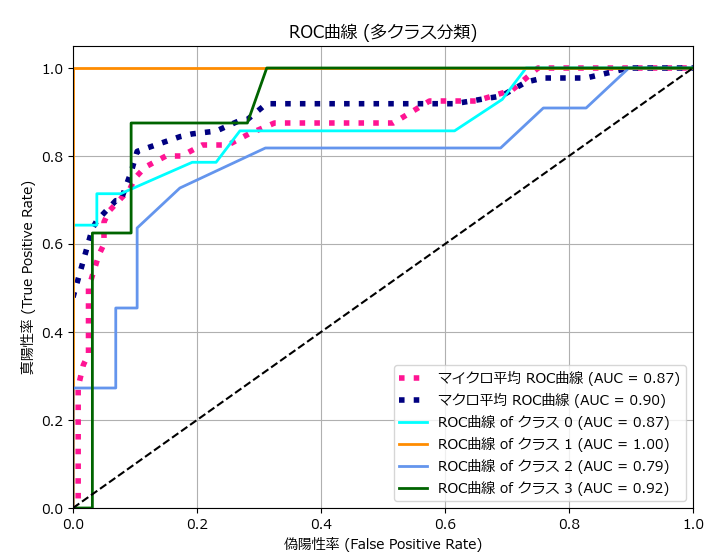
自作関数のソースコード
評価指標出力関数
| 項目 | 詳細 |
|---|---|
| 関数名 | evaluate_classification_metrics(y_true ,y_pred) |
| 概要 | モデルの予測結果に基づいて、精度評価指標(Accuracy、Precision、Recall、F1-score)と混同行列を表示する関数。 |
| パラメータ | - y_true: 実際のクラスラベル(テストデータの正解)。- y_pred: モデルの予測結果(予測されたクラスラベル)。 |
| 戻り値 | 混同行列を返す。 全ての結果は標準出力に表示されるが、混同行列を可視化したい場合、この戻り値を使う。 |
| 詳細 | - 精度(Accuracy): 正しく分類されたインスタンスの割合。 - 適合率(Precision): 正と予測されたインスタンスのうち、実際に正であったものの割合。 - 再現率(Recall): 実際に正であったインスタンスのうち、正しく予測されたものの割合。 - F1スコア: 適合率と再現率の調和平均。 - 混同行列: 各クラスの予測結果を行列形式で表示。 |
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc, accuracy_score, classification_report, confusion_matrix
import numpy as np
import matplotlib
# 日本語フォントの設定
matplotlib.rcParams['font.family'] = 'Meiryo'
# 各クラスごとの精度評価指標(Precision, Recall, F1-score)と混同行列を出力する関数
def evaluate_classification_metrics(y_true, y_pred):
"""
モデルの予測結果に基づいて、精度評価指標(Accuracy、Precision、Recall、F1-score)と
混同行列を表示する関数。
Parameters:
y_true (array-like): 実際のクラスラベル(テストデータの正解)
y_pred (array-like): モデルの予測結果(予測されたクラスラベル)
Returns:
None: 結果は標準出力に表示される
"""
# 精度の計算(Accuracy)
accuracy = accuracy_score(y_true, y_pred)
print(f"正確度 (Accuracy): {accuracy * 100:.2f}%") # 精度をパーセンテージで表示
# クラスごとのPrecision、Recall、F1-scoreを計算し、表示
report = classification_report(y_true, y_pred, output_dict=True)
for class_label in report:
if class_label.isdigit(): # クラスラベルが整数である場合のみ処理
precision = report[class_label]['precision']
recall = report[class_label]['recall']
f1 = report[class_label]['f1-score']
print(f"クラス {class_label} - 適合率 (Precision): {precision:.2f}, 再現率 (Recall): {recall:.2f}, F1スコア: {f1:.2f}")
# 混同行列の表示
cm = confusion_matrix(y_true, y_pred)
print("混同行列:")
print(cm)
return cmROC描画関数(2値分類用)
| 項目 | 詳細 |
|---|---|
| 関数名 | plot_roc_curve(y_true ,y_prob ,filename = None) |
| 概要 | ROC曲線を描画し、AUC(Area Under Curve)を表示する関数。 |
| パラメータ | - y_true: 実際のクラスラベル(テストデータの正解)。- y_prob: モデルの予測確率(陽性クラスの予測確率)。- filename: グラフを保存するファイル名。 |
| 戻り値 | なし。ROC曲線がプロットされ、グラフが表示される。 |
| 詳細 | - ROC曲線 (Receiver Operating Characteristic curve): モデルの真陽性率(TPR)と偽陽性率(FPR)の関係を視覚化した曲線。 - AUC (Area Under Curve): ROC曲線の下の面積を計算し、モデルの性能を定量的に評価する指標。 1に近いほど良いモデルとされる。 - ランダム予測線: 真陽性率と偽陽性率が同じ場合(ランダムな予測)を示す直線(y = x)を描画。 |
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc
import numpy as np
import matplotlib
# 日本語フォントの設定
matplotlib.rcParams['font.family'] = 'Meiryo'
# ROC曲線を描画してファイルに保存する関数
def plot_roc_curve(y_true, y_prob, filename=None, pos_label=1):
"""
ROC曲線を描画し、AUC(Area Under Curve)を表示する関数。
引数にファイル名を指定した場合、グラフをそのファイルに保存します。
Parameters:
y_true (array-like): 実際のクラスラベル(テストデータの正解)
y_prob (array-like): モデルの予測確率(陽性クラスの予測確率)
filename (str, optional): 保存するファイルのパス。指定しない場合、グラフは表示されるのみです。
pos_label (int): 陽性(ポジティブ)クラスとして扱いたいラベル(初期値は1)
Returns:
None: グラフは表示またはファイルに保存される
"""
# ROC曲線を計算
fpr, tpr, thresholds = roc_curve(y_true, y_prob, pos_label=pos_label)
roc_auc = auc(fpr, tpr) # AUCの計算
# ROC曲線をプロット
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='blue', lw=2, label=f'ROC曲線 (AUC = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='gray', linestyle='--', label='ランダム予測線') # ランダム予測線(y = xの線)
plt.xlim([0.0, 1.0]) # x軸の範囲(偽陽性率)
plt.ylim([0.0, 1.05]) # y軸の範囲(真陽性率)
plt.xlabel('偽陽性率 (False Positive Rate)') # x軸ラベル
plt.ylabel('真陽性率 (True Positive Rate)') # y軸ラベル
plt.title('ROC曲線 (受信者動作特性曲線)') # グラフタイトル
plt.legend(loc="lower right") # 凡例
plt.grid() # グリッド表示
# ファイル名が指定されている場合は保存、それ以外は表示
if filename:
plt.savefig(filename)
print(f"ROC曲線が '{filename}' に保存されました。")
else:
plt.show() # グラフを表示ROC描画関数(多値分類用)
| 項目 | 詳細 |
|---|---|
| 関数名 | plot_roc_curve_multi(y_true, y_prob, classes, filename = None) |
| 概要 | ROC曲線を描画し、AUC(Area Under Curve)を表示する関数。 |
| パラメータ | - y_true: 実際のクラスラベル(テストデータの正解)。- y_score: モデルの予測確率(陽性クラスの予測確率)。- classes: 分類クラスのリスト。- filename: グラフを保存するファイル名。 |
| 戻り値 | なし。ROC曲線がプロットされ、グラフが表示される。 |
| 詳細 | - ROC曲線 (Receiver Operating Characteristic curve): モデルの真陽性率(TPR)と偽陽性率(FPR)の関係を視覚化した曲線。 - AUC (Area Under Curve): ROC曲線の下の面積を計算し、モデルの性能を定量的に評価する指標。 1に近いほど良いモデルとされる。 - ランダム予測線: 真陽性率と偽陽性率が同じ場合(ランダムな予測)を示す直線(y = x)を描画。 |
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc
import numpy as np
import matplotlib
# 日本語フォントの設定
matplotlib.rcParams['font.family'] = 'Meiryo'
from sklearn.preprocessing import label_binarize
# ROC曲線(多値)をプロットする関数
def plot_roc_curve_multi(y_true, y_score, classes, filename=None):
"""
多クラス分類のROC曲線をプロットする関数。
Parameters:
y_true (array-like): 実際のクラスラベル(テストデータの正解)
y_score (array-like): モデルの予測確率
classes (list): 分類クラスのリスト
filename (str, optional): 保存するファイルのパス。指定しない場合、グラフは表示されるのみ
Returns:
None: グラフは表示またはファイルに保存される
"""
# ラベルをバイナリ形式に変換
y_true_bin = label_binarize(y_true, classes=classes)
n_classes = y_true_bin.shape[1]
# ROC曲線の計算
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
fpr[i], tpr[i], _ = roc_curve(y_true_bin[:, i], y_score[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])
# マイクロ平均とマクロ平均のROC曲線を計算
fpr["micro"], tpr["micro"], _ = roc_curve(y_true_bin.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])
# マクロ平均のROC曲線を計算
all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)]))
mean_tpr = np.zeros_like(all_fpr)
for i in range(n_classes):
mean_tpr += np.interp(all_fpr, fpr[i], tpr[i])
mean_tpr /= n_classes
fpr["macro"] = all_fpr
tpr["macro"] = mean_tpr
roc_auc["macro"] = auc(fpr["macro"], tpr["macro"])
# ROC曲線をプロット
plt.figure(figsize=(8, 6))
plt.plot(fpr["micro"], tpr["micro"], color='deeppink', linestyle=':', linewidth=4, label=f'マイクロ平均 ROC曲線 (AUC = {roc_auc["micro"]:.2f})')
plt.plot(fpr["macro"], tpr["macro"], color='navy', linestyle=':', linewidth=4, label=f'マクロ平均 ROC曲線 (AUC = {roc_auc["macro"]:.2f})')
colors = ['aqua', 'darkorange', 'cornflowerblue', 'darkgreen']
for i, color in zip(range(n_classes), colors):
plt.plot(fpr[i], tpr[i], color=color, lw=2, label=f'ROC曲線 of クラス {i} (AUC = {roc_auc[i]:.2f})')
plt.plot([0, 1], [0, 1], 'k--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('偽陽性率 (False Positive Rate)')
plt.ylabel('真陽性率 (True Positive Rate)')
plt.title('ROC曲線 (多クラス分類)')
plt.legend(loc="lower right")
plt.grid()
if filename:
plt.savefig(filename)
print(f"ROC曲線が '{filename}' に保存されました。")
else:
plt.show()まとめ
本記事では、機械学習の分類予測精度の評価指標の概要と、Precision, Recall, Accuracy, F1, ROCついて、具体的なサンプルコード付きで解説しました。
Accuracyは直感的に理解しやすい指標ですが、クラス不均衡がある場合に不適切な結果を導くことがあります。そのため、PrecisionやRecallを使い分ける必要があります。
本記事の内容が、機械学習の分類問題におけるモデル評価方法の理解に少しでもお役に立てば幸いです









コメント