回帰モデルの性能を評価する指標はいくつかあり、どの指標を選ぶかでモデルの「良さ」が大きく変わります。
例えば、予測値と実測値のズレを直感的に把握できる Mean Absolute Error (MAE) や、大きな誤差を強調する Mean Squared Error (MSE) や Root Mean Squared Error (RMSE)、また、モデル全体の精度を示す 決定係数 (R²) などがよく使われます。
さらに、これらの評価指標だけでは表しきれない情報を補完するために、残差プロットや実測値と予測値のプロット、誤差分布を示すヒストグラムなどのグラフが非常に有効です。
本記事では、これらの評価指標について分かりやすく解説するとともに、視覚的に結果を理解するためのグラフ作成方法も紹介します。また、評価指標とグラフを簡単に出力できる自作関数も提供しており、実践ですぐに活用できます。興味のある方は、是非ご一読ください。
回帰モデルにおける評価指標の概要
回帰モデルの評価指標は、モデルがどれだけ正確に連続値を予測できるかを測定するための基準です。モデルの性能を客観的に比較・評価し、最適なモデルを選択するために使用されます。
回帰タスクでは、予測値と実測値の差を基にさまざまな指標が計算されます。以下に、代表的な評価指標を一覧で示します。
| 指標 | 意味 | 特徴 | 適用例 |
|---|---|---|---|
| MAE | 平均絶対誤差 | 誤差の平均を絶対値で計算するため、直感的に解釈しやすい。 誤差の大きさを定量的に把握可能。 | 設備の予知保全、コスト予測 |
| MSE | 平均二乗誤差 | 誤差を二乗するため、大きな誤差をより強調。大きな誤差の影響を把握可能。 | エネルギー消費量の予測、精密計測 |
| RMSE | 二乗平均平方根誤差 | MSEの平方根をとることで、単位が元のデータと同じになる。 | 需要予測、温度変動の予測 |
| MAPE | 平均絶対パーセント誤差 | 誤差を実測値で割り、割合として示すため、スケールに依存しない。 | 売上予測、原料使用量の予測 |
| R²(決定係数) | データのばらつきをどれだけ説明できるかを示す | 値が1に近いほど性能が良い。全体的な予測精度を簡潔に把握可能。 | 製造ラインの性能分析、需要予測 |
これらの指標はモデルの目的やデータの特性に応じて使い分ける必要があります。
評価指標の説明
平均絶対誤差 (Mean Absolute Error, MAE)
平均絶対誤差 (MAE) は、予測値と実測値のズレの絶対値の平均を表します。値が小さいほどモデルの予測精度が高いことを示します。直感的に解釈しやすく、特に誤差が極端に大きくない場合に適した指標です。
MAEはスケール依存型の指標であり、データの単位を考慮する必要があります。また、誤差の絶対値を使用するため、大きな誤差を特に強調する必要がない場面で有用です。
このコードを実行すると、モデルの平均的な誤差が直感的な数値として得られます。
from sklearn.metrics import mean_absolute_error
# MAEの計算(y_true:実測データ, y_pred:予測データ)
mae = mean_absolute_error(y_true, y_pred)
print(f"Mean Absolute Error (MAE): {mae:.2f}")平均二乗誤差 (Mean Squared Error, MSE)
平均二乗誤差 (MSE) は、予測値と実測値のズレを二乗した値の平均を表します。誤差を二乗することで、大きな誤差を強調する特徴があります。値が小さいほどモデルの性能が良いとされます。
MSEは大きな誤差を許容しないタスクに向いていますが、単位が二乗されるため、結果を解釈する際に注意が必要です。
from sklearn.metrics import mean_squared_error
# MSEの計算(y_true:実測データ, y_pred:予測データ)
mse = mean_squared_error(y_true, y_pred)
print(f"Mean Squared Error (MSE): {mse:.2f}")二乗平均平方根誤差 (Root Mean Squared Error, RMSE)
二乗平均平方根誤差 (RMSE) は、MSEの平方根をとった指標で、誤差の単位が元データと一致するため、結果を解釈しやすくなります。大きな誤差を強調しつつ、直感的な理解が可能です。
この指標は、モデルがどの程度正確に予測できているかを、より実用的な形で示します。
import numpy as np
from sklearn.metrics import mean_squared_error
# RMSEの計算(y_true:実測データ, y_pred:予測データ)
rmse = np.sqrt(mean_squared_error(y_true, y_pred))
print(f"Root Mean Squared Error (RMSE): {rmse:.2f}")
平均絶対パーセント誤差 (Mean Absolute Percentage Error, MAPE)
平均絶対パーセント誤差 (MAPE) は、予測値と実測値の誤差を実測値で割った割合の平均を表します。スケールに依存しないため、データの単位が異なる場合でも比較可能です。
但し、実際の値がゼロまたはゼロに近い場合、MAPEの値が非常に大きくなり、評価が難しくなることがあります。
下記は、多値分類にも対応したPrecisionとRecallの出力サンプルです。
import numpy as np
# MAPEの計算(y_true:実測データ, y_pred:予測データ)
mape = np.mean(np.abs((y_true - y_pred) / y_true)) * 100
print(f"Mean Absolute Percentage Error (MAPE): {mape:.2f}%")決定係数 (R², Coefficient of Determination)
決定係数 (R²) は、モデルがデータのばらつきをどの程度説明できているかを示す指標です。値は0~1の範囲で、1に近いほど性能が高いことを意味します。
from sklearn.metrics import r2_score
# R²の計算(y_true:実測データ, y_pred:予測データ)
r2 = r2_score(y_true, y_pred)
print(f"Coefficient of Determination (R²): {r2:.2f}")評価指標を視覚化するためのグラフ
回帰モデルを評価する際に、数値だけでなく、結果を視覚的に確認することも重要です。視覚化することで、モデルの精度や予測の傾向、誤差の分布を直感的に理解しやすくなります。今回は、回帰モデルの評価においてよく使用される視覚化グラフをいくつか紹介します。
| グラフの種類 | 特徴 | 使用目的 |
|---|---|---|
| 残差プロット | 予測誤差(残差)をプロット | モデルの精度や誤差の分布を評価する |
| 実測値 vs 予測値プロット | 実際の値と予測値を比較するプロット | 予測の精度を直感的に評価する |
| 誤差分布ヒストグラム | 予測誤差の分布を示すヒストグラム | モデルの誤差の傾向を評価する |
| QQプロット | 残差が正規分布に従っているかを確認するプロット | 残差の正規性を評価し、モデルの前提条件を確認する |
| 学習曲線 | モデルのトレーニングデータに対するパフォーマンスの推移をプロット | モデルの学習の進行状況と過学習・未学習を評価する |
この章で紹介するグラフのソースコードは、下記ソースコードの末尾に追加することで実行可能です。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression
# データの作成
X, y = make_regression(n_samples=100, n_features=1, noise=10)
# モデルの学習
model = LinearRegression()
model.fit(X, y)
# 予測
y_pred = model.predict(X)
# 残差の計算
residuals = y - y_pred
# ★★★ 以下にグラフ描画のソースコードを追加して実行してください ★★★残差プロット(Residual Plot)
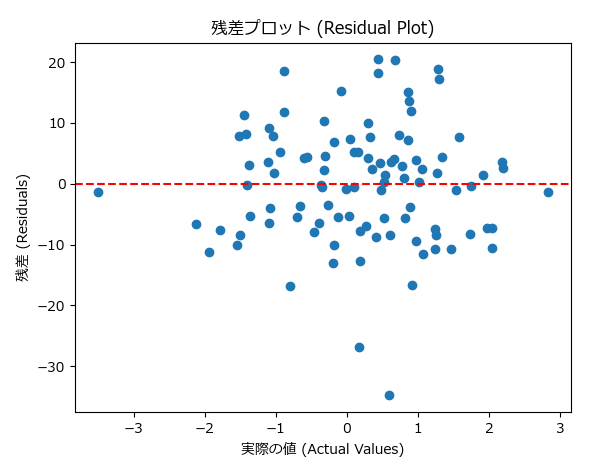
残差プロットは、モデルの予測誤差(残差)をプロットするグラフです。残差とは、予測値と実際の値との差を指します。このプロットを使うことで、モデルがどの範囲でうまく予測していないか、また誤差の傾向があるかどうかを確認できます。
- 特徴:残差がランダムに分布しているとき、モデルは良好に機能していると言えます。
- 問題の兆候:残差にパターンが見られる場合(例えば、トレンドがある場合)、モデルは適切に学習できていない可能性があります。
# 残差プロットの描画
plt.scatter(X, residuals)
plt.axhline(y=0, color='r', linestyle='--') # y=0の水平線
plt.xlabel('実際の値 (Actual Values)')
plt.ylabel('残差 (Residuals)')
plt.title('残差プロット (Residual Plot)')
plt.show()実測値 vs 予測値プロット(Actual vs Predicted Plot)
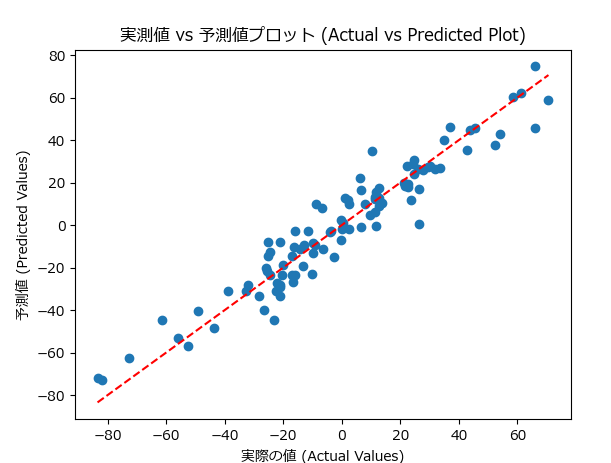
実測値 vs 予測値プロットは、モデルの予測結果と実際の値を比較するグラフです。理想的には、すべての予測値が実際の値と一致する点(直線)上に並ぶことが望まれます。このプロットは、モデルがどれだけ正確に予測できているかを視覚的に評価するために有効です。
- 特徴:予測値が実際の値と一致するほど、グラフは直線に近づきます。
- 問題の兆候:予測が実際の値からずれている場合、モデルの精度が低いことを示します。
# 実測値と予測値のプロット
plt.scatter(y, y_pred)
plt.plot([min(y), max(y)], [min(y), max(y)], color='red', linestyle='--') # 理想的な予測線
plt.xlabel('実際の値 (Actual Values)')
plt.ylabel('予測値 (Predicted Values)')
plt.title('実測値 vs 予測値プロット (Actual vs Predicted Plot)')
plt.show()誤差分布ヒストグラム(Error Distribution Histogram)
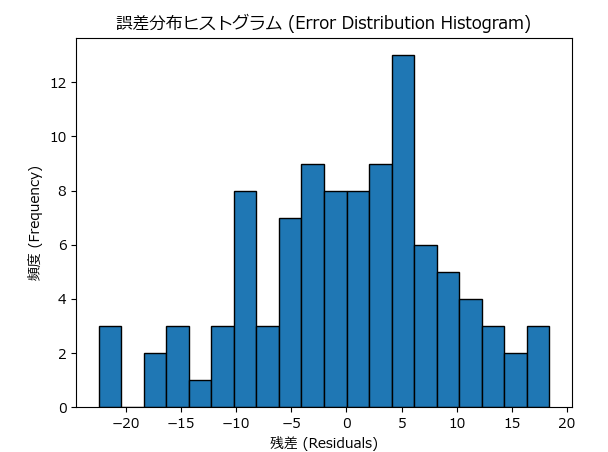
誤差分布ヒストグラムは、モデルの予測誤差(残差)の分布を示すグラフです。このヒストグラムを使って、誤差がどのように分布しているか(例えば、正規分布しているか)を確認できます。理想的には、誤差が均等に分布し、中心に集まっていることが望まれます。
- 特徴:誤差が正規分布していれば、モデルは一般的に良好な予測をしていると言えます。
- 問題の兆候:誤差が偏っていたり、異常値が多い場合、モデルの学習に問題がある可能性があります。
# 誤差分布のヒストグラム
plt.hist(residuals, bins=20, edgecolor='black')
plt.xlabel('残差 (Residuals)')
plt.ylabel('頻度 (Frequency)')
plt.title('誤差分布ヒストグラム (Error Distribution Histogram)')
plt.show()QQプロット(Quantile-Quantile Plot)
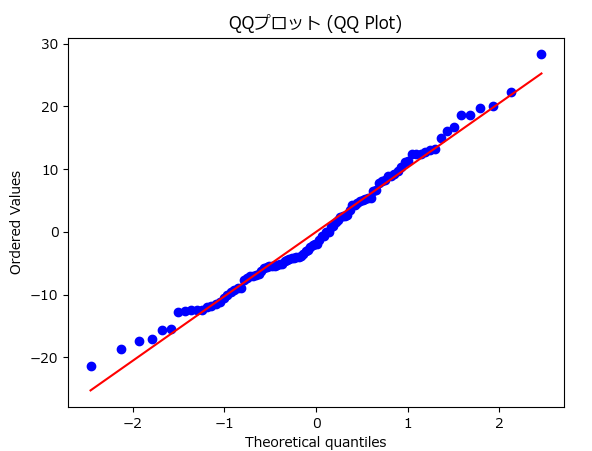
QQプロットは、データが特定の理論的分布(通常は正規分布)に従っているかどうかを視覚的に確認するためのグラフです。回帰モデルでは、残差が正規分布に従うことが前提とされる場合が多いため、QQプロットは非常に有用です。
- 正規分布に従う場合:プロット上の点は直線に沿った形になるはずです。
- 正規分布に従わない場合:残差に偏りがあることが視覚的に示され、モデルの改善が必要であることが分かります。
import scipy.stats as stats
# QQプロット
stats.probplot(residuals, dist="norm", plot=plt)
plt.title('QQプロット (QQ Plot)')
plt.show()学習曲線(Learning Curve)
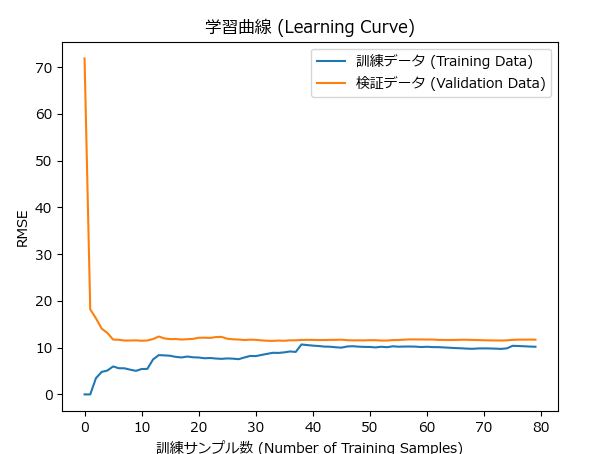
学習曲線は、モデルのトレーニングデータに対するパフォーマンス(例えば、損失関数や精度)がトレーニングデータのサイズに対してどのように変化するかを示すグラフです。学習曲線を描くことで、以下の情報を得ることができます。
- モデルが学習しているかどうか:トレーニングデータが増えることで精度が向上するならば、モデルは正しく学習していると言えます。
- 過学習と未学習の兆候:トレーニングデータに対しては精度が良いのに、テストデータに対しては精度が低い場合は過学習の兆候です。
学習曲線を使用することで、モデルの学習プロセスを可視化し、どの段階で学習が止まっているか、またはどの程度まで学習が進んでいるかを確認できます。
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# データの分割
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)
train_errors, val_errors = [], []
# トレーニングの反復
for m in range(1, len(X_train) + 1):
model.fit(X_train[:m], y_train[:m])
y_train_predict = model.predict(X_train[:m])
y_val_predict = model.predict(X_val)
train_errors.append(mean_squared_error(y_train[:m], y_train_predict))
val_errors.append(mean_squared_error(y_val, y_val_predict))
# 学習曲線の描画
plt.plot(np.sqrt(train_errors), label="訓練データ (Training Data)")
plt.plot(np.sqrt(val_errors), label="検証データ (Validation Data)")
plt.xlabel('訓練サンプル数 (Number of Training Samples)')
plt.ylabel('RMSE')
plt.title('学習曲線 (Learning Curve)')
plt.legend()
plt.show()評価指標の具体例
下記のプログラムはランダムフォレストを使って精度指標を求めたサンプルです。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_regression
from sklearn.ensemble import RandomForestRegressor
import matplotlib
# 日本語フォントの設定
matplotlib.rcParams['font.family'] = 'Meiryo' # メイリオを指定
# サンプルデータの作成(回帰)
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=42)
# データをトレーニングセットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# ランダムフォレストモデルの訓練
model = RandomForestRegressor(n_estimators=100, random_state=42)
model.fit(X_train, y_train)
# 予測
y_pred = model.predict(X_test)
# 評価指標の計算
mae = mean_absolute_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
r2 = r2_score(y_test, y_pred)
# 評価指標の出力
print(f"平均絶対誤差 (MAE): {mae:.2f}")
print(f"平均二乗誤差 (MSE): {mse:.2f}")
print(f"二乗平均平方根誤差 (RMSE): {rmse:.2f}")
print(f"決定係数 (R²): {r2:.2f}")
# 実測値と予測値のプロット
plt.figure(figsize=(8, 6))
plt.scatter(y_test, y_pred, alpha=0.5, color='blue', label='予測値')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], color='red', linestyle='--', label='完全予測ライン')
plt.xlabel('実測値')
plt.ylabel('予測値')
plt.title('実測値と予測値の比較')
plt.legend()
plt.grid()
plt.show()平均絶対誤差 (MAE): 68.47
平均二乗誤差 (MSE): 7408.62
二乗平均平方根誤差 (RMSE): 86.07
決定係数 (R²): 0.81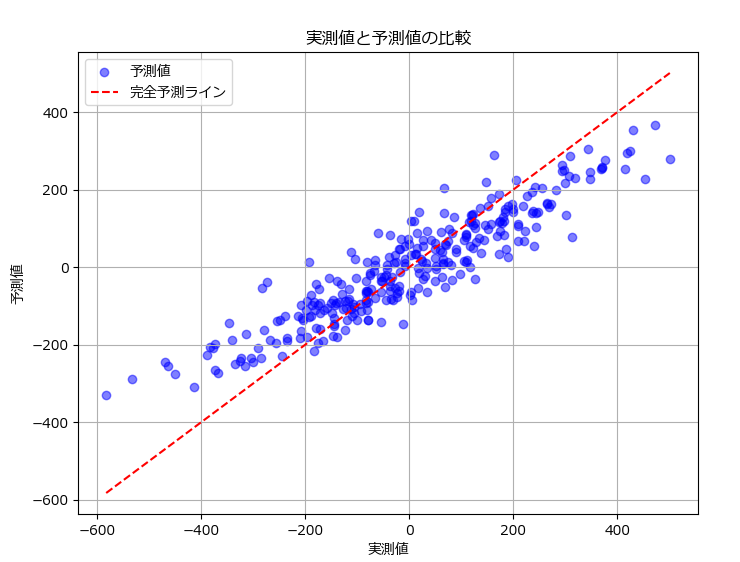
分類モデルを評価する自作関数
テストデータと予測結果を引数に渡すと、今回紹介した分類精度の評価指数を全て出力する evaluate_regression_metrics()関数と、ROCのグラフを描画するplot_regression_graphs() 関数を作りました。
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
from sklearn.datasets import make_regression
# サンプルデータの作成(回帰)
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=42)
# データを訓練用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# ランダムフォレスト回帰モデルの訓練
model = RandomForestRegressor(n_estimators=100, random_state=42)
model.fit(X_train, y_train)
# 予測
y_pred = model.predict(X_test)
# 回帰モデルの評価指標を表示
evaluate_regression_metrics(y_test, y_pred)
# 回帰モデルのグラフを表示または保存
# 画面に表示する場合
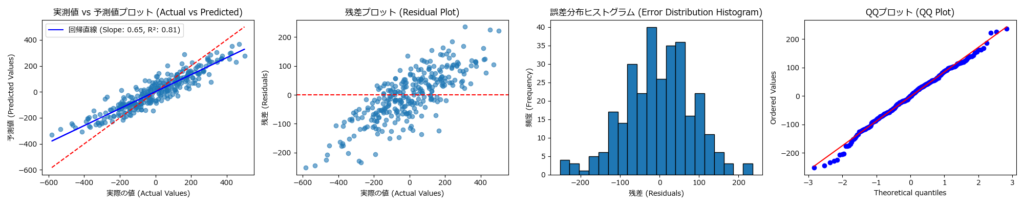
plot_regression_graphs(y_test, y_pred)
# ファイルに保存する場合
# plot_regression_graphs(y_test, y_pred, filename='regression_analysis_results.png')平均絶対誤差 (MAE): 68.47
平均二乗誤差 (MSE): 7408.62
二乗平均平方根誤差 (RMSE): 86.07
決定係数 (R²): 0.81
ソースコードとリファレンス
評価指標出力関数
| 項目 | 詳細 |
|---|---|
| 関数名 | evaluate_regression_metrics(y_true, y_pred) |
| 概要 | 回帰モデルの評価指標(MAE、MSE、RMSE、R²)を計算して表示する関数。 |
| パラメータ | - y_true: 実際の値の配列実際の値を含む配列(またはリスト)。 長さは y_pred と同じでなければならない。- y_pred: 予測値の配列モデルが予測した値を含む配列(またはリスト)。 長さは y_true と同じでなければならない。 |
| 戻り値 | なし。 関数は評価指標を標準出力(コンソール)に表示します。 |
import numpy as np
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
# 評価指標を表示する関数
def evaluate_regression_metrics(y_true, y_pred):
"""
回帰モデルの評価指標(MAE、MSE、RMSE、R²)を計算して表示する関数。
"""
# 各指標の計算
mae = mean_absolute_error(y_true, y_pred)
mse = mean_squared_error(y_true, y_pred)
rmse = np.sqrt(mse)
r2 = r2_score(y_true, y_pred)
# 各指標を表示
print(f"平均絶対誤差 (MAE): {mae:.2f}")
print(f"平均二乗誤差 (MSE): {mse:.2f}")
print(f"二乗平均平方根誤差 (RMSE): {rmse:.2f}")
print(f"決定係数 (R²): {r2:.2f}")グラフ表示関数
| 項目 | 詳細 |
|---|---|
| 関数名 | plot_regression_graphs(y_true,y_pred,filename=None, |
| 概要 | 実測値と予測値、残差プロット、誤差分布、QQプロットを表示する関数。グラフは指定されたファイル名で保存することもできます。 |
| パラメータ | - y_true: 実際の値の配列- y_pred: 予測値の配列- filename: 保存するファイル名。初期値は None- nrows: グラフのサブプロットの行数。初期値は 1- ncols: グラフのサブプロットの列数。初期値は 4 |
| 戻り値 | なし。 グラフを表示するか、指定されたファイル名で保存します。 |
| 詳細 | nrows=2,ncols=2 にすると、縦2列、横2列でグラフを描画します。 グラフを縦に並べたい場合は、nrows=4,ncols=1 にしてください。 |
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
from sklearn.metrics import r2_score
import matplotlib
# 日本語フォントの設定
matplotlib.rcParams['font.family'] = 'Meiryo' # メイリオを指定
# グラフを表示または保存する関数
def plot_regression_graphs(y_true, y_pred, filename=None, nrows=1, ncols=4):
"""
実測値と予測値、残差、誤差分布、QQプロットを表示する関数。
- `filename` が指定されていれば、グラフをそのファイル名で保存。
- `nrows` と `ncols` はグラフの行数と列数。
"""
# サブプロットの設定
fig, axs = plt.subplots(nrows, ncols, figsize=(5 * ncols, 4 * nrows))
# axsが2次元配列か確認
axs = axs.flatten() # 1次元配列にフラット化
# 実測値 vs 予測値プロット
axs[0].scatter(y_true, y_pred, alpha=0.6)
axs[0].plot([min(y_true), max(y_true)], [min(y_true), max(y_true)], color='red', linestyle='--') # 理想的な予測線
axs[0].set_xlabel('実際の値 (Actual Values)')
axs[0].set_ylabel('予測値 (Predicted Values)')
axs[0].set_title('実測値 vs 予測値プロット (Actual vs Predicted)')
# 回帰直線の計算と表示
slope, intercept = np.polyfit(y_true, y_pred, 1)
r2 = r2_score(y_true, y_pred)
axs[0].plot(y_true, slope * y_true + intercept, color='blue', linestyle='-', label=f'回帰直線 (Slope: {slope:.2f}, R²: {r2:.2f})')
axs[0].legend()
# 残差プロット
residuals = y_true - y_pred
axs[1].scatter(y_true, residuals, alpha=0.6)
axs[1].axhline(y=0, color='r', linestyle='--') # y=0の水平線
axs[1].set_xlabel('実際の値 (Actual Values)')
axs[1].set_ylabel('残差 (Residuals)')
axs[1].set_title('残差プロット (Residual Plot)')
# 誤差分布ヒストグラム
axs[2].hist(residuals, bins=20, edgecolor='black')
axs[2].set_xlabel('残差 (Residuals)')
axs[2].set_ylabel('頻度 (Frequency)')
axs[2].set_title('誤差分布ヒストグラム (Error Distribution Histogram)')
# QQプロット
stats.probplot(residuals, dist="norm", plot=axs[3])
axs[3].set_title('QQプロット (QQ Plot)')
plt.tight_layout()
# ファイル名が指定されていれば、グラフを保存
if filename:
plt.savefig(filename)
print(f"グラフを '{filename}' として保存しました。")
else:
plt.show()まとめ
本記事では、機械学習における回帰モデルの評価指標(MAE、MSE、RMSE、MAPE、R²)について、サンプルプログラムを交えて解説しました。
また、評価指標の補助として使われるグラフ(残差プロット、実測値 vs 予測値プロット、誤差分布ヒストグラム、QQプロット)についてもサンプルプログラムと実際の出力結果を合わせて紹介しました。
最後に、今回紹介した評価指標の計算と、グラフによる可視化が簡単に行える自作関数について、その使い方とソースコードを公開しました。
これらの評価指標とグラフを活用すれば、回帰モデルの性能をより深く理解し、改善のためのヒントを得ることができるでしょう。本記事がみなさんのお役に立てれば幸いです。









コメント