機械学習のアルゴリズムは数多くありますが、「より高い精度を実現し、複雑なデータにも柔軟に対応したい!」そんなときに頼れるのが 勾配ブースティング決定木(Gradient Boosting Decision Trees, GBDT) です。
GBDTは、決定木を組み合わせてモデルの性能を向上させるアルゴリズムですが、ランダムフォレストとは異なり、各木が前の木の誤差を学習することで精度を高めていく 逐次学習 のアプローチを採用しています。また、過学習を抑えるための正則化が組み込まれている点も大きな特徴です。
本記事では、GBDTを活用して分類問題と回帰問題を解く方法を、サンプルコード付きでわかりやすく解説します。
Pythonでの実装方法はもちろん、ランダムフォレストとの違いや、メリット・デメリット、パラメータチューニングのポイントまで幅広く網羅していますので、GBDTを使ってモデルを改善したいという方は、ぜひご一読ください。
GDBTとは
GDBT(Gradient Boosting Decision Tree)は、機械学習における勾配ブースティングというアンサンブル学習の一種で、回帰や分類といった幅広い問題に対応できます。GDBTは複数の決定木を直列につなげて学習を進めることで、誤差を段階的に修正し、より精度の高い予測モデルを構築するのが特徴です。
ノイズに強く、非線形な関係も学習可能で、データサイエンス実務やKaggleコンペでも広く使用されています。

GDBTの仕組み

GDBTは以下のように構築されます
- 残差の計算:
初期モデルを作り、各データに対して予測誤差(残差)を計算します。 - 弱学習器(小さな決定木)を学習:
残差を予測する小さな決定木を作成し、元のモデルに追加していきます。 - モデルの更新:
新しい木の予測を加えることで、全体モデルが改善されます。この処理を繰り返すことで誤差を少しずつ減らしていきます。
このように、GDBTは前のモデルの誤りを補正するように新しい木を追加していく「ブースティング」の代表的手法です。
決定木・ランダムフォレストとの違い
| 特徴 | 決定木 | ランダムフォレスト | GDBT |
|---|---|---|---|
| 構造 | 1本の木 | 複数の木(並列) | 複数の木(直列) |
| 過学習のしやすさ | 高い | 低い | やや高い(パラメータ調整が必要) |
| 学習速度 | 速い | 遅い | 遅め |
| 精度 | 単純なデータで高い | 複雑なデータで高い | 非常に高い(チューニング前提) |
| 特徴量選択 | 全特徴量 | ランダムに一部選択 | 全特徴量(重要度に基づく分割) |
GDBTのメリット・デメリット
メリット
- 高精度な予測:多くのケースで最も精度の高いアルゴリズムの一つ
- 非線形な関係にも対応:複雑な特徴間の関係を捉えられる
- 特徴量重要度が分かる:どの特徴がどれだけ貢献しているか可視化可能
- 柔軟なカスタマイズ性:損失関数・木の深さ・学習率など細かく制御できる
デメリット
- 学習コストが高い:木を1本ずつ順番に構築するため時間がかかる
- ハイパーパラメータ調整が重要:学習率や木の深さなどの調整が必要
- ノイズに過敏:過学習を起こしやすい(特に小さなデータセット)
- リアルタイム用途にはやや不向き:推論速度もランダムフォレストより遅め
GDBTに適したデータ
向いているデータ
- 特徴量が多く、複雑なパターンを持つデータ
- 高精度な予測が求められる業務(金融、医療、製造業など)
- 適度な量の構造化データ(数値、カテゴリデータなど)
- 回帰・分類どちらにも対応したいタスク
向いていないデータ
- リアルタイム予測が必要なシステム(学習・推論速度がネック)
- 非常に高次元・スパースなデータ(例:生のテキスト)
- ノイズの多いデータ(過学習しやすいため注意が必要)
製造業におけるGDBTの活用例
製造業において、GDBTは次の用途で使われています。
| 用途 | 概要 | タイプ | 具体例 |
|---|---|---|---|
| 異常検知 | センサーデータから異常パターンを検出し、予防保全や品質向上に貢献 | 分類 | 振動・温度・電流などの変動パターンから異常兆候を自動検出 |
| 故障予測 | 機械の状態を学習し、故障の予兆を捉える | 分類 | 異常振動の継続時間や加速度傾向をもとに、ベアリングの故障を予測 |
| 品質予測 | 製造条件と品質データを関連づけ、不良品の発生を抑制 | 回帰 | 温度・圧力・回転数から製品の寸法ばらつきを予測 |
| 需要予測 | 時系列データに基づき、将来の需要や在庫変動を予測 | 回帰 | 生産計画や仕入れ戦略の最適化 |
| 故障分類 | 故障が発生した際、その原因(電気系/機械系など)を分類 | 分類 | ログデータやセンサー値から、適切な対応部門を特定 |
| 生産量最適化 | プロセス条件を調整し、最大効率の生産体制を実現 | 回帰 | 材料投入量・加工時間・気温などから最適な生産条件を推定 |
| エネルギー消費予測 | 設備や工場全体の電力使用量を予測し、省エネ施策やコスト削減に貢献 | 回帰 | 月別・時間帯別の使用傾向からピーク電力を予測し契約電力を最適化 |
GDBT(勾配ブースティング決定木)による分類問題の解き方
1. 事前準備(ライブラリ導入とデータ準備)
まず、以下のライブラリをインストールしてください。
pip install matplotlib
pip install pandas
pip install scikit-learn次に、GDBTの分類モデルを試すためのダミーデータを作成します。今回は、7つの特徴量から4クラスを分類するデータを使用します。製造業での応用としては、センサーによる異常検知や製品の不良予測などに置き換えることができます。
from sklearn.datasets import make_classification
import pandas as pd
# ダミーデータ作成
X, y = make_classification(
n_samples=1000,
n_features=7,
n_informative=5,
n_redundant=2,
n_classes=4,
n_clusters_per_class=1,
flip_y=0.05,
random_state=42
)
# データフレーム化
df = pd.DataFrame(X, columns=[f"特徴量_{i+1}" for i in range(7)])
df['正解データ'] = y
# ファイルに保存(任意)
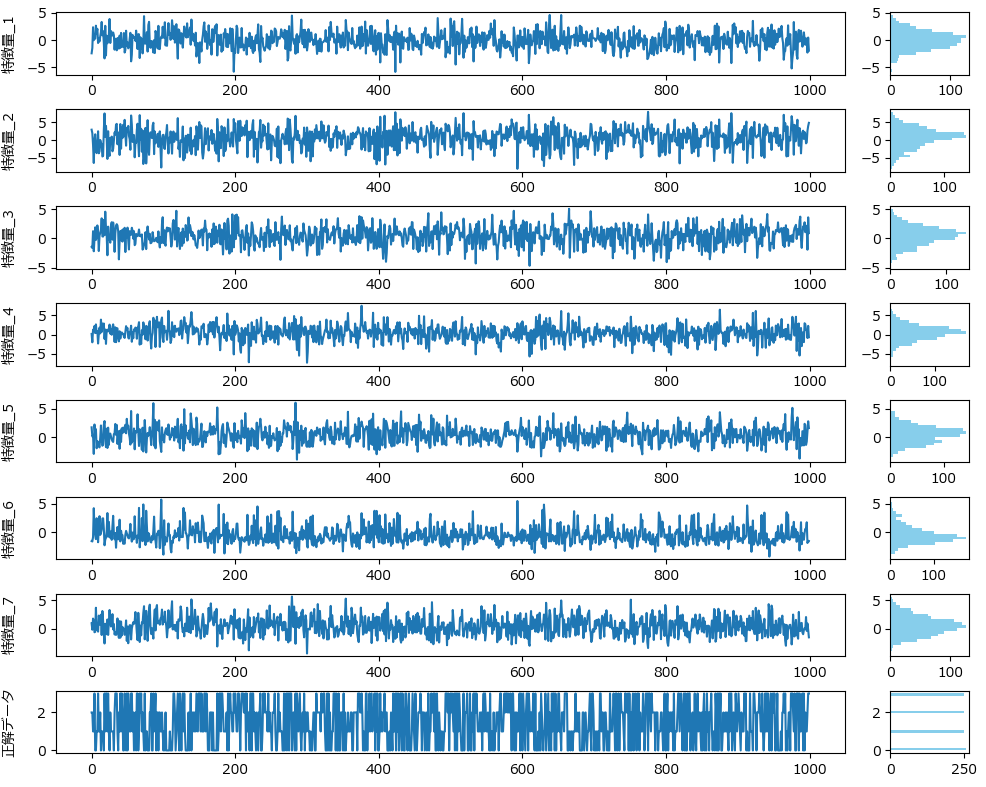
df.to_csv("classification_data.csv", index=False)特徴量_1~7 は一見無秩序に見えるかもしれませんが、GDBTを用いることで目的変数(分類先)を高精度に予測できます。
GDBTを用いた分類モデルの学習と評価(サンプルコードと解説)
以下は、GDBTを用いて分類モデルの学習と評価を行うサンプルコードです。
このまま実行すると学習が始まり、精度評価指標(混同行列、accuracyなど)が出力されます。
学習と評価の部分は、train_gdbt_classifierという名前で関数化していますので、コピペでお使いいただけます。
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
def train_gbdt_classifier(df, target, columns, params={}, test_size=0.2, random_state=42):
"""
指定されたデータフレームとパラメータに基づいてGDBTを学習させ、レポートを出力する関数。
引数:
df : pandas.DataFrame
データを含むデータフレーム。
target : str
予測対象となるターゲット列名。
columns : list of str
使用する特徴量の列名のリスト。Targetが含まれていても無視する。
params : dict, optional (default={})
GDBTのハイパーパラメータ。
test_size : float, optional (default=0.2)
テストデータの割合。
random_state : int, optional (default=42)
乱数シード。
戻り値:
model : GradientBoostingClassifier
訓練されたGDBTモデルのオブジェクト。
cm : numpy.ndarray
混同行列を表す2次元配列。
"""
# 特徴量とターゲットに分ける(target 列を除外)
columns = [col for col in columns if col != target]
X = df[columns]
y = df[target]
# 訓練データとテストデータに分割する
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state)
# GBDT分類器のインスタンスを作成する
model = GradientBoostingClassifier(random_state=random_state, **params)
# モデルを訓練する
model.fit(X_train, y_train)
# テストデータで予測する
y_pred = model.predict(X_test)
# モデルの精度を評価する
accuracy = accuracy_score(y_test, y_pred)
report = classification_report(y_test, y_pred, target_names=[str(i) for i in range(len(df[target].unique()))])
cm = confusion_matrix(y_test, y_pred)
print(f'正解率: {accuracy}')
print('混同行列:')
print(cm)
print('分類レポート:')
print(report)
return model, cm
if __name__ == "__main__":
# データを読み込む
df = pd.read_csv('classification_data.csv')
# 関数の呼び出し(ハイパーパラメータはデフォルト値を使用)
model, cm = train_gbdt_classifier(df, target='正解データ', columns=df.columns)
# クラス名を設定して混同行列をプロット(プロット部分が必要なら別途追加)
class_names = df['正解データ'].unique().astype(str)正解率: 0.93
混同行列:
[[44 1 1 5]
[ 0 46 0 0]
[ 0 0 52 1]
[ 2 3 1 44]]
分類レポート:
precision recall f1-score support
0 0.96 0.86 0.91 51
1 0.92 1.00 0.96 46
2 0.96 0.98 0.97 53
3 0.88 0.88 0.88 50
accuracy 0.93 200
macro avg 0.93 0.93 0.93 200
weighted avg 0.93 0.93 0.93 200
ハイパーパラメータを指定する場合は、paramsに辞書形式で指定します。必要に応じて適宜値を書き換え、実行してください。
# 関数の呼び出し(ハイパーパラメータを指定)
train_gbdt_classifier(df, target='正解データ', columns=df.columns,params={'n_estimators': 100})分類結果(混同行列)の視覚化
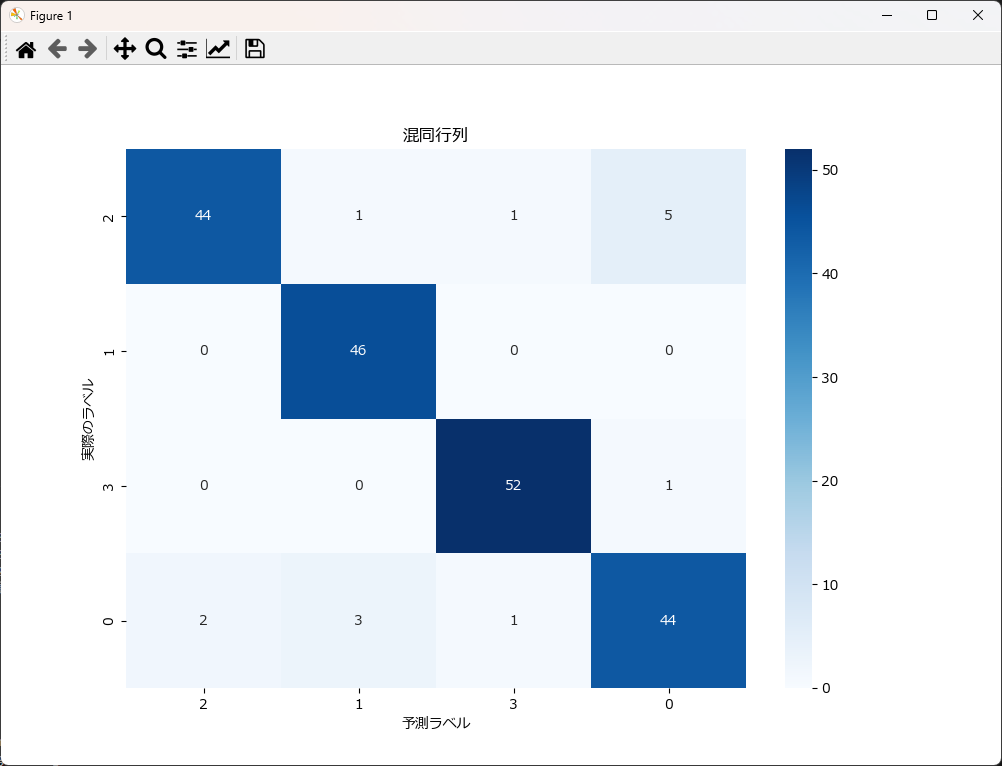
混同行列を可視化すると、結果が直感的に分かり易くなります。下記がそのサンプルです。 plot_confusion_matrixという関数名にしていますので、コピペで利用可能です。
#---------------------------------------------------------------
# この部分に、前述した train_gbdt_classifier関数 を張り付けて下さい
#---------------------------------------------------------------
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
def plot_confusion_matrix(cm, class_names=[]):
"""
混同行列をプロットする関数。
引数:
cm : numpy.ndarray
混同行列を表す2次元配列。
class_names : list of str, optional
クラス名のリスト。省略すると連番が表示される
"""
plt.figure(figsize=(10, 7))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues', xticklabels=class_names, yticklabels=class_names)
plt.xlabel('予測ラベル')
plt.ylabel('実際のラベル')
plt.title('混同行列')
plt.show()
if __name__ == "__main__":
# データを読み込む
df = pd.read_csv('classification_data.csv')
# 関数の呼び出し(ハイパーパラメータはデフォルト値を使用)
model, cm = train_gbdt_classifier(df, target='正解データ', columns=df.columns)
# クラス名を設定して混同行列をプロット
class_names = df['正解データ'].unique().astype(str)
plot_confusion_matrix(cm, class_names=class_names)分類結果の評価
今回のテストデータに対してGDBTで分類した結果を整理し、評価してみました。
正解率
| 正解率(Accuracy) | 0.93 |
|---|
モデルの全体的な精度は非常に高いと言えます。
混同行列
| 正解の分類クラス | クラス 0の予測件数 | クラス 1の予測件数 | クラス 2の予測件数 | クラス 3の予測件数 |
|---|---|---|---|---|
| クラス 0 | 44 | 1 | 1 | 5 |
| クラス 1 | 0 | 46 | 0 | 0 |
| クラス 2 | 0 | 0 | 52 | 1 |
| クラス 3 | 2 | 3 | 1 | 44 |
クラス0は誤分類が7件、クラス1は誤分類が0件、クラス2は誤分類が3件、クラス3は誤分類が5件であるため、高い精度で分類されていることが分かります。
分類レポート
| クラス | 適合率 (Precision) | 再現率 (Recall) | F1スコア (F1-Score) | サポート (Support) |
|---|---|---|---|---|
| 0 | 0.96 | 0.86 | 0.91 | 51 |
| 1 | 0.92 | 1.00 | 0.96 | 46 |
| 2 | 0.96 | 0.98 | 0.97 | 53 |
| 3 | 0.88 | 0.88 | 0.88 | 50 |
| クラス | 適合率 (Precision) | 再現率 (Recall) | F1スコア (F1-Score) | サンプル数 |
|---|---|---|---|---|
| 正解率(Accuracy) | - | - | 0.93 | 200 |
| マクロ平均 | 0.93 | 0.93 | 0.93 | 200 |
| 加重平均 | 0.93 | 0.93 | 0.93 | 200 |
分類レポートを見ると、全体的に非常に高い性能を発揮していることがわかります。
ただし、クラス 3 の適合率と再現率が他のクラスと比較するとやや低めであるため、パフォーマンスの均衡を保ちつつ、さらなる向上策を検討する余地があります。
また、クラス 0 の再現率が他のクラスより低く、見逃しが若干発生していることが懸念されます。この点については、クラス 0 のデータの増強や、モデルのハイパーパラメータの調整による改善が考えられます。
- クラス 0:
再現率がやや低く、実際のクラス 0 が見逃される可能性があります。 - クラス 1:
再現率が 1.00 であり、クラス 1 を正確に捉えていることを示しています。 - クラス 2:
適合率・再現率ともに高く、バランスの取れた分類性能を発揮しています。 - クラス 3:
他のクラスに比べ適合率・再現率が若干低いものの、全体としては良好な結果です。 - マクロ平均:
モデルがすべてのクラスで安定した分類性能を示していることが確認できます。 - 加重平均:
サンプル数の多いクラスの影響を考慮した評価であり、全体の分類精度を適切に反映しています。
GDBTによる回帰問題の解き方
事前準備(ライブラリ導入とデータ準備)
事前に下記3つのライブラリをインストールしてください。
pip install matplotlib
pip install pandas
pip install scikit-learn
下記は今回の回帰に使うダミーデータの生成プログラムです。7つの特徴量のデータとなります。
import numpy as np
import pandas as pd
# 特徴量の数
n_features = 7
# 各特徴量の標準偏差
std_devs = [1, 1, 1, 1, 1, 1, 1]
# 相関行列の設定(例: 1番目と2番目の特徴量が強い相関を持つ)
correlation_matrix = np.array([
[1, 0.8, 0.2, 0.1, 0.1, 0.1, 0.1],
[0.8, 1, 0.3, 0.2, 0.2, 0.2, 0.2],
[0.2, 0.3, 1, 0.4, 0.3, 0.3, 0.3],
[0.1, 0.2, 0.4, 1, 0.5, 0.5, 0.5],
[0.1, 0.2, 0.3, 0.5, 1, 0.4, 0.4],
[0.1, 0.2, 0.3, 0.5, 0.4, 1, 0.3],
[0.1, 0.2, 0.3, 0.5, 0.4, 0.3, 1]
])
# 共分散行列の計算
covariance_matrix = np.outer(std_devs, std_devs) * correlation_matrix
# ダミーデータの生成
np.random.seed(42)
n_samples = 1000
data = np.random.multivariate_normal(np.zeros(n_features), covariance_matrix, size=n_samples)
# DataFrameに変換
df = pd.DataFrame(data, columns=[f'特徴量_{i+1}' for i in range(n_features)])
# 結果の確認
print(df.head())
# CSVファイルに保存
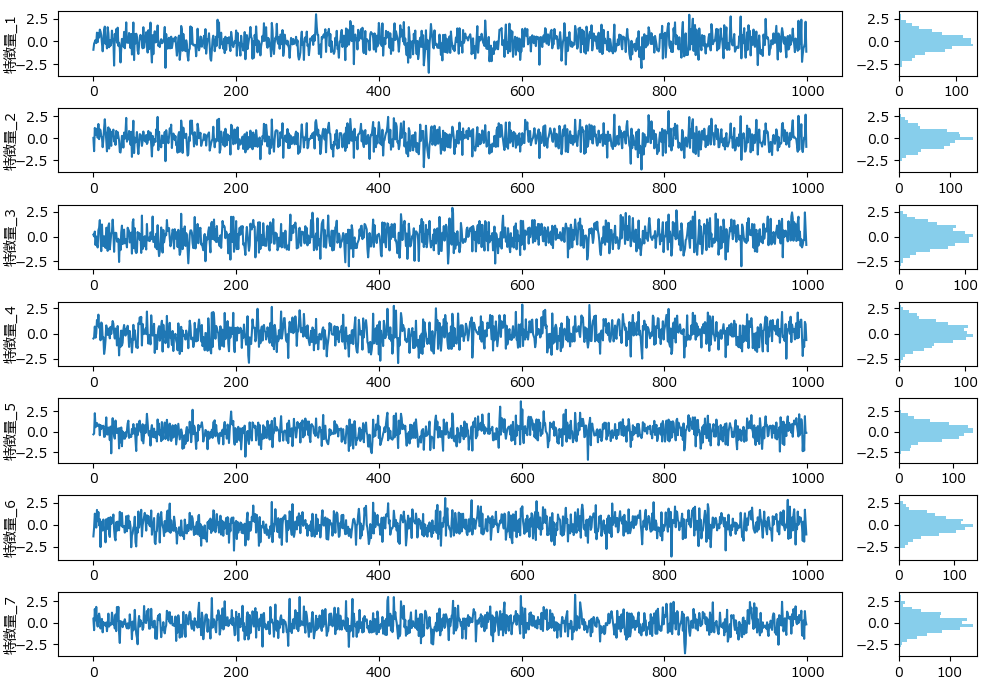
df.to_csv('regression_data.csv', index=False)下記のグラフは、分類モデル用データ生成で紹介したplot_features_with_histogramを使って描画しました。
GDBTによる回帰モデルの学習と評価(サンプルコードと解説)
以下は、GDBTを用いて回帰モデルの学習と評価を行うサンプルコードです。
実行すると学習が始まり、精度評価指標(統計情報、平均絶対誤差、平均二乗誤差、重要度など)が出力されます。
学習と評価の部分は、train_gbdt_regressorという名前で関数化していますので、コピペでお使いいただけます。
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score, mean_absolute_percentage_error
def train_gbdt_regressor(df, target, columns, params={}, test_size=0.2, random_state=42):
"""
指定されたデータフレームとパラメータに基づいてGBDTモデルを学習させ、レポートを出力する関数。
引数:
df : pandas.DataFrame
データを含むデータフレーム。
target : str
予測対象となるターゲット列名。
columns : list of str
使用する特徴量の列名のリスト。ターゲットが含まれていても無視する。
params : dict, optional (default={})
GBDTのハイパーパラメータ。
test_size : float, optional (default=0.2)
テストデータの割合。
random_state : int, optional (default=42)
乱数シード。
戻り値:
model : GradientBoostingRegressor
訓練されたGBDTモデルのオブジェクト。
y_test : list
テストに使った正解データ。
y_pred: list
予測した結果。
"""
# 特徴量とターゲットに分ける(target 列を除外)
columns = [col for col in columns if col != target]
X = df[columns]
y = df[target]
# 訓練データとテストデータに分割する
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state)
# GBDTモデルのインスタンスを作成する
model = GradientBoostingRegressor(random_state=random_state, **params)
# モデルを訓練する
model.fit(X_train, y_train)
# テストデータで予測する
y_pred = model.predict(X_test)
# モデルの精度を評価する
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse) # RMSE
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
mape = mean_absolute_percentage_error(y_test, y_pred)
# 統計情報を表示
print(f'{target}の統計情報:')
print(f'最小値(Min): {y.min()}')
print(f'最大値(Max): {y.max()}')
print(f'平均値(Mean): {y.mean()}')
print(f'標準偏差(Std): {y.std()}')
print(f'分散(Var): {y.var()}')
# 精度指標を出力する
print(f'平均絶対誤差 (Mean Absolute Error): {mae}')
print(f'平均二乗誤差 (Mean Squared Error): {mse}')
print(f'ルート平均二乗誤差 (Root Mean Squared Error): {rmse}')
print(f'平均絶対パーセンテージ誤差 (MAPE): {mape}')
print(f'決定係数 (R^2 Score): {r2}')
# 特徴量の重要度を表示する
feature_importances = model.feature_importances_
importance_df = pd.DataFrame({'特徴量 (Feature)': columns, '重要度 (Importance)': feature_importances})
importance_df = importance_df.sort_values(by='重要度 (Importance)', ascending=False)
print("\n特徴量の重要度:")
print(importance_df)
return model, y_test, y_pred
if __name__ == "__main__":
# データの読み込み
df = pd.read_csv('regression_data.csv')
# 特徴量_1 の予測モデルを作成する
model, y_test, y_pred = train_gbdt_regressor(df, '特徴量_1', df.columns)特徴量_1の統計情報:
最小値(Min): -3.4181790752853725
最大値(Max): 2.967258816333585
平均値(Mean): -0.018768452256335492
標準偏差(Std): 0.9893707041157269
分散(Var): 0.9788543901624494
平均絶対誤差 (Mean Absolute Error): 0.5135631328779169
平均二乗誤差 (Mean Squared Error): 0.422366022875417
ルート平均二乗誤差 (Root Mean Squared Error): 0.6498969325019291
平均絶対パーセンテージ誤差 (MAPE): 2.5279779380025276
決定係数 (R^2 Score): 0.6269102310593907
特徴量の重要度:
特徴量 (Feature) 重要度 (Importance)
0 特徴量_2 0.837562
5 特徴量_7 0.042185
1 特徴量_3 0.035135
4 特徴量_6 0.031959
3 特徴量_5 0.026935
2 特徴量_4 0.026225
回帰結果の可視化
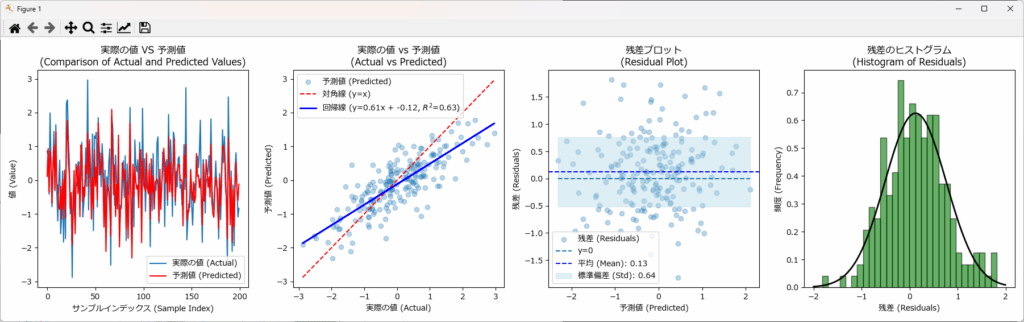
回帰結果を可視化することで、実際の値と予測値との差、残差のバラつき、残差の分布状態が直感的に把握できます。下記がそのサンプルです。 plot_figuresという関数名にしていますので、コピペで利用可能です。
#------------------------------------------------------------------------
# この部分に、前述した train_gbdt_regressor関数 を張り付けて下さい
#------------------------------------------------------------------------
from scipy.stats import norm
from sklearn.metrics import r2_score
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
def plot_figures(y_test, y_pred):
"""
グラフを描画し、指定されたファイル名で保存する関数
引数:
y_test : pandas.Series
実際の値
y_pred : numpy.ndarray
予測値
"""
# 残差の計算
residuals = y_test - y_pred
fig, axs = plt.subplots(1, 4, figsize=(18, 5))
# 実際の値と予測値の折れ線グラフ
axs[0].plot(y_test.values, label='実際の値 (Actual)', linestyle='-', marker=None)
axs[0].plot(y_pred, label='予測値 (Predicted)', color='red', linestyle='-', marker=None)
axs[0].set_xlabel('サンプルインデックス (Sample Index)')
axs[0].set_ylabel('値 (Value)')
axs[0].set_title('実際の値 VS 予測値\n(Comparison of Actual and Predicted Values)')
axs[0].legend()
# 実際の値と予測値の散布図
axs[1].scatter(y_test, y_pred, alpha=0.3, label='予測値 (Predicted)')
axs[1].plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', label='対角線 (y=x)')
# 回帰線の計算
slope, intercept = np.polyfit(y_test, y_pred, 1)
r2 = r2_score(y_test, y_pred)
axs[1].plot(y_test, slope * y_test + intercept, color='blue', linestyle='-', linewidth=2, label=f'回帰線 (y={slope:.2f}x + {intercept:.2f}, $R^2$={r2:.2f})')
axs[1].set_xlabel('実際の値 (Actual)')
axs[1].set_ylabel('予測値 (Predicted)')
axs[1].set_title('実際の値 vs 予測値\n(Actual vs Predicted)')
axs[1].legend()
# 残差プロット
axs[2].scatter(y_pred, residuals, alpha=0.3, label='残差 (Residuals)')
axs[2].hlines(y=0, xmin=y_pred.min(), xmax=y_pred.max(), linestyles='dashed', label='y=0')
# 残差の平均と標準偏差を計算
residuals_mean = np.mean(residuals)
residuals_std = np.std(residuals)
# y_pred をソートし、それに対応する範囲を再計算
sorted_indices = np.argsort(y_pred)
sorted_y_pred = y_pred[sorted_indices]
sorted_upper = residuals_mean + residuals_std
sorted_lower = residuals_mean - residuals_std
axs[2].axhline(y=residuals_mean, color='blue', linestyle='--', label=f'平均 (Mean): {residuals_mean:.2f}')
# 標準偏差の範囲を水色で塗りつぶし
axs[2].fill_between(
sorted_y_pred, # ソートされた予測値
sorted_lower, # 下限 (固定値)
sorted_upper, # 上限 (固定値)
color='lightblue',
alpha=0.4,
label=f'標準偏差 (Std): {residuals_std:.2f}'
)
axs[2].set_xlabel('予測値 (Predicted)')
axs[2].set_ylabel('残差 (Residuals)')
axs[2].set_title('残差プロット\n(Residual Plot)')
axs[2].legend()
# 残差のヒストグラム
axs[3].hist(residuals, bins=30, edgecolor='k', density=True, alpha=0.6, color='g')
# 残差のヒストグラムに正規分布曲線を追加
xmin, xmax = axs[3].get_xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, residuals_mean, residuals_std)
axs[3].plot(x, p, 'k', linewidth=2)
axs[3].set_xlabel('残差 (Residuals)')
axs[3].set_ylabel('頻度 (Frequency)')
axs[3].set_title('残差のヒストグラム\n(Histogram of Residuals)')
plt.tight_layout()
plt.show()
if __name__ == "__main__":
# データを読み込む
df = pd.read_csv('regression_data.csv')
# 関数の呼び出し(ハイパーパラメータはデフォルト値を使用)
model, y_test, y_pred = train_gbdt_regressor(df, target='特徴量_1', columns=df.columns)
# グラフを描画
plot_figures(y_test, y_pred)回帰結果の評価
精度の評価
| 指標 | 値 |
|---|---|
| 平均絶対誤差 (MAE) | 0.5135631328779169 |
| 平均二乗誤差 (MSE) | 0.422366022875417 |
| ルート平均二乗誤差 (RMSE) | 0.6498969325019291 |
| 平均絶対パーセンテージ誤差 (MAPE) | 2.5279779380025276 |
| 決定係数 (R^2 Score) | 0.6269102310593907 |
MAE、MSE、RMSE、MAPEはそれぞれ誤差の指標です。これを評価する前に、予測対象となる特徴量_1の統計情報を確認しておきましょう。
| 最小値 | 最大値 | 平均値 | 標準偏差 | 分散 |
|---|---|---|---|---|
| -3.4182 | 2.9673 | -0.01889 | 0.9894 | 0.9789 |
平均が0に近く、データの67%が-0.989~+0.989に分布しています。また最小は-3.42、最大は2.98 です。
このデータに対してMAE、MSE、RMSEは、それぞれ 0.51、0.42、0.65 となっており、かなり多くの誤差が含まれていることが分かります。
MAPEは2.2%と比較的小さな値ですが、MAPEの性質上、0付近のデータが多い場合は結果が不正確になるため、過小評価されている可能性が高いと考えられます。
また、決定係数の 0.627 は、それほど高い数値とは言えません。従って、このモデルの実務利用は厳しいと言えます。
次の3つ方法により、精度の改善を目指すべきです。
- ハイパーパラメータの調整: モデルの設定を最適化することで予測精度を向上させる。
- 特徴量の選択とエンジニアリング: 重要な特徴量を追加したり、不要な特徴量を削除する。
- データの前処理: 標準化やスケーリングを行い、モデルの性能を向上させる。
可視化の結果からも、誤差が多く精度が低いことが直感的に読み取れます。

特徴量の重要度
| 特徴量 (Feature) | 重要度 (Importance) |
|---|---|
| 特徴量_2 | 0.837562 |
| 特徴量_7 | 0.042185 |
| 特徴量_3 | 0.035135 |
| 特徴量_6 | 0.031959 |
| 特徴量_5 | 0.026935 |
| 特徴量_4 | 0.026225 |
GBDTでは、特徴量_1を予測する際に使った特徴量(2~7) において、予測にどの程度寄与したかを数値で表すことができます。
これを見ると、特徴量_2 の重要度が0.837562と最も高く、その他は0.1未満です。つまり今回のモデルは、ほぼ特徴量_2だけを使って予測していたことになります。試しに特徴量_2 だけで予測モデルを作成したとしても、予測精度はほとんど変わらないでしょう。
このように、重要度を確認することで、予測で使われていない特徴量を把握することができます。
ハイパーパラメータ
予測精度を向上させるには、ハイパーパラメータの調整が重要です。GDBTには数多くハイパーパラメータが用意されていますが、おおよそ下記の4種類が目安となります。
learning_rate:GBDTでは、各木の影響を抑えながら段階的に改善していくため、このパラメータは重要です。一般的には0.01~0.1の範囲 で設定し、決定木の数(n_estimators)と組み合わせて調整します。
n_estimators:増やすことでモデルの安定性が向上しますが、計算時間も増加します。一般的には100~500の範囲で調整します。ランダムフォレストより多めの木を使うことが多いです。
max_depth:過学習を防ぐために適切な深さを見つけることが重要です。デフォルトは無制限ですが、3~10の範囲で試してみるとよいでしょう。ランダムフォレストより浅めの深さにすることが多いです。
subsample:0.8~1.0 の範囲で試しながら調整します。1.0より小さくすると汎化性能が向上しやすいです。
max_features:sqrt(n_features) や log2(n_features) などの設定が一般的です。全特徴量の1/3~1/2程度を試してみるとよいでしょう。
GBDTの主要なハイパーパラメータ一覧
| パラメータ名 | 説明 | デフォルト値 |
|---|---|---|
| n_estimators | 決定木の数。各決定木が前の木の誤差を修正しながら学習するため、通常はランダムフォレストより多めに設定します。 | 100 |
| learning_rate | 各決定木の影響を調整するための係数。値を小さくすると汎化性能が向上しやすいですが、より多くの木が必要になります。 | 0.1 |
| max_depth | 各決定木の最大深さ。過学習を防ぐため、通常は 浅め(3~10程度) に設定されます。 | 3 |
| min_samples_split | ノードを分割するために必要なサンプルの最小数。過学習を防ぐために適切な値を設定します。 | 2 |
| min_samples_leaf | リーフノードに必要なサンプルの最小数。値を大きくすると過学習を抑えられます。 | 1 |
| max_features | 各決定木が分割に使用する特徴量の数。通常は sqrt(n_features) や log2(n_features) が使われます。 | "auto" |
| subsample | 各決定木が使用するデータの割合。値を 1.0 より小さくすると汎化性能が向上します。 | 1.0 |
| random_state | 乱数シードを設定し、モデルの再現性を確保します。 | None |
| verbose | 学習の進行状況を出力するレベル。0 は出力なし、1 は簡易出力、2 以上で詳細な進行状況が表示されます。 | 0 |
| warm_start | True にすると、前回の学習結果を利用しながら追加学習を行うことができます。 | False |
パラメータチューニング手法
ハイパーパラメータのチューニングで最もよく使われるグリッドサーチを使って、GDBTをチューニングする関数のサンプルです。
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score, mean_absolute_percentage_error
def grid_search_gbdt(df, target, columns, param_grid, test_size=0.2, random_state=42):
"""
グリッドサーチを使用してGBDTモデルのハイパーパラメータをチューニングし、最適なモデルを見つける関数。
引数:
df : pandas.DataFrame
データを含むデータフレーム。
target : str
予測対象となるターゲット列名。
columns : list of str
使用する特徴量の列名のリスト。ターゲットが含まれていても無視する。
param_grid : dict
グリッドサーチで試すハイパーパラメータの辞書。
test_size : float, optional (default=0.2)
テストデータの割合。
random_state : int, optional (default=42)
乱数シード。
戻り値:
best_model : GradientBoostingRegressor
最適なハイパーパラメータで訓練されたGBDTモデルのオブジェクト。
best_params : dict
最適なハイパーパラメータの辞書。
best_score : float
グリッドサーチで得られた最適なスコア。
"""
# 特徴量とターゲットに分ける(target 列を除外)
columns = [col for col in columns if col != target]
X = df[columns]
y = df[target]
# 訓練データとテストデータに分割する
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state)
# GBDTモデルのインスタンスを作成する
model = GradientBoostingRegressor(random_state=random_state)
# グリッドサーチを行う
grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=5, scoring='neg_mean_squared_error', n_jobs=-1)
grid_search.fit(X_train, y_train)
# 最適なモデルとパラメータを取得する
best_model = grid_search.best_estimator_
best_params = grid_search.best_params_
best_score = grid_search.best_score_
# テストデータで予測する
y_pred = best_model.predict(X_test)
# モデルの精度を評価する
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse) # RMSE
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
mape = mean_absolute_percentage_error(y_test, y_pred)
# 精度指標を出力する
print(f'最適なハイパーパラメータ: {best_params}')
print(f'グリッドサーチの最適なスコア: {best_score}')
print(f'平均絶対誤差 (Mean Absolute Error): {mae}')
print(f'平均二乗誤差 (Mean Squared Error): {mse}')
print(f'ルート平均二乗誤差 (Root Mean Squared Error): {rmse}')
print(f'平均絶対パーセンテージ誤差 (MAPE): {mape}')
print(f'決定係数 (R^2 Score): {r2}')
return best_model, best_params, best_score, y_test, y_pred
if __name__ == "__main__":
# 回帰問題用テストデータの読み込み
df = pd.read_csv('regression_data.csv')
param_grid = {
'n_estimators': [100, 200],
'learning_rate': [0.01, 0.1],
'max_depth': [3, 5, 10],
'min_samples_split': [2, 5],
'min_samples_leaf': [1, 2],
'subsample': [0.8, 1.0]
}
best_model, best_params, best_score, y_test, y_pred = grid_search_gbdt(df, target='特徴量_1', columns=df.columns, param_grid=param_grid)グリッドサーチを行った結果、平均絶対パーセンテージ誤差 (MAPE)の値が少しだけ改善されました。下記はその結果です。
最適なハイパーパラメータ: {'learning_rate': 0.01, 'max_depth': 3, 'min_samples_leaf': 1, 'min_samples_split': 5, 'n_estimators': 200, 'subsample': 0.8}
グリッドサーチの最適なスコア: -0.373133644639933
平均絶対誤差 (Mean Absolute Error): 0.5162336616363968
平均二乗誤差 (Mean Squared Error): 0.4255221933390507
ルート平均二乗誤差 (Root Mean Squared Error): 0.6523206215804087
平均絶対パーセンテージ誤差 (MAPE): 1.868928961090872
決定係数 (R^2 Score): 0.6241222821117036
GBDTが簡単に使える自作クラス
GBDTで分類と回帰のモデルを簡単に作成できるように、必要な機能をまとめたクラスを作りました。
下記に詳しい説明とソースコードを掲載しています。
コピペで使えるようになっていますので、是非ご活用下さい。
【コピペOK】ランダムフォレストやLightGBMを簡単に扱える自作クラスを紹介

まとめ
GBDT(Gradient Boosting Decision Trees)は、分類問題や回帰問題において高い予測精度を発揮し、過学習を抑えながら段階的に誤差を修正する強力な機械学習アルゴリズムです。
本記事では、GBDTの基本的な仕組みやメリット・デメリットを解説し、製造業での活用例や具体的な実装方法についても紹介しました。
また、分類や回帰における評価指標や特徴量の重要度解析、さらには効率的なハイパーパラメータチューニングの手法も取り上げました。これらを活用することで、実務においてGBDTを最適な形で導入し、高精度なモデルを構築することが可能になります。
GBDTは、柔軟な学習率調整や決定木の逐次的な改善により、難しいパターンのデータにも強く、幅広い用途で活用されています。
本記事が、みなさんのプロジェクトや課題解決に少しでも貢献できれば幸いです。









コメント