製造現場では、センサーデータ、製造ログ、品質検査データなど、膨大な時系列データが生成されています。これらのデータを的確に分析し、品質向上、歩留まり改善、異常検知、予知保全に繋げるためには、データの特性に合わせた効果的な可視化が鍵となります。
本記事では、製造業のデータ分析に特化し、時系列センサーデータの分布や周期性や変動などを把握するためのグラフ化(可視化)について、コピペで使えるサンプルコードとともにご紹介します。
値の変化を確認する(plot_features_with_histogram)
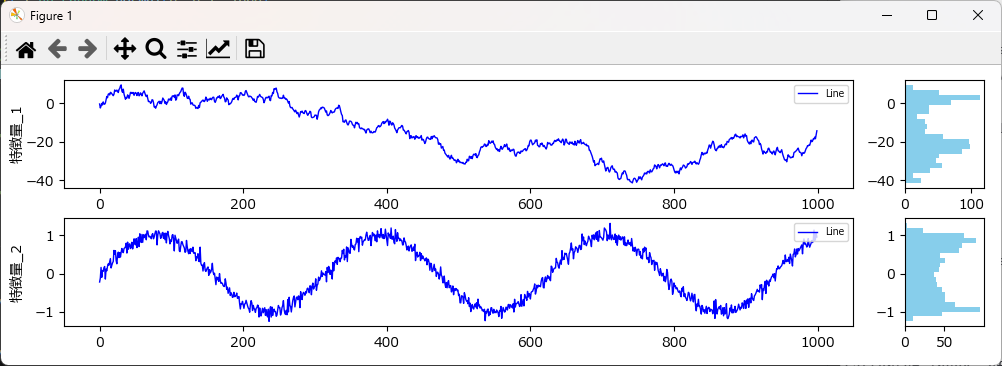
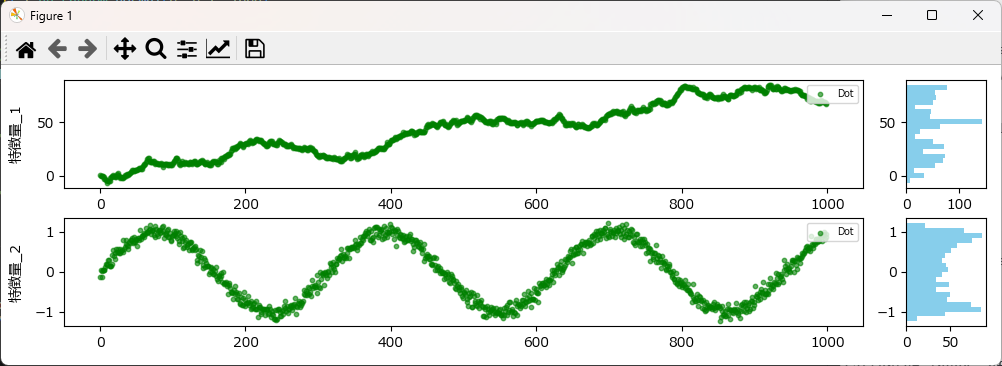
データが時間の経過に伴いどのように変化するかを、折れ線グラフ、又は点グラフで確認します。その際、右横にヒストグラムを描画しておくことで、値の分布も同時に確認できます。
plot_features_with_histogram 関数にDataFrameとグラフ化したいカラムのリストを渡すと、折れ線グラフが表示できます。
import matplotlib.pyplot as plt
from matplotlib import rcParams
# 日本語フォントの設定
rcParams['font.family'] = 'Meiryo'
def plot_features_with_histogram(df, columns, line_width=1.0, dot_size=0):
"""
指定されたデータフレームとカラムリストに基づいて、折れ線・散布図・ヒストグラムを描画する関数。
引数:
df : pandas.DataFrame
プロットするデータを含むデータフレーム。
columns : list of str
プロットする特徴量名のリスト。
line_width : float
折れ線の線幅(0を指定すると描画しない)。
dot_size : float
散布図の点サイズ(0を指定すると描画しない)。
"""
# グラフの設定
fig, axes = plt.subplots(len(columns), 2, figsize=(10, 1.5 * len(columns)),
gridspec_kw={'width_ratios': [10, 1], 'height_ratios': [1] * len(columns)})
for i, feature_name in enumerate(columns):
ax_plot = axes[i, 0]
# 折れ線グラフ(青)を描画
if line_width > 0:
ax_plot.plot(df.index, df[feature_name], linewidth=line_width, color='blue', label='Line')
# 散布図(オレンジ)を描画
if dot_size > 0:
ax_plot.scatter(df.index, df[feature_name], s=dot_size, color='green', alpha=0.6, label='Dot')
# 凡例
if (line_width > 0) or (dot_size > 0):
ax_plot.legend(loc='upper right', fontsize='x-small')
# ラベル設定
ax_plot.set_ylabel(feature_name)
ax_plot.yaxis.set_label_coords(-0.05, 0.5)
# ヒストグラム
axes[i, 1].hist(df[feature_name], bins=20, orientation='horizontal', color='skyblue')
plt.subplots_adjust(hspace=1.5, wspace=0.3, top=0.9, bottom=0.05, left=0.1, right=0.95)
plt.tight_layout(w_pad=1, h_pad=0.5)
plt.show()
# ===================== サンプル実行 ==========================
if __name__ == "__main__":
import pandas as pd
import numpy as np
df = pd.DataFrame({
"特徴量_1": np.random.randn(1000).cumsum(),
"特徴量_2": np.sin(np.linspace(0, 20, 1000)) + np.random.normal(0, 0.1, 1000)
})
# 折れ線と散布図の両方を表示(線幅1.5、点サイズ10)
plot_features_with_histogram(df, df.columns, line_width=1, dot_size=0)
# 折れ線のみ(点サイズ0)
# plot_features_with_histogram(df, df.columns, line_width=1.5, dot_size=0)
# 散布図のみ(線幅0)
# plot_features_with_histogram(df, df.columns, line_width=0, dot_size=8)
値の増減傾向を確認する(その1)
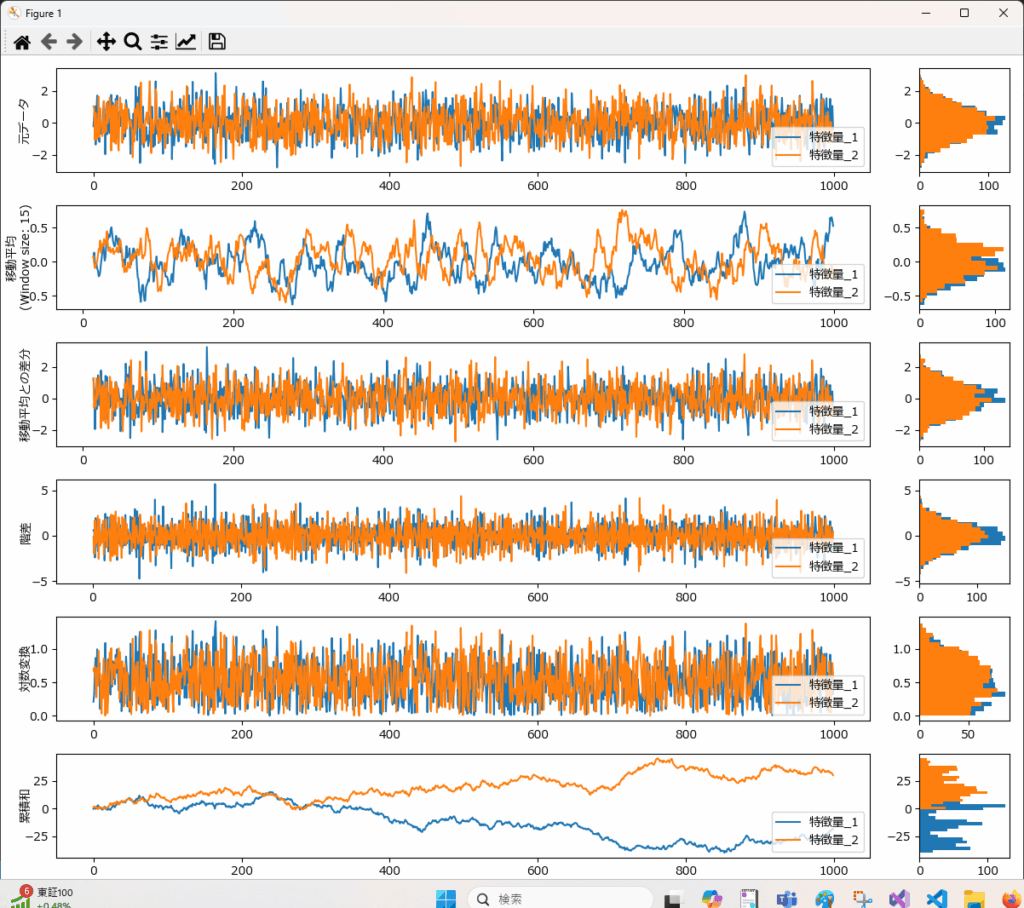
時系列データがどのように変化しているかを確認する際に、合わせてトレンドの有無や、増減の傾向を確認したい場合があります。一般的には、移動平均、移動平均との差分、階差、対数変換、累積和がよく用いられます。
| 指標 | 目的 | 得られる知見 |
|---|---|---|
| 移動平均 | ノイズを除去し、データの全体的な傾向を把握する | 長期的なトレンドを確認できる。短期の変動を平滑化し、周期的なパターンを検出しやすくする |
| 移動平均との差分 | データの変動が移動平均に対してどの程度大きいかを分析する | 価格変動や異常値を特定しやすくなる。特定の期間における急激な上昇・下降を検知 |
| 階差 | 連続するデータ間の変化率を調べる | 階差によりトレンドを排除することで、短期的な変動が強調される。これにより、急激な変化点の検出(例:市場の急変、機械の異常)がしやすくなる |
| 対数変換 | データのスケールを調整し、極端な変動を抑える | 変動の激しいデータでも分析しやすくなる。指数関数的な増加を直線的な関係に変換できる |
| 累積和 | 時系列データの蓄積量を可視化する | データの総変動量や累積変化を把握できる。継続的な成長・減少傾向の確認に有効 |
plot_transformed_features関数にDataFrameとグラフ化したいカラムのリストを渡すと、移動平均、移動平均との差分、階差、対数変換、累積和を縦に並べて描画します。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
# 日本語フォントの設定
rcParams['font.family'] = 'Meiryo'
# 修正版のグラフ描画関数(ヒストグラム追加)
def plot_transformed_features(df, columns, window_size=10, show_legend=True, legend_loc="upper left"):
"""
指定された特徴量の元データ、移動平均、移動平均との差分、階差、対数変換、累積和を描画し、各グラフの横にヒストグラムを追加する関数。
引数:
df : pandas.DataFrame
プロットするデータを含むデータフレーム。
columns : list of str
プロットする特徴量名のリスト。
window_size : int, デフォルト=10
移動平均のウィンドウサイズ。
show_legend : bool, デフォルト=True
凡例を表示するかどうか。
legend_loc : str, デフォルト="upper left"
凡例の位置(例: "upper right", "lower left", "best" など)。
"""
# タイトルを定義(移動平均はWindowサイズを改行して表示)
titles = [
"元データ",
f"移動平均\n(Window size: {window_size})",
"移動平均との差分",
"階差",
"対数変換",
"累積和"
]
num_plots = len(titles)
# グラフの設定(ヒストグラム用のサブプロットを追加)
fig, axes = plt.subplots(num_plots, 2, figsize=(12, 10),
gridspec_kw={'width_ratios': [9, 1], 'height_ratios': [1] * num_plots})
for i, title in enumerate(titles):
for column in columns:
if i == 0:
data = df[column] # 元データ
elif i == 1:
data = df[column].rolling(window=window_size).mean() # 移動平均
elif i == 2:
data = df[column] - df[column].rolling(window=window_size).mean() # 移動平均との差分
elif i == 3:
data = df[column].diff() # 階差
elif i == 4:
data = np.log(df[column].abs() + 1) # 対数変換(負の値を防ぐため+1)
elif i == 5:
data = df[column].cumsum() # 累積和
# 折れ線グラフ
axes[i, 0].plot(df.index, data, linestyle='-', marker=None, label=column)
axes[i, 0].set_ylabel(title)
axes[i, 0].yaxis.set_label_coords(-0.03, 0.5)
# ヒストグラム(右側)
axes[i, 1].hist(data.dropna(), bins=20, orientation='horizontal')
# 凡例の表示設定
if show_legend:
axes[i, 0].legend(loc=legend_loc)
plt.xlabel("Index")
plt.subplots_adjust(hspace=1.0, wspace=0.5)
plt.tight_layout()
plt.show()
# ===================== 使い方のサンプル ==========================
if __name__ == "__main__":
import pandas as pd
import numpy as np
# サンプルデータの生成
df = pd.DataFrame({"特徴量_1": np.random.randn(1000), "特徴量_2": np.random.randn(1000)})
# グラフ描画関数の呼び出し(例として特徴量_1, 特徴量_2を指定し、ウィンドウサイズ15、凡例を右下に表示)
plot_transformed_features(df, ["特徴量_1", "特徴量_2"], window_size=15, show_legend=True, legend_loc="lower right")値の増減傾向を確認する(その2)
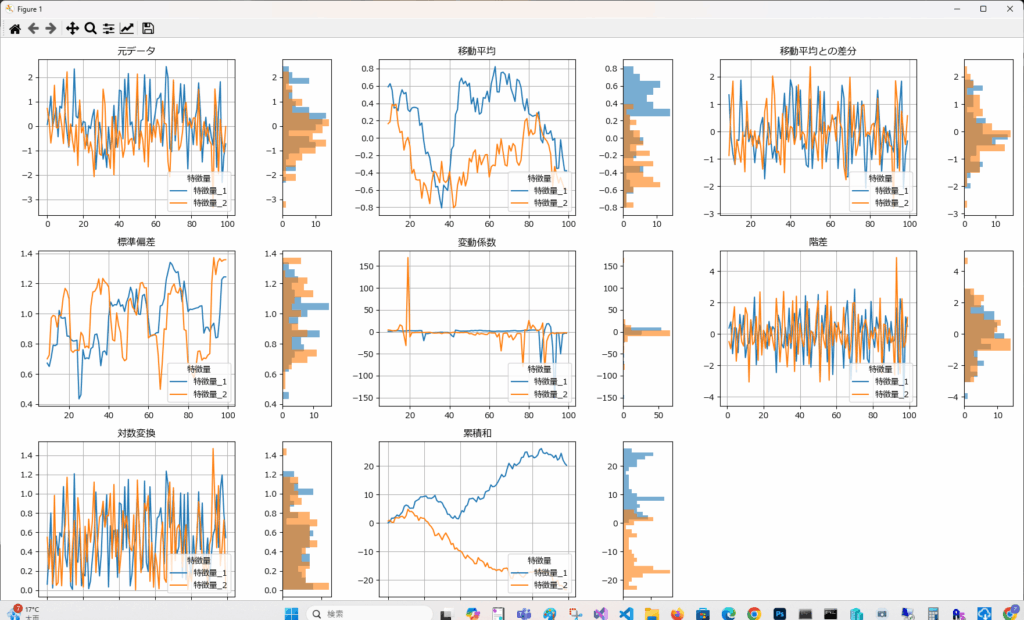
DataVisualizerクラスは、前述のグラフに標準偏差と変動係数を加えるとともに、指定した行数と列数でグラフを描画します。前述したplot_transformed_featuresよりもレイアウトが柔軟な分だけ、指定する引数が増えています。
| 指標 | 目的 | 得られる知見 |
|---|---|---|
| 標準偏差 | ばらつきの大きさを評価する | データの不安定性を検知し、異常値やノイズの強さを把握できる。市場変動や機械の故障リスク分析に役立つ |
| 変動係数 | 標準偏差を平均値で割り、変動の相対的な大きさを評価する | 単位が異なる特徴量間の比較が可能。安定しているセンサーや市場の価格動向を分析できる |
# ★★★★★★★★★
# この部分に、後述する DataVisualizer を張り付けて下さい。
# ★★★★★★★★★
# ===================== 使い方のサンプル ==========================
if __name__ == "__main__":
# サンプルデータ
df = pd.DataFrame({"特徴量_1": np.random.randn(100), "特徴量_2": np.random.randn(100)})
# 計算式リスト(辞書形式でタイトル、計算ロジック、プロットタイプ、ヒストグラム表示有無を統合)
functions = {
"元データ": {"func": lambda x: x, "plot": "line", "hist": True},
"移動平均": {"func": lambda x: x.rolling(window=10).mean(), "plot": "line", "hist": True},
"移動平均との差分": {"func": lambda x: x - x.rolling(window=10).mean(), "plot": "line", "hist": True},
"標準偏差": {"func": lambda x: x.rolling(window=10).std(), "plot": "line", "hist": True},
"変動係数": {"func": lambda x: x.rolling(window=10).std() / x.rolling(window=10).mean(), "plot": "line", "hist": True},
"階差": {"func": lambda x: x.diff(), "plot": "line", "hist": True},
"対数変換": {"func": lambda x: np.log(np.abs(x) + 1), "plot": "line", "hist": True},
"累積和": {"func": lambda x: x.cumsum(), "plot": "line", "hist": True},
}
# インスタンス生成
visualizer = DataVisualizer(functions, nrows=3, ncols=3, hist_width=2, show_legend=True, legend_loc="lower right", show_grid=True)
# グラフ描画
visualizer.plot_graphs(df, ["特徴量_1","特徴量_2"])分布と周期性を確認する
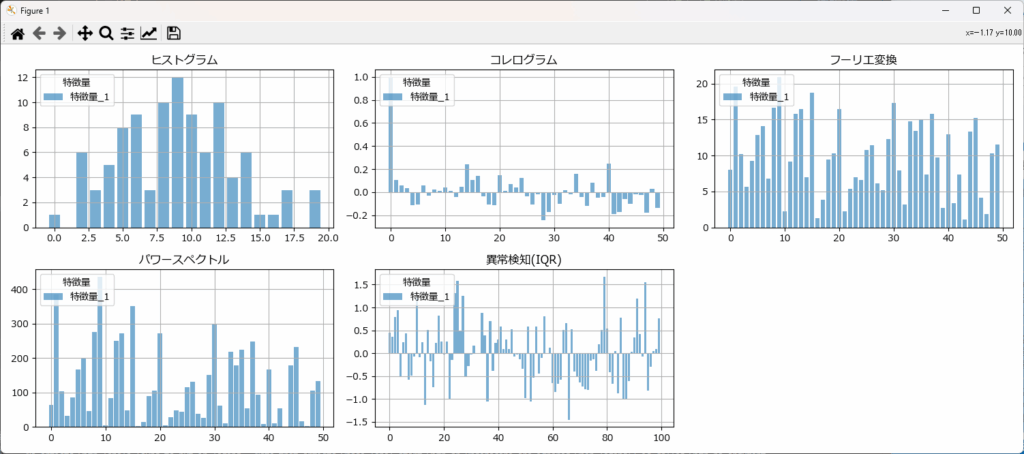
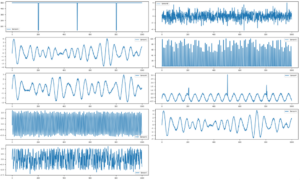
特徴量がどのような分布を持ち、どのような周期的な変動を示すかを把握するため有効なのが棒グラフです。DataVisualizerクラスは、ヒストグラムで分布を、コレログラム、フーリエ変換、パワースペクトル、異常検知(IQR)で周期的な変動をグラフ化します。
| 指標 | 目的 | 得られる知見 |
|---|---|---|
| ヒストグラム | データの分布を可視化 | 値の頻度を視覚化し、異常値や偏りの有無を確認できる。正規分布かどうかを判断する手がかりになる |
| コレログラム | 時系列データの周期性を分析 | データの自己相関を確認し、繰り返しパターンや周期的な変動を検出できる。市場動向や機械の動作サイクルを解析するのに有効 |
| フーリエ変換(FFT) | 時系列データの周波数成分を抽出 | 高周波・低周波成分を特定し、周期的な変動の要因を分析できる。振動解析や音響データ、信号処理に活用される |
| パワースペクトル | 信号のエネルギー分布を分析 | 各周波数成分が持つ影響度(パワー)を評価し、主要な周波数帯域を特定できる。機械の異常検知や振動特性の把握に活用 |
| 異常検知(IQR) | 外れ値を検出する | 四分位範囲を用いて異常値を特定し、異常が発生しやすいタイミングや要因を分析できる。製造ラインの品質管理や市場の急変動検出に活用 |
# ★★★★★★★★★
# この部分に、後述する DataVisualizer を張り付けて下さい。
# ★★★★★★★★★
# ===================== 使い方のサンプル ==========================
if __name__ == "__main__":
# サンプルデータ
df = pd.DataFrame({"特徴量_1": np.random.randn(100), "特徴量_2": np.random.randn(100)})
# 棒グラフに適した関数
MAX_LAG = 50 # コレログラムの最大ラグ
SAMPLING_RATE = 100 # FFTのサンプリングレート(例:100Hz)
functions = {
"ヒストグラム": {"func": lambda x: pd.Series(np.histogram(x.dropna(), bins=20)[0], index=range(20)), "plot": "bar", "hist": False}, # ヒストグラムは棒グラフで表示、ヒストグラムは重ねない
"コレログラム": {"func": lambda x: pd.Series([x.autocorr(lag=i) for i in range(MAX_LAG)], index=range(MAX_LAG)), "plot": "bar", "hist": False}, # コレログラムは折れ線グラフで表示、ヒストグラムは不要
"フーリエ変換": {"func": lambda x: pd.Series(
np.abs(np.fft.fft(x.dropna()))[:len(x)//2],
index=np.fft.fftfreq(len(x), d=1/SAMPLING_RATE)[:len(x)//2]
), "plot": "bar", "hist": False}, # フーリエ変換は折れ線グラフで表示、ヒストグラムも表示
"パワースペクトル": {"func": lambda x: pd.Series(
np.abs(np.fft.fft(x.dropna()))[:len(x)//2]**2,
index=np.fft.fftfreq(len(x), d=1/SAMPLING_RATE)[:len(x)//2]
), "plot": "bar", "hist": False}, # パワースペクトルは折れ線グラフで表示、ヒストグラムも表示
"異常検知(IQR)": {"func": lambda x: pd.Series(
(x - x.median()) / (x.quantile(0.75) - x.quantile(0.25)), index=x.index
), "plot": "bar", "hist": False}, # 異常検知は折れ線グラフで表示、ヒストグラムも表示
}
# インスタンス生成
visualizer = DataVisualizer(functions, nrows=2, ncols=3, hist_width=2, show_legend=True, legend_loc="lower right", show_grid=True)
# グラフ描画
visualizer.plot_graphs(df, ["特徴量_1"])ラグプロットで自己相関を確認する
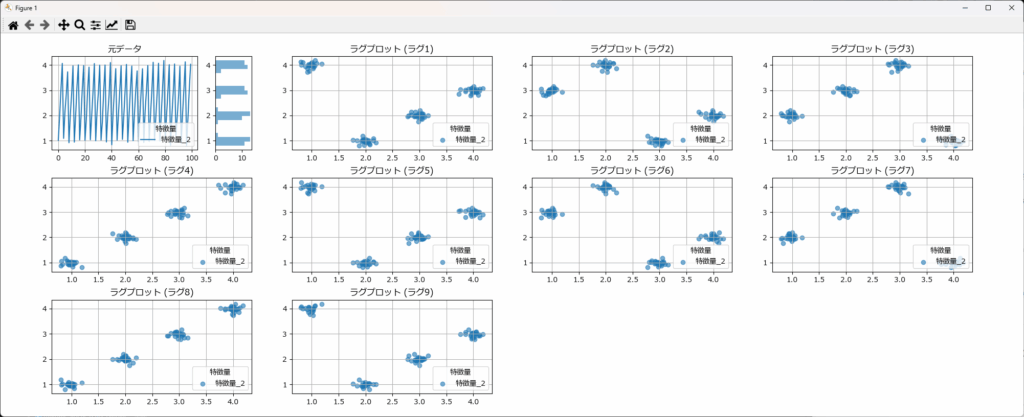
ラグプロットでは、時系列データの現在の値(横軸)と、ある一定のラグ(時間的なずれ)後の値(縦軸)を散布図としてプロットします。DataVisualizerクラスはラグプロットを簡単に描画できるため、どのような自己相関が存在するかを直感的に理解することができます。
| 項目 | ラグプロット (Lag Plot) | コレログラム (Correlogram / ACF Plot) |
|---|---|---|
| 表現形式 | 散布図 | 棒グラフ |
| 縦軸 | ラグ後の値 | 自己相関係数(数値) |
| 横軸 | 現在の値 | ラグの数 |
| 主な焦点 | 個々のデータポイントの関係性の視覚的評価 | 各ラグにおける自己相関の強さの数値的評価と統計的判断 |
| わかること | 自己相関のパターン、非線形性、外れ値、周期性の視覚的把握 | 自己相関の強さのラグ依存性、有意なラグ、周期性の示唆、時系列モデル選択のヒント |
| 強み | 関係性の形状を直感的に捉えやすい | 自己相関の強さを数値で比較でき、統計的な判断が可能 |
| 弱み | 自己相関の強さを数値で直接比較しにくい | 非線形な関係や個々のデータのばらつきを捉えにくい |
# ★★★★★★★★★
# この部分に、後述する DataVisualizer を張り付けて下さい。
# ★★★★★★★★★
# ===================== 使い方のサンプル ==========================
if __name__ == "__main__":
# サンプルデータ
pattern = [1, 2, 3, 4]
# データ長
data_length = 100
# パターンを繰り返した配列を作成
base_pattern = np.tile(pattern, data_length // len(pattern) + 1)[:data_length]
# 加えるランダムなノイズを生成 (平均0、標準偏差を指定)
noise_scale = 0.1 # ノイズの大きさを調整
random_noise = np.random.randn(data_length) * noise_scale
# ベースパターンにノイズを加算
noisy_feature_2 = base_pattern + random_noise
# DataFrame を作成
df = pd.DataFrame({
"特徴量_1": np.random.randn(100),
"特徴量_2": noisy_feature_2
})
functions = {
"元データ": {"func": lambda x: x, "plot": "line", "hist": True}
}
# ラグ 1 から 10 までのラグプロット関数を追加 (shift() を使用)
for lag in range(1, 10):
functions[f"ラグプロット (ラグ{lag})"] = {
"func": lambda x, l=lag: (x, x.shift(l)), # 現在の値と l 期前の値をペアにする
"plot": "scatter",
"hist": False
}
# インスタンス生成
visualizer = DataVisualizer(functions, nrows=3, ncols=4, hist_width=2, show_legend=True, legend_loc="lower right", show_grid=True)
# グラフ描画
visualizer.plot_graphs(df, ["特徴量_2"])総当たりの散布図で相関を確認する
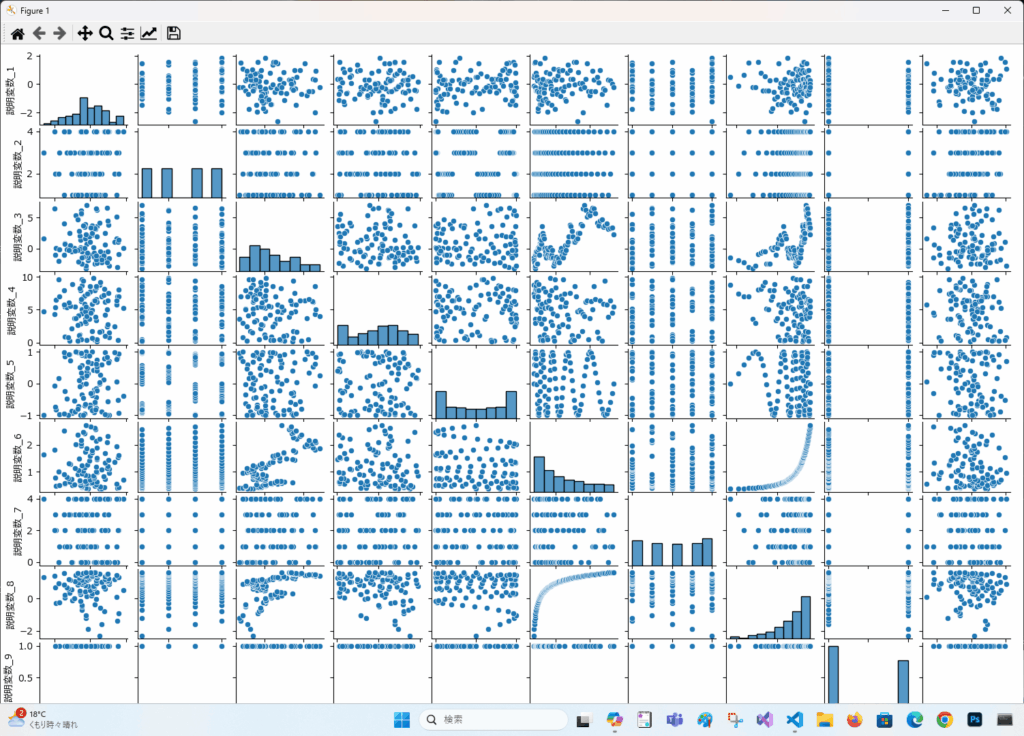
plot_all_column_pairsを使うと、DataFrame内の指定したカラムに対して、総当たりで散布図を描画することができます。
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
def plot_all_column_pairs(df, columns=None, fig_width=15, fig_height=12, **kwargs):
"""
指定された DataFrame のカラムについて、総当たりの散布図(ペアプロット)を描画します。
Args:
df (pd.DataFrame): 描画するデータを含む DataFrame。
columns (list of str, optional): 描画に使用するカラム名のリスト。
省略した場合、DataFrame の全カラムが対象となります。
fig_width (int or float, optional): Figure の幅(インチ)。デフォルトは 15。
fig_height (int or float, optional): Figure の高さ(インチ)。デフォルトは 12。
**kwargs: seaborn.pairplot に渡される追加のキーワード引数。
例:hue, diag_kind, markers, palette など。
"""
if columns is None:
columns = df.columns.tolist()
sns.pairplot(df[columns], **kwargs)
plt.gcf().set_size_inches(fig_width, fig_height) # Figure サイズを調整
plt.suptitle("Pairplot of Columns", y=1.02)
plt.tight_layout(h_pad=1.0, w_pad=1.0) # デフォルトより余白を大きく
plt.show()
# ===================== 使い方のサンプル ==========================
if __name__ == "__main__":
# サンプルデータ (以前と同じ)
np.random.seed(42)
num_samples = 100
df = pd.DataFrame({
"説明変数_1": np.random.randn(num_samples),
"説明変数_2": np.tile([1, 2, 3, 4], num_samples // 4),
"説明変数_3": np.cumsum(np.random.randn(num_samples)),
"説明変数_4": np.random.rand(num_samples) * 10,
"説明変数_5": np.sin(np.linspace(0, 10 * np.pi, num_samples)),
"説明変数_6": np.exp(np.linspace(-1, 1, num_samples)),
"説明変数_7": np.random.randint(0, 5, num_samples),
"説明変数_8": np.log(np.linspace(0.1, 5, num_samples)),
"説明変数_9": (np.random.rand(num_samples) > 0.5).astype(int), # 0 or 1
"説明変数_10": np.random.normal(loc=2, scale=0.5, size=num_samples)
})
# 特定のカラムのみで総当たり散布図を描画
plot_all_column_pairs(df, columns=df.columns, fig_width=12, fig_height=10)簡単グラフ描画クラス(DataVisualizer)
「値の増減傾向を確認する(その2)」、「分布と周期性を確認する」、「ラグプロットで自己相関を確認する」 のグラフを描画するための共通クラスのソースコードです。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import rcParams
import math
import matplotlib.gridspec as gridspec
rcParams['font.family'] = 'Meiryo'
class DataVisualizer:
"""
様々な関数を適用したデータの折れ線グラフ、散布図、棒グラフとヒストグラムを並べて表示するクラスです。
"""
def __init__(self, functions, nrows=None, ncols=None, hist_width=2,
show_legend=True, legend_loc="upper left", show_grid=True):
"""
DataVisualizer のコンストラクタ。
Args:
functions (dict): 適用する関数を定義した辞書。
キーはグラフのタイトル、値は以下のキーを持つ辞書です。
- 'func' (callable): データを変換する関数。Pandas Series を受け取り、
Pandas Series または (x, y) のタプルを返します(散布図の場合)。
- 'plot' (str, optional): グラフの種類 ('line', 'scatter', 'bar')。デフォルトは 'line'。
- 'hist' (bool, optional): ヒストグラムを表示するかどうか。デフォルトは True。
nrows (int, optional): グラフの行数。None の場合は自動計算。デフォルトは None。
ncols (int, optional): グラフの列数。None の場合は自動計算。デフォルトは None。
hist_width (int, optional): ヒストグラムの幅の比率。デフォルトは 2。
show_legend (bool, optional): 凡例を表示するかどうか。デフォルトは True。
legend_loc (str, optional): 凡例の位置。Matplotlib の legend 関数の loc 引数に準拠。
デフォルトは "upper left"。
show_grid (bool, optional): グリッド線を表示するかどうか。デフォルトは True。
"""
self.functions = functions
self.num_funcs = len(self.functions)
if nrows is None or ncols is None:
ncols = 2 if ncols is None else ncols
nrows = math.ceil(self.num_funcs / ncols)
self.nrows = nrows
self.ncols = ncols
self.hist_width = hist_width
self.show_legend = show_legend
self.legend_loc = legend_loc
self.show_grid = show_grid
def apply_functions(self, df, columns):
"""
指定された DataFrame の列に対して、登録された関数を適用し、変換後のデータを DataFrame として返します。
Args:
df (pd.DataFrame): 処理対象の DataFrame。
columns (list of str): 処理する列名のリスト。
Returns:
pd.DataFrame: 変換後のデータを含む DataFrame。
変換に失敗した場合は、NaN で埋められた Series が格納されます。
散布図の場合は、'_x' と '_y' がサフィックスとして追加された列名になります。
"""
transformed = {}
for col in columns:
for name, spec in self.functions.items():
func = spec["func"]
plot_type = spec.get("plot", "line")
try:
result = func(df[col])
if plot_type == "scatter" and isinstance(result, tuple):
x, y = result
transformed[f"{col}_{name}_x"] = pd.Series(x, index=df.index)
transformed[f"{col}_{name}_y"] = pd.Series(y, index=df.index)
else:
if not isinstance(result, pd.Series):
result = pd.Series(result, index=df.index)
transformed[f"{col}_{name}"] = result
except Exception as e:
print(f"エラー: {col} - {name} → {e}")
if plot_type == "scatter":
transformed[f"{col}_{name}_x"] = pd.Series([np.nan]*len(df), index=df.index)
transformed[f"{col}_{name}_y"] = pd.Series([np.nan]*len(df), index=df.index)
else:
transformed[f"{col}_{name}"] = pd.Series([np.nan]*len(df), index=df.index)
return pd.DataFrame(transformed)
def _plot_line(self, ax_line, ax_hist, transformed_df, func_name, col, show_hist):
"""
折れ線グラフを描画するヘルパーメソッド。
Args:
ax_line (matplotlib.axes.Axes): 折れ線グラフを描画する Axes オブジェクト。
ax_hist (matplotlib.axes.Axes or None): ヒストグラムを描画する Axes オブジェクト(表示しない場合は None)。
transformed_df (pd.DataFrame): 変換後のデータを含む DataFrame。
func_name (str): 現在処理中の関数の名前(グラフのタイトルに使用)。
col (str): 現在処理中の元の列名(凡例に使用)。
show_hist (bool): ヒストグラムを表示するかどうか。
"""
key = f"{col}_{func_name}"
data = transformed_df[key].dropna()
if not data.empty:
ax_line.plot(data.index, data, label=col)
if show_hist and ax_hist is not None:
ax_hist.hist(data, bins=20, orientation="horizontal", alpha=0.6, label=col)
def _plot_scatter(self, ax_line, ax_hist, transformed_df, func_name, col, show_hist):
"""
散布図を描画するヘルパーメソッド。
Args:
ax_line (matplotlib.axes.Axes): 散布図を描画する Axes オブジェクト。
ax_hist (matplotlib.axes.Axes or None): ヒストグラムを描画する Axes オブジェクト(表示しない場合は None)。
transformed_df (pd.DataFrame): 変換後のデータを含む DataFrame。
func_name (str): 現在処理中の関数の名前(グラフのタイトルに使用)。
col (str): 現在処理中の元の列名(凡例に使用)。
show_hist (bool): ヒストグラムを表示するかどうか。
"""
x_key = f"{col}_{func_name}_x"
y_key = f"{col}_{func_name}_y"
x = transformed_df[x_key].dropna()
y = transformed_df[y_key].dropna()
mask = x.index.intersection(y.index)
if not mask.empty:
ax_line.scatter(x.loc[mask], y.loc[mask], label=col, alpha=0.6)
if show_hist and ax_hist is not None:
ax_hist.hist(y.loc[mask], bins=20, orientation="horizontal", alpha=0.6, label=col)
def _plot_bar(self, ax_line, ax_hist, transformed_df, func_name, col, show_hist):
"""
棒グラフを描画するヘルパーメソッド。
Args:
ax_line (matplotlib.axes.Axes): 棒グラフを描画する Axes オブジェクト。
ax_hist (matplotlib.axes.Axes or None): ヒストグラムを描画する Axes オブジェクト(表示しない場合は None)。
transformed_df (pd.DataFrame): 変換後のデータを含む DataFrame。
func_name (str): 現在処理中の関数の名前(グラフのタイトルに使用)。
col (str): 現在処理中の元の列名(凡例に使用)。
show_hist (bool): ヒストグラムを表示するかどうか。
"""
key = f"{col}_{func_name}"
data = transformed_df[key].dropna()
if not data.empty:
ax_line.bar(data.index, data, label=col, alpha=0.6)
if show_hist and ax_hist is not None:
ax_hist.hist(data, bins=20, orientation="horizontal", alpha=0.6, label=col)
def plot_graphs(self, df, columns):
"""
登録された関数を適用したデータに対して、指定された種類のグラフとヒストグラムを並べて表示します。
Args:
df (pd.DataFrame): 描画する元のデータを含む DataFrame。
columns (list of str): 描画する列名のリスト。
"""
transformed_df = self.apply_functions(df, columns)
# fig のサイズを設定。subplotのサイズで計算しているが、figsize=(10,10)の様に固定で指定しても良い
subplot_x_size = 5
subplot_y_size = 2.5
fig = plt.figure(figsize=(subplot_x_size * self.ncols, subplot_y_size * self.nrows))
# subplotの上下左右の余白(wspace,hspace)を設定
outer_grid = gridspec.GridSpec(self.nrows, self.ncols, wspace=0.2, hspace=0.3)
for i, (func_name, spec) in enumerate(self.functions.items()):
row_index = i // self.ncols
col_index = i % self.ncols
show_hist = spec.get("hist", True)
plot_type = spec.get("plot", "line")
inner_grid = gridspec.GridSpecFromSubplotSpec(1, 2 if show_hist else 1,
subplot_spec=outer_grid[row_index, col_index],
wspace=0.0 if not show_hist else 0.2,
width_ratios=[8, self.hist_width] if show_hist else [1])
ax_line = fig.add_subplot(inner_grid[0, 0])
ax_hist = fig.add_subplot(inner_grid[0, 1]) if show_hist else None
for col in columns:
if plot_type == "line":
self._plot_line(ax_line, ax_hist, transformed_df, func_name, col, show_hist)
elif plot_type == "scatter":
self._plot_scatter(ax_line, ax_hist, transformed_df, func_name, col, show_hist)
elif plot_type == "bar":
self._plot_bar(ax_line, ax_hist, transformed_df, func_name, col, show_hist)
ax_line.set_title(func_name)
if self.show_grid:
ax_line.grid(True)
if self.show_legend:
ax_line.legend(loc=self.legend_loc, title="特徴量")
if not show_hist and ax_hist is not None:
fig.delaxes(ax_hist)
plt.subplots_adjust(hspace=0.3, wspace=0.2, top=0.94, bottom=0.06, left=0.05, right=0.95)
plt.tight_layout(w_pad=0.5, h_pad=0.3)
plt.show()まとめ
本記事では、製造業におけるデータ分析に焦点を当て、センサーデータのグラフ化の方法についてご紹介しました。
- 品質指標の変動と分布 を可視化する折れ線グラフとヒストグラム
- 異常兆候を捉える ためのトレンド分析グラフ(移動平均、階差など)
- 設備の周期性や異常パターン を分析するコレログラム、フーリエ変換
- 異常伝播や原因特定 に役立つラグプロット
- 品質特性と製造条件の関連性 を探索する総当たり散布図
今回ご紹介した内容に加え、 DataVisualizer クラスや plot_all_column_pairs 関数が、製造現場に蓄積されたデータの可視化に貢献できれば幸いです。


コメント