機械学習のアルゴリズムにはさまざまな選択肢がありますが、「高い予測精度を維持しながら、計算コストを抑え、大規模データやカテゴリデータにも対応したい!」そんな場面で頼れるのが AdaBoost です。
AdaBoost(Adaptive Boosting)は、弱学習器を組み合わせて強力な分類器を構築するアンサンブル学習の一種です。特に、誤分類されたデータに重点を置きながら学習を進めることで、精度を向上させる仕組みになっています。一般的なブースティング手法とは異なり、各学習器の重みを調整しながら最適なモデルを構築できるため、過学習を抑えつつ高精度な予測を実現します。
本記事では、AdaBoostを活用して分類問題と回帰問題を解く方法を、サンプルコード付きで分かりやすく解説します。
Pythonでの実装方法はもちろん、ランダムフォレストや他のブースティング手法(XGBoost、LightGBM、CatBoost など)との違い、メリット・デメリット、パラメータチューニングのポイントまで幅広く網羅していますので、AdaBoostを使ってモデルを改善したい方は、ぜひご一読ください!
AdaBoostとは
AdaBoost(Adaptive Boosting) は、弱学習器を組み合わせて強力な分類器を構築するアンサンブル学習の一種であり、高精度な予測を実現できる点が特徴です。
AdaBoostは、決定木や線形分類器などの弱学習器を活用し、回帰や分類など幅広い問題に対応可能です。複数の学習器を直列につなげて学習を進めることで、誤分類されたデータに重点を置きながら、精度の高い予測モデルを構築します。さらに、各学習器の重みを調整しながら最適なモデルを構築できるため、過学習を抑えつつ高精度な予測を実現します。
また、AdaBoostの大きな特徴として、データの前処理を工夫することで、カテゴリ変数を含むデータにも適用可能な点が挙げられます。例えば、One-Hot EncodingやLabel Encodingを用いることで、カテゴリ変数を数値化し、AdaBoostの学習に適した形に変換できます。
さらに、ノイズに強く、単純な弱学習器でも高い精度を発揮できるため、大規模データの分析やKaggleコンペ、実務のデータサイエンスにおいても広く活用されています。
このような特性を活かし、AdaBoostは誤分類を修正しながら学習を進める問題や、シンプルなモデルで高精度な予測を求める場面で特に効果を発揮します。

AdaBoostの仕組み

AdaBoostの構築プロセスも、基本的にGBDTと同様のブースティングの考え方に基づいていますが、誤分類されたデータに重点を置く という独自の工夫が施されています。
AdaBoostの学習ステップ
- 残差の計算:
初期モデルを作成し、各データに対して誤分類の度合いを計算します。AdaBoostでは、誤分類されたデータに重点を置きながら学習を進めるため、誤分類されたサンプルの重みを増やし、次の学習器がそれらをより正確に分類できるようにします。 - 弱学習器(決定木)の学習:
誤分類されたデータに重点を置きながら、小さな決定木(通常は深さ1のスタンプ木)を作成し、モデルに追加します。各学習器の重みを調整しながら、誤分類を修正する方向に学習を進めます。 - モデルの更新:
新しい弱学習器の予測を加えることで全体のモデルが改善され、この処理を繰り返すことで誤分類を少しずつ減らしていきます。AdaBoostは、弱学習器の組み合わせによって強力な分類器を構築し、過学習を抑えながら高精度な予測を行うことができます。
このように、AdaBoostはブースティングの原理を活かしながら、誤分類を修正しながら学習を進めることで、高精度な予測と安定した学習を両立できるように設計されています。
決定木・ランダムフォレストとの違い
| 特徴 | 決定木 | ランダムフォレスト | AdaBoost |
|---|---|---|---|
| 構造 | 1本の木 | 複数の木(並列) | 複数の弱学習器(直列) |
| 過学習のしやすさ | 高い | 低い | 低い(誤分類データに重点を置く) |
| 学習速度 | 速い | 遅い | 中程度(弱学習器の繰り返し学習) |
| 精度 | 単純なデータで高い | 複雑なデータで高い | 高い(誤分類を修正しながら学習) |
| 特徴量選択 | 全特徴量 | ランダムに一部選択 | 全特徴量(誤分類データを重視) |
| スケーラビリティ | 低い | 高い | 中程度(弱学習器の組み合わせ)) |
AdaBoostのメリット・デメリット
メリット
- 高精度な予測: 多くのケースで優れた分類性能を発揮
- 非線形な関係にも対応: 弱学習器を組み合わせることで複雑な特徴間の関係を捉える
- 特徴量の重要度を可視化: どの特徴がどれだけモデルに貢献しているかを分析可能
- 柔軟なカスタマイズ性: 弱学習器の種類、学習率、イテレーション数などを細かく調整可能
- 過学習を抑制: 誤分類データに重点を置くことで、適応的に学習を進める
デメリット
- 学習コストが高い: 弱学習器を1つずつ順番に構築するため時間がかかる
- ハイパーパラメータ調整が重要: 学習率や弱学習器の数を適切に調整しないと過学習のリスクあり
- ノイズに過敏: 特に小規模データセットでは過学習しやすい
- リアルタイム用途にはやや不向き: 推論速度はランダムフォレストより遅め
AdaBoostに適したデータ
向いているデータ
- 特徴量が多く、複雑なパターンを持つデータ
- 高精度な予測が求められる業務(金融、医療、製造業など)
- カテゴリ変数を多く含む構造化データ(数値、カテゴリデータなど)
- 回帰・分類どちらにも対応したいタスク
向いていないデータ
- リアルタイム予測が必要なシステム(学習・推論速度がネック)
- 非常に高次元・スパースなデータ(例:生のテキスト)
- ノイズの多いデータ(過学習しやすいため注意が必要)
製造業におけるAdaBoostの活用例
製造業において、AdaBoostは次の用途で使われています。
| 用途 | 概要 | タイプ | 具体例 |
|---|---|---|---|
| 異常検知 | センサーデータから異常パターンを検出し、予防保全や品質向上に貢献 | 分類 | 振動・温度・電流などの変動パターンから異常兆候を自動検出 |
| 故障予測 | 機械の状態を学習し、故障の予兆を捉える | 分類 | 異常振動の継続時間や加速度傾向をもとにベアリングの故障を予測 |
| 品質予測 | 製造条件と品質データを関連づけ、不良品の発生を抑制 | 回帰 | 温度・圧力・回転数から製品の寸法ばらつきを予測 |
| 需要予測 | 時系列データに基づき、将来の需要や在庫変動を予測 | 回帰 | 生産計画や仕入れ戦略の最適化 |
| 故障分類 | 故障発生時、その原因(電気系/機械系など)を分類 | 分類 | ログデータやセンサー値から適切な対応部門を特定 |
| 生産量最適化 | プロセス条件を調整し、最大効率の生産体制を実現 | 回帰 | 材料投入量・加工時間・気温などから最適な生産条件を推定 |
| エネルギー消費予測 | 設備や工場全体の電力使用量を予測し、省エネ施策やコスト削減に貢献 | 回帰 | 月別・時間帯別の使用傾向からピーク電力を予測し契約電力を最適化 |
AdaBoostによる分類問題の解き方
1. 事前準備(ライブラリ導入とデータ準備)
まず、以下のライブラリをインストールしてください。scikit-learn には AdaBoostClassifier が含まれているため、追加で特別なインストールは不要です。
pip install matplotlib
pip install pandas
pip install scikit-learn次に、AdaBoostの分類モデルを試すためのダミーデータを作成します。今回は、7つの特徴量から4クラスを分類するデータを使用します。製造業での応用としては、センサーによる異常検知や製品の不良予測などに置き換えることができます。
from sklearn.datasets import make_classification
import pandas as pd
# ダミーデータ作成
X, y = make_classification(
n_samples=1000,
n_features=7,
n_informative=5,
n_redundant=2,
n_classes=4,
n_clusters_per_class=1,
flip_y=0.05,
random_state=42
)
# データフレーム化
df = pd.DataFrame(X, columns=[f"特徴量_{i+1}" for i in range(7)])
df['正解データ'] = y
# ファイルに保存(任意)
df.to_csv("classification_data.csv", index=False)特徴量_1~7 は一見無秩序に見えるかもしれませんが、AdaBoostを用いることで目的変数(分類先)を高精度に予測できます。
AdaBoostを用いた分類モデルの学習と評価(サンプルコードと解説)
以下は、AdaBoostを用いて分類モデルの学習と評価を行うサンプルコードです。
このまま実行すると学習が始まり、精度評価指標(混同行列、accuracyなど)が出力されます。
学習と評価の部分は、train_adaboost_classifierという名前で関数化していますので、コピペでお使いいただけます。
import pandas as pd
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
def train_adaboost_classifier(df, target, columns, params=None, test_size=0.2, random_state=42):
"""
AdaBoostを用いた分類モデルを構築し、レポートを出力する関数。
引数:
df : pandas.DataFrame
データを含むデータフレーム。
target : str
予測対象となるターゲット列名。
columns : list of str
使用する特徴量の列名のリスト。
params : dict, optional (default=None)
AdaBoostのハイパーパラメータ。
test_size : float, optional (default=0.2)
テストデータの割合。
random_state : int, optional (default=42)
乱数シード。
戻り値:
model : AdaBoostClassifier
訓練されたAdaBoostモデルのオブジェクト。
cm : numpy.ndarray
混同行列を表す2次元配列。
"""
if params is None:
estimator = DecisionTreeClassifier(max_depth=1, random_state=random_state)
params = {
'n_estimators': 100,
'learning_rate': 0.1,
'random_state': random_state,
'estimator': estimator # sklearn 1.2以降
}
else:
if 'estimator' not in params:
params['estimator'] = DecisionTreeClassifier(max_depth=1, random_state=random_state)
columns = [col for col in columns if col != target]
X = df[columns]
y = df[target]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state)
model = AdaBoostClassifier(**params)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
report = classification_report(y_test, y_pred, target_names=[str(label) for label in sorted(y.unique())])
cm = confusion_matrix(y_test, y_pred)
print(f'正解率: {accuracy:.4f}')
print('混同行列:')
print(cm)
print('分類レポート:')
print(report)
return model, cm
if __name__ == "__main__":
df = pd.read_csv('classification_data.csv')
model, cm = train_adaboost_classifier(df, target='正解データ', columns=df.columns)正解率: 0.8600
混同行列:
[[46 1 1 3]
[ 0 44 1 1]
[ 7 0 44 2]
[10 0 2 38]]
分類レポート:
precision recall f1-score support
0 0.73 0.90 0.81 51
1 0.98 0.96 0.97 46
2 0.92 0.83 0.87 53
3 0.86 0.76 0.81 50
accuracy 0.86 200
macro avg 0.87 0.86 0.86 200
weighted avg 0.87 0.86 0.86 200
ハイパーパラメータを指定する場合は、paramsに辞書形式で指定します。必要に応じて適宜値を書き換え、実行してください。
# 関数の呼び出し(ハイパーパラメータを指定)
train_adaboost_classifier(df, target='正解データ', columns=df.columns, params={'n_estimators': 50})分類結果(混同行列)の視覚化
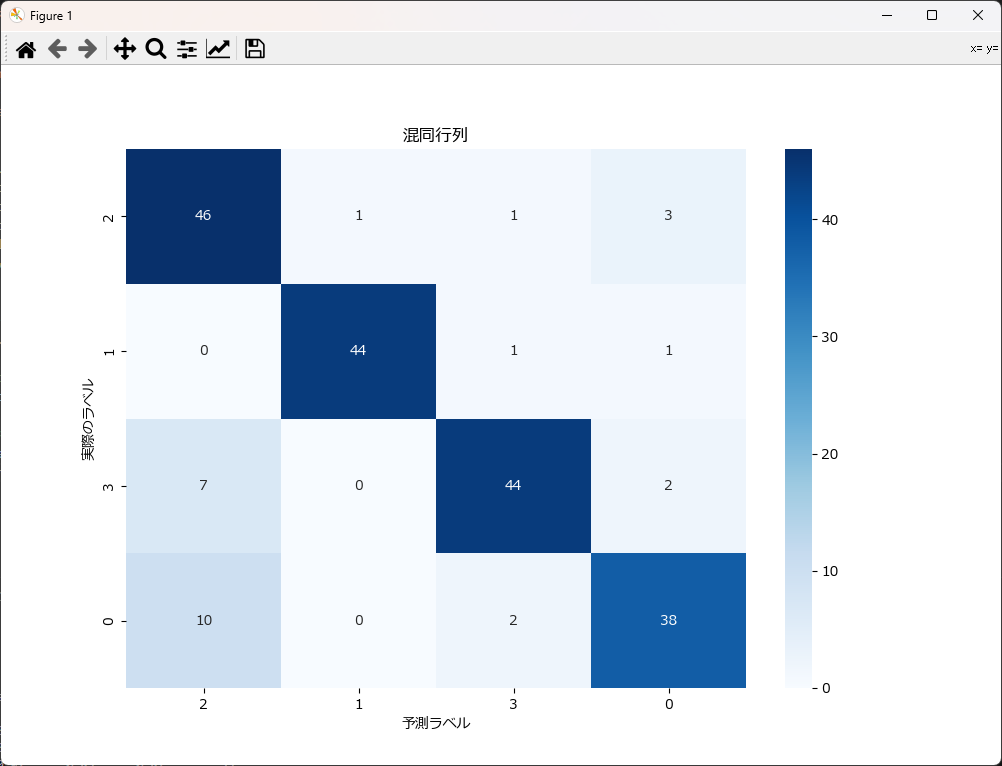
混同行列を可視化すると、結果が直感的に分かり易くなります。下記がそのサンプルです。 plot_confusion_matrixという関数名にしていますので、コピペで利用可能です。
#---------------------------------------------------------------
# この部分に、前述した train_adaboost_classifier関数 を張り付けて下さい
#---------------------------------------------------------------
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib import rcParams
import pandas as pd
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
from sklearn.preprocessing import OneHotEncoder
import numpy as np
rcParams['font.family'] = 'Meiryo'
def plot_confusion_matrix(cm, class_names=[]):
"""
混同行列をプロットする関数。
引数:
cm : numpy.ndarray
混同行列を表す2次元配列。
class_names : list of str, optional
クラス名のリスト。省略すると連番が表示される
"""
plt.figure(figsize=(10, 7))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues', xticklabels=class_names, yticklabels=class_names)
plt.xlabel('予測ラベル')
plt.ylabel('実際のラベル')
plt.title('混同行列')
plt.show()
if __name__ == "__main__":
# データを読み込む
df = pd.read_csv('classification_data.csv')
# AdaBoost分類器の学習(ハイパーパラメータはデフォルト値を使用)
model, cm = train_adaboost_classifier(df, target='正解データ', columns=df.columns)
# クラス名を設定して混同行列をプロット
class_names = df['正解データ'].unique().astype(str)
plot_confusion_matrix(cm, class_names=class_names)分類結果の評価
今回のテストデータに対してAdaBoostで分類した結果を整理し、評価してみました。
正解率
| 正解率(Accuracy) | 0.86 |
|---|
モデルの全体的な精度は非常に高いと言えます。
混同行列
| 正解の分類クラス | クラス 0の予測件数 | クラス 1の予測件数 | クラス 2の予測件数 | クラス 3の予測件数 |
|---|---|---|---|---|
| クラス 0 | 46 | 1 | 1 | 3 |
| クラス 1 | 0 | 44 | 1 | 1 |
| クラス 2 | 7 | 0 | 44 | 2 |
| クラス 3 | 10 | 0 | 2 | 38 |
クラス 0 は誤分類が 4 件、クラス 1 は誤分類が 2 件と比較的少なく、高い精度で分類されていることが確認できます。一方で、クラス 3 の誤分類が 12 件と最も多く、分類精度が低い傾向が見られます。
特に、クラス 3 のデータがクラス 0 に誤分類されるケースが多く、モデルの識別能力に課題があることが分かります。
分類レポート
| クラス | 適合率 (Precision) | 再現率 (Recall) | F1スコア (F1-Score) | サポート (Support) |
|---|---|---|---|---|
| 0 | 0.73 | 0.90 | 0.81 | 51 |
| 1 | 0.98 | 0.96 | 0.97 | 46 |
| 2 | 0.92 | 0.83 | 0.87 | 53 |
| 3 | 0.86 | 0.76 | 0.81 | 50 |
| クラス | 適合率 (Precision) | 再現率 (Recall) | F1スコア (F1-Score) | サンプル数 |
|---|---|---|---|---|
| 正解率(Accuracy) | - | - | 0.86 | 200 |
| マクロ平均 | 0.87 | 0.86 | 0.86 | 200 |
| 加重平均 | 0.87 | 0.86 | 0.86 | 200 |
この分類モデルは 全体的に高い分類性能を示しており、正解率は 0.86 となっています。
クラスごとの精度を見ると、クラス 0、クラス 1、クラス 2 は比較的安定した分類精度 を持っている一方で、クラス 3 の識別精度が若干低い ことが確認できます。
- クラス 0:
適合率 0.73、再現率 0.90 → 大部分のサンプルを正しく分類できており、再現率は高いものの、適合率が若干低め。 - クラス 1:
適合率 0.98、再現率 0.96 → 非常に高い精度で分類されており、誤予測がほとんどない。 - クラス 2:
適合率 0.92、再現率 0.83 → 正しく分類されているサンプルが多いが、他のクラスに誤分類されるケースも一定数存在するため、改善の余地がある。 - クラス 3:
適合率 0.86、再現率 0.76 → クラス 3 のデータが他のクラスと誤認されることが多く、再現率が低下している。特徴量の見直しやデータバランスの調整が必要かもしれない。 - マクロ平均(Macro Avg):
0.87(適合率), 0.86(再現率), 0.86(F1スコア) → クラスごとの精度のバランスは比較的取れているが、改善できる余地もある。 - 加重平均(Weighted Avg):
0.87(適合率), 0.86(再現率), 0.86(F1スコア) → 全体として安定した分類ができているものの、クラス 3 の改善が今後の焦点となる。
AdaBoostによる回帰問題の解き方
事前準備(ライブラリ導入とデータ準備)
事前に下記3つのライブラリをインストールしてください。scikit-learn には AdaBoostClassifier が含まれているため、追加で特別なインストールは不要です。
pip install matplotlib
pip install pandas
pip install scikit-learn
下記は今回の回帰に使うダミーデータの生成プログラムです。7つの特徴量のデータとなります。
import numpy as np
import pandas as pd
# 特徴量の数
n_features = 7
# 各特徴量の標準偏差
std_devs = [1, 1, 1, 1, 1, 1, 1]
# 相関行列の設定(例: 1番目と2番目の特徴量が強い相関を持つ)
correlation_matrix = np.array([
[1, 0.8, 0.2, 0.1, 0.1, 0.1, 0.1],
[0.8, 1, 0.3, 0.2, 0.2, 0.2, 0.2],
[0.2, 0.3, 1, 0.4, 0.3, 0.3, 0.3],
[0.1, 0.2, 0.4, 1, 0.5, 0.5, 0.5],
[0.1, 0.2, 0.3, 0.5, 1, 0.4, 0.4],
[0.1, 0.2, 0.3, 0.5, 0.4, 1, 0.3],
[0.1, 0.2, 0.3, 0.5, 0.4, 0.3, 1]
])
# 共分散行列の計算
covariance_matrix = np.outer(std_devs, std_devs) * correlation_matrix
# ダミーデータの生成
np.random.seed(42)
n_samples = 1000
data = np.random.multivariate_normal(np.zeros(n_features), covariance_matrix, size=n_samples)
# DataFrameに変換
df = pd.DataFrame(data, columns=[f'特徴量_{i+1}' for i in range(n_features)])
# 結果の確認
print(df.head())
# CSVファイルに保存
df.to_csv('regression_data.csv', index=False)下記のグラフは、分類モデル用データ生成で紹介したplot_features_with_histogramを使って描画しました。
AdaBoostによる回帰モデルの学習と評価(サンプルコードと解説)
以下は、AdaBoostを用いて回帰モデルの学習と評価を行うサンプルコードです。
実行すると学習が始まり、精度評価指標(統計情報、平均絶対誤差、平均二乗誤差、重要度など)が出力されます。
学習と評価の部分は、train_adaboost_regressorという名前で関数化していますので、コピペでお使いいただけます。
import pandas as pd
import numpy as np
from sklearn.ensemble import AdaBoostRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score, mean_absolute_percentage_error
def train_adaboost_regressor(df, target, columns, params=None, test_size=0.2, random_state=42):
"""
AdaBoostを用いた回帰モデルを学習させ、レポートを出力する関数。
引数:
df : pandas.DataFrame
データを含むデータフレーム。
target : str
予測対象となるターゲット列名。
columns : list of str
使用する特徴量の列名のリスト。
params : dict, optional (default=None)
AdaBoostのハイパーパラメータ。
test_size : float, optional (default=0.2)
テストデータの割合。
random_state : int, optional (default=42)
乱数シード。
戻り値:
model : AdaBoostRegressor
訓練されたAdaBoostモデルのオブジェクト。
y_test : list
テストに使った正解データ。
y_pred : list
予測した結果。
"""
if params is None:
estimator = DecisionTreeRegressor(max_depth=4, random_state=random_state)
params = {
'n_estimators': 100,
'learning_rate': 0.1,
'random_state': random_state,
'estimator': estimator
}
else:
# 明示的にbase_estimatorが指定されていない場合はDecisionTreeにする
if 'estimator' not in params:
params['estimator'] = DecisionTreeRegressor(max_depth=4, random_state=random_state)
columns = [col for col in columns if col != target]
X = df[columns]
y = df[target]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state)
model = AdaBoostRegressor(**params)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
mape = mean_absolute_percentage_error(y_test, y_pred)
print(f'{target}の統計情報:')
print(f'最小値(Min): {y.min()}')
print(f'最大値(Max): {y.max()}')
print(f'平均値(Mean): {y.mean()}')
print(f'標準偏差(Std): {y.std()}')
print(f'分散(Var): {y.var()}')
print('\n精度評価:')
print(f'平均絶対誤差 (MAE): {mae}')
print(f'平均二乗誤差 (MSE): {mse}')
print(f'ルート平均二乗誤差 (RMSE): {rmse}')
print(f'平均絶対パーセンテージ誤差 (MAPE): {mape}')
print(f'決定係数 (R^2): {r2}')
# 特徴量の重要度(estimatorに依存)
if hasattr(model, 'feature_importances_'):
feature_importances = model.feature_importances_
importance_df = pd.DataFrame({'特徴量 (Feature)': columns, '重要度 (Importance)': feature_importances})
importance_df = importance_df.sort_values(by='重要度 (Importance)', ascending=False)
print("\n特徴量の重要度:")
print(importance_df)
else:
print("このモデルでは特徴量の重要度を取得できません。")
return model, y_test, y_pred
if __name__ == "__main__":
df = pd.read_csv('regression_data.csv')
model, y_test, y_pred = train_adaboost_regressor(df, '特徴量_1', df.columns)
特徴量_1の統計情報:
最小値(Min): -3.4181790752853725
最大値(Max): 2.967258816333585
平均値(Mean): -0.018768452256335492
標準偏差(Std): 0.9893707041157269
分散(Var): 0.9788543901624494
精度評価:
平均絶対誤差 (MAE): 0.49020625396175277
平均二乗誤差 (MSE): 0.3865116645493002
ルート平均二乗誤差 (RMSE): 0.6217006229281906
平均絶対パーセンテージ誤差 (MAPE): 2.113389551298519
決定係数 (R^2): 0.6585815624139737
特徴量の重要度:
特徴量 (Feature) 重要度 (Importance)
0 特徴量_2 0.850308
4 特徴量_6 0.033250
1 特徴量_3 0.031746
3 特徴量_5 0.029897
5 特徴量_7 0.028892
2 特徴量_4 0.025907
回帰結果の可視化
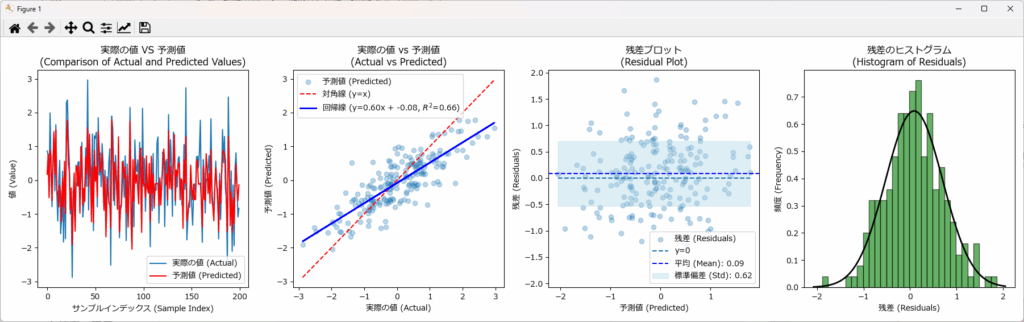
回帰結果を可視化することで、実際の値と予測値との差、残差のバラつき、残差の分布状態が直感的に把握できます。下記がそのサンプルです。 plot_figuresという関数名にしていますので、コピペで利用可能です。
#------------------------------------------------------------------------
# この部分に、前述した train_adaboost_regressor関数 を張り付けて下さい
#------------------------------------------------------------------------
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib import rcParams
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score
from scipy.stats import norm
import numpy as np
rcParams['font.family'] = 'Meiryo'
def plot_figures(y_test, y_pred):
residuals = y_test - y_pred
fig, axs = plt.subplots(1, 4, figsize=(18, 5))
axs[0].plot(y_test.values, label='実際の値 (Actual)', linestyle='-', marker=None)
axs[0].plot(y_pred, label='予測値 (Predicted)', color='red', linestyle='-', marker=None)
axs[0].set_xlabel('サンプルインデックス (Sample Index)')
axs[0].set_ylabel('値 (Value)')
axs[0].set_title('実際の値 VS 予測値\n(Comparison of Actual and Predicted Values)')
axs[0].legend()
axs[1].scatter(y_test, y_pred, alpha=0.3, label='予測値 (Predicted)')
axs[1].plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', label='対角線 (y=x)')
slope, intercept = np.polyfit(y_test, y_pred, 1)
r2 = r2_score(y_test, y_pred)
axs[1].plot(y_test, slope * y_test + intercept, color='blue', linestyle='-', linewidth=2,
label=f'回帰線 (y={slope:.2f}x + {intercept:.2f}, $R^2$={r2:.2f})')
axs[1].set_xlabel('実際の値 (Actual)')
axs[1].set_ylabel('予測値 (Predicted)')
axs[1].set_title('実際の値 vs 予測値\n(Actual vs Predicted)')
axs[1].legend()
axs[2].scatter(y_pred, residuals, alpha=0.3, label='残差 (Residuals)')
axs[2].hlines(y=0, xmin=y_pred.min(), xmax=y_pred.max(), linestyles='dashed', label='y=0')
residuals_mean = np.mean(residuals)
residuals_std = np.std(residuals)
sorted_indices = np.argsort(y_pred)
sorted_y_pred = y_pred[sorted_indices]
sorted_upper = residuals_mean + residuals_std
sorted_lower = residuals_mean - residuals_std
axs[2].axhline(y=residuals_mean, color='blue', linestyle='--', label=f'平均 (Mean): {residuals_mean:.2f}')
axs[2].fill_between(sorted_y_pred, sorted_lower, sorted_upper, color='lightblue', alpha=0.4,
label=f'標準偏差 (Std): {residuals_std:.2f}')
axs[2].set_xlabel('予測値 (Predicted)')
axs[2].set_ylabel('残差 (Residuals)')
axs[2].set_title('残差プロット\n(Residual Plot)')
axs[2].legend()
axs[3].hist(residuals, bins=30, edgecolor='k', density=True, alpha=0.6, color='g')
xmin, xmax = axs[3].get_xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, residuals_mean, residuals_std)
axs[3].plot(x, p, 'k', linewidth=2)
axs[3].set_xlabel('残差 (Residuals)')
axs[3].set_ylabel('頻度 (Frequency)')
axs[3].set_title('残差のヒストグラム\n(Histogram of Residuals)')
plt.tight_layout()
plt.show()
if __name__ == "__main__":
df = pd.read_csv('regression_data.csv')
model, y_test, y_pred = train_adaboost_regressor(df, target='特徴量_1', columns=df.columns)
plot_figures(y_test, y_pred)回帰結果の評価
精度の評価
| 指標 | 値 |
|---|---|
| 平均絶対誤差 (MAE) | 0.49020625396175277 |
| 平均二乗誤差 (MSE) | 0.3865116645493002 |
| ルート平均二乗誤差 (RMSE) | 0.6217006229281906 |
| 平均絶対パーセンテージ誤差 (MAPE) | 2.113389551298519 |
| 決定係数 (R^2 Score) | 0.6585815624139737 |
MAE、MSE、RMSE、MAPEはそれぞれ誤差の指標です。これを評価する前に、予測対象となる特徴量_1の統計情報を確認しておきましょう。
| 最小値 | 最大値 | 平均値 | 標準偏差 | 分散 |
|---|---|---|---|---|
| -3.4182 | 2.9673 | -0.01877 | 0.9894 | 0.9789 |
平均値は -0.0187 で 0 に近い ため、データの中心値はほぼ標準的な値を示しています。
標準偏差 0.989 の範囲を見ると、データの約 67% が -0.989~+0.989 の間に分布 しており、ばらつきは比較的均一です。しかし、最小値 -3.418、最大値 2.967 と 範囲が広いため、外れ値の影響を受ける可能性 があります。
また、MAE、MSE、RMSE の値を見ると、誤差は全体的に低く抑えられており、一定の予測精度が確認できます。
MAPE(2.11%)は非常に低い数値で、誤差の相対的な大きさも小さく、モデルは比較的安定した予測をしていると判断できます。
ただし、MAPE の性質上、予測対象の値が 0 に近いケースが多い場合、誤差が過小評価される可能性があるため、注意が必要です。これらの指標だけでモデルの性能を完全に判断するのは難しく、誤差の分布や外れ値の影響なども併せて評価することが重要です。
決定係数(R²スコア)は 0.659 であり、モデルの予測精度は中程度と評価できますが、さらなる改善の余地も残されています。
誤差のばらつきや MAPE の特性を考慮すると、特定のケースでは予測精度が不安定になる可能性があります。
実務への適用を前に、誤差の分布や外れ値の影響を可視化などで確認し、必要に応じてハイパーパラメータ調整や前処理を行うことで、より安定した予測モデルの構築が期待できます。
モデルの改善策
- ハイパーパラメータの調整:
learning_rateやn_estimatorsなどのパラメータを最適化し、モデルの汎化性能を向上させる。 - 特に learning_rate の調整 により、学習の安定性を確保できる。
- 特徴量の選択とエンジニアリング:
重要な特徴量を追加したり、不要な特徴量を削除することで、より精度の高い予測が可能になる。
特徴量の相関分析を行い、影響が少ない特徴量を削減するのも有効。 - データの前処理:
標準化やスケーリングを行い、データのばらつきを均一化することで モデルの性能を向上 させる。
特に外れ値の処理を適切に行うことで、過学習を防ぎ、安定した予測を実現 できる。。
可視化の結果からも、一定の予測精度が確認できる一方で、誤差の広がりや外れ値の影響が視覚的に捉えられており、さらなる改善の余地も見て取れます。

特徴量の重要度
| 特徴量 (Feature) | 重要度 (Importance) |
|---|---|
| 特徴量_2 | 0.850308 |
| 特徴量_6 | 0.033250 |
| 特徴量_3 | 0.031746 |
| 特徴量_5 | 0.029897 |
| 特徴量_7 | 0.028892 |
| 特徴量_4 | 0.025907 |
AdaBoostでは、目的変数「特徴量_1」を予測するために使用した各特徴量(特徴量_2~_7)の寄与度(重要度)を算出できます。
この結果から、特徴量_2 が圧倒的に高い重要度(0.85)を示しており、予測への主な寄与元であることが明らかです。その他の特徴量はそれぞれ 0.02~0.03 程度と比較的小さい値となっており、特徴量_2 に強く依存したモデル構造になっていると考えられます。
したがって、モデルの解釈や改善を検討する場合は、まず 特徴量_2 の内容・分布・外れ値等を詳しく分析することが重要です。
一方で、他の特徴量(_3, _4, _5, _6, _7)もわずかながら情報を提供しているため、削除する前に相関性や有効性を再評価するのが望ましいでしょう。
このように、特徴量の重要度を可視化・数値化することで、モデルの意思決定に影響を与えている要因を明確にでき、精度改善や特徴選択の判断材料として非常に有用です。
ハイパーパラメータ
予測精度を向上させるには、ハイパーパラメータの調整が重要です。AdaBoostには数多くハイパーパラメータが用意されていますが、おおよそ下記の7種類が目安となります。
n_estimators: 弱学習器の数。多いほど安定するが、計算コスト増。50~200 で調整します。
learning_rate: 学習率。高すぎると不安定、低すぎると収束が遅い。0.01~0.3 で試します。
base_estimator: 弱学習器。通常は深さ1の決定木(DecisionTreeClassifier(max_depth=1))を使用します。
algorithm: 多クラス分類時のアルゴリズム。'SAMME'(確率的重みなし) と 'SAMME.R'(確率的重みあり) の2種類があります。
max_depth: 決定木の深さ。過学習を防ぐため 1~3 で最適化。
min_samples_split: ノードを分割する最小サンプル数。汎化性能向上のため 2~10 を設定。
min_samples_leaf: 葉ノードに必要な最小サンプル数。小さいほど細かい特徴を学習可能。
AdaBoostの主要なハイパーパラメータ設定
| パラメータ名 | 説明 | 推奨値 |
|---|---|---|
| n_estimators | 弱学習器(決定木)の数。多いほど安定するが、計算コストが増加。 | 50~200 |
| learning_rate | 各決定木の影響を調整する係数。値を小さくすると汎化性能が向上しやすい。 | 0.01~0.3 |
| base_estimator | 弱学習器のモデル。通常 浅い決定木 (DecisionTreeClassifier(max_depth=1)) を使用。 | DecisionTreeClassifier(max_depth=1) |
| algorithm | 多クラス分類時のアルゴリズム。SAMME(非確率的) or SAMME.R(確率的重み付け)。 | 'SAMME.R' |
| random_state | 乱数シードを設定し、モデルの再現性を確保。 | 任意の整数 |
| max_depth | 弱学習器の決定木の深さ。過学習を防ぐため 1~3 で最適化。 | 1~3 |
| min_samples_split | ノードを分割する最小サンプル数。汎化性能向上のため 2~10 を設定。 | 2~10 |
| min_samples_leaf | 葉ノードに必要な最小サンプル数。小さいほど細かい特徴を学習可能。 | 1以上 |
| warm_start | True にすると、前回の学習結果を利用しながら追加学習が可能。 | False |
| verbose | 学習の進行状況を出力するレベル。0 は出力なし、1 は簡易出力、2 以上で詳細表示。 | 0 |
パラメータチューニング手法
ハイパーパラメータのチューニングで最もよく使われるグリッドサーチを使って、AdaBoostをチューニングする関数のサンプルです。
import pandas as pd
import numpy as np
from sklearn.ensemble import AdaBoostRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score, mean_absolute_percentage_error
def grid_search_adaboost(df, target, columns, param_grid, test_size=0.2, random_state=42):
"""
グリッドサーチを使用してAdaBoostのハイパーパラメータをチューニングし、最適なモデルを見つける関数。
引数:
df : pandas.DataFrame
データを含むデータフレーム。
target : str
予測対象となるターゲット列名。
columns : list of str
使用する特徴量の列名のリスト。ターゲットが含まれていても無視する。
param_grid : dict
グリッドサーチで試すハイパーパラメータの辞書。
test_size : float, optional (default=0.2)
テストデータの割合。
random_state : int, optional (default=42)
乱数シード。
戻り値:
best_model : AdaBoostRegressor
最適なハイパーパラメータで訓練されたAdaBoostモデルのオブジェクト。
best_params : dict
最適なハイパーパラメータの辞書。
best_score : float
グリッドサーチで得られた最適なスコア。
"""
columns = [col for col in columns if col != target]
X = df[columns]
y = df[target]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state)
estimator = DecisionTreeRegressor(max_depth=3)
model = AdaBoostRegressor(estimator=estimator, random_state=random_state)
grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=5, scoring='neg_mean_squared_error', n_jobs=-1)
grid_search.fit(X_train, y_train)
best_model = grid_search.best_estimator_
best_params = grid_search.best_params_
best_score = grid_search.best_score_
y_pred = best_model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
mape = mean_absolute_percentage_error(y_test, y_pred)
print(f'最適なハイパーパラメータ: {best_params}')
print(f'グリッドサーチの最適なスコア: {best_score}')
print(f'平均絶対誤差 (MAE): {mae}')
print(f'平均二乗誤差 (MSE): {mse}')
print(f'ルート平均二乗誤差 (RMSE): {rmse}')
print(f'平均絶対パーセンテージ誤差 (MAPE): {mape}')
print(f'決定係数 (R^2 Score): {r2}')
return best_model, best_params, best_score, y_test, y_pred
if __name__ == "__main__":
df = pd.read_csv('regression_data.csv')
param_grid = {
'n_estimators': [50, 100, 200], # iterations → n_estimators に変更
'learning_rate': [0.01, 0.1, 0.3], # 学習率
'estimator__max_depth': [1, 3, 5], # 決定木の深さ
}
best_model, best_params, best_score, y_test, y_pred = grid_search_adaboost(df, target='特徴量_1', columns=df.columns, param_grid=param_grid)グリッドサーチ後のモデルは MAPE の低下 により誤差の影響が抑えられている一方で、MAE・MSE・RMSE の増加 により予測の精度がやや悪化していることが分かります。決定係数 (R²) もわずかに低下しており、チューニングの方向性を再考し、学習率や決定木の深さを調整する必要がありそうです。
最適なハイパーパラメータ: {'estimator__max_depth': 3, 'learning_rate': 0.01, 'n_estimators': 100}
グリッドサーチの最適なスコア: -0.36956600101217274
平均絶対誤差 (MAE): 0.4972257552657448
平均二乗誤差 (MSE): 0.40066642964193766
ルート平均二乗誤差 (RMSE): 0.6329821716619969
平均絶対パーセンテージ誤差 (MAPE): 1.8652461649824397
決定係数 (R^2 Score): 0.6460781938857283
AdaBoostが簡単に使える自作クラス
AdaBoostで分類と回帰のモデルを簡単に作成できるように、必要な機能をまとめたクラスを作りました。
下記に詳しい説明とソースコードを掲載しています。
コピペで使えるようになっていますので、是非ご活用下さい。
【コピペOK】ランダムフォレストやLightGBMを簡単に扱える自作クラスを紹介

まとめ
AdaBoost(Adaptive Boosting) は、弱学習器を組み合わせて強力なモデルを構築する機械学習アルゴリズムです。
特に 誤分類されたデータに重点を置いて学習を進める 仕組みを採用しており、単純な決定木(スタンプ木)を多数組み合わせることで高精度な予測を可能にします。
本記事では、AdaBoostの基本的な仕組みやメリット・デメリットを解説 し、製造業での活用例や具体的な実装方法について紹介しました。
また、分類や回帰における評価指標や特徴量の重要度解析、さらには効率的なハイパーパラメータチューニングの手法 も取り上げました。
これらを活用することで、実務においてAdaBoostを最適な形で導入し、高精度なモデルを構築することが可能になります。
本記事が、皆さんのプロジェクトにおいてAdaBoostの導入や活用のヒント になれば幸いです。









コメント