製造業や品質管理の現場では、「いつ機械が故障するのか?」を予測することが重要です。その答えを導くために活用されるのがワイブル分布。これは、スマートフォンのバッテリー寿命や自動車部品の耐久性など、時間の経過に伴う故障の「ばらつき」を数学的に表現できる確率分布の一種です。
本記事では、ワイブル分布の基本を分かりやすく解説し、Pythonを使った故障予知の実践方法を紹介します。コピペで使えるサンプルコードも掲載しているので、データ分析初心者でもすぐに試せます。故障予知を実践したい方はぜひご覧ください。
ワイブル分布とは
統計学の分野で特に信頼性工学や材料科学において広く利用される「ワイブル分布」は、製品の寿命や材料の強度といった、時間や応力に伴って劣化する現象を、確率分布として統計的に表現したものです。
ワイブル分布は、スウェーデンの数学者ワロッディ・ワイブル(Waloddi Weibull, 1887-1979)によって考案されました。彼は、「最弱リンクモデル」に基づき、材料や製品が一番弱い部分から壊れる現象を統計的に表現しようとしました。この理論は1951年の論文「A Statistical Distribution Function of Wide Applicability」によって広く知られるようになり、現在では製品の信頼性評価や品質管理に欠かせないツールとして多くの分野で活用されています。
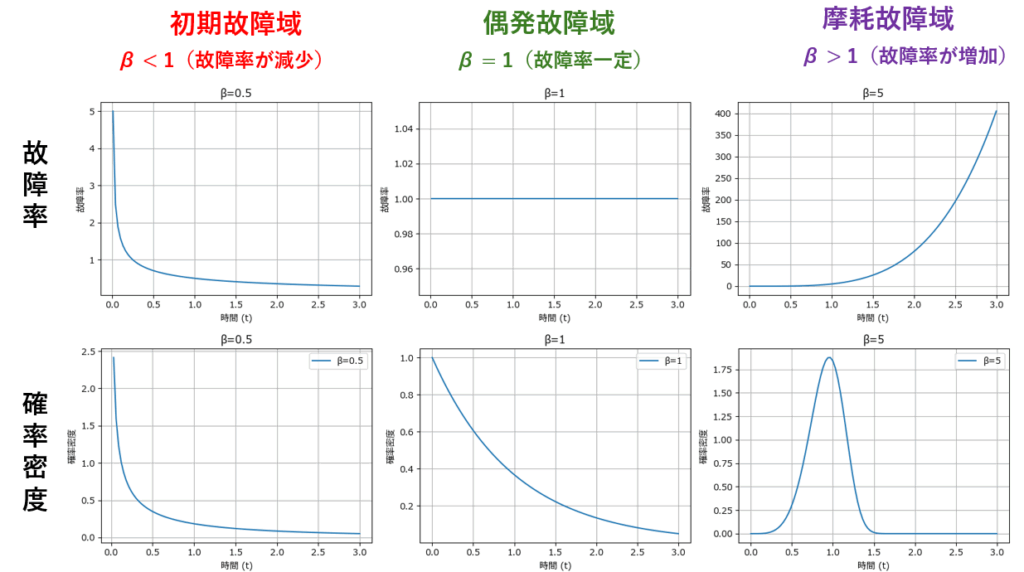
ワイブル分布は、βとη(エータ)という2つのパラメータで形が変わるのが特徴です。βは分布の形状を現わしており、0.1~5まで変化させることで、次のように分布が変形します。

一方、ηは変化の緩やかさを現わすパラメータです。分かり易いようにβ=1を固定にし、ηを0.1~5まで変化させると、次のように時間軸の幅が変化します。
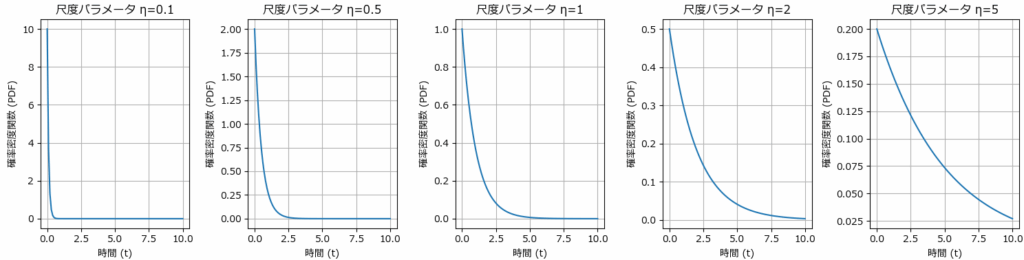
パーツや製品を使い始めてから故障するまでの時間をプロットすることで、故障の確率分布がグラフ化できます。このグラフの形状からワイブル分布であることを確認できれば、ワイブル分布の計算式を用いた故障予測が可能になります。
β(形状母数)は、値が大きいほど「寿命にばらつきが少ない」傾向があり、製品の品質が安定しているとも言えます。これは、分布が尖って集中し、故障時期が似通ってくるため、寿命のばらつきが小さくなるためで、故障時期が予測しやすくなります。
η(尺度母数)は、63.2%が故障する時間(または寿命)を現わしています。正確には「時間が η のとき、累積故障率(生存関数)が約63.2%になる」という意味になります。η は中央値や平均寿命(MTTF)とは異なる点は押さえておきたいポイントです。
故障予知の原理
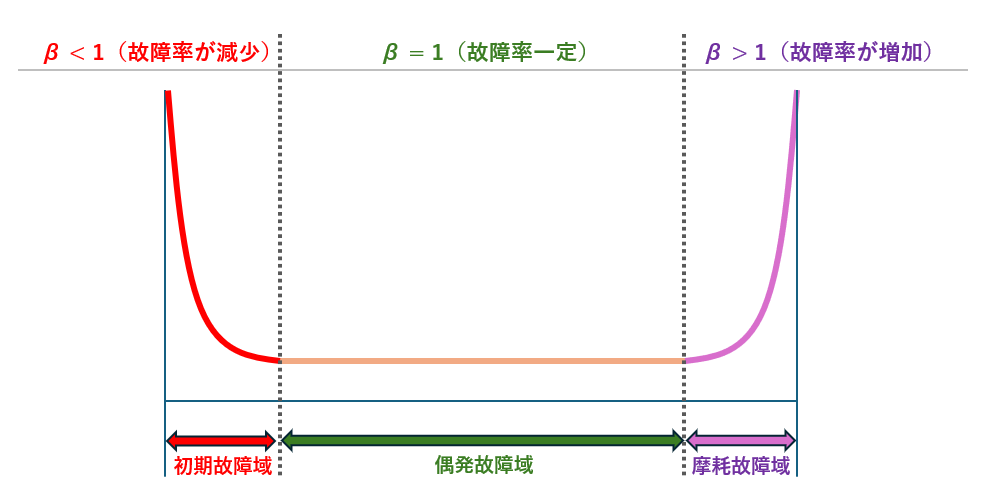
製品が稼働し始めてから寿命を迎えるまでの故障率の変化をグラフで表すと、上図の様な「バスタブ曲線」になります。この曲線は、故障率の変化に応じて3つの部位(初期故障域、偶発故障域、摩耗故障域)に分割することができます。
| 故障域 | β値 | 変化 | 説明 |
|---|---|---|---|
| 初期故障域 | β < 1 | 減少 | 製品が稼働し始めた直後の期間。初期の不具合が多く発生し、時間の経過とともに故障率が低下する。 |
| 偶発故障域 | β = 1 | 一定 | 製品が安定して稼働する期間。偶発的な故障はあるものの、故障率は一定に保たれる。 |
| 摩耗故障域 | β > 1 | 増加 | 製品の寿命が近づくにつれて故障率が上昇。摩耗や劣化による故障が増加する。 |
もし、あるパーツの故障発生確率がワイブル分布であった場合、新たに使い始めたパーツの使用時間から、現時点の故障率(瞬間的な故障率)を求めたり、βやηを推定することにより、市場に投入してからどれくらい経過すると、どれくらい故障が発生するか(指定区間内の故障確率)を知ることができまます。
ワイブル分布の故障率関数
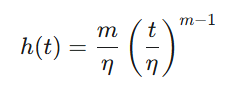
ワイブル分布の確率密度関数 (PDF)
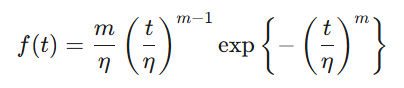
ワイブル分布の活用
信頼度関数(生存関数)の算出と信頼性予測
- 故障率や確率密度だけでなく、「ある時刻 t までに故障しない確率」、すなわち信頼度 R(t) を算出することが、ワイブル分布の主要な利用目的の一つです。これは、製品が指定された期間にわたって正常に機能し続ける確率を示し、製品保証期間の設定や、特定の期間における信頼性の目標達成度を評価する上で不可欠です。
- 計算式としては、R(t)=exp[−(t/η)β] で表されます。この信頼度関数を用いることで、「1000時間稼働した場合、何%の製品が故障せずに残っているか」といった、より直接的な信頼性評価が可能になります。
累積故障確率(不信頼度関数)の算出と故障発生数の予測
- 信頼度と表裏一体ですが、「ある時刻 t までに故障する確率」である累積故障確率 F(t)(不信頼度関数とも呼ばれる) を求めることも非常に重要です。F(t)=1−R(t) で計算されます。
- これにより、「指定された期間内に何台の製品が故障する見込みか」といった、具体的な故障台数の予測が可能になります。これは、部品の在庫計画、修理体制の構築、保証費用の見積もりなどに直結します。
特性寿命 (η) と平均寿命(MTTF/MTBF)の推定
- ワイブル分布の尺度パラメータ η は特性寿命と呼ばれ、累積故障確率が約63.2%となる時間を示します。これは、データの分布の中央付近を示す重要な指標です。
- また、ワイブル分布のパラメータを用いて、製品の平均寿命 (Mean Time To Failure: MTTF / Mean Time Between Failures: MTBF) を推定することができます。これは、特に偶発故障が支配的な期間において、製品の平均的な稼働時間を把握する上で非常に有用です。
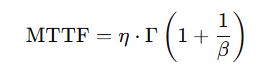
加速寿命試験データの解析
- 製品の寿命が非常に長く、通常の試験では故障データが十分に得られない場合、高温、高湿度、高負荷などの加速条件下で試験を行い、短時間で故障を発生させることがあります(加速寿命試験)。
- ワイブル分布は、この加速寿命試験で得られたデータを解析し、正規の使用条件下での寿命を推定するために広く用いられます。これにより、新製品の開発期間短縮や、信頼性評価の効率化が図れます。
残存寿命予測(Remaining Useful Life - RUL)
- 稼働中の個々の製品が、あとどれくらいの期間故障せずに稼働し続けるか(残存寿命)を予測するためにワイブル分布が利用されることがあります。これは、予知保全(Predictive Maintenance)の分野で特に重要であり、設備管理の最適化に貢献します。
信頼性保証期間の設定と費用分析
- 製品の信頼度に基づいて、最適な保証期間を設定することができます。ワイブル分布による故障予測は、保証期間中に発生するであろう故障の総数や、それに伴う保証費用の見積もりを行う上で不可欠なツールとなります。
ワイブル分布のメリットとデメリット
ワイブル分布のメリット
- 汎用性が高い(多様な故障モードに対応可能)
形状パラメータ β の値を変えることで、初期故障(β<1)、偶発故障(β=1、指数分布に相当)、摩耗故障(β>1)という異なる故障モードを単一の分布で表現できる点が最大のメリットです。これにより、製品のライフサイクル全体にわたる故障挙動を分析できます。
また、ベアリングの疲労寿命、半導体の電気的故障、材料の強度、さらには人間工学における反応時間など、非常に広範な現象のモデリングに適用できます。 - 少ないデータでも解析が可能
特に加速寿命試験や、まだ故障が少ない製品の初期段階において、限られた故障データや、未故障のデータ(打ち切りデータ)からでも、比較的正確にパラメータを推定できる手法が確立されています。これにより、開発段階や市場投入初期でも信頼性予測を行うことが可能です。 - パラメータの物理的意味付けが可能
形状パラメータ β は故障モード(故障率の変化傾向)を示し、尺度パラメータ η は特性寿命(製品の寿命の目安)を示すため、これらのパラメータから物理的な洞察を得やすいです。これは、製品設計の改善や信頼性向上に役立つ情報となります。 - 累積故障確率や信頼度関数の算出が容易
計算式が比較的シンプルであり、信頼度関数や累積故障確率などを直接的に求めることができるため、将来の故障率、残存率、保証期間内の故障台数などを予測し、信頼性管理に活用しやすいです。 - グラフィカルな解析が容易(ワイブル確率紙)
ワイブル確率紙という特殊なグラフ用紙を用いることで、故障データをプロットするだけで、データがワイブル分布に従うかどうかの確認や、パラメータの概算を視覚的に行うことができます。これは直感的で分かりやすい解析手法です。
ワイブル分布のデメリット
- パラメータ推定の複雑さ:
特に精度を求める場合、最尤法などの統計的手法を用いたパラメータ推定が必要となり、手計算では複雑になることがあります。専用のソフトウェアや統計ツールが必要となる場合が多いです。
また、データ数が極端に少ない場合や、データのばらつきが大きい場合、推定されたパラメータの信頼性が低くなる可能性があります。 - 適切なモデル選択の重要性
ワイブル分布は非常に汎用性が高いですが、全ての現象に万能というわけではありません。例えば、特定の物理的メカニズムによってガウス分布(正規分布)や対数正規分布に従うべき現象に無理にワイブル分布を適用すると、誤った結論を導く可能性があります。
3パラメータワイブル分布(位置パラメータ γ を含む)を考慮する場合、パラメータが増えることでモデルの複雑さが増し、推定がさらに難しくなることがあります。 - 外れ値への影響
データ中に極端な外れ値が存在する場合、パラメータの推定結果が大きく影響を受け、モデルの精度が低下する可能性があります。適切なデータ前処理や外れ値の考慮が必要です。 - 物理的根拠の曖昧さ
数学的に多くの現象にフィットするというメリットがある反面、特定の故障メカニズムに対する物理的な根拠が他の分布(例:正規分布がランダムな誤差の積み重ねを示すように)ほど明確でない場合もあります。これは、統計的な適合度は高くても、その背後にある物理現象の解明には別の分析が必要な場合があることを意味します。
製造業での活用事例
| 活用領域 | 事例例 | 内容・手法 | 主な活用ポイント |
|---|---|---|---|
| 製品寿命の予測と保証期間の設定 | ・冷蔵庫、洗濯機・自動車部品(エンジン等)・電子部品(IC等)・産業機械(ポンプ等) | 故障データを収集し、ワイブル分布で解析。形状パラメータβ、尺度パラメータηを推定。 | ・故障率の時間的推移を予測し、品質管理に活用・信頼度(R(t))から信頼性を数値化・保証期間内の故障数予測による保証最適化 |
| 部品の選定とサプライヤー評価 | ・電子部品の比較試験・機械部品の耐久性評価 | 複数サプライヤーから部品を調達し、加速寿命試験で故障データを取得。寿命特性をワイブル分布で比較。 | ・長寿命な部品の選定による製品信頼性向上・信頼性を指標としたサプライヤー評価 |
| 予知保全とメンテナンス計画 | ・ロボットアーム・CNCマシン・航空機エンジン部品・鉄道車両の車輪 | 故障履歴を基にワイブル分布で部品ごとの寿命特性(β、η)を推定。 | ・摩耗故障(β>1)に対して最適な交換時期を予測・在庫量の最適化・メンテナンス費用の削減 |
| 品質改善と設計変更の効果検証 | ・初期不良の低減施策・製造プロセス変更後の評価 | 設計・工程変更の前後で故障データを比較し、β・ηの変化を確認。 | ・βの増加→初期故障の抑制評価・ηの増加→寿命の延長効果を確認 |
| 顧客クレーム分析とリスク管理 | ・製品回収の判断材料・故障報告傾向の分析 | クレーム発生時刻のデータをワイブル分布で解析し、リコール判断やクレーム集中時期の有無を調査。 | ・信頼性問題の早期発見・重大な安全リスクの把握と対応策立案 |
ワイブル分布の適合評価
打ち切り時間と打ち切りデータについて
データがワイブル分布に従うかを検証する際に重要なポイントとして、打ち切り時間と打ち切りデータがあります。
ワイブル分布の検証においては、あるパーツや製品が使われ始めてからイベント(故障や評価期間の終了など)が発生するまでの時間をプロットします。
この際、データ収集の制約や評価期間の都合により、全てのパーツや製品が故障するまで観察を続けることができない場合があります。例えば、あらかじめ設定した観察期間の上限まで故障しなかったパーツや製品、または故障以外の理由で観察が終了したパーツや製品などです。
これらの、「イベントが観察期間内に発生しなかった」ことを示す時間情報を「打ち切り時間」と呼び、「打ち切り時間」内に故障しなかったデータを「打ち切りデータ」と呼びます。
打ち切りデータは、「その時間までは故障しなかった」という貴重な情報を含んでおり、ワイブル分布のパラメータを正確に推定し、より信頼性の高い故障予知を行うために不可欠です。
「打ち切り時間」は、パーツや製品のリリース日を起点に、現時点までの期間を設定することが多いです。例えば、10年前にリリースされた製品Aの場合、打ち切り時間は10年間×365日×24時間=87,600時間になります。
「打ち切り時間」は、故障しなかったものに分類するための上限値であるため、場合によっては走行時間や走行距離、サイクルや枚数、個数など、目的に応じて様々な指標を使います。
下記は、以降の説明に使うサンプルデータの生成プログラムです。
import numpy as np
import pandas as pd
# --- サンプルデータの生成設定 ---
np.random.seed(42) # 再現性のためのシード設定
# ワイブル分布の真のパラメータを設定 (ここでは摩耗故障傾向のデータを想定)
true_beta = 3.0 # 形状パラメータ (β) - 摩耗故障傾向 (>1)
true_eta = 1000 # 尺度パラメータ (η) - 特性寿命
num_samples = 100 # 生成するデータ数
# ワイブル分布から故障時間を生成
# 注意: np.random.weibull は尺度パラメータを1としているため、
# 生成後に true_eta を掛けてスケールを調整します。
raw_failure_times = np.random.weibull(true_beta, size=num_samples) * true_eta
# 打ち切りデータを導入 (ここでは、1200時間で試験を終了すると仮定)
# 1200時間を超えて故障したものは、1200時間で打ち切りとする
observed_times = np.where(raw_failure_times > 1200, 1200, raw_failure_times)
# 故障したかどうかを示すフラグ
# observed_times == raw_failure_times の場合、実際に故障した(イベント発生)
# それ以外は打ち切り(イベント未発生)
event_observed = (observed_times == raw_failure_times)
# データフレームの作成
df_sample_data = pd.DataFrame({
'ID': range(1, num_samples + 1), # 製品ID
'Time': observed_times, # 観察された時間(故障時間または打ち切り時間)
'Event': event_observed # 故障したかどうか (True=故障, False=打ち切り)
})
# CSVファイルとして保存
csv_filename = 'weibull_sample_data.csv'
df_sample_data.to_csv(csv_filename, index=False)
print(f"サンプルデータを '{csv_filename}' に保存しました。")
print("\n生成されたデータの最初の5行:")
print(df_sample_data.head())
print("\n故障データの数:", df_sample_data['Event'].sum())
print("打ち切りデータの数:", (~df_sample_data['Event']).sum())生成されるデータは次の通りです。Timeが経過時間で、Eventが故障発生の有無を現わします。サンプルデータの打ち切り時間が1200なので、1200時間経過しても故障が発生しなかったデータ(1200.0,False)も、ところどころに混ざっています。
ID,Time,Event
1,777.0942124066257,True
2,1200.0,False
3,1096.0590918047678,True
4,970.0954856141816,True
~~~以下省略~~~
ワイブル確立プロットによる分布の適合評価
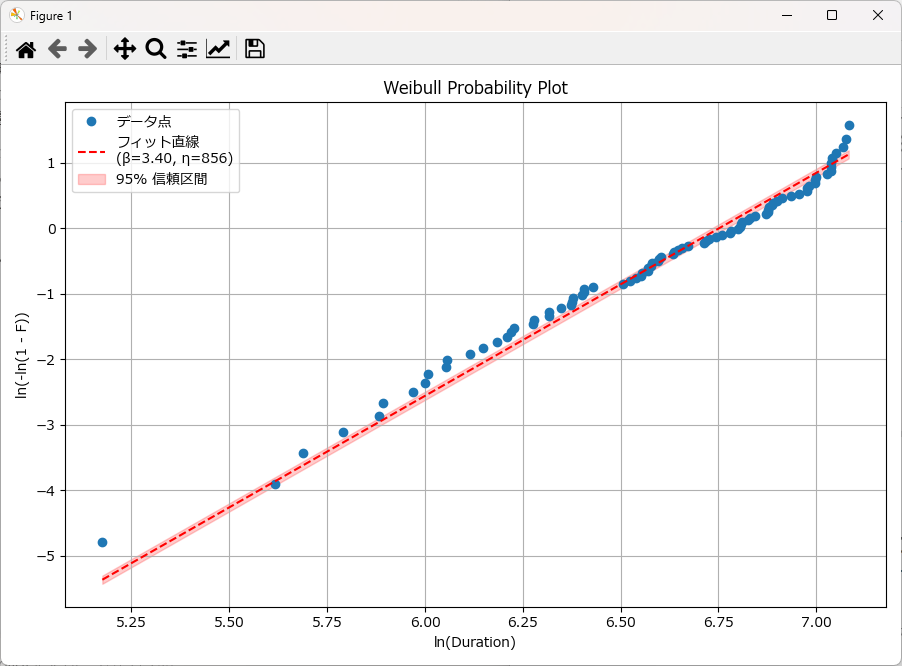
データがワイブル分布に従っているかを確認する方法として、よく使われる方法がワイブル確立プロット(Weibull Probability Plot)です。
横軸(x軸)には故障時間や寿命データを、縦軸(y軸)には対数変換された累積故障確率(累積分布関数)を設定し、データをプロットします。データがワイブル分布に従う場合、プロット上でほぼ直線的に分布します。
累積故障確率 = ln(-ln(1 - F))
下記は、先ほど生成したサンプルデータを使って、ワイブル確立プロットを描画するサンプルプログラムです。
サンプルデータを格納したDataFrame、duration_col(今回はTime列)、イベント列(今回は Event)を引数に指定することで、簡単に描画できます。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import weibull_min
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
def plot_weibull_probability(df, duration_col, event_col, confidence=0.95):
"""
Weibull確率プロットを描画する関数(理論線・信頼区間付き)
Parameters:
- df: pandas.DataFrame
データフレーム(寿命データ or 任意の観測値)
- duration_col: str
寿命または観測値の列名
- event_col: str
イベントが発生したかどうか(True/False)の列名
- confidence: float
信頼区間の信頼水準(例: 0.95)
Returns:
- なし(グラフを表示)
"""
# 故障 or イベント発生のみ取り出し
data = df[df[event_col]][duration_col].values
data_sorted = np.sort(data)
n = len(data_sorted)
# 経験的累積分布(Bernardの公式)
F = np.array([(i - 0.3) / (n + 0.4) for i in range(1, n + 1)])
ln_time = np.log(data_sorted)
ln_ln_y = np.log(-np.log(1 - F))
# ワイブル分布フィッティング。flocは位置パラメータ。
# 多くの寿命データはゼロからスタートする(負にならない)ので、floc=0を指定するのが通例。
shape, loc, scale = weibull_min.fit(data, floc=0)
# 理論線と信頼区間の描画準備
x_theory = np.linspace(data_sorted.min(), data_sorted.max(), 100)
ln_x_theory = np.log(x_theory)
F_theory = weibull_min.cdf(x_theory, shape, loc=0, scale=scale)
ln_ln_F_theory = np.log(-np.log(1 - F_theory))
# 信頼区間(正規近似)
z = abs(np.percentile(np.random.normal(0, 1, 100000), [(1 - confidence) / 2 * 100, (1 + confidence) / 2 * 100]))
stderr = 1 / (shape * np.sqrt(n))
ln_ln_F_upper = ln_ln_F_theory + z[1] * stderr
ln_ln_F_lower = ln_ln_F_theory - z[1] * stderr
# プロット
plt.figure(figsize=(9, 6))
plt.plot(ln_time, ln_ln_y, 'o', label='データ点')
plt.plot(ln_x_theory, ln_ln_F_theory, 'r--', label=f'フィット直線\n(β={shape:.2f}, η={scale:.0f})')
plt.fill_between(ln_x_theory, ln_ln_F_lower, ln_ln_F_upper, color='r', alpha=0.2, label=f'{int(confidence*100)}% 信頼区間')
plt.xlabel('ln(Duration)')
plt.ylabel('ln(-ln(1 - F))')
plt.title('Weibull Probability Plot')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
# --- 使用例 ---
if __name__ == "__main__":
# データの読込
csv_filename = 'weibull_sample_data.csv'
df = pd.read_csv(csv_filename)
# ワイブル確率プロット
plot_weibull_probability(df, duration_col='Time', event_col='Event')結果は以下の通りです。サンプルデータだけあって、ほぼ直線状に並んでいますね。
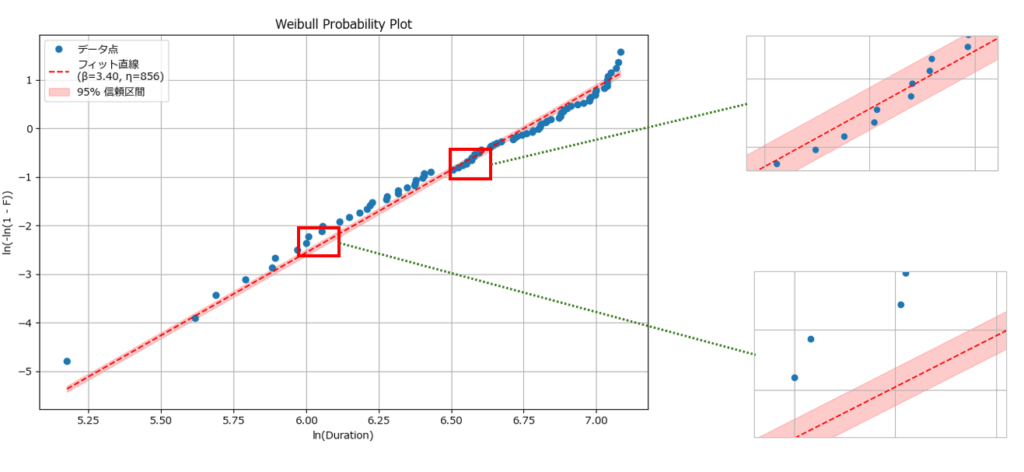
青い点(データ点)が赤い直線(理論線)に沿って並んでいるので、Weibull分布で非常によく説明できていることが分かります。
特に中央~右側(ln(Duration) が大きい領域)では密に直線上にあるため、中高寿命帯での予測に信頼性があると解釈できます。
ヒストグラム +確率密度関数を用いた分布の適合評価
ヒストグラム と確率密度関数(PDF) を重ね合わせることで、ワイブル分布か否かを確認する方法もよく用いられます。
- データからヒストグラムを描く(密度表示にするため
density=Trueを使う)。 scipy.stats.weibull_min.fit()でパラメータ(βとη)を推定。- 上記パラメータに基づいて 理論分布(PDF)を計算。
- そのPDFをヒストグラムに 重ねてプロット。
下記は、ヒストグラム + PDF フィッティングを描画するサンプルプログラムです。サンプルデータを格納したDataFrame、duration_col(今回はTime列)、イベント列(今回は Event)を引数に指定することで、簡単に描画できます。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import weibull_min
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
def analyze_weibull_distribution(df, duration_col, event_col):
"""
データフレーム df の故障時間と故障イベントを使用して、ワイブル分布を推定し、ヒストグラムと比較する
Parameters:
df : pandas.DataFrame
ワイブル分析を行うデータフレーム
duration_col : str
故障時間のカラム名
event_col : str
故障イベント(True/False)のカラム名
"""
# 故障イベントが発生したデータのみ抽出
failure_times = df[df[event_col]][duration_col].values
# ワイブル分布のパラメータを推定(形状パラメータ β、尺度パラメータ η)
shape, loc, scale = weibull_min.fit(failure_times, floc=0)
print(f"推定された形状パラメータ β: {shape:.3f}")
print(f"推定された尺度パラメータ η: {scale:.3f}")
# ヒストグラム+フィットしたワイブル分布の描画
x = np.linspace(0, failure_times.max(), 100)
pdf_fitted = weibull_min.pdf(x, shape, loc=loc, scale=scale)
plt.hist(failure_times, bins=15, density=True, alpha=0.6, label='実データ')
plt.plot(x, pdf_fitted, 'r-', label='フィットしたワイブル分布')
plt.xlabel(duration_col)
plt.ylabel('Density')
plt.title('ヒストグラムとフィットしたワイブル分布')
plt.legend()
plt.grid(True)
plt.show()
# --- 使用例 ---
if __name__ == "__main__":
# データフレームを作成(実際はCSVを読み込む)
csv_filename = 'weibull_sample_data.csv'
df = pd.read_csv(csv_filename)
# ヒストグラム + PDF の描画
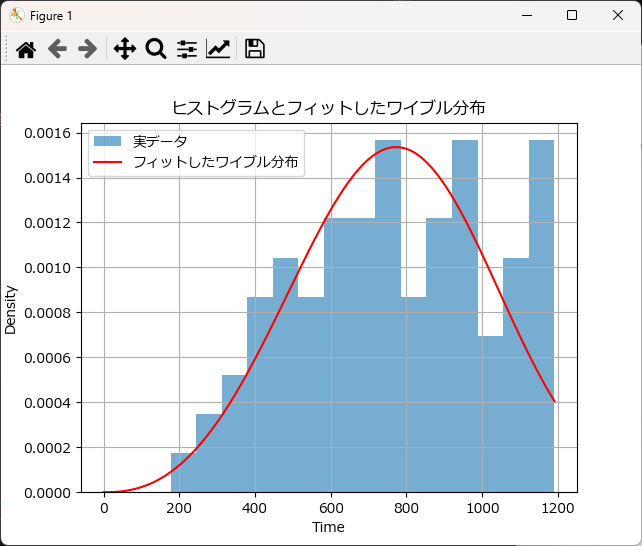
analyze_weibull_distribution(df, duration_col='Time', event_col='Event')実行すると、推定されたβとηがコンソールに出力されます。
推定された形状パラメータ β: 3.405
推定された尺度パラメータ η: 855.996
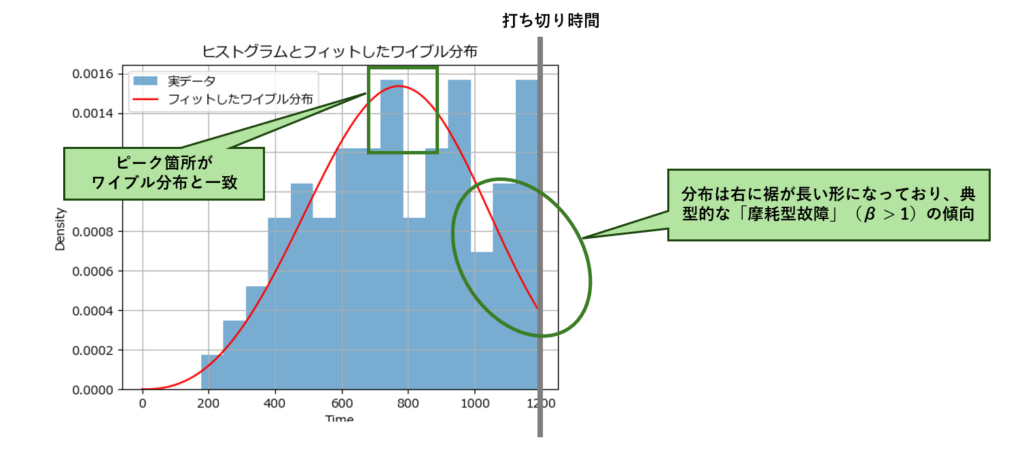
赤い理論曲線は、青いヒストグラムに対して 概ね良好にフィットしているように見えます。特に分布の中心付近(700~900)でピークが合っており、データがワイブル分布に従っている可能性が高いことを示唆しています。
また、分布は右に裾が長い形になっており、典型的な「摩耗型故障」(β > 1)の傾向が見られます。
以上のことから、おおむねワイブル分布に従っており、フィッティングは良好だと判定できます。
βとηから中央値と平均寿命を求める
ワイブル分布では、形状母数 β と尺度母数 η が分かれば、故障時間の中央値(50%が故障する時間)や、平均寿命(MTTF)を理論的に求めることができます。
| 項目名 | 意味 | 計算式 |
|---|---|---|
| 中央値 | 生存確率が0.5になる時間(50%が故障する時間)。 | |
| MTTF | 期待値(平均的な寿命)であり、βによって中央値より大きくなったり小さくなったりする。 |
import numpy as np
import pandas as pd
from scipy.stats import weibull_min
from scipy.special import gamma # ガンマ関数
def calculate_weibull_parameters(df: pd.DataFrame, duration_col: str, event_col: str) -> dict:
"""
DataFrameからワイブル分布の形状パラメータβ、尺度パラメータη、中央値、MTTFを推定。
Parameters:
- df: pandas.DataFrame
- duration_col: 寿命や経過時間を表す列名
- event_col: 故障イベント(True/False)を表す列名
Returns:
- dict: {'beta': β, 'eta': η, 'median': 中央値, 'mttf': 平均寿命}
"""
# 故障したデータ(Event=True)のみを使用
failure_data = df[df[event_col] == True][duration_col]
# ワイブル分布にフィット
beta, loc, eta = weibull_min.fit(failure_data, floc=0)
# 中央値: η * (ln(2))^(1/β)
median = eta * (np.log(2)) ** (1 / beta)
# MTTF(平均寿命): η * Γ(1 + 1/β)
mttf = eta * gamma(1 + 1 / beta)
return {
'beta': beta,
'eta': eta,
'median': median,
'mttf': mttf
}
# --- 使用例 ---
if __name__ == "__main__":
# データフレームを作成(実際はCSVを読み込む)
csv_filename = 'weibull_sample_data.csv'
df = pd.read_csv(csv_filename)
#
result = calculate_weibull_parameters(df, duration_col='Time', event_col='Event')
print(f"形状パラメータ β : {result['beta']:.3f}")
print(f"尺度パラメータ η : {result['eta']:.3f}")
print(f"中央値(50%が故障) : {result['median']:.3f}")
print(f"平均寿命(MTTF) : {result['mttf']:.3f}")形状パラメータ β : 3.405
尺度パラメータ η : 855.996
中央値(50%が故障) : 768.642
平均寿命(MTTF) : 769.070
ワイブル分布を使った故障予知(予測保全)
故障予知(予測保全)は、機器や部品の故障を事前に検知し、メンテナンス計画に役立てることが目的です。たとえば、すでに500時間使用された部品に対し、次の200時間でどの程度の確率で故障するかを求めることで、計画的な交換や保全スケジュールの最適化が可能になります。
故障予知では、 故障率(時間あたりの故障リスク)を使って評価しますが、データから推定されたβ と ηを使うことで、故障率が簡単に算出できます。
下記のサンプルプログラムは、現在までの使用時間と、次の使用時間を指定することで、その間に故障する確率を求めるものです。
import pandas as pd
import numpy as np
from lifelines import WeibullFitter
def weibull_failure_probability(df, time_start, time_end):
"""
Weibullモデルを使用して、特定の時間範囲での故障確率を計算する関数
:param df: データフレーム (Time列とEvent列を含む)
:param time_start: 計算開始時間
:param time_end: 計算終了時間
:return: 故障確率(%表記)
"""
# Weibullモデルのフィッティング
wf = WeibullFitter()
wf.fit(durations=df['Time'], event_observed=df['Event'])
# 推定されたパラメータの表示
print("推定された形状パラメータ β:", round(wf.rho_, 3))
print("推定された尺度パラメータ η:", round(wf.lambda_, 3))
# 生存関数を用いた故障確率の計算
S_start = wf.survival_function_at_times(time_start).values[0]
S_end = wf.survival_function_at_times(time_end).values[0]
failure_prob = S_start - S_end
return f"部品が {time_start}~{time_end} 時間の間に故障する確率: {failure_prob:.2%}"
if __name__ == "__main__":
# CSVデータの読み込み
df = pd.read_csv('weibull_sample_data.csv')
# 例: 500時間~700時間の間に故障する確率を計算
result = weibull_failure_probability(df, 500, 700)
print(result)推定された形状パラメータ β: 2.863
推定された尺度パラメータ η: 965.023
部品が 500~700 時間の間に故障する確率: 18.77%
ワイブル分布を使った信頼性確認(製品評価)
信頼性確認とは、製品や部品の寿命傾向や品質のばらつきを評価し、安全性や性能を保証するための作業です。
特に、長期間使用される製品では、故障の発生確率や耐久性を正確に把握することが求められます。
信頼性確認の指標として、信頼度(故障しない確率)や 故障率(時間あたりの故障発生の強さ)が使われます。
データから推定されたβとηを使って、この信頼度と故障率を求めることができます。
| 信頼度(Reliability Function) | 製品が 時刻 t を超えて故障せずに生き残る確率。 |
|---|---|
| 故障率(Hazard Function) | 時刻 t に「まだ故障していない」条件のもとで、「すぐに故障するリスク」。 |
import pandas as pd
import numpy as np
from lifelines import WeibullFitter
def evaluate_reliability(df, t):
"""
Weibullモデルを使用して、指定時刻での信頼性評価を行う関数
:param df: データフレーム (Time列とEvent列を含む)
:param t: 評価したい時刻(時間)
:return: 信頼度(生存関数)と故障率(ハザード関数)
"""
# Weibullモデルのフィッティング
wf = WeibullFitter()
wf.fit(durations=df['Time'], event_observed=df['Event'])
# 信頼度(生存関数): R(t) = P(T > t)
reliability = wf.survival_function_at_times(float(t)).values[0]
# 故障率(ハザード関数): h(t) = f(t) / R(t)
try:
hazard_rate = wf.hazard_at_times(float(t)).values[0]
except KeyError:
hazard_rate = np.nan # t が範囲外なら NaN を返す
# 結果の出力
print(f"形状パラメータ β: {wf.rho_:.3f}")
print(f"尺度パラメータ η: {wf.lambda_:.3f}")
print(f"信頼度 R({t})(t時間まで故障しない確率): {reliability:.2%}")
if np.isnan(hazard_rate):
print(f"故障率 h({t})(t時間時点での故障の激しさ): データ範囲外")
else:
print(f"故障率 h({t})(t時間時点での故障の激しさ): {hazard_rate:.6f} / 時間")
if __name__ == "__main__":
# CSVデータの読み込み
df = pd.read_csv('weibull_sample_data.csv')
# 評価する時刻(例: 800時間)
evaluate_reliability(df, 800)形状パラメータ β: 2.863
尺度パラメータ η: 965.023
信頼度 R(800)(t時間まで故障しない確率): 55.74%
故障率 h(800)(t時間時点での故障の激しさ): 0.002092 / 時間
まとめ
本記事では、ワイブル分布の概要と、データがワイブル分布であることの確認方法、データから推定したβとηを活用した故障予知と信頼性確認について解説しました。
ワイブル確率プロットやヒストグラムを用いることで、データの分布を視覚的に評価し、モデルの適合度を確認できました。また、形状母数 β と尺度母数 η を推定し、それらを用いて信頼度や故障率を求めることで、機器の寿命特性を定量的に把握することができます
さらに、ワイブルモデルによる故障確率の計算を通じて、一定期間内の故障リスクを評価し、予測保全の計画を立てる方法を紹介しました。これにより、メンテナンス戦略の最適化やコスト削減が期待できます。
ワイブル分布はシンプルながら非常に有用なツールです。正確なパラメータ推定と適切な解析を行うことで、製造業や品質管理、設備保全の現場において信頼性評価や予測保全に役立てることができます。
本記事が、皆さんの業務に少しでも役立てれば光栄です。








コメント