時系列データ分析の基本にして、もっとも直感的な手法のひとつが「移動平均(Moving Average、MA)」です。
過去のデータを一定期間で平均化し、トレンドや周期性、ノイズを滑らかに見せるこの手法は、予測や異常検知の第一歩として幅広く活用されています。
本記事では、移動平均の仕組みや種類(単純移動平均、加重移動平均、指数移動平均)をPythonで実装しながら詳しく解説します。可視化の方法やビジネス・製造現場での活用例にも触れていきますので、是非参考にしてください。
時系列データ分析全般に関する情報、他の手法について知りたい方は、「【Python実践】時系列データ分析で未来予測・異常検知・補正に挑戦!」をご一読ください。

移動平均を用いた時系列分析とは
移動平均(Moving Average)は、過去の一定期間のデータを平均化することで、時系列データのノイズを抑え、傾向や異常を見つけやすくする基本的かつ強力な分析手法です。
一定の期間内の平均値を計算し、その結果をもとに次の値を推定します。例えば、過去10日間のデータを平均化し、翌日の値を予測するという形で活用されます
移動平均は、過去のデータを使って一定期間の平均を計算するだけなので、未来の値を直接予測する能力はありません。しかし、時系列データの異常検知やデータ補正には有効な手法です。
得意な分野
✅ 短期的なトレンド分析: 最近のデータの変動をならし、傾向を視覚化することができる。
✅ ノイズ除去: データのランダムな変動を抑え、スムーズな分析が可能。
✅ 異常検知: 設定した閾値から外れた値を検出し、データの異常を識別する。
✅ データ補正: 突発的な変動や外れ値を、移動平均値で補正して安定したデータに変換。
不得意な分野
❌ 未来予測: 過去データを平均化するだけなので、長期的な予測には適さない。
❌ 季節性の考慮: 周期的な変動を考慮できないため、SARIMAや指数平滑化法のほうが適している。
❌ トレンド変化への対応: 新しいトレンドや急激な変動が苦手なため、機械学習モデルのほうが優れた予測が可能。
準備
本記事で紹介しているプログラムを実行する場合、こちらに掲載しているプログラムを実行し、ダミーデータを作成の上、各プログラムの read_csv() のファイル参照パスを適宜変更してください。
また、下記のコマンドで必要なモジュールをインストールしてください。
pip install pandas numpy matplotlib
移動平均の種類
移動平均には、計算方法の違いによっていくつかの種類があります。本記事では、代表的な3つの移動平均を取り上げ、それぞれの特徴と活用方法について解説します。
| 移動平均の種類 | 特徴 | 長所 | 短所 |
|---|---|---|---|
| SMA(単純移動平均) | 過去のデータを単純に平均化 | 計算が簡単・ノイズ除去 | 最新データの変化に鈍感 |
| WMA(加重移動平均) | 最新のデータに高い重みを付与 | トレンドを強調 | 重み設計が必要 |
| EMA(指数移動平均) | 最新データを指数的に重視 | 素早く変化に適応 | スパン設定が難しい |
本記事で紹介するPythonプログラムは、SMA(単純移動平均)を採用しています。
単純移動平均(SMA: Simple Moving Average)
最も基本的な移動平均の方法で、過去の一定期間(例:7日間)のデータの平均を取ります。すべての値を均等に扱うため、データのノイズを取り除き、全体の傾向を把握しやすくなります。
✅ 簡単に計算可能で、一定の期間にわたる平均値を算出する。
✅ 短期のノイズを除去し、長期的な傾向を把握しやすい。
❌ 最新のデータに特別な重みを付けず、過去のデータと同等に扱うため、トレンドの変化に対する感度が低い。
import pandas as pd
# 時系列データを準備
data = {"timestamp": pd.date_range(start="2025-01-01", periods=30, freq="D"),
"value": [i + (i % 5 - 2) * 2 for i in range(30)]} # ダミーデータ
df = pd.DataFrame(data)
# 単純移動平均(7日間)の計算
df["SMA"] = df["value"].rolling(window=7).mean()
print(df[["timestamp", "value", "SMA"]])加重移動平均(WMA: Weighted Moving Average)
直近のデータほど大きな重みを付けて平均を計算する方法です。最近の変化を強調できるため、トレンドの変化に迅速に対応できます。
✅ 最近のデータにより大きな重みを付けることで、最新のトレンドを強調できる。
✅ 長期のデータよりも直近のデータを重視しやすい。
❌ 重みの設計が必要であり、計算が少し複雑になる。
import numpy as np
# 重みを設定(例: 1, 2, 3, ..., windowサイズ)
window = 7
weights = np.arange(1, window + 1)
# 加重移動平均の計算
df["WMA"] = df["value"].rolling(window).apply(lambda x: np.dot(x, weights) / weights.sum(), raw=True)
print(df[["timestamp", "value", "WMA"]])指数移動平均(EMA: Exponential Moving Average)
最新のデータを指数的に重視することで、過去のデータよりも直近の値に強い影響を与える移動平均です。急激な変化を素早く反映できるため、金融市場などでよく利用されます。
✅ 過去のデータよりも最新のデータを指数的に強調し、急激なトレンド変化に適応可能。
✅ 一定の「スパン(期間)」を設定するだけで適用でき、金融市場やセンサーデータ分析に広く使われる。
❌ スパンの選び方が結果に大きく影響するため、慎重に決める必要がある。
# 指数移動平均(7日間)の計算
df["EMA"] = df["value"].ewm(span=7, adjust=False).mean()
print(df[["timestamp", "value", "EMA"]])単純移動平均による未来予測
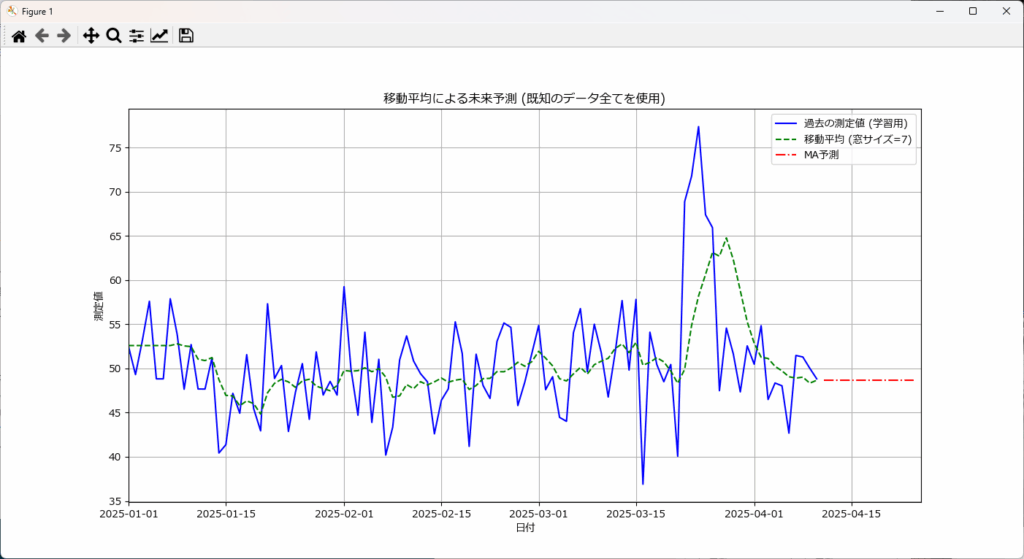
未来のデータが存在しないため、移動平均の計算が行えず、予測ができません。つまり予測できてないということです。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import os
# 日本語フォントの設定
rcParams['font.family'] = 'Meiryo' # Windowsの場合
def ma_forecast_absolute_future(df: pd.DataFrame, timestamp_col: str, value_col: str,
window: int = 10, forecast_steps: int = 7):
"""
移動平均を使った、提供されたDataFrameの最終日以降の未来を予測し、結果をプロットする。
この関数は、提供されたdfの全データを学習に使用し、その後の未観測期間を予測する。
Parameters:
df (pd.DataFrame): 時系列データのDataFrame (全データを学習に使用)
timestamp_col (str): 時刻のカラム名
value_col (str): 予測対象の数値データのカラム名
window (int): 移動平均の計算範囲
forecast_steps (int): 未来を予測するステップ数(日数)。
Returns:
pd.Series: 未来予測値を含むシリーズ
"""
# データをコピーしてインデックスを設定
df_processed = df.copy()
df_processed.set_index(timestamp_col, inplace=True)
# タイムスタンプが重複している場合は、最後の値を残す
df_processed = df_processed[~df_processed.index.duplicated(keep='last')]
# 日次データにリサンプリングし、欠損値はNaN
df_processed = df_processed.asfreq('D')
# 欠損値の補完 (線形補間、前後を埋める)
df_processed[value_col] = df_processed[value_col].interpolate(method='linear')
df_processed[value_col] = df_processed[value_col].fillna(method='bfill').fillna(method='ffill')
# 全学習データに基づいて移動平均を計算
# ここでの df_processed は、提供されたCSVの全期間を表す
data_for_ma = df_processed[value_col]
df_processed["rolling_mean"] = data_for_ma.rolling(window=window, center=False).mean()
# 最初のwindow-1個のNaNを埋める
df_processed["rolling_mean"] = df_processed["rolling_mean"].fillna(method='bfill')
print(f"\n--- 移動平均による未来予測 (窓サイズ: {window}, 予測期間: {forecast_steps}日) ---")
# 予測に使用する最後の移動平均値
if df_processed["rolling_mean"].empty:
print("エラー: 処理後のデータフレームが空です。予測できません。")
return pd.Series()
last_known_mean = df_processed["rolling_mean"].iloc[-1]
# 未来のタイムスタンプを作成 (df_processedの最終日以降)
last_known_date = df_processed.index[-1]
forecast_dates = pd.date_range(start=last_known_date + pd.Timedelta(days=1), periods=forecast_steps, freq='D')
# 未来の予測値は最後の移動平均値の繰り返し
forecast_series = pd.Series([last_known_mean] * forecast_steps, index=forecast_dates, name=value_col)
print("予測結果:")
print(forecast_series)
# グラフの表示
plt.figure(figsize=(14, 7))
plt.plot(df_processed.index, df_processed[value_col], label="過去の測定値 (学習用)", color="blue")
plt.plot(df_processed.index, df_processed["rolling_mean"], label=f"移動平均 (窓サイズ={window})", color="green", linestyle="--")
# 未来の予測をプロット (過去データの終了点から始まる)
plt.plot(forecast_series.index, forecast_series, label="MA予測", color="red", linestyle="-.")
# グラフのX軸範囲を調整して、予測部分も見えるようにする
# 最終日 + 予測ステップ数 + 少し余白
end_date_for_plot = forecast_dates[-1] + pd.Timedelta(days=1)
plt.xlim(df_processed.index[0], end_date_for_plot)
plt.xlabel("日付")
plt.ylabel("測定値")
plt.title("移動平均による未来予測 (既知のデータ全てを使用)")
plt.legend()
plt.grid(True)
plt.show()
return forecast_series
if __name__ == "__main__":
# CSVファイル名 (既存のdummy_timeseries.csvを使用)
csv_filename = "dummy_timeseries.csv"
# CSVを読み込んで関数を実行
df = pd.read_csv(csv_filename, parse_dates=["timestamp"])
# 未来予測の実行
# window: 移動平均の窓サイズ
# forecast_steps: 予測する日数(この日数のデータは過去には存在しない)
ma_predictions = ma_forecast_absolute_future(df, "timestamp", "value", window=7, forecast_steps=14)実行した結果、同じ値が出力されました。
--- 移動平均による未来予測 (窓サイズ: 7, 予測期間: 14日) ---
予測結果:
2025-04-11 48.674583
2025-04-12 48.674583
2025-04-13 48.674583
2025-04-14 48.674583
2025-04-15 48.674583
2025-04-16 48.674583
2025-04-17 48.674583
2025-04-18 48.674583
2025-04-19 48.674583
2025-04-20 48.674583
2025-04-21 48.674583
2025-04-22 48.674583
2025-04-23 48.674583
2025-04-24 48.674583
Freq: D, Name: value, dtype: float64
単純移動平均による異常検知
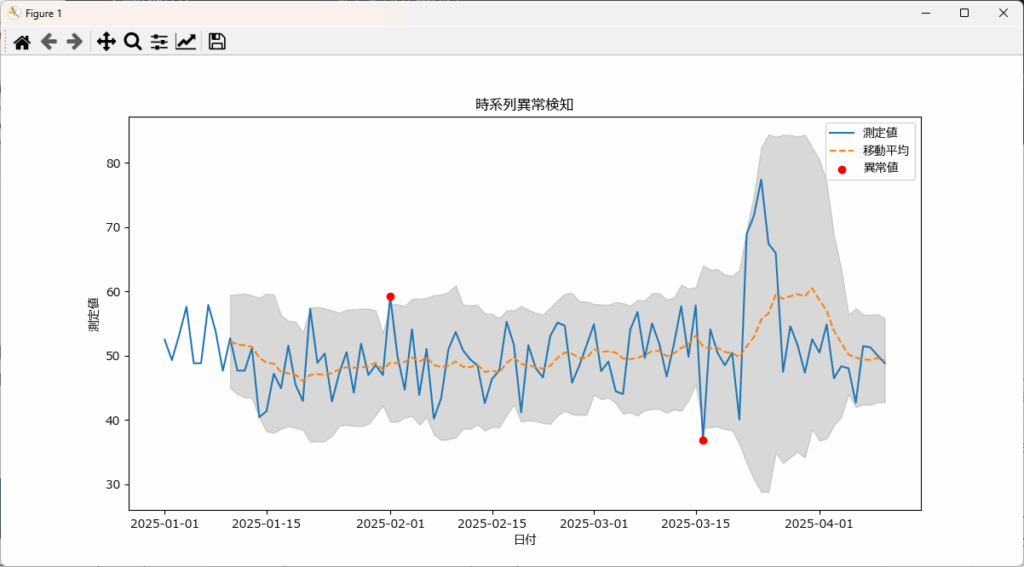
移動平均を使うことで、データの通常の傾向(基準値)を定義できます。この基準値から大きく逸脱したデータポイントは異常値として検出可能です。例えば、過去7日間の平均から±2σ(標準偏差)以上外れる値を異常とみなすという手法が使えます。
灰色の部分は、正常値の範囲を現わしています。正常値の範囲は異常検知の目的や許容範囲にもとづき決定する必要がありますが、今回は暫定的に2σ(95.45%)にしています。
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import rcParams
# 日本語フォントの設定
rcParams['font.family'] = 'Meiryo'
def detect_and_clean_anomalies(df, timestamp_col, value_col, window=10, threshold=2, correction_method="mean"):
"""
移動平均と標準偏差を使った異常検知を行い、異常値を補正・クリーニングする。
Parameters:
df (pd.DataFrame): 時系列データのDataFrame
timestamp_col (str): 時刻のカラム名
value_col (str): 分析対象の数値データのカラム名
window (int): 移動平均の計算範囲
threshold (int): 標準偏差の閾値(何σを異常とするか)
correction_method (str): 異常値の補正方法("mean" or "median")
Returns:
pd.DataFrame: 異常値を補正したデータフレーム
"""
# データをコピーしてインデックスを設定
df = df.copy()
df.set_index(timestamp_col, inplace=True)
# 移動平均と標準偏差の計算
df["mean"] = df[value_col].rolling(window).mean()
df["std"] = df[value_col].rolling(window).std()
# 異常値の検出
df["anomaly"] = (df[value_col] > df["mean"] + threshold * df["std"]) | (df[value_col] < df["mean"] - threshold * df["std"])
# 異常値データの抽出(補正前の値を保存)
anomalies_before = df[df["anomaly"]][[value_col]]
# 異常値の補正
if correction_method == "mean":
df.loc[df["anomaly"], value_col] = df["mean"][df["anomaly"]]
elif correction_method == "median":
df.loc[df["anomaly"], value_col] = df[value_col].rolling(window).median()[df["anomaly"]]
# 異常値データをCSVに保存
anomalies_before.to_csv("anomalies_before.csv")
df.to_csv("cleaned_data.csv")
print("\n補正前の異常値を 'anomalies_before.csv' に保存しました。")
print("補正後のデータを 'cleaned_data.csv' に保存しました。")
# グラフの表示
plt.figure(figsize=(12, 6))
plt.plot(df.index, df[value_col], label="補正後の測定値", color="blue")
plt.plot(df.index, df["mean"], label="移動平均", linestyle="dashed", color="green")
plt.fill_between(df.index, df["mean"] - threshold * df["std"], df["mean"] + threshold * df["std"], color="gray", alpha=0.3)
# 異常値(補正前)を赤で表示
plt.scatter(anomalies_before.index, anomalies_before[value_col], color="red", linewidths=1.5, label="異常値(補正前)", zorder=2)
# 補正された値(緑)を表示
plt.scatter(df.index[df["anomaly"]], df[value_col][df["anomaly"]], color="limegreen", edgecolors="darkgreen", linewidths=1.5, label="補正値", zorder=3)
# 日本語ラベル
plt.xlabel("日付")
plt.ylabel("測定値")
plt.title("時系列異常検知と補正")
plt.legend()
plt.show()
return df
if __name__ == "__main__":
# CSVを読み込んで関数を実行
df = pd.read_csv("dummy_timeseries.csv", parse_dates=["timestamp"])
cleaned_df = detect_and_clean_anomalies(df, "timestamp", "value", window=10, threshold=2, correction_method="mean")検出された異常値:
value mean std
timestamp
2025-02-01 59.261391 48.896132 4.582723
2025-03-16 36.901274 51.406392 6.328080
単純移動平均によるデータ補正/クリーニング
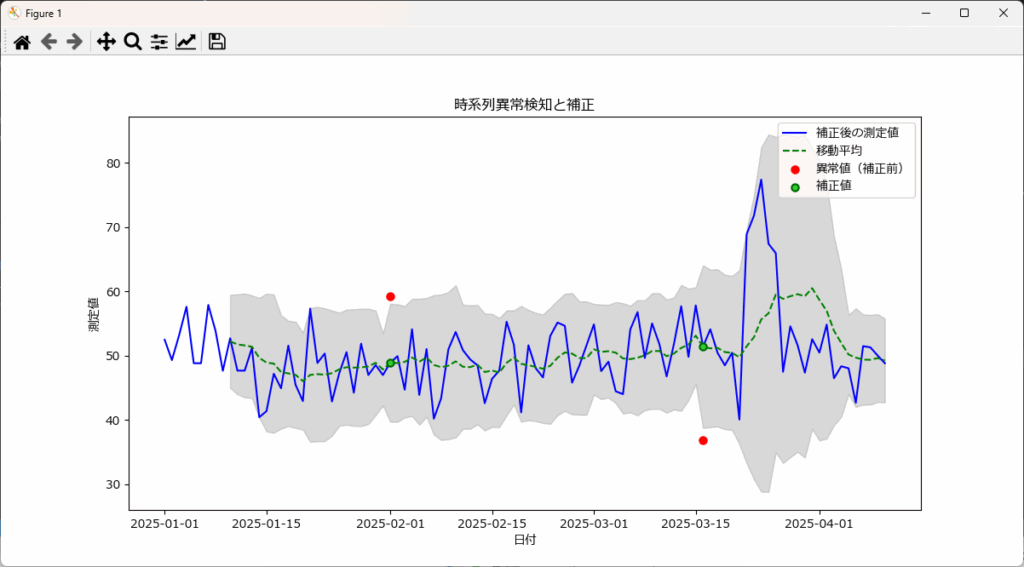
異常値が検出された場合、その値を移動平均で置き換えることで、データの修正が可能です。特に、センサー測定値や経済指標などのデータで、突発的なスパイクをならして滑らかにする目的で利用されます。これにより、ノイズを除去し、より信頼性の高いデータ分析が可能になります
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import rcParams
# 日本語フォントの設定
rcParams['font.family'] = 'Meiryo'
def detect_and_clean_anomalies(df, timestamp_col, value_col, window=10, threshold=2, correction_method="mean"):
"""
移動平均と標準偏差を使った異常検知を行い、異常値を補正・クリーニングする。
Parameters:
df (pd.DataFrame): 時系列データのDataFrame
timestamp_col (str): 時刻のカラム名
value_col (str): 分析対象の数値データのカラム名
window (int): 移動平均の計算範囲
threshold (int): 標準偏差の閾値(何σを異常とするか)
correction_method (str): 異常値の補正方法("mean" or "median")
Returns:
pd.DataFrame: 異常値を補正したデータフレーム
"""
# データをコピーしてインデックスを設定
df = df.copy()
df.set_index(timestamp_col, inplace=True)
# 移動平均と標準偏差の計算
df["mean"] = df[value_col].rolling(window).mean()
df["std"] = df[value_col].rolling(window).std()
# 異常値の検出
df["anomaly"] = (df[value_col] > df["mean"] + threshold * df["std"]) | (df[value_col] < df["mean"] - threshold * df["std"])
# 異常値データの抽出(補正前の値を保存)
anomalies_before = df[df["anomaly"]][[value_col]]
# 異常値の補正
if correction_method == "mean":
df.loc[df["anomaly"], value_col] = df["mean"][df["anomaly"]]
elif correction_method == "median":
df.loc[df["anomaly"], value_col] = df[value_col].rolling(window).median()[df["anomaly"]]
# 異常値データをCSVに保存
anomalies_before.to_csv("anomalies_before.csv")
df.to_csv("cleaned_data.csv")
print("\n補正前の異常値を 'anomalies_before.csv' に保存しました。")
print("補正後のデータを 'cleaned_data.csv' に保存しました。")
# グラフの表示
plt.figure(figsize=(12, 6))
plt.plot(df.index, df[value_col], label="補正後の測定値", color="blue")
plt.plot(df.index, df["mean"], label="移動平均", linestyle="dashed", color="green")
plt.fill_between(df.index, df["mean"] - threshold * df["std"], df["mean"] + threshold * df["std"], color="gray", alpha=0.3)
# 異常値(補正前)を赤で表示
plt.scatter(anomalies_before.index, anomalies_before[value_col], color="red", alpha=0.6, edgecolors="red", linewidths=1.5, label="異常値(補正前)", zorder=2)
# 補正された値(緑)を表示
plt.scatter(df.index[df["anomaly"]], df[value_col][df["anomaly"]], color="limegreen", edgecolors="darkgreen", linewidths=1.5, label="補正値", zorder=3)
# 日本語ラベル
plt.xlabel("日付")
plt.ylabel("測定値")
plt.title("時系列異常検知と補正")
plt.legend()
plt.show()
return df
if __name__ == "__main__":
# CSVを読み込んで関数を実行
df = pd.read_csv("dummy_timeseries.csv", parse_dates=["timestamp"])
cleaned_df = detect_and_clean_anomalies(df, "timestamp", "value", window=10, threshold=2, correction_method="mean")補正前の異常値を 'anomalies_before.csv' に保存しました。
補正後のデータを 'cleaned_data.csv' に保存しました。
まとめ
移動平均(Moving Average)は、時系列データ分析の第一歩として非常に有用な手法です。過去データの平均を活用することで、短期的なトレンドを可視化し、ノイズの多いデータから意味のある傾向を抽出できます。
特に、異常検知やデータ補正といった実務的な課題に対しては、シンプルかつ効果的なアプローチを提供してくれます。
ただし、移動平均は未来の値を「予測する」機能に乏しく、急激なトレンドの変化や季節性のあるデータへの対応には限界があります。そのため、より高度な時系列モデル(例:SARIMAや指数平滑化法、機械学習モデル)との使い分けが重要です。









コメント