この記事では、過去のデータに重みをつけながら平均を取ることで、未来を予測したり異常を検知したりできる「指数平滑化法(Exponential Smoothing, ES)」について、Pythonコード付きでわかりやすく解説します。
「時系列分析に興味はあるけど、ARIMA や LSTM はちょっとハードルが高い…」そんな方にぴったりの、シンプルで実践的な手法です。
時系列データ分析全般に関する情報、他の手法について知りたい方は、「【Python実践】時系列データ分析で未来予測・異常検知・補正に挑戦!」をご一読ください。

指数平滑化法(ES)とは
指数平滑化法(Exponential Smoothing, ES)は、過去のデータの重みを指数的に減衰させながら平均化する手法です。具体的には、時間が経過するにつれて古いデータほど影響を小さくし、最新のデータをより強く反映させる仕組みになっています。
指数平滑化法は、ARIMAや機械学習モデルほど複雑ではないですが、リアルタイムデータ分析や異常検知のベースラインとしては非常に有効な手法です。また、後述するSARIMAのような複雑な統計的モデルに比べて、パラメータの選定が比較的直感的で、初心者にも扱いやすいというメリットがあります。
得意な分野
✅ 短期予測: 直近のデータを強く反映するため、短期間の未来予測が適している。
✅ リアルタイム分析: 過去データの影響を指数的に減衰させることで、動的に変化するトレンドを捉えやすい。
✅ 異常検知: 予測値と実測値の差を分析することで、異常値を検出するベースラインを作成できる。
✅ 扱いやすさ: モデルの構造が比較的シンプルで、初心者でも導入しやすい。
不得意な分野
❌ 長期予測: 短期間のデータに重点を置くため、長期的なトレンドの変化には対応しにくい。
❌ 季節性の考慮: 単純なESでは周期的な変動を考慮できないため、SARIMAなどの季節性モデルの併用が必要。
❌ 非線形なデータ: トレンドが急激に変化する場合や、非線形な構造を持つデータには適応が難しい。
準備
本記事で紹介しているプログラムを実行する場合、こちらに掲載しているプログラムを実行し、ダミーデータを作成の上、各プログラムの read_csv() のファイル参照パスを適宜変更してください。
また、下記のコマンドで必要なモジュールをインストールしてください。
pip install pandas numpy matplotlib statsmodels
指数平滑化法(ES)による未来予測
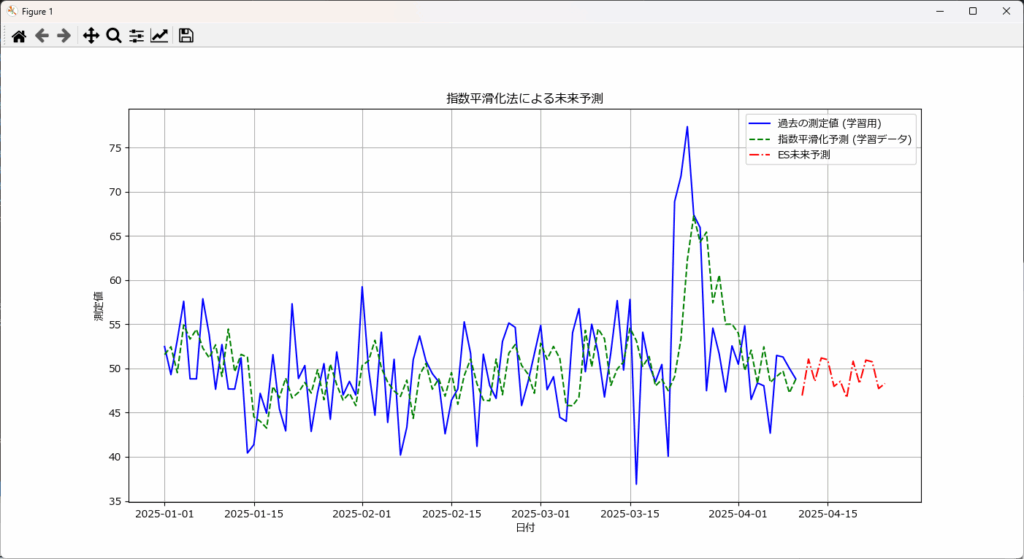
上記のグラフは、指数平滑化法(Exponential Smoothing) を用いた未来予測の結果です。
実際の測定値の細かなノイズを吸収し、全体的により平滑化された動きを示しています。これは、突発的な変動(3月下旬のスパイクなど)に過度に反応せず、基盤となるトレンドや周期性を捉えようとする特性によるものです。
プログラムでseasonal_periods=7(7日周期の季節性)と設定しているため、週単位の周期的なパターンが予測に反映されています。未来予測(赤い破線)にもその傾向が見られます。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
from statsmodels.tsa.api import ExponentialSmoothing
import warnings
warnings.filterwarnings("ignore") # 警告メッセージを非表示
# 日本語フォントの設定
rcParams['font.family'] = 'Meiryo'
def es_forecast_absolute_future(df: pd.DataFrame, timestamp_col: str, value_col: str,
seasonal_periods: int = 7, forecast_steps: int = 14,
trend_type: str = "add", seasonal_type: str = "add"):
"""
指数平滑化法(Holt-Winters)を使用して時系列データの未来予測を行う。
Parameters:
df (pd.DataFrame): 時系列データのDataFrame (全データを学習に使用)
timestamp_col (str): 時刻のカラム名
value_col (str): 予測対象の数値データのカラム名
seasonal_periods (int): 季節性の周期(例: 日次データで週次なら7)。
forecast_steps (int): 未来を予測するステップ数(日数)。
trend_type (str): トレンドの適用方法("add" または "mul")。
seasonal_type (str): 季節性の適用方法("add" または "mul")。
Returns:
pd.Series: 未来予測値を含むシリーズ
"""
# データをコピーしてインデックスを設定
df_processed = df.copy()
df_processed.set_index(timestamp_col, inplace=True)
# 欠損値の処理
df_processed[value_col] = df_processed[value_col].interpolate(method="linear").fillna(method="bfill").fillna(method="ffill")
# 指数平滑化モデルの適用
print(f"\n--- 指数平滑化法による未来予測 (季節周期: {seasonal_periods}, 予測期間: {forecast_steps}日) ---")
try:
model = ExponentialSmoothing(
df_processed[value_col],
seasonal_periods=seasonal_periods,
trend=trend_type,
seasonal=seasonal_type,
initialization_method="estimated"
)
model_fit = model.fit()
print("指数平滑化モデルの学習が完了しました。")
except Exception as e:
print(f"指数平滑化モデルの学習中にエラーが発生しました: {e}")
return pd.Series()
# 未来のタイムスタンプを作成
last_known_date = df_processed.index[-1]
forecast_dates = pd.date_range(start=last_known_date + pd.Timedelta(days=1), periods=forecast_steps, freq="D")
# 未来予測値を取得
forecast_values = model_fit.forecast(steps=forecast_steps)
# 予測結果をデータフレームに格納
forecast_series = pd.Series(forecast_values, index=forecast_dates, name=value_col)
print("予測結果:")
print(forecast_series)
# グラフの表示
plt.figure(figsize=(14, 7))
plt.plot(df_processed.index, df_processed[value_col], label="過去の測定値 (学習用)", color="blue")
plt.plot(df_processed.index, model_fit.fittedvalues, label="指数平滑化予測 (学習データ)", color="green", linestyle="--")
plt.plot(forecast_series.index, forecast_series, label="ES未来予測", color="red", linestyle="-.")
plt.xlabel("日付")
plt.ylabel("測定値")
plt.title("指数平滑化法による未来予測")
plt.legend()
plt.grid(True)
plt.show()
return forecast_series
if __name__ == "__main__":
# CSVを読み込んで関数を実行
csv_filename = "dummy_timeseries.csv"
df = pd.read_csv(csv_filename, parse_dates=["timestamp"])
# 未来予測の実行
es_predictions = es_forecast_absolute_future(df, "timestamp", "value", seasonal_periods=7, forecast_steps=14)--- 指数平滑化法による未来予測 (季節周期: 7, 予測期間: 14日) ---
指数平滑化モデルの学習が完了しました。
予測結果:
2025-04-11 46.935424
2025-04-12 51.064841
2025-04-13 48.551949
2025-04-14 51.192205
2025-04-15 50.996848
2025-04-16 47.974951
2025-04-17 48.550608
2025-04-18 46.695356
2025-04-19 50.824773
2025-04-20 48.311880
2025-04-21 50.952136
2025-04-22 50.756779
2025-04-23 47.734882
2025-04-24 48.310539
Freq: D, Name: value, dtype: float64
指数平滑化法(ES)による異常検知
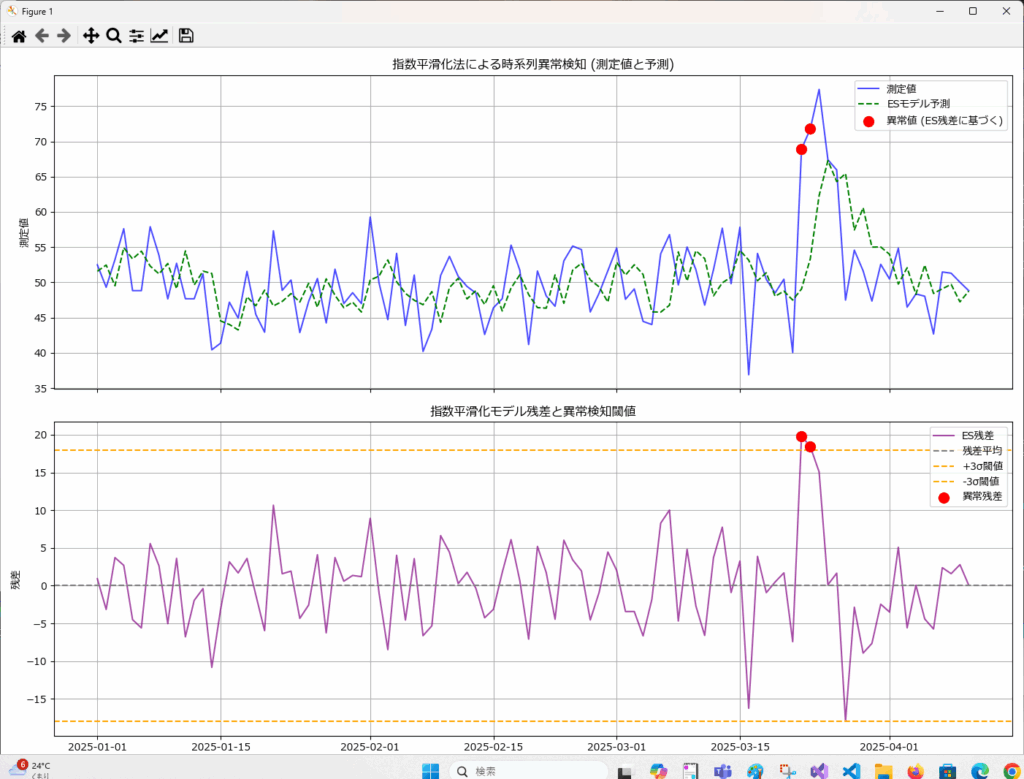
平滑化された予測値と実際の値の乖離が、一定の閾値(例えば平均±2σ)を超えた場合、異常と判断します。
上のグラフは予測と実績のプロット、下のグラフは予測との差(残差)をプロットしたものです。
残差が閾値(この場合は+3σ)を超えた個所が異常値と判断されていることが分かります。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
from statsmodels.tsa.api import ExponentialSmoothing
import warnings
warnings.filterwarnings("ignore") # 警告メッセージを非表示にする
# 日本語フォントの設定 (お使いの環境に合わせて適宜変更してください)
rcParams['font.family'] = 'Meiryo' # Windowsの場合
# rcParams['font.family'] = 'AppleGothic' # Macの場合
# rcParams['font.family'] = 'DejaVu Sans' # デフォルト、日本語対応しない場合がある
def es_anomaly_detection(df: pd.DataFrame, time_col: str, value_col: str,
seasonal_periods: int, threshold_sigma: int = 3,
trend_type: str = 'add', seasonal_type: str = 'add'):
"""
指数平滑化法(Holt-Winters)を使用して時系列データの異常検知を行います。
Args:
df (pd.DataFrame): 処理するデータフレーム。
time_col (str): タイムスタンプの列名。
value_col (str): 時系列データの値の列名。
seasonal_periods (int): 季節周期の長さ(例: 日次データで週次傾向なら7)。
threshold_sigma (int, optional): 異常値を判断するための残差の標準偏差の倍数。デフォルトは3。
trend_type (str, optional): トレンドのタイプ ('add' または 'mul')。デフォルトは'add'。
seasonal_type (str, optional): 季節性のタイプ ('add' または 'mul')。デフォルトは'add'。
Returns:
pd.DataFrame: 'es_prediction', 'residuals', 'is_anomaly' 列が追加されたデータフレーム。
"""
# タイムスタンプ列をインデックスに設定
df_processed = df.set_index(time_col).copy()
# 指数平滑化モデル (Holt-Winters) の適用
print(f"--- 指数平滑化モデルの適用 (Trend: {trend_type}, Seasonal: {seasonal_type}, Period: {seasonal_periods}) ---")
try:
# ExponentialSmoothingモデルは、内部でレベル、トレンド、季節性の各成分を平滑化する
# initialization_method="estimated" は、モデルの初期値をデータから推定させる設定
model = ExponentialSmoothing(
df_processed[value_col],
seasonal_periods=seasonal_periods,
trend=trend_type,
seasonal=seasonal_type,
initialization_method="estimated"
)
model_fit = model.fit()
print("指数平滑化モデルの学習が完了しました。")
# print(model_fit.summary()) # モデルのサマリーを表示したい場合はコメントを解除
except Exception as e:
print(f"指数平滑化モデルの学習中にエラーが発生しました: {e}")
return None
# モデルの学習データ期間内の予測値を取得
# これがベースライン(期待される値)となる
df_processed['es_prediction'] = model_fit.fittedvalues
# 残差(実際の値 - 予測値)を計算
df_processed['residuals'] = df_processed[value_col] - df_processed['es_prediction']
# 残差の平均と標準偏差を計算 (異常値検知の閾値設定に使用)
# 残差の平均は通常0に近いですが、念のため計算に含めます
residual_mean = df_processed['residuals'].mean()
residual_std = df_processed['residuals'].std()
# 異常検知 (残差の閾値設定)
# 残差が平均から threshold_sigma 標準偏差以上離れている場合を異常とする
df_processed['is_anomaly'] = (df_processed['residuals'] > residual_mean + threshold_sigma * residual_std) | \
(df_processed['residuals'] < residual_mean - threshold_sigma * residual_std)
# 検出された異常値の表示
anomalies = df_processed[df_processed['is_anomaly']]
if not anomalies.empty:
print("\n--- 検出された異常値 ---")
print(anomalies[[value_col, 'es_prediction', 'residuals', 'is_anomaly']])
else:
print("\n--- 異常値は検出されませんでした ---")
# --- 結果の可視化 (グラフを縦に並べる) ---
fig, axes = plt.subplots(nrows=2, ncols=1, figsize=(14, 10), sharex=True) # 2行1列でグラフを配置
# 1つ目のサブプロット: 測定値と指数平滑化予測
axes[0].plot(df_processed.index, df_processed[value_col], label='測定値', color='blue', alpha=0.7)
axes[0].plot(df_processed.index, df_processed['es_prediction'], label='ESモデル予測', color='green', linestyle='--')
if not anomalies.empty:
axes[0].scatter(anomalies.index, anomalies[value_col], color='red', s=100, zorder=5, label='異常値 (ES残差に基づく)')
axes[0].set_title('指数平滑化法による時系列異常検知 (測定値と予測)')
axes[0].set_ylabel('測定値')
axes[0].legend()
axes[0].grid(True)
# 2つ目のサブプロット: 残差と閾値
axes[1].plot(df_processed.index, df_processed['residuals'], label='ES残差', color='purple', alpha=0.7)
axes[1].axhline(residual_mean, color='gray', linestyle='--', label='残差平均')
axes[1].axhline(residual_mean + threshold_sigma * residual_std, color='orange', linestyle='--', label=f'+{threshold_sigma}σ閾値')
axes[1].axhline(residual_mean - threshold_sigma * residual_std, color='orange', linestyle='--', label=f'-{threshold_sigma}σ閾値')
if not anomalies.empty:
axes[1].scatter(anomalies.index, anomalies['residuals'], color='red', s=100, zorder=5, label='異常残差')
axes[1].set_title('指数平滑化モデル残差と異常検知閾値')
axes[1].set_xlabel('日付')
axes[1].set_ylabel('残差')
axes[1].legend()
axes[1].grid(True)
plt.tight_layout() # サブプロット間のスペースを自動調整
plt.show()
return df_processed
# --- メインの実行部分 ---
if __name__ == "__main__":
# CSVを読み込んで関数を実行
# dummy_timeseries.csvが既に存在することを前提とします。
df = pd.read_csv("dummy_timeseries.csv", parse_dates=["timestamp"])
# 指数平滑化モデルのパラメータ (例: 季節周期が7日と仮定)
# これらのパラメータは、実際のデータの特性に基づいて調整が必要です。
# あなたのデータにはトレンドと季節性が見られるため、Holt-Winters (ExponentialSmoothing) が適切です。
es_seasonal_periods = 7 # 週次季節性を想定
# トレンドと季節性のタイプを決定 ('add' (加法的) または 'mul' (乗法的))
# 'add'は変動幅が一定の場合、'mul'は変動幅がデータ値に比例して大きくなる場合
es_trend_type = 'add'
es_seasonal_type = 'add' # または 'mul' を試すこともできます
# 関数を呼び出す
result_df = es_anomaly_detection(df,
time_col="timestamp",
value_col="value",
seasonal_periods=es_seasonal_periods,
threshold_sigma=3, # 閾値を3σに設定
trend_type=es_trend_type,
seasonal_type=es_seasonal_type)
if result_df is not None:
print("\n--- 関数実行結果 (異常値検出フラグ含む) ---")
print(result_df.tail())--- 指数平滑化モデルの適用 (Trend: add, Seasonal: add, Period: 7) ---
指数平滑化モデルの学習が完了しました。
--- 検出された異常値 ---
value es_prediction residuals is_anomaly
timestamp
2025-03-22 68.901641 49.073300 19.828340 True
2025-03-23 71.785563 53.356988 18.428575 True
指数平滑化法(ES)によるデータ補正/クリーニング
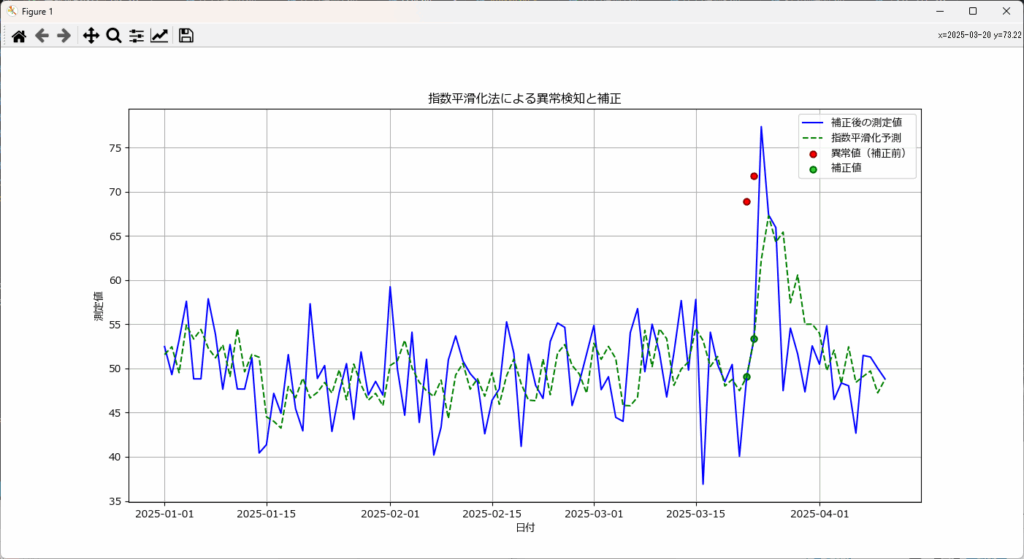
これを、
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
from statsmodels.tsa.api import ExponentialSmoothing
# 日本語フォントの設定
rcParams['font.family'] = 'Meiryo'
def es_anomaly_detection_and_cleaning(df: pd.DataFrame, time_col: str, value_col: str,
seasonal_periods: int, threshold_sigma: int = 3,
trend_type: str = "add", seasonal_type: str = "add",
correction_method: str = "mean"):
"""
指数平滑化法(Holt-Winters)を使用して時系列データの異常検知を行い、異常値を補正・クリーニングする。
Args:
df (pd.DataFrame): 処理するデータフレーム。
time_col (str): タイムスタンプの列名。
value_col (str): 時系列データの値の列名。
seasonal_periods (int): 季節周期の長さ(例: 日次データで週次傾向なら7)。
threshold_sigma (int): 異常値を判断するための標準偏差の倍数。デフォルトは3。
trend_type (str): トレンドのタイプ ('add' または 'mul')。
seasonal_type (str): 季節性のタイプ ('add' または 'mul')。
correction_method (str): 異常値の補正方法("mean" or "median")。
Returns:
pd.DataFrame: 異常値が補正されたデータフレーム。
"""
# タイムスタンプをインデックスに設定
df_processed = df.set_index(time_col).copy()
# 指数平滑化モデルの適用
print(f"--- 指数平滑化モデルの適用 (Trend: {trend_type}, Seasonal: {seasonal_type}, Period: {seasonal_periods}) ---")
try:
model = ExponentialSmoothing(
df_processed[value_col],
seasonal_periods=seasonal_periods,
trend=trend_type,
seasonal=seasonal_type,
initialization_method="estimated"
)
model_fit = model.fit()
print("指数平滑化モデルの学習が完了しました。")
except Exception as e:
print(f"指数平滑化モデルの学習中にエラーが発生しました: {e}")
return None
# 予測値を取得
df_processed["es_prediction"] = model_fit.fittedvalues
# 残差(予測値との差)を計算
df_processed["residuals"] = df_processed[value_col] - df_processed["es_prediction"]
# 残差の平均と標準偏差を計算
residual_mean = df_processed["residuals"].mean()
residual_std = df_processed["residuals"].std()
# 異常値の検出
df_processed["is_anomaly"] = (df_processed["residuals"] > residual_mean + threshold_sigma * residual_std) | \
(df_processed["residuals"] < residual_mean - threshold_sigma * residual_std)
# 異常値の保存(補正前)
anomalies_before = df_processed[df_processed["is_anomaly"]].copy()
# 異常値を補正
if correction_method == "mean":
df_processed.loc[df_processed["is_anomaly"], value_col] = df_processed["es_prediction"][df_processed["is_anomaly"]]
elif correction_method == "median":
df_processed.loc[df_processed["is_anomaly"], value_col] = df_processed[value_col].rolling(seasonal_periods).median()[df_processed["is_anomaly"]]
# グラフの表示
plt.figure(figsize=(14, 7))
plt.plot(df_processed.index, df_processed[value_col], label="補正後の測定値", color="blue")
plt.plot(df_processed.index, df_processed["es_prediction"], label="指数平滑化予測", color="green", linestyle="--")
# 異常値(補正前)を赤で表示
if not anomalies_before.empty:
plt.scatter(anomalies_before.index, anomalies_before[value_col], color="red", edgecolors="darkred", linewidths=1.5, label="異常値(補正前)")
# 補正後の値を緑で表示
plt.scatter(df_processed.index[df_processed["is_anomaly"]], df_processed[value_col][df_processed["is_anomaly"]],
color="limegreen", edgecolors="darkgreen", linewidths=1.5, label="補正値")
plt.xlabel("日付")
plt.ylabel("測定値")
plt.title("指数平滑化法による異常検知と補正")
plt.legend()
plt.grid(True)
plt.show()
return df_processed
# --- メインの実行部分 ---
if __name__ == "__main__":
# CSVを読み込んで関数を実行
df = pd.read_csv("dummy_timeseries.csv", parse_dates=["timestamp"])
# 異常検知 + データ補正を実施
cleaned_df = es_anomaly_detection_and_cleaning(df,
time_col="timestamp",
value_col="value",
seasonal_periods=7,
threshold_sigma=3,
trend_type="add",
seasonal_type="add",
correction_method="mean")
if cleaned_df is not None:
print("\n--- 補正後のデータ ---")
print(cleaned_df.tail())--- 指数平滑化モデルの適用 (Trend: add, Seasonal: add, Period: 7) ---
指数平滑化モデルの学習が完了しました。
--- 補正後のデータ ---
value es_prediction residuals is_anomaly
timestamp
2025-04-06 42.682425 48.429619 -5.747194 False
2025-04-07 51.480601 49.099904 2.380697 False
2025-04-08 51.305276 49.720581 1.584695 False
2025-04-09 50.025567 47.241871 2.783696 False
2025-04-10 48.827064 48.771699 0.055366 False
まとめ
指数平滑化法(Exponential Smoothing, ES)は、時系列データの分析において、シンプルながらも非常に強力な予測・異常検知手法です。特にHolt-Winters法を用いることで、トレンドや季節性を考慮したモデル構築が可能となり、現場でのリアルタイムな意思決定や、異常なデータの早期発見に役立ちます。
本記事では、Pythonとstatsmodelsライブラリを活用して、未来予測と異常検知を実装する具体的な方法を紹介しました。特に短期予測や日々の運用モニタリングなど、機械学習ほどの複雑さを必要としないシーンで、ESは非常に有用です。
ただし、長期的な予測や複雑な季節性のあるデータでは、SARIMAや機械学習ベースのモデルとの併用が検討されるべきです。データの特性や目的に応じて、適切な手法を選択することが重要です。
指数平滑化法は、これから時系列分析に取り組みたい方にとって、入り口として最適な手法の一つです。ぜひ実際のデータに適用し、その効果を試してみて下さい。









コメント