センサーやログなど、膨大な時系列データを扱う現場では、「どの変数が予測に効いているのか?」を見極めることが、モデル精度を左右する最重要ポイントです。
特にアンサンブル回帰モデル(LightGBMやXGBoostなど)を使う場合、単に相関の高い特徴量を選ぶだけでは不十分。非線形性・冗長性・安定性・多様性といった観点から、特徴量を設計・評価する必要があります。
本記事では、回帰モデルにおける特徴量選定の実践的な手順を、特徴量候補選定、冗長性除去・重要性評価の3ステップに分けて解説します。
特徴量選定の考え方
アンサンブル回帰における特徴量の役割とは
アンサンブル回帰(例:LightGBM、XGBoost、ランダムフォレストなど)は、複数の弱学習器を組み合わせることで、単一モデルよりも高い予測精度と汎化性能を実現する手法です。
このとき、どの特徴量を使うかは、モデルの性能に直結する極めて重要な設計要素です。
アンサンブル回帰における特徴量の役割は、単に「目的変数との関係が強い」だけでは不十分です。以下の3つの観点が特に重要になります:
- 情報量(informativeness):目的変数の予測にどれだけ貢献するか
- 多様性(diversity):異なるモデルや木構造に異なる視点を与えるか
- 安定性(stability):データ分割やノイズに対して重要度が安定しているか
この3点を満たす特徴量こそが、アンサンブル回帰に「効く」特徴量です。
単一モデルとの違い(精度だけでなく多様性と安定性が鍵)
単一モデル(例:線形回帰、決定木など)では、特徴量の選定基準は比較的シンプルです。目的変数との相関が高い、分散が大きい、線形性がある、といった観点で評価できます。
しかし、アンサンブル回帰では事情が異なります。
| 観点 | 単一モデル | アンサンブル回帰 |
|---|---|---|
| 目的 | 単体モデルの精度最大化 | 複数モデルの総合精度と汎化性能の最大化 |
| 特徴量の評価軸 | 情報量(相関・係数) | 情報量+多様性+安定性 |
| 冗長性の扱い | 許容されることもある | 冗長な特徴量はアンサンブル効果を打ち消す可能性あり |
| 重要度の解釈 | 単一モデルでの寄与度 | モデル間での一貫性と補完性が重要 |
たとえば、相関の高い特徴量が複数あると、単一モデルでは精度が上がるかもしれませんが、アンサンブルでは分岐が分散して重要度が薄まることがあります。
また、あるモデルでは効かないが、別のモデルでは効くような特徴量(=多様性を生む特徴量)は、アンサンブル全体の性能を押し上げる鍵になります。
回帰問題における特徴量の評価軸(相関・分散・非線形性)
回帰問題では、目的変数が連続値であるため、特徴量の評価にも連続的な関係性を捉える指標が求められます。以下に、代表的な評価軸を紹介します。
相関係数(Pearson/Spearman)
- Pearson:線形関係の強さを測る
- Spearman:単調な関係性(非線形含む)を評価できる
- 高すぎる相関は冗長性のサインにもなるため、相関行列での可視化と併用が有効
分散・IQR(情報量の粗いスクリーニング)
- 分散が極端に小さい(定数に近い)特徴量は除外候補
- IQR(四分位範囲)で外れ値の影響を抑えた変動性評価も有効
非線形性の検出(モデルベース評価)
- GBDT系モデルで
feature_importance_を確認 - 相関が低くても、非線形な分岐で効く特徴量が見つかることがある
- Permutation Importance(シャッフル検証)でモデル依存性を補完
特徴量選定で必要な3つのステップ
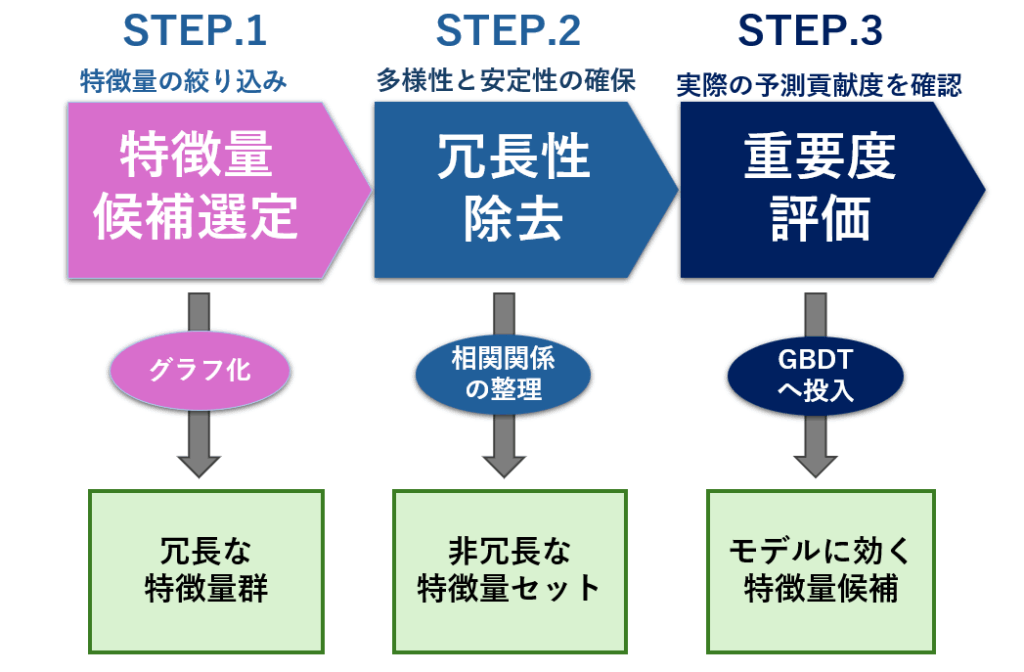
特徴量の選定手順は、以下の3つのステップで行います。
- 特徴量候補の選定
時系列データから予測に使えそうな変数を抽出し、候補群を構築します。 - 冗長性の除去と安定性・多様性の確認
必要に応じて、相関やVIFなどを用いて重複や多重共線性の存在を確認します。 - 重要度の評価
GBDTモデルに投入し、SplitやGainなどの指標で予測に寄与する特徴量を見極めます。
それぞれについてコピペ可能なサンプルプログラムを掲載していますので、合わせてご利用ください。
特徴量候補選定
全ての特徴量の中から「モデルにとって意味のあるパターンを持たない、情報価値の低い特徴量」を除外します。
これは、予測に寄与しない特徴量を早期に排除することで、後続の冗長性分析やモデル構築の効率を高めるためです。
具体的には、各特徴量ごとに以下の4種類のグラフ(箱ひげ図・ヒストグラム・散布図・折れ線)を用い、分布や目的変数との関係性を確認します。
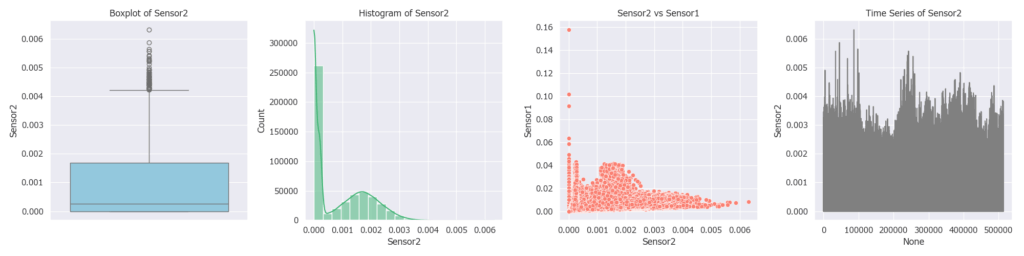
このグラフを作成するプログラムは、こちら から入手可能です。
以下の観点で4つのグラフを精査します。
| グラフ種類 | 見える特徴 | 候補になる理由 |
|---|---|---|
| 箱ひげ図 | 外れ値が明確に存在する/ばらつきが大きい | 極端値が予測に効く可能性がある(異常検知・ピーク予測など) |
| ヒストグラム | 分布が偏っている/多峰性がある | 非線形な分岐やクラスタ構造がモデルに効く可能性がある |
| 散布図(目的変数 vs 特徴量) | 緩やかな傾向(線形・非線形)が見える | 目的変数との関係性がある=予測に貢献しやすい |
| 折れ線(時系列プロット) | 明確な周期性・トレンド・急変動がある | 時系列的な変化が予測に寄与する(変化量・ピーク抽出などに活用) |
箱ひげ図で中央値に集中しすぎている → 情報量が少ない
ヒストグラムが完全に一様分布 → モデルが分岐しづらい
散布図で目的変数との関係が完全にランダム → 予測に寄与しない
折れ線がノイズ的で周期性もトレンドもない → 時系列特徴量としての価値が低い
冗長性除去
冗長性とは、強い相関をもつ特徴量が複数含まれる状態を指します。
決定木系のアンサンブル学習では、冗長性があってもモデル性能に大きく影響することは少ないものの、学習が非効率になったり、特徴量重要度が分散して解釈性が低下する可能性があります。
そのため、精度向上よりも「解釈性の向上」や「モデルの簡素化」を目的として、冗長な特徴量を適切に除去することは有用です。
冗長性除去は、以下の手順を踏みます。
- 相関係数やクラスタリングで「似ている特徴量群」を見つける
- VIFなどで数値的な冗長性を確認しておく
- 上記作業の結果とドメイン知識を総合して「あきらかに不要と思われるもの」を選ぶ
VIF(分散膨張係数)は、特徴量同士の相関関係がどれだけ高いか(多重共線性)を数値で示す指標で「この特徴量は他の特徴量とどれだけ似ているか」を測るものです。
VIF = 1 の場合は無関係、5〜10 を超える場合は冗長性が高く、非常に似通った存在であると言えます。
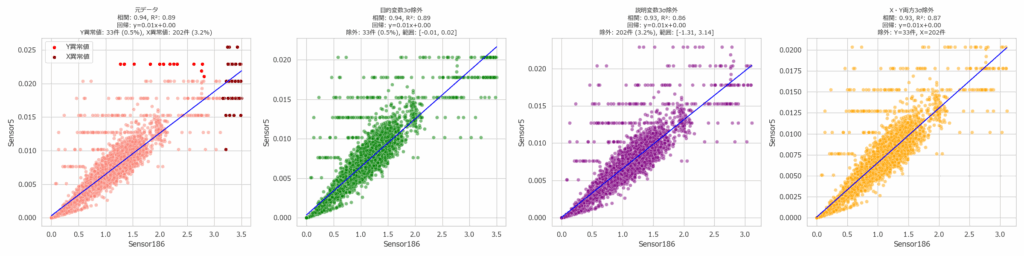
相関関係は目的変数と説明変数の散布図を作成することになりますが、目的変数、説明変数それぞれに異常値が含まれている場合、グラフの形が正しく見えません。そこで、左から「異常値有り」「目的変数異常値除外」「説明変数異常値除外」「目的変数&説明変数異常値除外」の4通りを作成するようにしました。
このグラフを作成するプログラムは、こちらから入手可能です。
下記のグラフは、Sensor1(目的変数)に対して、候補となる特徴量を対象に、相関係数・クラスタ・VIF(分散膨張係数)の3つの観点から相互作用を可視化したものです。
- Y軸=目的変数との相関係数:値が高いほど強い関係を持つ。
- 点の色=クラスタ分類:似た相関パターンを持つ特徴量群を示す。
- 点のサイズ=VIF:サイズが大きいほど他の特徴量と重複している可能性が高く、冗長性の指標となる。
下記グラフを作成するプログラムは、こちら から入手可能です。

このグラフを元に、特徴量の候補を精査します。グラフからは、クラスタ2におけるSensor30とSensor117のVIFが大きいことから、この2つの間で相関が高いことが想像できます。除去するならこの2つのどちらかが候補になります。
更に特徴量を絞り込みたい場合、クラスタごとに不要なものを除外していくことになりますが、決定木系のアンサンブル回帰は相関関係を考慮しないことや多様性の観点から、相関が低いことを理由に除外候補にすべきではありません。
ここはドメイン知識をつかって除外候補を選定すべきです。
決定木系のアンサンブル回帰では、相関が高い特徴量だけに絞るのではなく、相関の強弱に幅を持たせた特徴量をバランスよく選ぶことが重要です。特に目的変数と負の相関を持つ特徴量はモデルに多様性を与えるため、積極的に活用すると効果的です。
重要度評価
前章までで、情報量の少ない特徴量を除外し、冗長な特徴量をクラスタごとに代表化することで、入力候補を絞り込みました。
次に、GBDT(勾配ブースティング決定木)を用いて、予測性能に基づく特徴量の重要度を評価します。
GBDTモデルを使う理由は以下の通りです。
非線形な関係性や交互作用を捉えられる→ 相関やVIFでは見えない予測貢献を検出可能
特徴量の分岐貢献度を定量化できる→ どの特徴量が予測にどれだけ寄与しているかを明示的に把握できる
モデル構築と特徴量選定を同時に進められる→ 実運用に近い形で評価可能
具体的には、次の手順で進めます。
- 特徴量セットを用意する
- 前段で選定された特徴量(情報量があり、冗長性が低いもの)を使います
- 必要に応じて、目的変数(ターゲット)と結合して学習データを構成します - GBDTモデルを学習させる
- LightGBMやXGBoostなどのGBDT系モデルを使って、目的変数を予測するモデルを構築します
- 例:回帰ならLGBMRegressor、分類ならLGBMClassifier - 特徴量の重要度を出力する
- モデルが「どの特徴量をどれだけ使ったか」をスコアとして出力します
- Gain:分岐での貢献度(よく使われた特徴量ほど高い)
- Split:分岐に使われた回数(使用頻度) - SHAP(SHapley Additive exPlanations)値を算出する(予測寄与度の解釈)
各特徴量が予測にどの程度寄与したかを算出します
- グローバル解釈:全体で効いている特徴量を把握
- ローカル解釈:個別サンプルで「なぜその予測値になったか」を説明 - 重要度の高い特徴量を選定する
- 上位の特徴量を抽出し、予測に効いているものを最終候補とします
- 必要に応じて、重要度の低い特徴量を除外します
GainとSplit
Gainは、その特徴量が予測精度にどれだけ貢献したかを数値で示したものです。一方Splitは、分岐条件として使われた回数を示します。
今回は、CPU環境でも高速に動作する LightGBM を用いて、上記②~③までを出力するプログラムを作りました。
5 分割のクロスバリデーションを実施し、各分割で得られた結果の平均から特徴量の重要度を算出するようになっています。欠損値は前方補完(forward fill)後に残存欠損を削除することで処理しています。
表示件数(top_n)やクロスバリデーションの分割数(n_splits)は任意に指定可能です。
このグラフと特徴量重要度を出力するプログラムはこちらから入手可能です。
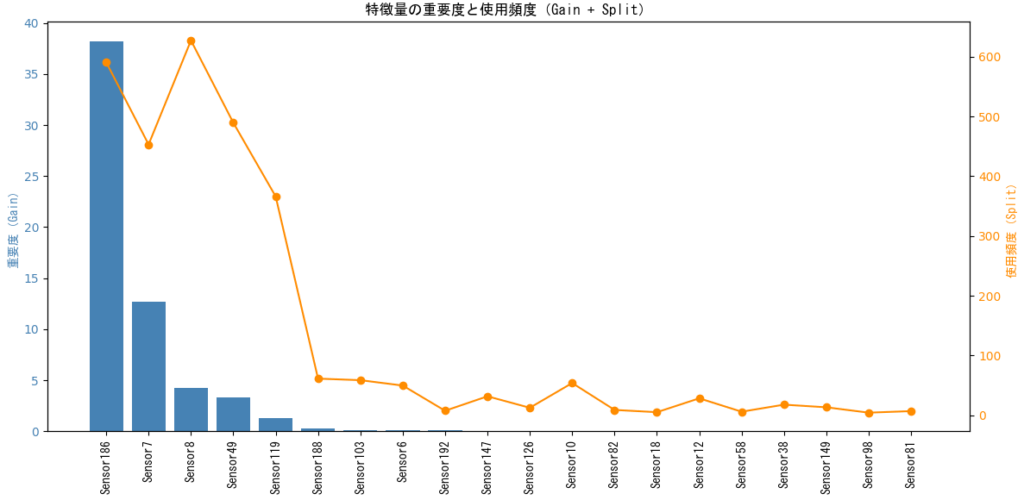
上記グラフでは、各特徴量について以下の2つの指標を同時に可視化しています。
- 青い棒グラフ(左軸):LightGBM による特徴量の重要度(Gain)
→ モデルの誤差を減らすためにどれだけ貢献したかを示します - オレンジの折れ線グラフ(右軸):特徴量の使用頻度(Split)
→ 決定木の分岐に何回使われたかを示します
このように、貢献度と使用頻度を重ねて表示することで、モデルにとって本当に有効な特徴量と、頻繁に使われているが効果が薄い特徴量を識別することができます。
グラフと同時に、GainとSplitの値も出力するようになっています。
平均 R²: 0.9972
平均 MSE: 0.0000
重要度上位 20 特徴量一覧(Gainベース):
1位: Sensor186 → Gain: 38.21, Split: 591
2位: Sensor7 → Gain: 12.71, Split: 453
~~中略~~
19位: Sensor98 → Gain: 0.00, Split: 4
20位: Sensor81 → Gain: 0.00, Split: 7
最後に、この結果から重要度の高い特徴量を選定します。
選定にあたっては、LightGBMが算出した特徴量のGain(分岐による誤差減少の貢献度)を優先し、Split(使用頻度)は補助的に活用します。
Gainが高い特徴量はモデル性能に大きく寄与しているため、優先的に採用します。
一方、Splitはモデルが頻繁に使用した特徴量を示す指標であり、冗長性の判断や補助的な評価に活用します。
| 状況 | 判断と対応 |
|---|---|
| Gain 高↗× Split 高↗ | モデルにとって重要かつ頻繁に使われる → 積極的に採用 |
| Gain 高↗ × Split 低↘ | 少数回の分岐で大きく貢献 → 効率的な特徴量として採用 |
| Gain低↘ × Split 高↗ | 多用されているが貢献度が低い → 冗長の可能性あり、要検討 |
| Gain 低↘ × Split 低↘ | ほとんど使われず貢献も少ない → 除外候補 |
先ほどのグラフの結果から Sensor186とSensor7を評価すると、次のようになります。
Sensor186 の評価
この特徴量は、モデルの予測精度を支える中心的な入力であり、貢献度・使用頻度ともにトップクラス。
除外の余地はなく、今後のモデルでも優先的に採用すべきです。
Gain: 38.21 → モデルの誤差減少に対する貢献度が圧倒的に高い
Split: 591 → 決定木の分岐に最も頻繁に使われている特徴量
Sensor7の評価
Sensor186ほどではないものの、モデルにとって信頼性の高い特徴量。複数の木で繰り返し使われており、予測精度向上に大きく寄与しています。
Gain: 12.71 → 高い貢献度を持つ主要な特徴量
Split: 453 → 使用頻度も非常に高く、安定して分岐に使われている
SHAP値の算出
SHAP(SHapley Additive exPlanations)は、ゲーム理論に基づいて「各特徴量が予測にどれだけ寄与したか」を定量化したものです。
SHAPは本来、モデルが予測した1つの結果(予測値)に対して、どの特徴量がどれくらい関係しているか(ローカル解釈)を調べるためのものですが、データセット全体の予測結果を集計することで、特徴量ごとの重要度(グローバル解釈)を算出することが可能です。
下記の2つのグラフは、SHAP(SHapley Additive exPlanations)による特徴量の寄与分析を「2つの視点」で可視化したものです。左が「個別の寄与」、右が「平均的な寄与の大きさ」です。
- X軸:SHAP値(予測への寄与度)
- 色:特徴量の値(青=低、ピンク=高)
- 点:各サンプルにおけるそのセンサーのSHAP値
個別の寄与

- X軸:SHAP値(予測への寄与度)
- 色:特徴量の値(青=低、ピンク=高)
- 点:各サンプルにおけるそのセンサーのSHAP値
右側に点が多い → 予測を押し上げる方向に寄与
左側に点が多い → 予測を下げる方向に寄与
色が濃いピンクで右側に集中 → 値が高いと予測をし上げる
色が青で左側に集中 → 値が低いと予測を下げる
平均的な寄与の大きさ
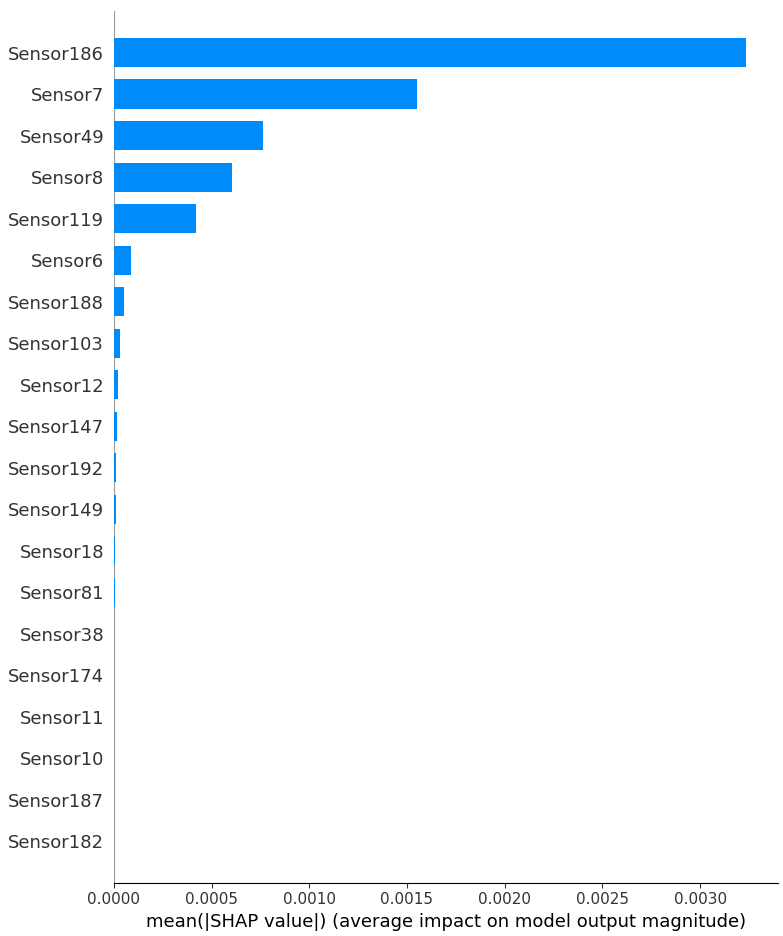
- Y軸:センサー名(特徴量)
- X軸:平均的なSHAP値の絶対値(寄与の大きさ)
棒が長いほど → 予測に強く寄与した特徴量
棒が短いほど → 寄与が小さく、予測にあまり影響していな
[[ 6.29641165e-05 2.25060167e-03 -6.83746022e-04 … 0.00000000e+00
0.00000000e+00 0.00000000e+00]
[ 8.45298998e-05 4.79883457e-03 3.76072747e-03 … 0.00000000e+00
0.00000000e+00 0.00000000e+00]
[ 6.29641165e-05 2.25060167e-03 -6.83747400e-04 … 0.00000000e+00
0.00000000e+00 0.00000000e+00]
…
[ 4.82132532e-05 3.81266322e-03 -1.00692122e-03 … 0.00000000e+00
0.00000000e+00 0.00000000e+00]
[ 4.50578244e-05 4.43059700e-03 -1.09973246e-03 … 0.00000000e+00
0.00000000e+00 0.00000000e+00]
[ 1.04181533e-04 5.37287115e-03 -8.95090768e-04 … 0.00000000e+00
0.00000000e+00 0.00000000e+00]]
SHAPの2つのグラフの関係は次の通り。
| 観点 | SHAP summary plot(散布図) | SHAP bar plot(棒グラフ) |
|---|---|---|
| 目的 | 各サンプルにおける特徴量の寄与方向とばらつきを可視化 | 特徴量ごとの平均的な寄与の大きさを比較 |
| X軸 | SHAP値(予測への寄与度) | 平均SHAP値の絶対値(寄与の強さ) |
| Y軸 | 特徴量(センサー名など) | 特徴量(センサー名など) |
| 色 | 特徴量の値(青=低、ピンク=高) | なし |
| 情報量 | 寄与の方向性・ばらつき・値との関係が分かる | 重要度のランキングが分かる |
| 解釈性 | ローカル(個別予測)の説明に強い | グローバル(全体傾向)の把握に強い |
| 活用例 | なぜその予測になったかを説明する | 重要な特徴量を選定・整理する |
参考プログラム
箱ひげ図・ヒストグラム・散布図・折れ線の描画(特徴量候補の洗い出し)
指定した目的変数と全特徴量について、箱ひげ図・ヒストグラム・散布図・時系列プロットの4種類を1枚にまとめて描画し、除外対象を除いたすべての特徴量に対して、グラフを自動生成して指定フォルダに保存します。
import pandas as pd
import matplotlib.pyplot as plt
import os
import seaborn as sns
def visualize_features_by_column(df, target_col, exclude_cols, save_dir="feature_plots", apply_outlier_filter=False):
"""
df: pandas DataFrame
target_col: 目的変数のカラム名(str)
exclude_cols: 除外対象のカラム名(カンマ区切りのstr)
save_dir: 出力先フォルダ(str)
apply_outlier_filter: 3σ外れ値除外を適用するか(bool)
"""
exclude_list = [col.strip() for col in exclude_cols.split(',')]
feature_cols = [col for col in df.columns if col != target_col and col not in exclude_list]
sns.set_style("whitegrid")
sns.set(font='Meiryo')
os.makedirs(save_dir, exist_ok=True)
for col in feature_cols:
plot_df = df[[col, target_col]].copy()
if apply_outlier_filter:
# 3σで外れ値除外(X軸)
x_mean, x_std = plot_df[col].mean(), plot_df[col].std()
x_mask = (plot_df[col] >= x_mean - 3 * x_std) & (plot_df[col] <= x_mean + 3 * x_std)
# 3σで外れ値除外(Y軸)
y_mean, y_std = plot_df[target_col].mean(), plot_df[target_col].std()
y_mask = (plot_df[target_col] >= y_mean - 3 * y_std) & (plot_df[target_col] <= y_mean + 3 * y_std)
# 両方の条件を満たすデータのみ使用
plot_df = plot_df[x_mask & y_mask]
fig, axes = plt.subplots(1, 4, figsize=(20, 5))
sns.boxplot(y=plot_df[col], ax=axes[0], color='skyblue')
axes[0].set_title(f'Boxplot of {col}')
sns.histplot(plot_df[col], ax=axes[1], bins=20, kde=True, color='mediumseagreen')
axes[1].set_title(f'Histogram of {col}')
sns.scatterplot(x=plot_df[col], y=plot_df[target_col], ax=axes[2], color='salmon')
axes[2].set_title(f'{col} vs {target_col}')
sns.lineplot(x=plot_df.index, y=plot_df[col], ax=axes[3], color='gray')
axes[3].set_title(f'Time Series of {col}')
plt.tight_layout()
filename = os.path.join(save_dir, f"{col}_visualization.png")
fig.savefig(filename)
plt.close(fig)
print(f"Saved: {filename}")
if __name__ == "__main__":
df =pd.read_csv(r"P:\data\sample.csv",encoding="shift-jis")
visualize_features_by_column(df,"Sensor5","Sensor1,Sensor2,Sensor3,Sensor4",r"P:\data\png")説明変数 vs 他の特徴量との散布図(冗長性除外)
目的変数との相関が高いセンサーの上位(top=20)を自動で抽出し、回帰直線付きの散布図を作成して、指定されたフォルダに保存します。各図には相関係数・決定係数(R²)・回帰式がタイトルに表示されます。
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import os
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import numpy as np
sns.set(font='Meiryo', style='whitegrid')
def save_top_scatter_plots_seaborn(df, target_col, exclude_cols, save_dir="scatter_plots", top=10, corr_threshold=0.6):
"""
df: pandas DataFrame
target_col: 目的変数のカラム名(str)
exclude_cols: 除外対象のカラム名(カンマ区切りのstr)
save_dir: 出力先フォルダ(str)
top: 上位から抽出する特徴量数(int)
"""
exclude_list = [col.strip() for col in exclude_cols.split(',')]
feature_cols = [col for col in df.columns if col != target_col and col not in exclude_list]
# 相関係数を目的変数に対して算出(欠損除去後)
correlations = df[feature_cols].corrwith(df[target_col]).sort_values(key=abs, ascending=False)
top_features = correlations[abs(correlations) >= corr_threshold].head(top).index.tolist()
os.makedirs(save_dir, exist_ok=True)
for col in top_features:
subset = df[[col, target_col]].dropna()
total_count = len(subset)
# 元データモデル
x = subset[col].values.reshape(-1, 1)
y = subset[target_col].values
model = LinearRegression().fit(x, y)
y_pred = model.predict(x)
r2 = r2_score(y, y_pred)
coef = model.coef_[0]
intercept = model.intercept_
corr = correlations[col]
# 目的変数(Y)の3σ範囲
mean_y, std_y = subset[target_col].mean(), subset[target_col].std()
lower_y, upper_y = mean_y - 3 * std_y, mean_y + 3 * std_y
mask_y = (subset[target_col] >= lower_y) & (subset[target_col] <= upper_y)
subset_y_filtered = subset[mask_y]
outliers_y = subset[~mask_y]
ratio_y = len(outliers_y) / total_count * 100
# 説明変数(X)の3σ範囲
mean_x, std_x = subset[col].mean(), subset[col].std()
lower_x, upper_x = mean_x - 3 * std_x, mean_x + 3 * std_x
mask_x = (subset[col] >= lower_x) & (subset[col] <= upper_x)
subset_x_filtered = subset[mask_x]
outliers_x = subset[~mask_x]
ratio_x = len(outliers_x) / total_count * 100
# 両方除外
mask_xy = mask_x & mask_y
subset_xy_filtered = subset[mask_xy]
# 中央(Y異常値除外)モデル
x_y = subset_y_filtered[col].values.reshape(-1, 1)
y_y = subset_y_filtered[target_col].values
model_y = LinearRegression().fit(x_y, y_y)
y_pred_y = model_y.predict(x_y)
r2_y = r2_score(y_y, y_pred_y)
coef_y = model_y.coef_[0]
intercept_y = model_y.intercept_
corr_y = subset_y_filtered[col].corr(subset_y_filtered[target_col])
# 右(X異常値除外)モデル
x_x = subset_x_filtered[col].values.reshape(-1, 1)
y_x = subset_x_filtered[target_col].values
model_x = LinearRegression().fit(x_x, y_x)
y_pred_x = model_x.predict(x_x)
r2_x = r2_score(y_x, y_pred_x)
coef_x = model_x.coef_[0]
intercept_x = model_x.intercept_
corr_x = subset_x_filtered[col].corr(subset_x_filtered[target_col])
# 両方除外モデル
x_xy = subset_xy_filtered[col].values.reshape(-1, 1)
y_xy = subset_xy_filtered[target_col].values
model_xy = LinearRegression().fit(x_xy, y_xy)
y_pred_xy = model_xy.predict(x_xy)
r2_xy = r2_score(y_xy, y_pred_xy)
coef_xy = model_xy.coef_[0]
intercept_xy = model_xy.intercept_
corr_xy = subset_xy_filtered[col].corr(subset_xy_filtered[target_col])
# 描画
fig, axes = plt.subplots(1, 4, figsize=(24, 6))
# 左:元データ
sns.scatterplot(x=subset[col], y=subset[target_col], color='salmon', alpha=0.5, ax=axes[0])
sns.scatterplot(x=outliers_y[col], y=outliers_y[target_col], color='red', ax=axes[0], label='Y異常値')
sns.scatterplot(x=outliers_x[col], y=outliers_x[target_col], color='darkred', ax=axes[0], label='X異常値')
sns.lineplot(x=subset[col], y=y_pred, color='blue', ax=axes[0])
axes[0].set_title(
f"元データ\n相関: {corr:.2f}, R²: {r2:.2f}\n回帰: y={coef:.2f}x+{intercept:.2f}\n"
f"Y異常値: {len(outliers_y)}件 ({ratio_y:.1f}%), X異常値: {len(outliers_x)}件 ({ratio_x:.1f}%)",
fontsize=10
)
# 中央:Y異常値除外
sns.scatterplot(x=subset_y_filtered[col], y=subset_y_filtered[target_col], color='green', alpha=0.5, ax=axes[1])
sns.lineplot(x=subset_y_filtered[col], y=y_pred_y, color='blue', ax=axes[1])
axes[1].set_title(
f"目的変数3σ除外\n相関: {corr_y:.2f}, R²: {r2_y:.2f}\n回帰: y={coef_y:.2f}x+{intercept_y:.2f}\n"
f"除外: {len(outliers_y)}件 ({ratio_y:.1f}%), 範囲: [{lower_y:.2f}, {upper_y:.2f}]",
fontsize=10
)
# 右:X異常値除外
sns.scatterplot(x=subset_x_filtered[col], y=subset_x_filtered[target_col], color='purple', alpha=0.5, ax=axes[2])
sns.lineplot(x=subset_x_filtered[col], y=y_pred_x, color='blue', ax=axes[2])
axes[2].set_title(
f"説明変数3σ除外\n相関: {corr_x:.2f}, R²: {r2_x:.2f}\n回帰: y={coef_x:.2f}x+{intercept_x:.2f}\n"
f"除外: {len(outliers_x)}件 ({ratio_x:.1f}%), 範囲: [{lower_x:.2f}, {upper_x:.2f}]",
fontsize=10
)
# 4つ目:両方除外
sns.scatterplot(x=subset_xy_filtered[col], y=subset_xy_filtered[target_col], color='orange', alpha=0.5, ax=axes[3])
sns.lineplot(x=subset_xy_filtered[col], y=y_pred_xy, color='blue', ax=axes[3])
axes[3].set_title(
f"X・Y両方3σ除外\n相関: {corr_xy:.2f}, R²: {r2_xy:.2f}\n回帰: y={coef_xy:.2f}x+{intercept_xy:.2f}\n"
f"除外: Y={len(outliers_y)}件, X={len(outliers_x)}件",
fontsize=10
)
for ax in axes:
ax.set_xlabel(col)
ax.set_ylabel(target_col)
plt.tight_layout()
filename = os.path.join(save_dir, f"{col}_scatter_4views.png")
plt.savefig(filename)
plt.close()
print(f"Saved: {filename}")
if __name__ == "__main__":
df =pd.read_csv(r"P:\data\sample.csv",encoding="shift-jis")
cluster_df = save_top_scatter_plots_seaborn(
df,
target_col="Sensor5",
exclude_cols="Sensor1,Sensor2,Sensor3,Sensor4",
save_dir=r"P:\data\png",
top=10,
)
特徴量のクラスタリング(冗長性除外)
目的変数との相関が高い特徴量を上位20個選び、それらをクラスタリングして「似た特徴量群」を可視化します。
各特徴量の冗長性(VIF)も併せて表示し、クラスタごとに代表的な特徴量を選ぶ判断材料を提供します。
結果はグラフとして保存され、クラスタ情報が戻り値として返されます。
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import os
from sklearn.cluster import AgglomerativeClustering
from sklearn.preprocessing import StandardScaler
from statsmodels.stats.outliers_influence import variance_inflation_factor
plt.rcParams['font.family'] = 'Meiryo'
sns.set(font='Meiryo', style='whitegrid')
def analyze_feature_redundancy(df, target_col, exclude_cols, top=20, n_clusters=5, save_path="feature_redundancy.png"):
"""
df: pandas DataFrame
target_col: 目的変数のカラム名(str)
exclude_cols: 除外対象のカラム名(カンマ区切りのstr)
top: 相関上位の特徴量数(int)
n_clusters: クラスタ数(int)
save_path: 可視化の保存先(str)
"""
exclude_list = [col.strip() for col in exclude_cols.split(',')]
feature_cols = [col for col in df.columns if col != target_col and col not in exclude_list]
# 相関係数で上位特徴量を抽出
correlations = df[feature_cols].corrwith(df[target_col]).sort_values(key=abs, ascending=False)
top_features = correlations.head(top).index.tolist()
# 欠損と定数列を除去
subset = df[top_features].dropna()
subset = subset.loc[:, subset.std() != 0]
# 相関行列 → 距離行列
corr_matrix = subset.corr().abs()
distance_matrix = 1 - corr_matrix
# クラスタリング
clustering = AgglomerativeClustering(n_clusters=n_clusters, metric='precomputed', linkage='average')
labels = clustering.fit_predict(distance_matrix)
# VIF計算
scaled = StandardScaler().fit_transform(subset)
vif_values = [variance_inflation_factor(scaled, i) for i in range(scaled.shape[1])]
# 結果まとめ
result_df = pd.DataFrame({
'feature': subset.columns,
'correlation': correlations[subset.columns].values,
'cluster': labels,
'VIF': vif_values
}).sort_values(by='cluster')
# 可視化
plt.figure(figsize=(10, 6))
sns.scatterplot(data=result_df, x='feature', y='correlation', hue='cluster', size='VIF',
palette='tab10', sizes=(50, 300), legend='brief')
plt.xticks(rotation=45, ha='right')
plt.title(f"{target_col} に対する特徴量の冗長性分析", font='Meiryo')
plt.tight_layout()
os.makedirs(os.path.dirname(save_path), exist_ok=True)
plt.savefig(save_path)
plt.close()
print(f"Saved: {save_path}")
return result_df
if __name__ == "__main__":
df = pd.read_csv(r"P:\data\sample.csv", encoding="shift-jis")
redundancy_df = analyze_feature_redundancy(
df,
target_col="Sensor1",
exclude_cols="Sensor1,Sensor2,Sensor3,Sensor4",
top=20,
n_clusters=5,
save_path=r"P:\data\feature_redundancy.png"
)
# クラスタごとの代表特徴量を確認
print(redundancy_df.groupby('cluster').first())LightGBM による特徴量選定
このプログラムは、LightGBM を用いて回帰モデルを学習し、K 分割のクロスバリデーションにより予測精度(R²・MSE)と特徴量の平均重要度を算出します。
欠損値は前方補完(forward fill)を行った後、補完できなかった行を削除することで処理されます。
学習後、特徴量の重要度を Gain(分岐貢献度)と Split(使用頻度)の両指標で評価し、上位 N 件をコンソールとグラフで可視化します。
表示件数(top_n)やクロスバリデーションの分割数(n_splits)は任意に指定可能です。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from lightgbm import LGBMRegressor
from sklearn.model_selection import KFold
from sklearn.metrics import mean_squared_error, r2_score
class GBDTFeatureEvaluator:
def __init__(self, df: pd.DataFrame, target_col: str, exclude_cols: str = "", test_size: float = 0.2, random_state: int = 42):
"""
クラスの初期化:データと設定を受け取り、LightGBMモデルを準備します。
Parameters:
df (pd.DataFrame): 入力データフレーム
target_col (str): 予測対象となる目的変数の列名
exclude_cols (str): モデルに使わない列名(カンマ区切りで指定)
test_size (float): 検証データの割合(未使用:CVで分割するため)
random_state (int): 乱数シード(再現性確保のため)
"""
self.df = df.copy()
self.target_col = target_col
self.exclude_cols = [col.strip() for col in exclude_cols.split(",") if col.strip()]
self.test_size = test_size
self.random_state = random_state
self.model = LGBMRegressor(random_state=self.random_state)
self.boosters = [] # 各foldのboosterを保存(Gain取得用)
def prepare_data(self):
"""
特徴量と目的変数に分割し、除外列を取り除きます。
"""
drop_cols = self.exclude_cols + [self.target_col]
self.X = self.df.drop(columns=drop_cols, errors="ignore")
self.y = self.df[self.target_col]
def train_model(self, n_splits: int = 5):
"""
K分割交差検証でLightGBMモデルを学習し、平均スコアと特徴量重要度(Gain/Split)を算出します。
Parameters:
n_splits (int): クロスバリデーションの分割数(fold数)
"""
kf = KFold(n_splits=n_splits, shuffle=True, random_state=self.random_state)
r2_scores = []
mse_scores = []
self.feature_importances_split = np.zeros(self.X.shape[1]) # 使用頻度(Split)
self.feature_importances_gain = np.zeros(self.X.shape[1]) # 分岐貢献度(Gain)
for fold, (train_idx, val_idx) in enumerate(kf.split(self.X), 1):
# 学習・検証データに分割
X_train, X_val = self.X.iloc[train_idx], self.X.iloc[val_idx]
y_train, y_val = self.y.iloc[train_idx], self.y.iloc[val_idx]
# 欠損値処理:前方補完 → 補完できなかった行を削除
X_train = X_train.fillna(method='ffill').dropna()
y_train = y_train.loc[X_train.index]
X_val = X_val.fillna(method='ffill').dropna()
y_val = y_val.loc[X_val.index]
# モデル学習
model = LGBMRegressor(random_state=self.random_state)
model.fit(X_train, y_train)
# 検証データで予測・評価
y_pred = model.predict(X_val)
r2_scores.append(r2_score(y_val, y_pred))
mse_scores.append(mean_squared_error(y_val, y_pred))
# Boosterオブジェクトを保存(Gain取得用)
booster = model.booster_
self.boosters.append(booster)
# 特徴量重要度を加算(後で平均化)
self.feature_importances_split += booster.feature_importance(importance_type='split')
self.feature_importances_gain += booster.feature_importance(importance_type='gain')
print(f"[Fold {fold}] R²: {r2_scores[-1]:.4f}, MSE: {mse_scores[-1]:.4f}")
# 平均スコアと重要度を出力
print(f"\n平均 R²: {np.mean(r2_scores):.4f}")
print(f"平均 MSE: {np.mean(mse_scores):.4f}")
self.feature_importances_split /= n_splits
self.feature_importances_gain /= n_splits
def plot_feature_importance(self, top_n: int = 20):
features = self.boosters[0].feature_name()
indices = np.argsort(self.feature_importances_gain)[::-1][:top_n]
gain_values = self.feature_importances_gain[indices]
split_values = self.feature_importances_split[indices]
feature_names = [features[i] for i in indices]
# コンソール出力
print(f"\n重要度上位 {top_n} 特徴量一覧(Gainベース):")
for i, idx in enumerate(indices):
print(f"{i+1:2d}位: {features[idx]:<20} → Gain: {self.feature_importances_gain[idx]:.2f}, Split: {self.feature_importances_split[idx]:.0f}")
# グラフ描画(棒グラフ+折れ線グラフ)
fig, ax1 = plt.subplots(figsize=(12, 6))
ax1.bar(feature_names, gain_values, color='steelblue', label='Gain')
ax1.set_ylabel('重要度(Gain)', fontname='MS Gothic', color='steelblue')
ax1.tick_params(axis='y', labelcolor='steelblue')
ax1.set_xticklabels(feature_names, rotation=90, fontname='MS Gothic')
ax1.set_title('特徴量の重要度と使用頻度(Gain + Split)', fontname='MS Gothic')
# 第2軸(Split)
ax2 = ax1.twinx()
ax2.plot(feature_names, split_values, color='darkorange', marker='o', label='Split')
ax2.set_ylabel('使用頻度(Split)', fontname='MS Gothic', color='darkorange')
ax2.tick_params(axis='y', labelcolor='darkorange')
fig.tight_layout()
plt.show()
def run(self, n_splits: int = 5, top_n: int = 20):
"""
一連の処理を実行:データ準備 → モデル学習 → 重要度可視化
Parameters:
n_splits (int): クロスバリデーションの分割数
top_n (int): 表示する特徴量の上位件数
"""
self.prepare_data()
self.train_model(n_splits=n_splits)
self.plot_feature_importance(top_n=top_n)
if __name__ == "__main__":
df = pd.read_csv(r"P:\data\sample.csv", encoding="shift-jis")
evaluator = GBDTFeatureEvaluator(
df=df,
target_col="Sensor5",
exclude_cols="Sensor1,Sensor2,Sensor3,Sensor4"
)
evaluator.run(n_splits=5, top_n=20)
SHAP値
このプログラムは、LightGBM を用いて分類または回帰モデルを自動判定し学習し、SHAP により各特徴量の寄与度を算出・可視化します。
入力データから目的変数列と除外列を指定することで、残りの特徴量をモデルに利用します。
学習後、SHAP の summary plot(散布図)により「特徴量の値が予測を押し上げるか下げるか」を可視化し、bar plot(棒グラフ)により「平均的な寄与度の大きさ」をランキング形式で表示します。
これにより、予測対象に対してどの特徴量が強く影響しているかを直感的に理解でき、モデル解釈や特徴量選定に活用できます。
import pandas as pd
import lightgbm as lgb
import shap
import matplotlib.pyplot as plt
# pip install shap
def show_shap_values(df: pd.DataFrame, target_col: str, exclude_cols: str = ""):
"""
SHAP値を算出し、summary plot と bar plot を表示する関数
Parameters
----------
df : pd.DataFrame
入力データフレーム
target_col : str
予測対象となる目的変数の列名
exclude_cols : str
モデルに使わない列名(カンマ区切り)
"""
# 除外列をリスト化
exclude_list = [c.strip() for c in exclude_cols.split(",") if c.strip()]
# 特徴量と目的変数を分離
X = df.drop(columns=[target_col] + exclude_list)
y = df[target_col]
# LightGBMモデルを学習(分類/回帰を自動判定)
if y.nunique() <= 10 and y.dtype in [int, "int64", "int32"]:
model = lgb.LGBMClassifier()
else:
model = lgb.LGBMRegressor()
model.fit(X, y)
# SHAP値を算出
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(X)
# グローバル解釈(summary plot)
shap.summary_plot(shap_values, X)
# バー表示(平均寄与度)
shap.summary_plot(shap_values, X, plot_type="bar")
return shap_values
if __name__ == "__main__":
# CSVファイルの読み込み(Shift-JISエンコーディング)
df = pd.read_csv(r"P:\data\sample.csv", encoding="shift-jis")
# 評価器の初期化と実行
res = evaluator = show_shap_values(
df=df,
target_col="Sensor5", # 予測対象のセンサー値
exclude_cols="Sensor1,Sensor2,Sensor3,Sensor4" # 除外するセンサー列
)
print(res)
まとめ
アンサンブル回帰モデルにおける特徴量選定は、単なる相関分析では捉えきれない「非線形性」「冗長性」「安定性」「多様性」といった複雑な要素を見極めるプロセスです。
本記事では、大量データを前提とした実践的な選定手順を、以下の4ステップに分けて体系的に整理しました。
- 軽量化:統計サマリやピーク抽出などで、時系列の本質を保ちながらデータを圧縮
- 候補選定:箱ひげ図・ヒストグラム・散布図・折れ線グラフを用いた視覚的スクリーニング
- 冗長性除去:相関・クラスタ・VIFを組み合わせて、似た特徴量群から代表を選定
- 重要度評価:LightGBMによる非線形な予測貢献度の定量評価と最終選定
特徴量選定は、モデル構築の前処理ではなく、予測性能と運用品質を左右する需要な工程です。
本記事が、大量データを用いたアンサンブル回帰モデルの特徴量選定の参考になれば幸いです。









コメント