場やプラントの設備は、止まってしまえば生産性や安全性に直結する重要な存在です。
しかし、故障や不具合は突然起こるのではなく、必ず小さな「予兆」を伴っています。振動、温度、電流、圧力――日々収集されるセンサーデータの中に、その兆しは隠れています。
設備の異常検知とは、この予兆をいち早く捉え、計画的なメンテナンスやダウンタイム削減につなげる技術です。統計的手法から機械学習、ディープラーニングまで多様なアプローチがあり、振幅や周波数、周期性などの変化を分析することで、故障の芽を事前に摘み取ることが可能になります。
本記事では、異常検知の基本的な考え方から代表的な手法、そして設備データに現れる典型的な異常パターンを整理し、わかりやすく解説します。
設備の異常検知とは
設備の異常検知とは、機械や装置が通常とは異なる挙動を示した際に、その兆候を早期に捉える技術のことです。工場やプラントでは、振動・温度・電流・圧力など多様なセンサーデータが常時収集されています。これらのデータを解析することで、故障や不具合が顕在化する前に「予兆」を検知し、計画的なメンテナンスやダウンタイム削減につなげることができます。
異常検知を行うことで、次のようなメリットがあります。
- 予防保全:突発的な故障を防ぎ、計画的なメンテナンスを可能にする
- 生産性向上:設備停止による損失を最小化し、稼働率を高める
- 安全性確保:異常を早期に発見することで事故や品質トラブルを防止
- コスト削減:不要な部品交換や過剰な点検を減らし、効率的な運用を実現
異常検知の主なアプローチ
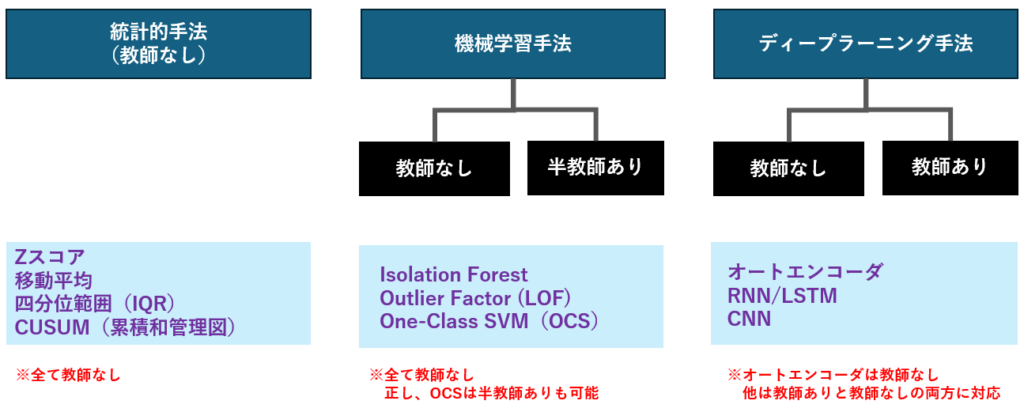
異常検知は大きく分けると 統計的手法・機械学習手法・ディープラーニング手法 の3つに分類できます。さらに、これらの手法は「教師あり(ラベル付きデータを用いる)」と「教師なし(正常データや分布のみを用いる)」の2つのパターンに分けられます。設備異常検知の現場では、異常データが少ないため教師なし手法が中心となりますが、ラベル付きデータが豊富にある場合には教師あり手法が高い精度を発揮します。それぞれの特徴を整理すると以下の通りです。
統計的手法(教師なし)
もっとも古典的でシンプルな方法です。平均値や分散を基準に「通常範囲」を定義し、その範囲から外れた値を異常とみなします。代表的な手法には Zスコア、移動平均、IQR、CUSUM などがあり、計算が軽いためリアルタイム監視に適しています。ただし、複雑なパターンや多変量データには対応が難しいという弱点があります。
- 考え方:データの平均値や分散を基準に「通常範囲」を定義し、その範囲から外れた値を異常とみなす。
- 代表例:Zスコア、移動平均、四分位範囲(IQR)、CUSUM(累積和管理図)など。
- メリット:計算が軽く、リアルタイム監視に向いている。
- デメリット:複雑なパターンや多変量データには対応が難しい。
機械学習手法(主に教師なし/半教師あり)
統計的手法より柔軟で、複雑なデータ構造にも対応できるアプローチです。正常データの分布や構造を学習し、それから外れるデータを異常と判定します。代表例は Isolation Forest(孤立しやすい点を異常と判定)、LOF(局所密度比による異常検出)、One-Class SVM(正常境界を学習し外側を異常と判定)など。多次元データや複雑なパターンに強い一方で、パラメータ調整やラベル付きデータが必要になる場合があります。
- 考え方:正常データの分布や構造を学習し、それから外れるデータを異常と判定する。
- 代表例:
- Isolation Forest:ランダム分割で孤立しやすい点を異常とみなす。大規模データに強い。
- Local Outlier Factor (LOF):近傍点との密度比を利用して異常を検出。局所的な異常に強い。
- One-Class SVM:正常データの境界を学習し、外側を異常と判定。非線形データにも対応可能。
- メリット:多次元データや複雑なパターンを扱える。
- デメリット:パラメータ調整が必要で、ラベル付きデータがあると精度が上がる。
ディープラーニング手法(教師なし/教師あり)
近年注目されている最先端のアプローチです。ニューラルネットワークを使い、正常データを再構築した際の誤差や予測誤差を監視することで異常を検出します。代表例はオートエンコーダ(再構築誤差)、RNN/LSTM(時系列予測誤差)、CNN(画像や波形データの異常検知)など。複雑な非線形パターンや高次元データに強く、特徴量設計を自動化できる点が魅力ですが、大量のデータと計算資源が必要で、モデル解釈性が低いという課題もあります。
- 考え方:ニューラルネットワークを使い、正常データを再構築した際の誤差を監視することで異常を検出。
- 代表例:
- オートエンコーダ:入力データを圧縮・再構築し、誤差が大きいものを異常と判定。
- RNN/LSTM:時系列データの予測誤差を利用して異常を検出。
- CNN:画像や波形データの異常検知に強い。
- メリット:複雑な非線形パターンや高次元データに強く、特徴量設計を自動化できる。
- デメリット:大量のデータと計算資源が必要で、モデル解釈性が低い。
異常検知の手順
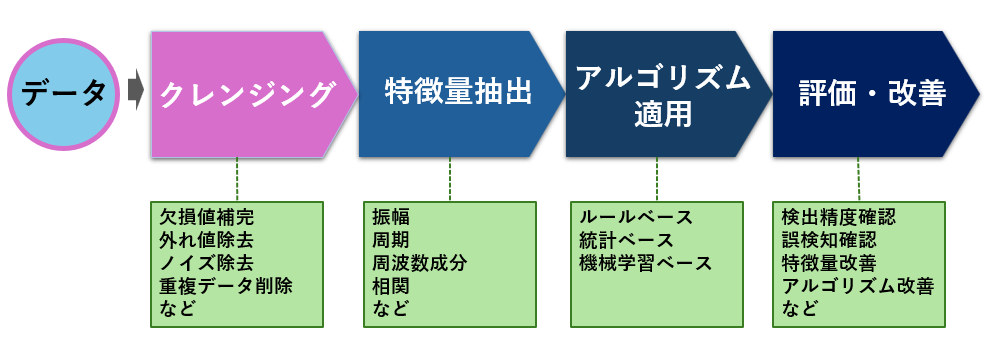
一般的な異常検知の手順は「データの準備(クレンジング)→特徴量設計→検出アルゴリズム適用→評価・改善」という流れです。特に最初のクレンジング工程が精度を大きく左右します。
クレンジング
クレンジング(データクレンジング)とは、分析や機械学習に使う前に、データの質を整えるための前処理のことです。 正確で信頼性の高いデータを得るために、以下のような処理を行います。
- 重複データの削除:同じ内容の行を取り除き、集計や学習の偏りを防ぎます。
- 欠損値の処理:不足しているデータを削除または補完し、分析や学習の安定性を確保します。
- 異常値の処理:極端な値を検出して除外または補正し、統計やモデルへの悪影響を防ぎます。
- データのスケーリング:特徴量の値を共通のスケールに整え、学習効率と精度を向上させます。
- カテゴリーデータのエンコード:文字列などのカテゴリ情報を数値に変換し、機械学習で扱える形式にします。
より詳しい内容については、下記の記事にまとめていますので、併せてご覧ください。

スライディングウィンドウを用いた特徴量抽出
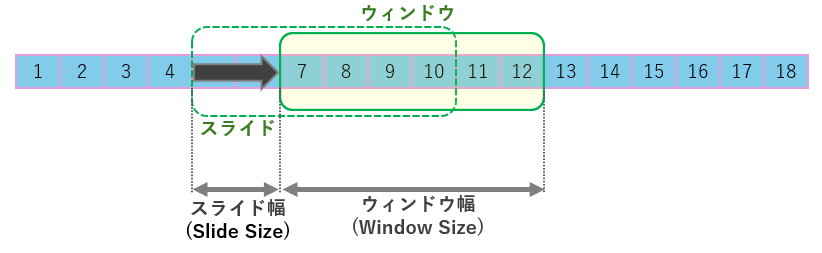
異常は多くの場合、短時間の局所的な変化として現れます。
そのため、異常検知ではスライディングウィンドウを用いて特徴量を計算し、それをモデルに投入する方法が一般的です。
全データをそのまま扱うよりも、局所的な変化を捉えやすく、計算効率や汎化性能の面でも有利になります。
ウィンドウサイズは「どれくらいの時間・データ範囲で特徴量を計算するか」を決めるパラメータです。
信号の周期性:1周期〜数周期を含むサイズが望ましい
→ 例:周期が約1秒なら、ウィンドウサイズは1〜3秒程度
異常の持続時間:異常が現れる時間スケールに合わせる
→ 瞬間的なスパイクなら短め、徐々に変化する異常なら長め
サンプリングレート:1秒あたりのデータ数に応じて調整
→ 例:100Hzなら1秒=100データ → ウィンドウサイズ100が1秒分
スライドサイズは「ウィンドウをどれだけずらして次の特徴量を計算するか」を決めるパラメータです。
検出の滑らかさ vs 計算効率のトレードオフ
ウィンドウサイズの10〜50%程度が一般的
→ ウィンドウサイズ100なら、スライドサイズ10〜50

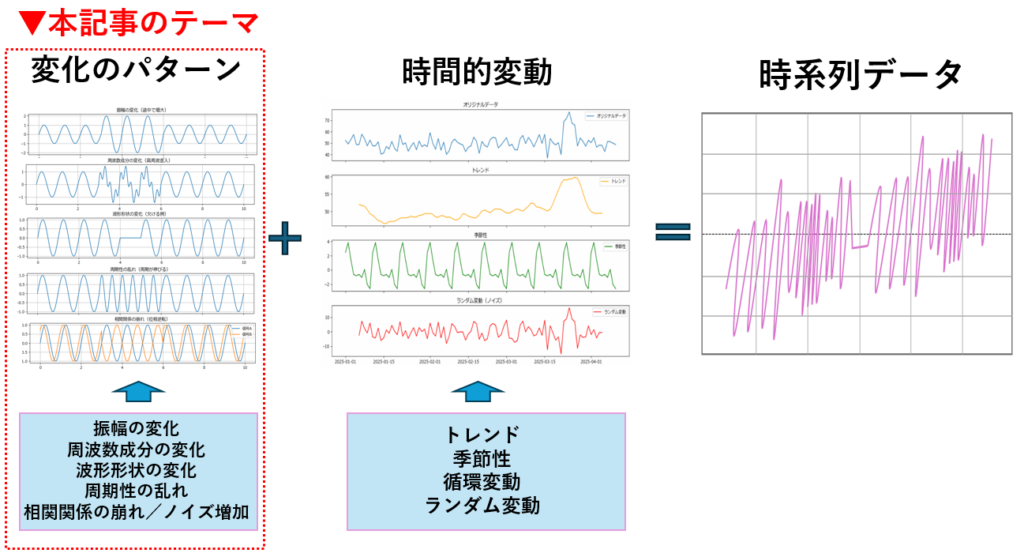
代表的な5つの異常パターンと検出手法
設備データに現れる異常にはいくつかの典型的なパターンがあります。これらを理解しておくことで、現場でのトラブルを早期に察知し、適切な検出手法を選択することが可能になります。ここでは、設備異常を捉える上で特に重要な5つのパターンを整理し、それぞれに対応する代表的な検出手法を一覧にまとめました。
| パターン名 | 説明 | 代表的な検出手法 |
|---|---|---|
| 振幅の変化 | 信号や振動の大きさが通常より増加・減少する異常。 | 統計的閾値判定(Zスコア、IQR、CUSUMなど)+平滑化手法(移動平均、指数平滑化など)を組み合わせて使用 |
| 周波数成分の変化 | FFTなどのスペクトル解析で新しいピークが出現、既存ピークが強調される。 | FFT解析、ウェーブレット変換+機械学習(One-Class SVM、ランダムフォレスト、決定木、Isolation Forestなど) |
| 波形形状の変化 | 信号の形が尖る、歪む、非対称になるなど通常と異なる波形になる。 | オートエンコーダによる再構築誤差、DTW(動的時間伸縮法)、CNN |
| 周期性の乱れ | 本来一定周期で繰り返されるパターンが不安定になる。 | 自己相関解析、ARモデル/ARIMA/SARIMA/Prophetによる予測残差分析、RNN/LSTMよる時系列予測と異常スコア算出 |
| 相関関係の崩れ/ノイズ増加 | 複数センサ間の関係が弱まる・逆転する、またはノイズレベルが増加する。 | PCA残差分析、マハラノビス距離、相関係数監視、グラフニューラルネットワーク |
信号の平均値が時間とともに持続的に上昇・下降する「トレンド変化(レベルシフト/ドリフト)」も現場で頻出する異常です。これは振幅の変化の一種として扱われることが多く、移動平均やCUSUMなどの統計的手法で検出されます。
パターン1.振幅の変化
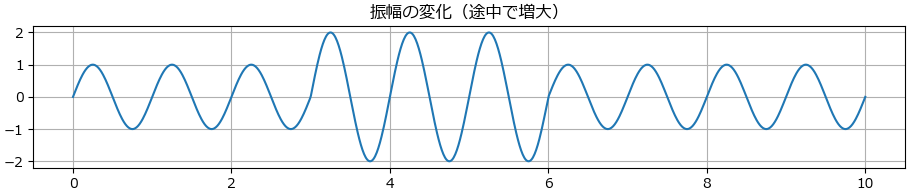
振幅の変化とは、時系列信号において波形の高さ(ピーク値)が一時的または継続的に増減する現象を指します。通常、信号の振幅は安定していることが多いですが、異常や外乱が加わることで、振幅が急激に大きくなったり小さくなったりすることがあります。
このような変化は、機械の動作状態や外部環境の変化を反映している可能性があり、異常検知や予兆保全の観点から重要な指標となります。
振幅が変化する理由
振幅の変化が生じる原因として、以下のようなものが考えられます。
- 負荷の急変:モーターやポンプなどが急に重い負荷を受けた場合、振幅が増大することがある
- センサの劣化やノイズ混入:センサの感度が変化したり、外部ノイズが混入することで振幅が不安定になる
- 物理的衝撃や振動:機械的な衝突や振動が加わることで、一時的に振幅が跳ね上がる
- 制御系の異常:フィードバック制御が不安定になると、振幅が周期的に増減することがある
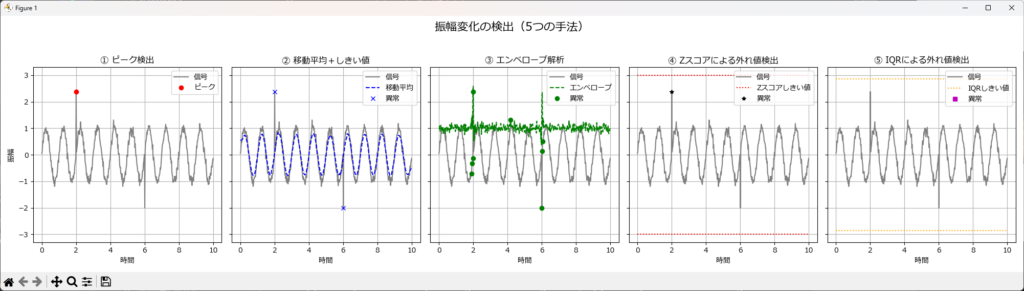
検出手法
振幅の変化を検出するためには、以下のような手法が有効です。
- ピーク検出アルゴリズム:局所的な最大値・最小値を抽出し、振幅の変化を定量化
- 移動平均+しきい値判定:振幅の平均値を滑らかに追跡し、一定のしきい値を超えたら異常と判定
- エンベロープ解析:信号の包絡線を抽出し、振幅の変動を時間的に追跡
- 統計的手法(Zスコア、IQRなど):振幅の分布から外れ値を検出
よく使われる特徴量
振幅の変化を定量的に捉えるために、以下のような特徴量がよく使われます。
- 振幅レンジ(Max - Min)
最大値と最小値の差を取ったものです。振幅の変動幅を定量化でき、安定性の指標として使われます。 - RMS(Root Mean Square)
振幅の二乗平均平方根で、信号の平均的なエネルギー量を表します。ノイズや振動の強さを反映するため、機械の健全性評価に適しています。 - エンベロープ平均
信号の包絡線を抽出し、その平均値を計算します。振幅のトレンドを追跡するのに適しており、徐々に増大する異常を検出できます。 - 振幅の標準偏差
振幅のばらつきを表す指標です。安定した信号では小さく、異常や外乱があると大きくなるため、変動の検出に有効です。
パターン2.周波数成分の変化
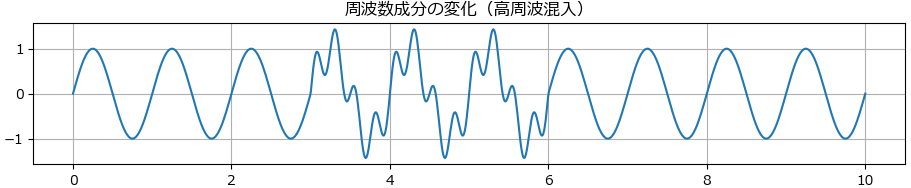
周波数成分の変化とは、時系列信号において波形を構成する周波数の構造が一時的または継続的に変化する現象を指します。通常、信号は特定の基本周波数やその高調波で構成されますが、異常や外乱が加わることで新しい周波数成分が混入したり、既存の周波数が強調・減衰したりすることがあります。
このような変化は、機械の動作状態や外部環境の変化を反映している可能性があり、スペクトル解析や異常検知の観点から重要な指標となります。
周波数成分が変化する理由
周波数成分の変化が生じる原因として、以下のようなものが考えられます。
- 負荷の変動:モーターや回転機械の回転数が変化すると、基本周波数が変わる
- 共振や構造変化:機械部品の摩耗や破損により、新しい共振周波数が現れる
- 外部ノイズの混入:電気的ノイズや環境振動が加わり、異なる周波数成分が混ざる
- 制御系の不安定化:制御ループの乱れにより、周期的な高周波成分が発生する
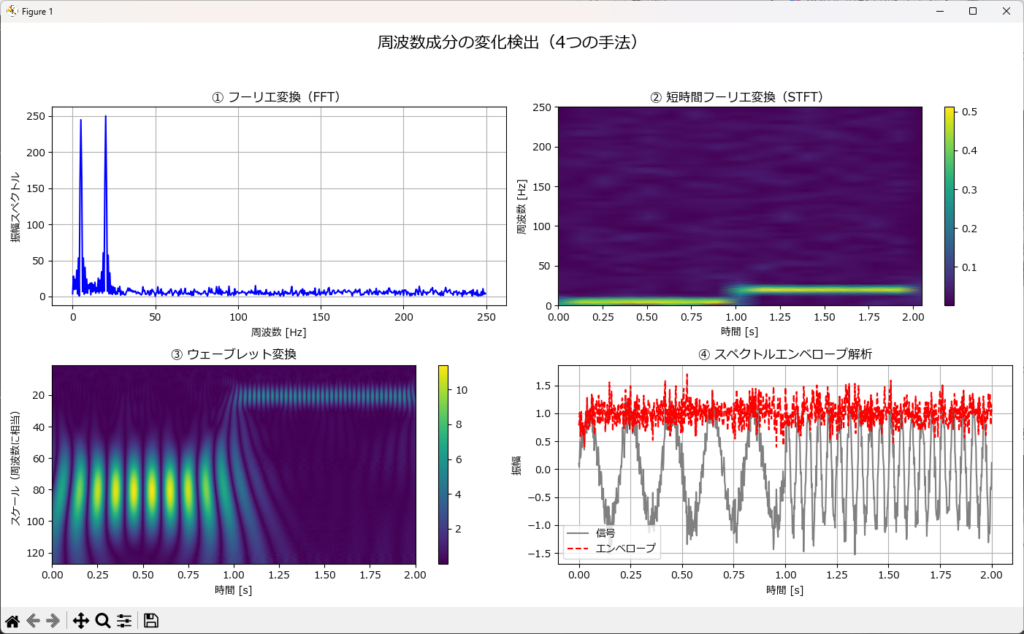
検出手法
周波数成分の変化を検出するためには、以下のような手法が有効です。
- フーリエ変換(FFT):信号を周波数領域に変換し、スペクトルのピーク変化を観察
- 短時間フーリエ変換(STFT):時間ごとの周波数成分を追跡し、変化を時系列で捉える
- ウェーブレット変換:非定常信号に対して周波数変化を多解像度で解析
- スペクトルエンベロープ解析:周波数成分の包絡線を抽出し、成分の増減を追跡
これらはいずれも、周波数スペクトルにおけるピークの位置や強さの変化に着目した手法です。 一方で、もうひとつの視点として、側波帯(中心ピークの“周辺”に現れる微弱な周波数成分)の揺らぎに注目し、そこから異常を検知する方法もあります。
側波帯は、信号の変調や周期性の乱れによって現れる“周波数の影”のような存在で、通常のスペクトル解析では見逃されがちな異常の兆候を捉えるのに有効です。

よく使われる特徴量
周波数成分の変化を定量的に捉えるために、以下のような特徴量がよく使われます。
- 主成分周波数(Dominant Frequency)
スペクトルの中で最も強いピークを持つ周波数。基本動作の変化を検出するのに有効。 - 周波数帯域エネルギー(Band Energy)
特定の周波数帯域に含まれるエネルギー量。ノイズや共振の影響を評価できる。 - スペクトル重心(Spectral Centroid)
周波数分布の重心を表す指標。高周波成分が増えると値が大きくなる。 - スペクトル拡がり(Spectral Spread)
周波数分布の広がりを示す。安定した信号では狭く、異常時には広がる。 - 周波数成分の標準偏差
周波数ピークのばらつきを表す。安定性の指標として使える。
パターン3.波形形状の変化
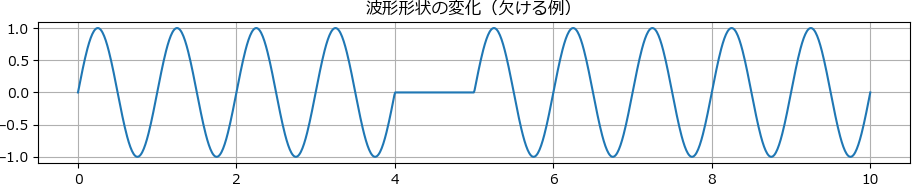
波形形状の変化とは、時系列信号において波形の形そのものが一時的または継続的に歪んだり欠けたりする現象を指します。通常、信号は滑らかな正弦波や安定したパターンを示しますが、異常や外乱が加わることで波形が部分的に潰れたり、尖ったピークが現れたり、あるいは一部が欠落することがあります。
このような変化は、機械の物理的状態やセンサの異常を直接反映している可能性があり、異常検知や品質管理の観点から重要な指標となります。
波形形状が変化する理由
波形形状の変化が生じる原因として、以下のようなものが考えられます。
- センサの欠陥や応答不良:一部の波形が欠ける、途切れる
- 機械的摩耗や衝撃:ピークが潰れる、山が平らになる
- 外部ノイズや突発的イベント:一部に尖ったスパイクが混入する
- 制御系の異常:波形が非対称になったり、周期ごとに形が変わる
検出手法
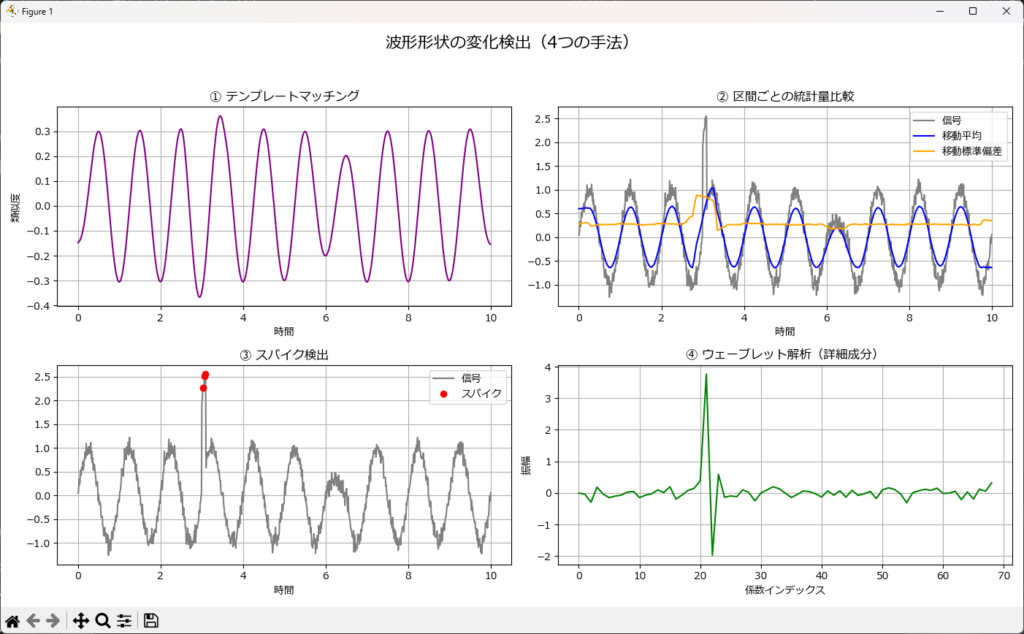
波形形状の変化を検出するためには、以下のような手法が有効です。
- 波形テンプレートマッチング:正常波形と比較し、形状の差異を検出
- 区間ごとの統計量比較:部分区間の平均値や分散を比較し、異常を抽出
- スパイク検出アルゴリズム:急激なピークや欠落を検出
- ウェーブレット解析:局所的な形状変化を多解像度で捉える
よく使われる特徴量
波形形状の変化を定量的に捉えるために、以下のような特徴量がよく使われます。
- 波形対称性(Symmetry)
波形が左右対称かどうかを評価。非対称になると異常の可能性が高い。 - 波形尖度(Kurtosis)
波形の尖り具合を表す指標。スパイクや異常ピークの検出に有効。 - 波形歪度(Skewness)
波形の非対称性を定量化。偏りが大きいと異常を示す。 - 区間欠落率(Missing Ratio)
信号の一部が欠けている割合。センサ不良や途切れの検出に使われる。 - 局所的標準偏差
区間ごとのばらつきを評価。正常波形では安定、異常波形では急増する。
パターン4.周期性の乱れ
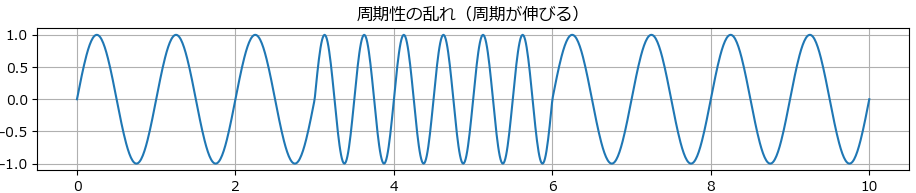
周期性の乱れとは、時系列信号において波形の繰り返し周期が一時的または継続的に変化する現象を指します。通常、信号は一定の周期で繰り返されますが、異常や外乱が加わることで周期が伸びたり縮んだり、あるいは不規則に揺らぐことがあります。
このような変化は、機械の運転状態や外部環境の影響を反映している可能性があり、異常検知や予兆保全の観点から重要な指標となります。
周期性が乱れる理由
周期性の乱れが生じる原因として、以下のようなものが考えられます。
- 回転数の変動:モーターや回転機械の速度が不安定になることで周期が変化する
- 摩耗や劣化:部品の摩耗により動作リズムが乱れる
- 外部衝撃や負荷変動:周期的な動作に外乱が加わり、一部の周期が伸縮する
- 制御系の不安定化:フィードバック制御が乱れることで周期が揺らぐ
検出手法
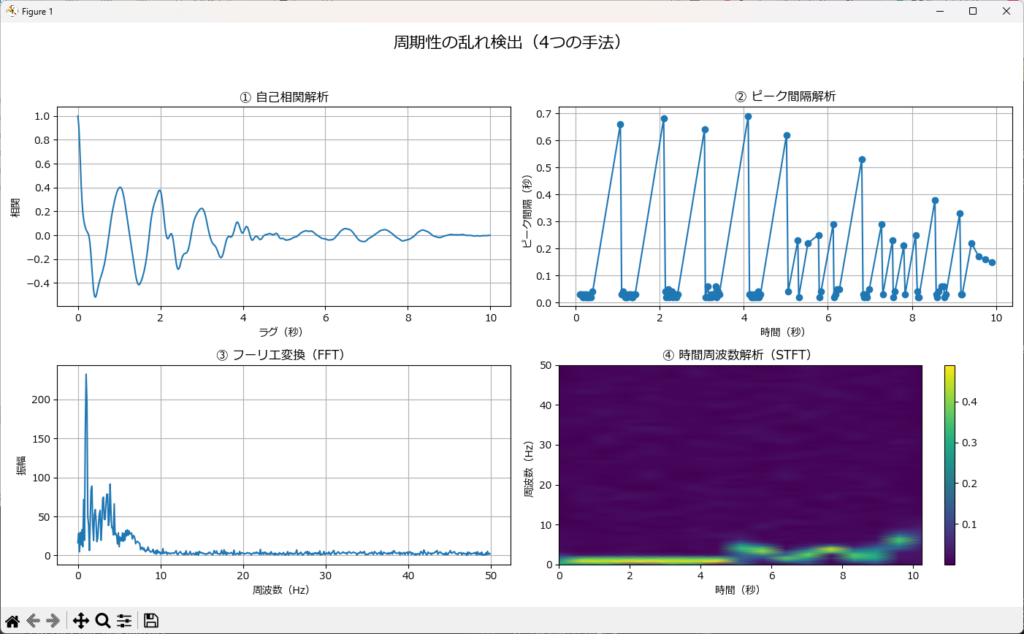
周期性の乱れを検出するためには、以下のような手法が有効です。
- 自己相関解析:信号の周期性を評価し、乱れを検出
- ピーク間隔解析:波形のピーク間隔を計測し、周期の伸縮を定量化
- スペクトル解析(FFT):基本周波数の変動やピークの広がりを確認
- 時間周波数解析(STFT、ウェーブレット):周期の揺らぎを時間的に追跡
- 予測モデルによる残差分析: ARIMA、SARIMA、Prophet、RNN、LSTMなどの時系列予測モデルを用いて将来の値を予測し、実測値との差(残差)から周期性の乱れを検出。
よく使われる特徴量
周期性の乱れを定量的に捉えるために、以下のような特徴量がよく使われます。
- 平均周期(Mean Period)
ピーク間隔の平均値。周期の基準を示す。 - 周期の標準偏差(Period Std)
ピーク間隔のばらつきを表す。周期が安定していれば小さく、乱れると大きくなる。 - 基本周波数の変動幅(Frequency Variation)
FFTで得られる基本周波数の変動量。周期の揺らぎを反映する。 - 周期安定度指数(Stability Index)
周期の一貫性を数値化した指標。安定性評価に用いられる。 - スペクトルピーク幅(Peak Bandwidth)
周波数ピークの広がりを表す。周期が乱れると広がりが大きくなる。
パターン5.相関関係の崩れ(またはノイズ増加)
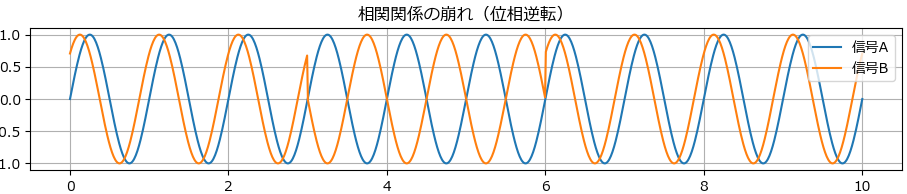
相関関係の崩れとは、複数の時系列信号の間に存在していた一定の関係性(同期や位相の一致)が失われる現象を指します。通常、関連するセンサや機械部品の信号は強い相関を持ちますが、異常や外乱が加わることで相関が弱まり、逆相関や不規則な関係に変化することがあります。また、ノイズが増加すると信号間の関係が曖昧になり、相関が崩れたように見える場合もあります。
このような変化は、システム全体の協調動作が乱れている可能性を示し、異常検知や原因分析の観点から重要な指標となります。
相関関係が崩れる理由
相関関係の崩れやノイズ増加が生じる原因として、以下のようなものが考えられます。
- 部品の摩耗や劣化:本来同期していた動作がずれ始める
- 制御系の不安定化:フィードバックが乱れ、信号間の位相が逆転する
- 外部ノイズの混入:センサ信号にランダム成分が加わり、相関が弱まる
- 環境変動:温度や振動など外部要因で信号が不規則になる
検出手法
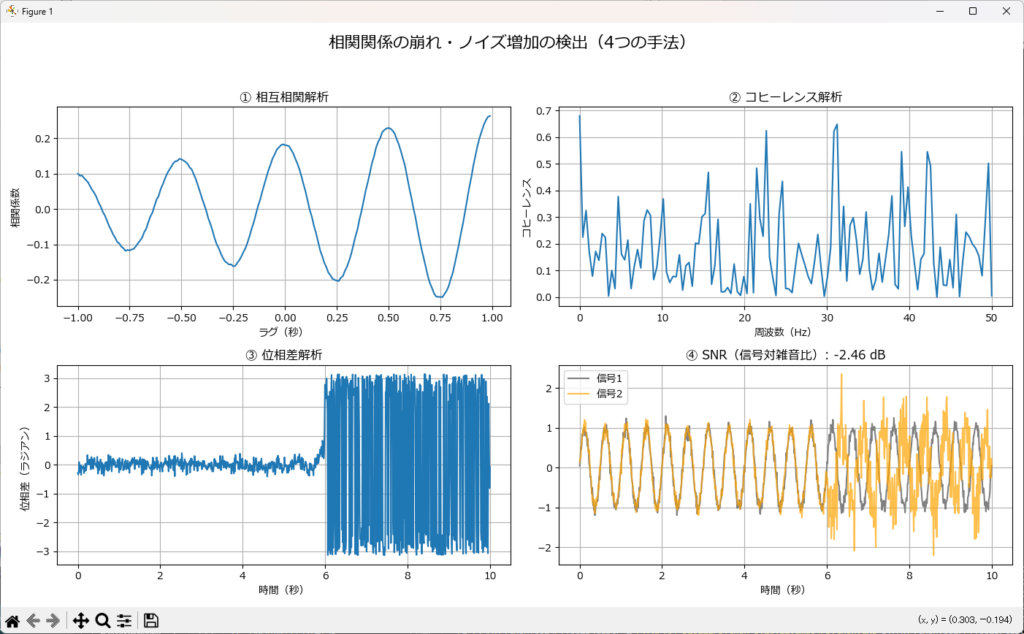
相関関係の崩れやノイズ増加を検出するためには、以下のような手法が有効です。
- 相互相関解析(Cross-Correlation):複数信号の相関係数を計算し、関係性の強弱を評価
- コヒーレンス解析(Coherence):周波数領域で信号間の関連性を評価
- 位相差解析:信号間の位相のずれを追跡し、逆転や乱れを検出
- ノイズ指標(SNR, Signal-to-Noise Ratio):信号に対するノイズの割合を定量化
よく使われる特徴量
相関関係の崩れやノイズ増加を定量的に捉えるために、以下のような特徴量がよく使われます。
- 相関係数(Correlation Coefficient)
信号間の線形関係を表す指標。値が1に近いほど強い相関、0に近いほど無相関。 - コヒーレンス値(Coherence Value)
周波数領域での信号間の関連性を表す。値が高いほど周波数成分が一致。 - 位相差(Phase Difference)
信号間の位相のずれを定量化。逆相関や同期崩れを検出できる。 - SNR(Signal-to-Noise Ratio)
信号に対するノイズの割合。値が低いほどノイズが多く、相関が崩れやすい。 - ノイズ分散(Noise Variance)
ノイズ成分のばらつきを表す。安定した信号では小さく、ノイズ増加時には大きくなる。
参考ソースコード
振幅の変化(検出方法)
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import find_peaks, hilbert
from scipy.ndimage import uniform_filter1d
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
# --- データ生成関数 ---
def generate_signal(seed=42):
"""
正弦波にノイズとスパイクを加えた信号を生成する。
Parameters:
seed (int): 乱数シード(再現性のため)
Returns:
x (ndarray): 時間軸(等間隔)
signal (ndarray): 生成された信号
"""
np.random.seed(seed)
x = np.linspace(0, 10, 500)
signal = np.sin(2 * np.pi * x) + 0.1 * np.random.randn(len(x))
signal[100] += 2.5
signal[300] -= 2.0
return x, signal
# --- 1. ピーク検出 ---
def detect_peaks(signal, height=1.5):
"""
ピーク(局所最大値)を検出する。
Parameters:
signal (ndarray): 入力信号
height (float): ピークとみなす最小高さ
Returns:
peaks (ndarray): ピークのインデックス配列
"""
peaks, _ = find_peaks(signal, height=height)
return peaks
# --- 2. 移動平均+しきい値 ---
def detect_moving_average_anomaly(signal, window=20, threshold=1.0):
"""
移動平均からの逸脱による異常検出。
Parameters:
signal (ndarray): 入力信号
window (int): 移動平均の窓幅
threshold (float): 平均からの逸脱しきい値
Returns:
moving_avg (ndarray): 移動平均系列
anomaly_idx (ndarray): 異常と判定されたインデックス
"""
moving_avg = uniform_filter1d(signal, size=window)
anomaly_idx = np.where(np.abs(signal - moving_avg) > threshold)[0]
return moving_avg, anomaly_idx
# --- 3. エンベロープ解析 ---
def detect_envelope_anomaly(signal, std_factor=2):
"""
エンベロープ(包絡線)を用いた振幅異常の検出。
Parameters:
signal (ndarray): 入力信号
std_factor (float): 標準偏差にかける倍率(しきい値)
Returns:
envelope (ndarray): 包絡線
anomaly_idx (ndarray): 異常と判定されたインデックス
threshold (float): 使用されたしきい値
"""
analytic_signal = hilbert(signal)
envelope = np.abs(analytic_signal)
threshold = np.mean(envelope) + std_factor * np.std(envelope)
anomaly_idx = np.where(envelope > threshold)[0]
return envelope, anomaly_idx, threshold
# --- 4. Zスコア ---
def detect_zscore_anomaly(signal, threshold=3):
"""
Zスコアによる外れ値検出。
Parameters:
signal (ndarray): 入力信号
threshold (float): Zスコアのしきい値(通常は2〜3)
Returns:
z_scores (ndarray): 各点のZスコア
anomaly_idx (ndarray): 異常と判定されたインデックス
threshold (float): 使用されたしきい値
"""
z_scores = (signal - np.mean(signal)) / np.std(signal)
anomaly_idx = np.where(np.abs(z_scores) > threshold)[0]
return z_scores, anomaly_idx, threshold
# --- 5. IQR ---
def detect_iqr_anomaly(signal):
"""
IQR(四分位範囲)による外れ値検出。
Parameters:
signal (ndarray): 入力信号
Returns:
lower (float): 下限しきい値
upper (float): 上限しきい値
anomaly_idx (ndarray): 異常と判定されたインデックス
"""
q1 = np.percentile(signal, 25)
q3 = np.percentile(signal, 75)
iqr = q3 - q1
lower = q1 - 1.5 * iqr
upper = q3 + 1.5 * iqr
anomaly_idx = np.where((signal < lower) | (signal > upper))[0]
return lower, upper, anomaly_idx
# --- 可視化 ---
def plot_all_methods(x, signal):
fig, axes = plt.subplots(1, 5, figsize=(20, 5), sharey=True)
# 1. ピーク検出
peaks = detect_peaks(signal)
axes[0].plot(x, signal, color='gray', label='信号')
axes[0].plot(x[peaks], signal[peaks], 'ro', label='ピーク')
axes[0].set_title("① ピーク検出")
axes[0].set_xlabel("時間")
axes[0].set_ylabel("振幅")
axes[0].legend()
axes[0].grid(True)
# 2. 移動平均+しきい値
moving_avg, ma_anomaly = detect_moving_average_anomaly(signal)
axes[1].plot(x, signal, color='gray', label='信号')
axes[1].plot(x, moving_avg, color='blue', linestyle='--', label='移動平均')
axes[1].plot(x[ma_anomaly], signal[ma_anomaly], 'bx', label='異常')
axes[1].set_title("② 移動平均+しきい値")
axes[1].set_xlabel("時間")
axes[1].legend()
axes[1].grid(True)
# 3. エンベロープ解析
envelope, env_anomaly, env_threshold = detect_envelope_anomaly(signal)
axes[2].plot(x, signal, color='gray', label='信号')
axes[2].plot(x, envelope, color='green', linestyle='--', label='エンベロープ')
axes[2].plot(x[env_anomaly], signal[env_anomaly], 'go', label='異常')
axes[2].set_title("③ エンベロープ解析")
axes[2].set_xlabel("時間")
axes[2].legend()
axes[2].grid(True)
# 4. Zスコア
z_scores, z_anomaly, z_threshold = detect_zscore_anomaly(signal)
axes[3].plot(x, signal, color='gray', label='信号')
axes[3].hlines([z_threshold, -z_threshold], x[0], x[-1], colors='red', linestyles='dotted', label='Zスコアしきい値')
axes[3].plot(x[z_anomaly], signal[z_anomaly], 'k*', label='異常')
axes[3].set_title("④ Zスコアによる外れ値検出")
axes[3].set_xlabel("時間")
axes[3].legend()
axes[3].grid(True)
# 5. IQR
lower, upper, iqr_anomaly = detect_iqr_anomaly(signal)
axes[4].plot(x, signal, color='gray', label='信号')
axes[4].hlines([lower, upper], x[0], x[-1], colors='orange', linestyles='dotted', label='IQRしきい値')
axes[4].plot(x[iqr_anomaly], signal[iqr_anomaly], 'ms', label='異常')
axes[4].set_title("⑤ IQRによる外れ値検出")
axes[4].set_xlabel("時間")
axes[4].legend()
axes[4].grid(True)
plt.suptitle("振幅変化の検出(5つの手法)", fontsize=16)
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.show()
if __name__ == "__main__":
# --- 実行 ---
x, signal = generate_signal()
plot_all_methods(x, signal)
周波数成分の変化(検出方法)
# pip install PyWavelets
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import stft, hilbert
from scipy.fft import fft, fftfreq
import pywt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
# --- 信号生成(周波数変化あり) ---
def generate_freq_shift_signal(seed=42):
"""
時間とともに周波数が変化する人工信号を生成する。
前半は5Hz、後半は20Hzの正弦波を結合し、ノイズを加えた非定常信号を作成する。
Parameters:
seed (int): 乱数シード(再現性のため)
Returns:
t (ndarray): 時間軸(秒)
signal (ndarray): 周波数変化を含む信号
"""
np.random.seed(seed)
t = np.linspace(0, 2, 1000)
signal = np.sin(2 * np.pi * 5 * t[:500]) # 前半:5Hz
signal = np.concatenate([signal, np.sin(2 * np.pi * 20 * t[500:])]) # 後半:20Hz
signal += 0.2 * np.random.randn(len(t)) # ノイズ追加
return t, signal
# --- 1. FFT ---
def compute_fft(signal, fs=500):
"""
フーリエ変換(FFT)で信号全体の周波数スペクトルを取得する。
時間情報は失われるが、信号に含まれる周波数成分の強度を一括で可視化できる。
Parameters:
signal (ndarray): 入力信号
fs (int): サンプリング周波数(Hz)
Returns:
freq (ndarray): 周波数軸(Hz)
spectrum (ndarray): 振幅スペクトル(絶対値)
"""
N = len(signal)
freq = fftfreq(N, d=1/fs)
spectrum = np.abs(fft(signal))
return freq[:N // 2], spectrum[:N // 2]
# --- 2. STFT ---
def compute_stft(signal, fs=500, nperseg=128):
"""
短時間フーリエ変換(STFT)で時間ごとの周波数変化を可視化する。
信号を短い時間窓に分割し、それぞれにFFTを適用することで、
周波数の時間的推移を捉える。
Parameters:
signal (ndarray): 入力信号
fs (int): サンプリング周波数(Hz)
nperseg (int): 各セグメントの長さ(サンプル数)
Returns:
f (ndarray): 周波数軸(Hz)
t (ndarray): 時間軸(秒)
Zxx (ndarray): 振幅スペクトログラム(|STFT|)
"""
f, t, Zxx = stft(signal, fs=fs, nperseg=nperseg)
return f, t, np.abs(Zxx)
# --- 3. ウェーブレット変換 ---
def compute_wavelet(signal, wavelet='morl', scales=np.arange(1, 128)):
"""
ウェーブレット変換(CWT)で多解像度の時間周波数解析を行う。
非定常信号や短時間の周波数変化を捉えるのに適しており、
スケールは周波数に相当する。
Parameters:
signal (ndarray): 入力信号
wavelet (str): 使用するウェーブレット(例: 'morl', 'cmor' など)
scales (array-like): スケール(周波数に対応)
Returns:
scales (ndarray): 使用したスケール
times (ndarray): 時間軸(サンプルインデックス)
coef (ndarray): ウェーブレット係数の絶対値(2次元配列)
"""
coef, freqs = pywt.cwt(signal, scales, wavelet)
return scales, np.arange(len(signal)), np.abs(coef)
# --- 4. スペクトルエンベロープ ---
def compute_spectral_envelope(signal):
"""
ヒルベルト変換を用いて信号のスペクトルエンベロープ(包絡線)を抽出する。
瞬時振幅を可視化することで、周波数成分の強度変化を滑らかに追跡できる。
Parameters:
signal (ndarray): 入力信号
Returns:
envelope (ndarray): 包絡線(瞬時振幅)
"""
analytic = hilbert(signal)
envelope = np.abs(analytic)
return envelope
# --- 可視化 ---
def plot_frequency_methods(t, signal, fs=500):
"""
周波数変化を検出する4つの手法を用いて信号を可視化する。
表示される手法:
① フーリエ変換(FFT)
② 短時間フーリエ変換(STFT)
③ ウェーブレット変換(CWT)
④ スペクトルエンベロープ解析(ヒルベルト変換)
Parameters:
t (ndarray): 時間軸(秒)
signal (ndarray): 入力信号
fs (int): サンプリング周波数(Hz)
"""
fig, axes = plt.subplots(2, 2, figsize=(14, 8))
# 1. FFT
freq, spectrum = compute_fft(signal, fs)
axes[0, 0].plot(freq, spectrum, color='blue')
axes[0, 0].set_title("① フーリエ変換(FFT)")
axes[0, 0].set_xlabel("周波数 [Hz]")
axes[0, 0].set_ylabel("振幅スペクトル")
axes[0, 0].grid(True)
# 2. STFT
f, tt, Z = compute_stft(signal, fs)
im1 = axes[0, 1].pcolormesh(tt, f, Z, shading='gouraud')
axes[0, 1].set_title("② 短時間フーリエ変換(STFT)")
axes[0, 1].set_xlabel("時間 [s]")
axes[0, 1].set_ylabel("周波数 [Hz]")
fig.colorbar(im1, ax=axes[0, 1])
# 3. ウェーブレット変換
scales, times, coef = compute_wavelet(signal)
im2 = axes[1, 0].imshow(coef, extent=[0, t[-1], scales[-1], scales[0]],
aspect='auto', cmap='viridis')
axes[1, 0].set_title("③ ウェーブレット変換")
axes[1, 0].set_xlabel("時間 [s]")
axes[1, 0].set_ylabel("スケール(周波数に相当)")
fig.colorbar(im2, ax=axes[1, 0])
# 4. スペクトルエンベロープ
envelope = compute_spectral_envelope(signal)
axes[1, 1].plot(t, signal, color='gray', label='信号')
axes[1, 1].plot(t, envelope, color='red', linestyle='--', label='エンベロープ')
axes[1, 1].set_title("④ スペクトルエンベロープ解析")
axes[1, 1].set_xlabel("時間 [s]")
axes[1, 1].set_ylabel("振幅")
axes[1, 1].legend()
axes[1, 1].grid(True)
plt.suptitle("周波数成分の変化検出(4つの手法)", fontsize=16)
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.show()
# --- 実行 ---
if __name__ == "__main__":
t, signal = generate_freq_shift_signal()
plot_frequency_methods(t, signal)
波形形状の変化(検出方法)
# pip install PyWavelets
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import correlate, find_peaks
from scipy.ndimage import uniform_filter1d
import pywt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
# --- 信号生成(形状変化あり) ---
def generate_shape_change_signal(seed=42):
"""
波形形状に変化を加えた信号を生成する。
前半は正弦波、途中に尖ったスパイクや歪みを挿入。
"""
np.random.seed(seed)
x = np.linspace(0, 10, 1000)
signal = np.sin(2 * np.pi * x)
signal[300:310] += 2.0 # スパイク
signal[600:650] *= 0.3 # 振幅の歪み
signal += 0.1 * np.random.randn(len(x)) # ノイズ
return x, signal
# --- 1. テンプレートマッチング ---
def detect_template_mismatch(signal, template):
"""
テンプレートマッチングにより波形の形状差異を検出する。
Parameters:
signal (ndarray): 入力信号
template (ndarray): 正常波形テンプレート
Returns:
similarity (ndarray): 相関係数の系列(類似度)
"""
corr = correlate(signal, template, mode='same')
norm_corr = corr / (np.linalg.norm(template) * np.linalg.norm(signal))
return norm_corr
# --- 2. 区間ごとの統計量比較 ---
def detect_statistical_change(signal, window=50):
"""
移動ウィンドウで平均と分散を計算し、形状の変化を検出する。
Parameters:
signal (ndarray): 入力信号
window (int): ウィンドウサイズ
Returns:
mean_series (ndarray): 移動平均
std_series (ndarray): 移動標準偏差
"""
mean_series = uniform_filter1d(signal, size=window)
std_series = uniform_filter1d((signal - mean_series)**2, size=window)**0.5
return mean_series, std_series
# --- 3. スパイク検出 ---
def detect_spikes(signal, threshold=2.0):
"""
スパイク(急激なピークや谷)を検出する。
Parameters:
signal (ndarray): 入力信号
threshold (float): ピークの高さのしきい値
Returns:
spike_idx (ndarray): スパイクのインデックス
"""
peaks, _ = find_peaks(signal, height=threshold)
troughs, _ = find_peaks(-signal, height=threshold)
return np.sort(np.concatenate([peaks, troughs]))
# --- 4. ウェーブレット解析 ---
def compute_wavelet_shape(signal, wavelet='db4', level=4):
"""
ウェーブレット分解により局所的な形状変化を検出する。
Parameters:
signal (ndarray): 入力信号
wavelet (str): ウェーブレットの種類(例: 'db4')
level (int): 分解レベル
Returns:
coeffs (list): 各スケールのウェーブレット係数
"""
coeffs = pywt.wavedec(signal, wavelet, level=level)
return coeffs
# --- 可視化 ---
def plot_shape_methods(x, signal):
"""
波形形状の変化を検出する4つの手法を可視化する。
"""
fig, axes = plt.subplots(2, 2, figsize=(14, 8))
# 1. テンプレートマッチング
template = np.sin(2 * np.pi * x[:100])
similarity = detect_template_mismatch(signal, template)
axes[0, 0].plot(x, similarity, color='purple')
axes[0, 0].set_title("① テンプレートマッチング")
axes[0, 0].set_xlabel("時間")
axes[0, 0].set_ylabel("類似度")
axes[0, 0].grid(True)
# 2. 区間ごとの統計量
mean_series, std_series = detect_statistical_change(signal)
axes[0, 1].plot(x, signal, color='gray', label='信号')
axes[0, 1].plot(x, mean_series, color='blue', label='移動平均')
axes[0, 1].plot(x, std_series, color='orange', label='移動標準偏差')
axes[0, 1].set_title("② 区間ごとの統計量比較")
axes[0, 1].set_xlabel("時間")
axes[0, 1].legend()
axes[0, 1].grid(True)
# 3. スパイク検出
spikes = detect_spikes(signal)
axes[1, 0].plot(x, signal, color='gray', label='信号')
axes[1, 0].plot(x[spikes], signal[spikes], 'ro', label='スパイク')
axes[1, 0].set_title("③ スパイク検出")
axes[1, 0].set_xlabel("時間")
axes[1, 0].legend()
axes[1, 0].grid(True)
# 4. ウェーブレット解析(詳細係数の可視化)
coeffs = compute_wavelet_shape(signal)
detail = coeffs[1] # 第1レベルの詳細成分
axes[1, 1].plot(detail, color='green')
axes[1, 1].set_title("④ ウェーブレット解析(詳細成分)")
axes[1, 1].set_xlabel("係数インデックス")
axes[1, 1].set_ylabel("振幅")
axes[1, 1].grid(True)
plt.suptitle("波形形状の変化検出(4つの手法)", fontsize=16)
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.show()
# --- 実行 ---
if __name__ == "__main__":
x, signal = generate_shape_change_signal()
plot_shape_methods(x, signal)
周期性の乱れ(検出方法)
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import find_peaks, correlate, stft
from scipy.fft import fft, fftfreq
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
# --- 信号生成(周期乱れあり) ---
def generate_irregular_period_signal(seed=42):
"""
周期が途中で乱れる信号を生成する。
前半は一定周期、後半は周期が徐々に変化。
"""
np.random.seed(seed)
t = np.linspace(0, 10, 1000)
signal = np.sin(2 * np.pi * 1 * t)
signal[500:] = np.sin(2 * np.pi * (1 + 0.5 * np.sin(2 * np.pi * 0.2 * t[500:])) * t[500:])
signal += 0.1 * np.random.randn(len(t))
return t, signal
# --- 1. 自己相関解析 ---
def compute_autocorrelation(signal):
"""
自己相関関数を計算し、周期性の乱れを検出する。
Returns:
lags (ndarray): ラグ(時間差)
acf (ndarray): 自己相関値
"""
n = len(signal)
signal = signal - np.mean(signal)
acf = correlate(signal, signal, mode='full') / np.var(signal) / n
lags = np.arange(-n + 1, n)
center = len(acf) // 2
return lags[center:], acf[center:]
# --- 2. ピーク間隔解析 ---
def compute_peak_intervals(signal, t, height=0.5):
"""
ピーク間隔を計測し、周期のばらつきを可視化する。
Returns:
peak_times (ndarray): ピークの時間位置
intervals (ndarray): ピーク間隔(秒)
"""
peaks, _ = find_peaks(signal, height=height)
peak_times = t[peaks]
intervals = np.diff(peak_times)
return peak_times[1:], intervals
# --- 3. FFT ---
def compute_fft(signal, fs=100):
"""
フーリエ変換で基本周波数の変動やピークの広がりを確認する。
Returns:
freq (ndarray): 周波数軸
spectrum (ndarray): 振幅スペクトル
"""
N = len(signal)
freq = fftfreq(N, d=1/fs)
spectrum = np.abs(fft(signal))
return freq[:N // 2], spectrum[:N // 2]
# --- 4. STFT ---
def compute_stft(signal, fs=100, nperseg=128):
"""
短時間フーリエ変換で時間ごとの周期変動を可視化する。
Returns:
f (ndarray): 周波数軸
t (ndarray): 時間軸
Zxx (ndarray): 振幅スペクトログラム
"""
f, t, Zxx = stft(signal, fs=fs, nperseg=nperseg)
return f, t, np.abs(Zxx)
# --- 可視化 ---
def plot_periodicity_methods(t, signal, fs=100):
fig, axes = plt.subplots(2, 2, figsize=(14, 8))
# 1. 自己相関
lags, acf = compute_autocorrelation(signal)
axes[0, 0].plot(lags / fs, acf)
axes[0, 0].set_title("① 自己相関解析")
axes[0, 0].set_xlabel("ラグ(秒)")
axes[0, 0].set_ylabel("相関")
axes[0, 0].grid(True)
# 2. ピーク間隔
peak_times, intervals = compute_peak_intervals(signal, t)
axes[0, 1].plot(peak_times, intervals, marker='o')
axes[0, 1].set_title("② ピーク間隔解析")
axes[0, 1].set_xlabel("時間(秒)")
axes[0, 1].set_ylabel("ピーク間隔(秒)")
axes[0, 1].grid(True)
# 3. FFT
freq, spectrum = compute_fft(signal, fs)
axes[1, 0].plot(freq, spectrum)
axes[1, 0].set_title("③ フーリエ変換(FFT)")
axes[1, 0].set_xlabel("周波数(Hz)")
axes[1, 0].set_ylabel("振幅")
axes[1, 0].grid(True)
# 4. STFT
f, tt, Z = compute_stft(signal, fs)
im = axes[1, 1].pcolormesh(tt, f, Z, shading='gouraud')
axes[1, 1].set_title("④ 時間周波数解析(STFT)")
axes[1, 1].set_xlabel("時間(秒)")
axes[1, 1].set_ylabel("周波数(Hz)")
fig.colorbar(im, ax=axes[1, 1])
plt.suptitle("周期性の乱れ検出(4つの手法)", fontsize=16)
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.show()
# --- 実行 ---
if __name__ == "__main__":
t, signal = generate_irregular_period_signal()
plot_periodicity_methods(t, signal)
相関関係の崩れ(検出方法)
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import correlate, coherence, hilbert
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
# --- 信号生成(相関崩れ+ノイズ) ---
def generate_correlated_signals(seed=42):
"""
相関していた2つの信号が途中から崩れたり、ノイズが増加する信号を生成する。
"""
np.random.seed(seed)
t = np.linspace(0, 10, 1000)
base = np.sin(2 * np.pi * 2 * t)
noise = 0.1 * np.random.randn(len(t))
signal1 = base + noise
signal2 = base + 0.1 * np.random.randn(len(t))
signal2[600:] = np.sin(2 * np.pi * 2 * t[600:] + np.pi) + 0.5 * np.random.randn(len(t[600:])) # 逆相+ノイズ増加
return t, signal1, signal2
# --- 1. 相互相関解析 ---
def compute_cross_correlation(sig1, sig2):
"""
相互相関を計算し、信号間の時間的な関係性を評価する。
"""
n = len(sig1)
sig1 = sig1 - np.mean(sig1)
sig2 = sig2 - np.mean(sig2)
corr = correlate(sig1, sig2, mode='full') / (np.std(sig1) * np.std(sig2) * n)
lags = np.arange(-n + 1, n)
center = len(corr) // 2
return lags[center - 100:center + 100], corr[center - 100:center + 100]
# --- 2. コヒーレンス解析 ---
def compute_coherence(sig1, sig2, fs=100):
"""
コヒーレンスを計算し、周波数ごとの信号間の関連性を評価する。
"""
f, Cxy = coherence(sig1, sig2, fs=fs, nperseg=256)
return f, Cxy
# --- 3. 位相差解析 ---
def compute_phase_difference(sig1, sig2):
"""
ヒルベルト変換を用いて信号間の瞬時位相差を計算する。
"""
h1 = hilbert(sig1)
h2 = hilbert(sig2)
phase1 = np.unwrap(np.angle(h1))
phase2 = np.unwrap(np.angle(h2))
phase_diff = np.mod(phase1 - phase2 + np.pi, 2 * np.pi) - np.pi
return phase_diff
# --- 4. SNR計算 ---
def compute_snr(signal, noise_estimate):
"""
信号対雑音比(SNR)を計算する。
Parameters:
signal (ndarray): 元の信号
noise_estimate (ndarray): ノイズ成分(例:信号との差分)
Returns:
snr_db (float): SNR(dB単位)
"""
power_signal = np.mean(signal ** 2)
power_noise = np.mean(noise_estimate ** 2)
snr = 10 * np.log10(power_signal / power_noise)
return snr
# --- 可視化 ---
def plot_correlation_noise_methods(t, sig1, sig2, fs=100):
fig, axes = plt.subplots(2, 2, figsize=(14, 8))
# 1. 相互相関
lags, corr = compute_cross_correlation(sig1, sig2)
axes[0, 0].plot(lags / fs, corr)
axes[0, 0].set_title("① 相互相関解析")
axes[0, 0].set_xlabel("ラグ(秒)")
axes[0, 0].set_ylabel("相関係数")
axes[0, 0].grid(True)
# 2. コヒーレンス
f, Cxy = compute_coherence(sig1, sig2, fs)
axes[0, 1].plot(f, Cxy)
axes[0, 1].set_title("② コヒーレンス解析")
axes[0, 1].set_xlabel("周波数(Hz)")
axes[0, 1].set_ylabel("コヒーレンス")
axes[0, 1].grid(True)
# 3. 位相差
phase_diff = compute_phase_difference(sig1, sig2)
axes[1, 0].plot(t, phase_diff)
axes[1, 0].set_title("③ 位相差解析")
axes[1, 0].set_xlabel("時間(秒)")
axes[1, 0].set_ylabel("位相差(ラジアン)")
axes[1, 0].grid(True)
# 4. SNR
noise = sig1 - sig2
snr_db = compute_snr(sig1, noise)
axes[1, 1].plot(t, sig1, label='信号1', color='gray')
axes[1, 1].plot(t, sig2, label='信号2', color='orange', alpha=0.7)
axes[1, 1].set_title(f"④ SNR(信号対雑音比): {snr_db:.2f} dB")
axes[1, 1].set_xlabel("時間(秒)")
axes[1, 1].legend()
axes[1, 1].grid(True)
plt.suptitle("相関関係の崩れ・ノイズ増加の検出(4つの手法)", fontsize=16)
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.show()
# --- 実行 ---
if __name__ == "__main__":
t, sig1, sig2 = generate_correlated_signals()
plot_correlation_noise_methods(t, sig1, sig2)
変化パターンごとのグラフ生成サンプル
このプログラムは、時系列信号に典型的な5種類の異常パターンを視覚的に表現するためのサンプルプログラムです。
正常な正弦波を基準に、異常区間(3〜6秒)でそれぞれ異なる変化を加えることで、異常検知でよく問題となる現象を表現しています。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo' # 日本語文字化け防止
# 時間軸
t = np.linspace(0, 10, 1000)
# 1. 振幅の変化(途中だけ振幅が大きくなる → その後戻る)
signal1 = np.sin(2 * np.pi * t)
signal1[(t > 3) & (t < 6)] *= 2
# 2. 周波数成分の変化(基本波に高周波成分が混ざる)
signal2 = np.sin(2 * np.pi * t)
signal2[(t > 3) & (t < 6)] += 0.5 * np.sin(8 * np.pi * t[(t > 3) & (t < 6)])
# 3. 波形形状の変化(途中だけ欠ける/潰れる)
signal3 = np.sin(2 * np.pi * t)
signal3[(t > 4) & (t < 5)] = 0 # 区間を欠けさせる
# 4. 周期性の乱れ(一部の周期が短くなる → 周波数2倍)
signal4 = np.sin(2 * np.pi * t)
# 区間3〜6秒を異常区間とする
mask = (t >= 3) & (t <= 6)
# 異常区間の時間軸をリセット(t=3をゼロに)
t_shifted = t[mask] - 3
# 周波数を2倍(周期1/2)にして速く振動させる
# 3秒時点で sin(2π*3)=0 → sin(0) で自然につながる
# 6秒時点で sin(4π*3)=sin(12π)=0 → ゼロクロスで復帰
signal4[mask] = np.sin(4 * np.pi * t_shifted)
# 6秒以降の時間軸もリセットして、元の波形に滑らかに復帰
t_after = t[t > 6] - 6
signal4[t > 6] = np.sin(2 * np.pi * t_after)
# 5. 相関関係の崩れ(位相が途中で逆転する2波形)
signal5a = np.sin(2 * np.pi * t) # 基準波形
signal5b = np.sin(2 * np.pi * t + np.pi/4) # 位相が少しずれた波形
# 区間3〜6で位相を逆転させる
signal5b[(t > 3) & (t < 6)] = np.sin(2 * np.pi * t[(t > 3) & (t < 6)] + np.pi)
# 描画
fig, axs = plt.subplots(5, 1, figsize=(10, 12))
axs[0].plot(t, signal1)
axs[0].set_title("振幅の変化(途中で増大)")
axs[0].grid(True)
axs[1].plot(t, signal2)
axs[1].set_title("周波数成分の変化(高周波混入)")
axs[1].grid(True)
axs[2].plot(t, signal3)
axs[2].set_title("波形形状の変化(欠ける例)")
axs[2].grid(True)
axs[3].plot(t, signal4)
axs[3].set_title("周期性の乱れ(周期が伸びる)")
axs[3].grid(True)
axs[4].plot(t, signal5a, label="信号A")
axs[4].plot(t, signal5b, label="信号B")
axs[4].set_title("相関関係の崩れ(位相逆転)")
axs[4].legend()
axs[4].grid(True)
plt.tight_layout()
plt.show()めとめ
本記事では、設備の異常検知の基本的な考え方から代表的な手法、そして振幅・周波数・波形形状・周期性・相関関係といった典型的な異常パターンについて解説しました。
異常検知は、単なる故障予知にとどまらず、生産性の向上・安全性の確保・コスト削減を同時に実現するための重要な技術です。データのクレンジングから特徴量設計、モデル適用、評価改善までを一貫した流れとして捉えることが、精度の高い検知につながります。
特にスライディングウィンドウによる局所的な特徴量抽出は、短時間の変化を捉える上で有効であり、現場での予兆保全に大きな力を発揮します。
今回紹介した考え方や手法が、皆さんのお役に立てば幸いです。








コメント