【Python実践】異常は波の“影”に現れる！側波帯で見抜く異常検知

2026年1月3日2026年1月4日

📡時系列データをフーリエ変換しても、スペクトルに異常は見つからない…。 そんなときは、波の奥にある“周波数の揺らぎ＝側波帯”に注目してみましょう。

本記事では、FM変調と側波帯の原理をやさしく解説しながら、 Pythonを使って信号を生成・可視化し、異常検知に応用する実践的な手法を紹介します。

側波帯とは

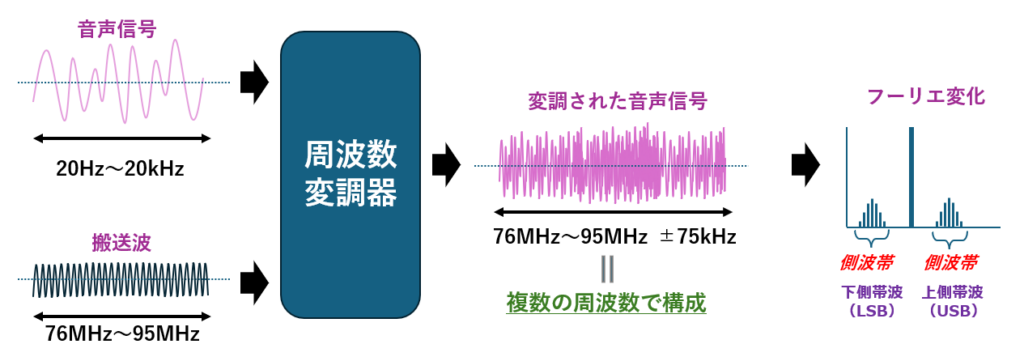
側波帯（そくはたい）」という言葉、聞き慣れないかもしれませんが、これは変調された信号の中に現れる“周波数の影”のような存在です。

たとえば、FM（周波数変調）では、音声などの情報を使って搬送波の周波数を揺らします。このとき、単一の周波数だった搬送波は、音声の周波数に応じて“揺れた形”になります。

この“揺れ”をフーリエ変換で周波数軸に変換すると、 搬送波の周囲に、音声の周波数成分がズラリと並んだ帯が現れます。これが側波帯（sidebands）です。

何故側波帯に着目するのか

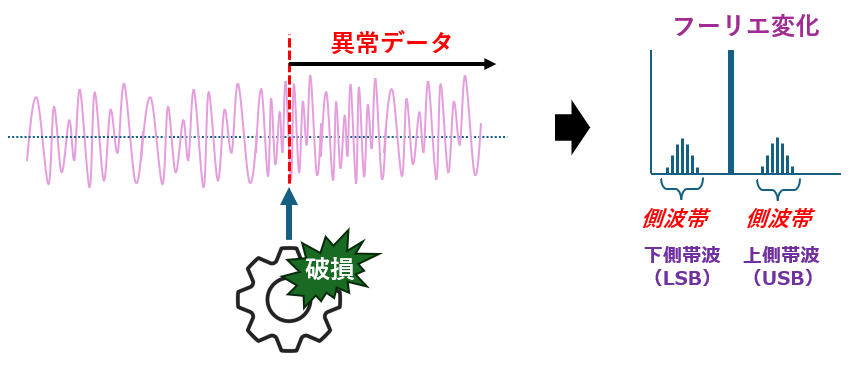
この側波帯は、元の信号の“変化”や“揺らぎ”を反映しているため、異常やノイズ、微細な変調の乱れが現れやすい場所でもあります。つまり、側波帯はただの“副産物”ではなく、 波の奥に隠れた情報を映し出す“影”のような存在です。

実は、FM変調のような通信信号でなくても、側波帯のような構造は現れます。たとえば、モーターの振動や機械の動作音など、周期的な信号に“異常”が加わると、 その揺らぎが周波数軸上で新たな成分として現れることがあります。

このとき、異常によって生じた周波数成分は、元の周期成分のまわりに現れるため、 まるで側波帯のようなパターンを形成します。

つまり、側波帯は“変調された信号”に限らず、 周期信号に異常が重なったときにも現れる特徴的なサインなのです。

だからこそ、異常検知の現場では、側波帯のような周波数の揺らぎに注目することで、 通常のスペクトル解析では見逃されがちな異常を見抜くことができるのです。

側波帯を異常検知に活用する

モーターやギアなどの回転機械は、通常、周期的な信号を発します。しかし、摩耗や破損といった異常が発生すると、その周期性が乱れ、信号に微細な揺らぎや変調が現れます。

下図は、故障発生時のデータ例です。

上段：センサーデータの時間波形。50秒の時点で異常発生。
左下：正常時の周波数スペクトル。　主成分のみが明瞭に現れ、他に目立った成分は無し。
右下：故障発生後のスペクトル。　中心周波数の周囲に複数の小さなピーク＝側波帯が出現。

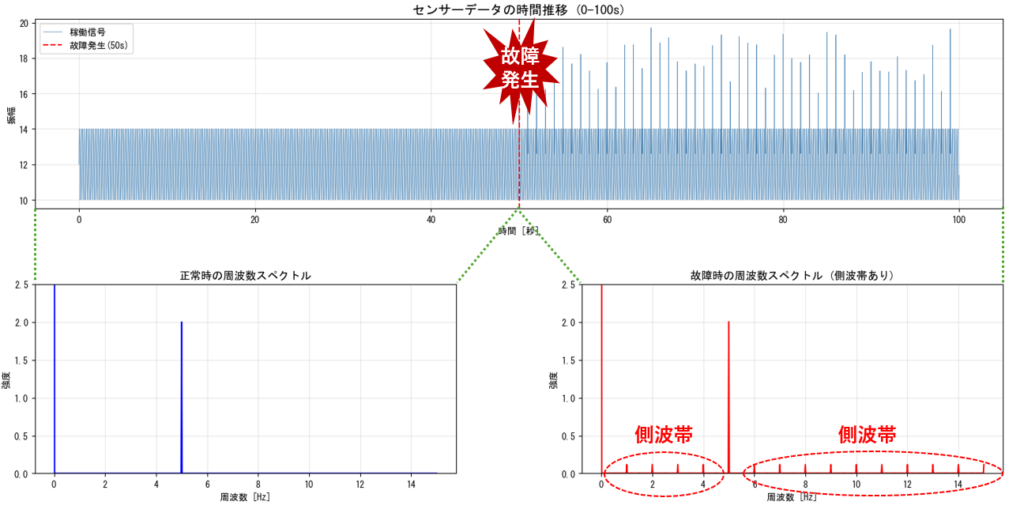
故障発生時の見られる側波帯は、以下のような異常によって生じることがあります。

軸の偏心やベアリングの損傷による振動の変調
ギアの欠けや摩耗による周期的な衝撃
外部からの干渉やノイズによる信号の揺らぎ

このように、時間軸では見逃されがちな異常も、周波数軸では側波帯として浮かび上がります。

つまり、側波帯は異常の“影”を映し出すレンズとして、通常のスペクトル解析に加えて、側波帯の出現や変化に注目することで、 より高精度な異常検知が可能になります。

側波帯の可視化と特徴量抽出

異常の“影”として現れる側波帯を活用するには、まずそれを周波数軸で可視化し、定量的に捉える必要があります。
下記はフーリエ変換と可視化のサンプルプログラムですが、コピペで使いやすくするため、関数化しています。

本章で紹介するプログラムを試される場合は、こちらからテストデータがダウンロード可能です。

フーリエ変換と側波帯エネルギー

側波帯エネルギーとは、中心周波数の周囲（±帯域）に含まれるスペクトル振幅の合計を指します。
たとえば、中心周波数が 6Hz、帯域幅が ±2Hz の場合、 4Hz〜8Hz の範囲にある振幅の合計値が energy になります。

あらかじめ正常な状態の energy を測定しておき、現在の energy がそれを大きく（通常は1.5倍以上）上回った場合、 異常の兆候があると判断します。

尚、異常の種類や進行度によって、影響を受ける周波数帯は異なることがあります。そのため、1つの帯域だけで判断するのではなく、複数の側波帯を同時に評価するのが一般的です。

6Hz ±2Hz の側波帯エネルギー: 64117.03
12Hz ±2Hz の側波帯エネルギー: 12605.47
18Hz ±2Hz の側波帯エネルギー: 8997.89

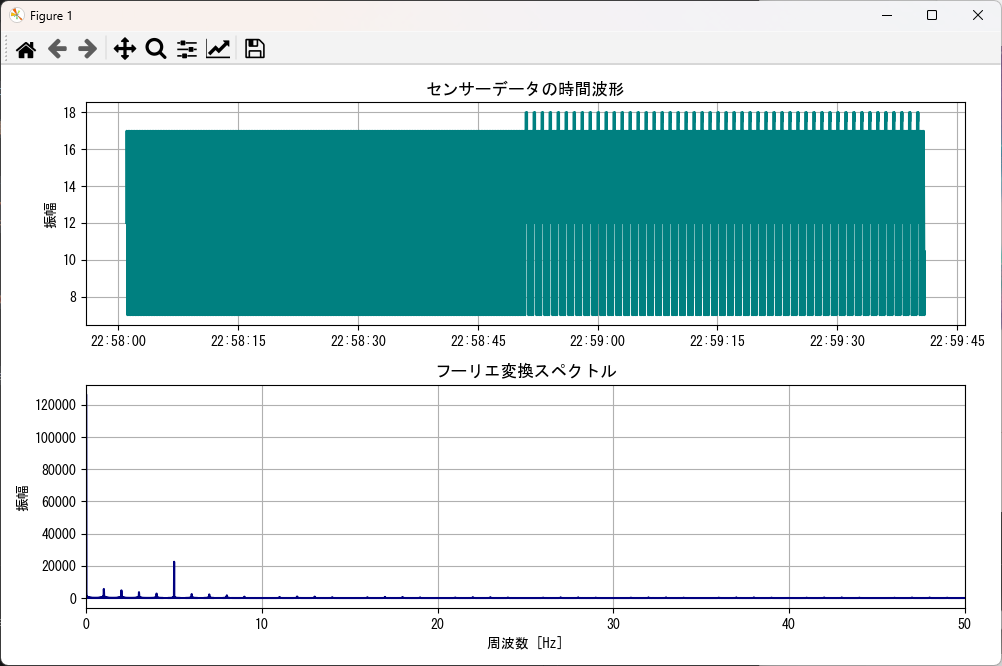
下記はフーリエ変換と測波帯エネルギーを出力するサンプルプログラムです。

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from scipy.fft import fft, fftfreq
plt.rcParams['font.family'] = 'MS Gothic'

# ------------------------------------------------------------
# 関数１：compute_fft関数（フーリエ変換＆複数側波帯エネルギー計算）
# ------------------------------------------------------------
def compute_fft(df, signal_column, time_column="timestamp", sidebands=None):
    """
    フーリエ変換と複数側波帯エネルギーの計算を行う

    Parameters:
        df            : センサーデータのDataFrame（時系列順）
        signal_column : 信号の列名（例: "vibration"）
        time_column   : タイムスタンプの列名
        sidebands     : [(中心周波数, 帯域幅), ...] のリスト

    Returns:
        xf            : 周波数軸（Hz）
        yf            : 振幅スペクトル
        energy_dict   : {中心周波数: 側波帯エネルギー} の辞書
    """
    y = df[signal_column].values
    t = df[time_column]
    dt = (t.iloc[1] - t.iloc[0]).total_seconds()

    n = len(y)
    yf = np.abs(fft(y))[:n // 2]
    xf = fftfreq(n, dt)[:n // 2]

    energy_dict = {}
    if sidebands:
        for center, width in sidebands:
            mask = (xf >= center - width) & (xf <= center + width)
            energy = np.sum(yf[mask])
            energy_dict[center] = energy

    return xf, yf, energy_dict

# --------------------------------------------------
# 時系列信号とそのフーリエ変換スペクトルのグラフ作成
# --------------------------------------------------
def plot_time_and_fft(df, signal_column, time_column="timestamp", fft_xlim=None):
    """
    時系列信号とそのフーリエ変換スペクトルを上下2段で可視化

    Parameters:
        df            : センサーデータのDataFrame（時系列順）
        signal_column : 信号の列名（例: "vibration"）
        time_column   : タイムスタンプの列名（デフォルト: "timestamp"）
        fft_xlim      : 下段スペクトルのx軸範囲（例: (0, 50)）

    Returns:
        なし（matplotlibでグラフを表示）
    """
    # 時系列データ
    t = df[time_column]
    y = df[signal_column]

    # サンプリング周期（秒）
    dt = (t.iloc[1] - t.iloc[0]).total_seconds()
    n = len(y)

    # フーリエ変換
    yf = np.abs(fft(y))[:n // 2]
    xf = fftfreq(n, dt)[:n // 2]

    # プロット
    fig, axes = plt.subplots(2, 1, figsize=(10, 6), sharex=False)

    # 上段：時間波形
    axes[0].plot(t, y, color="teal")
    axes[0].set_title("センサーデータの時間波形")
    axes[0].set_ylabel("振幅")
    axes[0].grid(True)

    # 下段：周波数スペクトル
    axes[1].plot(xf, yf, color="navy")
    axes[1].set_title("フーリエ変換スペクトル")
    axes[1].set_xlabel("周波数 [Hz]")
    axes[1].set_ylabel("振幅")
    if fft_xlim:
        axes[1].set_xlim(fft_xlim)
    axes[1].grid(True)

    plt.tight_layout()
    plt.show()


# ------------------------------------------------------------
# メインのサンプルプログラム
# ------------------------------------------------------------
if __name__ == "__main__":

    # 1. 読み込み
    df = pd.read_csv("simulated_vibration_anomaly_for_fft.csv", parse_dates=["timestamp"])
    df = df.sort_values("timestamp")

    # 2. FFTを実行する
    sidebands = [(6, 2), (12, 2), (18, 2)]
    xf, yf, energy_dict = compute_fft(df, signal_column="sensor_value", sidebands=sidebands)

    for center, energy in energy_dict.items():
        print(f"{center}Hz ±2Hz の側波帯エネルギー: {energy:.2f}")


    # 3. 可視化
    plot_time_and_fft(df, signal_column="sensor_value", fft_xlim=(0, 50))

側波帯エネルギーの変化プロット

ウィンドウ枠を設定し、それをスライドさせながら側波帯エネルギーの変化をプロットすることで、 異常の発生タイミングや進行の様子を時系列で可視化することができます。

この手法は、以下のような利点があります。

異常の兆候を早期に検出できる
異常の進行パターン（急激 or 徐々に）を把握できる
しきい値を超えるタイミングを明確に特定できる
異常検知アルゴリズムの設計や評価に活用できる

たとえば、以下のような折れ線グラフを描くことで、側波帯エネルギーがどの時点で急上昇し、どのように異常が進行したかを一目で把握できます。

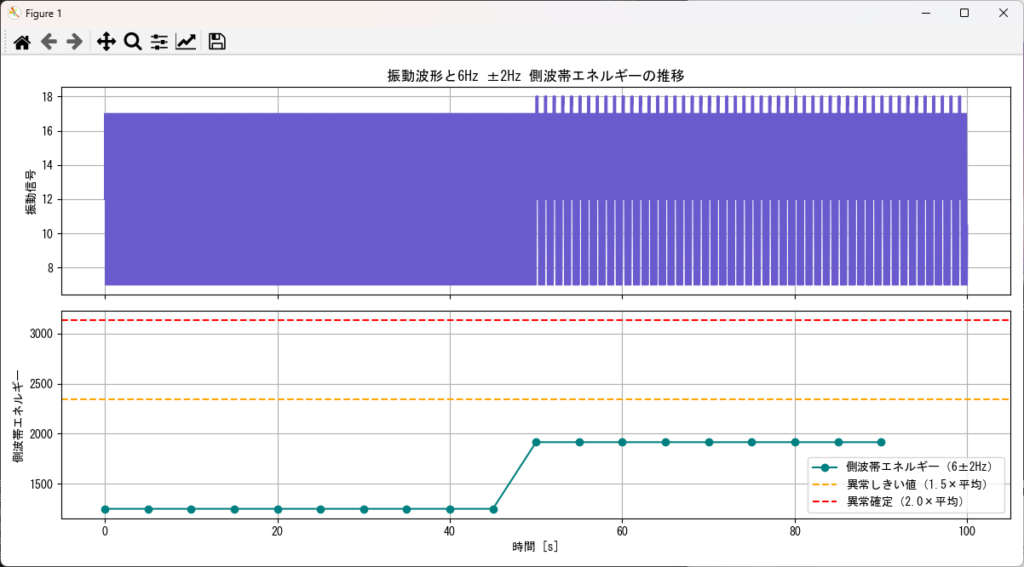
スライド量（ステップ幅）を1秒に設定すると、側波帯エネルギーの変化を滑らかに可視化できますが、その分計算回数が増加し、処理負荷が高くなります。一方で、スライド量を大きくすると計算は軽くなりますが、グラフが粗くなり、異常の兆候を見逃すリスクが高まります。
そのため、スライド量は通常、1秒〜ウィンドウサイズの範囲内で設定するのが一般的です。

ウインドウサイズはケースバーケースですが、おおよその目安を表にまとめておきます。

ウィンドウサイズ	特徴	向いてる用途
1〜2秒	高解像度、ノイズに敏感	瞬間的な異常の検出、リアルタイム監視
3〜5秒	バランス型	一般的な異常検知、周期性のある信号
10秒以上	平滑化される、変化に鈍感	長期傾向の把握、異常の進行パターン分析

下記のプログラムは、振動信号から側波帯エネルギーの時系列変化を解析し、異常の兆候や進行を可視化するためのサンプルです。

analyze_sideband_over_time 関数では、指定した周波数帯域に対してウィンドウをスライドさせながら側波帯エネルギーを計算し、あらかじめ設定した threshold に基づいて異常を判定します。結果は DataFrame として返されます。

plot_waveform_and_sideband 関数は、元の振動波形と側波帯エネルギーの推移を上下に並べて可視化します。時間軸の単位は "s"（秒）・"min"（分）・"auto"（自動判定）から選択可能です。

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from scipy.fft import fft, fftfreq
plt.rcParams['font.family'] = 'MS Gothic'

# ==========================================================================
#  ここに前述の関数１．（compute_fft関数）を丸ごと転記してください。
# ==========================================================================

# ------------------------------------------------------------------------------------------
# 関数２：analyze_sideband_over_time関数（時間的な側波帯エネルギーの変化と閾値による異常判定関数）
# ------------------------------------------------------------------------------------------
def analyze_sideband_over_time(
    df,
    signal_column,
    time_column="timestamp",
    sideband=(6, 2),
    window_sec=5,
    step_sec=5,
    threshold=20.0,
    verbose=True
):
    """
    一定間隔でウィンドウをスライドさせながら側波帯エネルギーを計算し、異常判定を行う

    Parameters:
        df            : センサーデータのDataFrame（時系列順）
        signal_column : 信号の列名（例: "vibration"）
        time_column   : タイムスタンプの列名（例: "timestamp"）
        sideband      : (中心周波数, 帯域幅) のタプル（例: (6, 2)）
        window_sec    : 解析ウィンドウの長さ（秒）
        step_sec      : スライド間隔（秒）
        threshold     : 異常判定のしきい値（側波帯エネルギー）
        verbose       : Trueならprint出力、Falseなら静かに返す

    Returns:
        result_df : 時間・エネルギー・判定を含むDataFrame
    """
    results = []
    timestamps = df[time_column]
    t_start = timestamps.min()
    t_end = timestamps.max()
    total_duration = (t_end - t_start).total_seconds()

    for offset in range(0, int(total_duration - window_sec) + 1, step_sec):
        t0 = t_start + pd.Timedelta(seconds=offset)
        t1 = t0 + pd.Timedelta(seconds=window_sec)
        df_window = df[(timestamps >= t0) & (timestamps < t1)]

        if len(df_window) < 2:
            continue  # スキップ（FFTできない）

        _, _, energy_dict = compute_fft(df_window, signal_column=signal_column, sidebands=[sideband])
        energy = energy_dict.get(sideband[0], 0.0)
        status = "正常" if energy < threshold else ("⚠ 異常兆候" if energy < threshold * 2 else "🚨 異常確定")

        if verbose:
            print(f"{offset:>3}s\t{energy:.1f}\t{status}")

        results.append({
            "時間": f"{offset}s",
            f"側波帯エネルギー（{sideband[0]}±{sideband[1]}Hz）": energy,
            "判定": status
        })

    return pd.DataFrame(results)

# ------------------------------------------------------------
# 側波帯エネルギーの変化を折れ線グラフで表示する関数
# ------------------------------------------------------------
def plot_waveform_and_sideband(
    df,
    result_df,
    signal_column,
    time_column,
    energy_column,
    title=None,
    time_unit="auto"  # "s", "min", or "auto"
):
    """
    元の波形と側波帯エネルギーの推移を上下に並べて可視化（時間単位を自動または指定）

    Parameters:
        ...
        time_unit : "s"（秒） / "min"（分） / "auto"（自動判定）
    """
    # 経過秒を計算
    t0 = df[time_column].iloc[0]
    df["elapsed_sec"] = (df[time_column] - t0).dt.total_seconds()
    total_duration_sec = df["elapsed_sec"].max()

    # 単位を決定
    if time_unit == "auto":
        time_unit = "min" if total_duration_sec >= 300 else "s"

    if time_unit == "min":
        df["elapsed"] = df["elapsed_sec"] / 60
        times = result_df["時間"].str.replace("s", "").astype(float) / 60
        xlabel = "時間 [分]"
    else:
        df["elapsed"] = df["elapsed_sec"]
        times = result_df["時間"].str.replace("s", "").astype(float)
        xlabel = "時間 [s]"

    # プロット
    fig, axs = plt.subplots(2, 1, figsize=(12, 6), sharex=True)
    axs[0].plot(df["elapsed"], df[signal_column], color="slateblue")
    axs[0].set_ylabel("振動信号")
    axs[0].set_title(title or "振動波形と側波帯エネルギーの推移")
    axs[0].grid(True)

    axs[1].plot(times, result_df[energy_column], marker="o", color="teal", label=energy_column)
    axs[1].axhline(y=result_df[energy_column].mean() * 1.5, color="orange", linestyle="--", label="異常しきい値（1.5×平均）")
    axs[1].axhline(y=result_df[energy_column].mean() * 2.0, color="red", linestyle="--", label="異常確定（2.0×平均）")
    axs[1].set_xlabel(xlabel)
    axs[1].set_ylabel("側波帯エネルギー")
    axs[1].grid(True)
    axs[1].legend()

    plt.tight_layout()
    plt.show()


# ------------------------------------------------------------
# メインのサンプルプログラム
# ------------------------------------------------------------
if __name__ == "__main__":

    import pandas as pd

    # 1. データ読み込
    df = pd.read_csv("simulated_vibration_anomaly_for_fft.csv", parse_dates=["timestamp"])
    df = df.sort_values("timestamp")

    # 2. 側波帯エネルギーをウィンドウごとに解析
    result_df = analyze_sideband_over_time(
        df,                                # センサーデータのDataFrame（時系列順）
        signal_column="sensor_value",     # 振動信号の列名
        sideband=(6, 2),                  # 中心周波数6Hz、±2Hzの帯域
        window_sec=5,                     # ウィンドウ幅（秒）
        step_sec=5,                       # スライドサイズ（秒）
        threshold=20.0,                   # 異常判定のしきい値（エネルギー）
        verbose=True                      # Trueでログ出力を有効化
    )

    # 3. 折れ線グラフで可視化
    plot_waveform_and_sideband(
        df,
        result_df,
        signal_column="sensor_value",
        time_column="timestamp",
        energy_column="側波帯エネルギー（6±2Hz）",
        title="振動波形と6Hz ±2Hz 側波帯エネルギーの推移",
        time_unit="auto"
    )

0s 1250.0 🚨 異常確定
5s 1250.0 🚨 異常確定
10s 1250.0 🚨 異常確定
～～～中略～～～～
85s 1915.8 🚨 異常確定
90s 1915.8 🚨 異常確定

機械学習との組み合わせ

側波帯エネルギーは、機械学習モデルの入力特徴量として利用できます。単一の周波数帯だけでなく、複数の帯域（例：6±2Hz, 12±2Hz など）を同時に解析することで、多次元の特徴ベクトルを構築できます。

本章で紹介するプログラムを試される場合は、こちらからテストデータがダウンロード可能です。

Isolation Forest による教師なし異常検知＋可視化

異常ラベルが存在しない場合は、Isolation Forest や One-Class SVM などの教師なし機械学習を用いることで、正常なパターンからの逸脱を自動的に検出できます。

以下のコードでは、次の処理を行っています。

側波帯エネルギーの計算：
analyze_sideband_over_time 関数で、指定した周波数帯（例：6±2Hz）の側波帯エネルギーをウィンドウごとに算出します。
統計特徴量の抽出：
各ウィンドウに対して、平均・標準偏差・最大値・最小値などの統計的特徴量を計算し、側波帯エネルギーと組み合わせて、異常検知に必要な多次元の特徴量セットを構築します。
異常スコアの付与：
detect_anomalies_unsupervised 関数で Isolation Forest を適用し、複数の特徴量をもとに各ウィンドウの異常スコア（1: 正常, -1: 異常）を自動的に判定します。
異常の可視化：
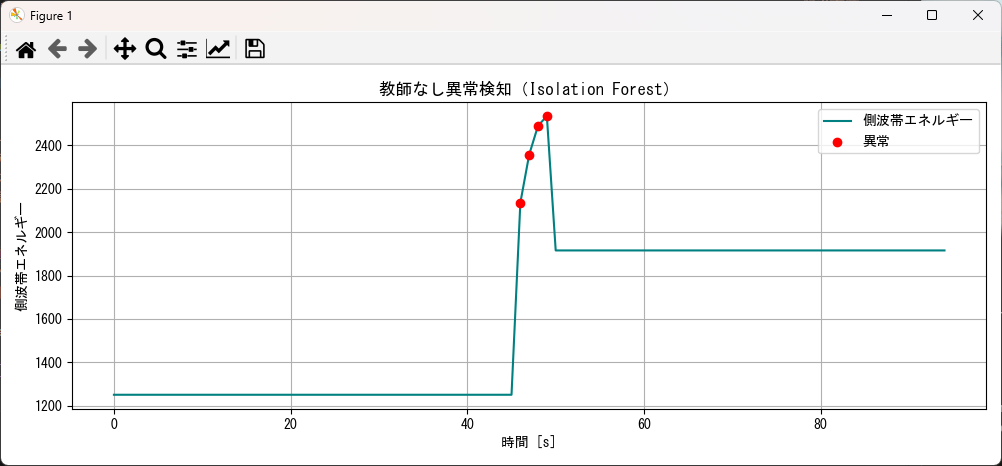
plot_anomaly_detection 関数で、側波帯エネルギーの時間推移とともに、異常と判定されたウィンドウを赤い点で可視化します。

このアプローチにより、しきい値を手動で設定することなく、異常の兆候を自動的に検出・可視化することができます。設備の状態監視や予兆保全の初期ステップとして、非常に有効な手法です。

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from scipy.fft import fft, fftfreq
plt.rcParams['font.family'] = 'MS Gothic'

# ===============================================================================
#  ここに前述の関数１．（compute_fft関数）を丸ごと転記してください。
# ===============================================================================

# ===============================================================================
#  ここに前述の関数２．（analyze_sideband_over_time関数）を丸ごと転記してください。
# ===============================================================================



from sklearn.ensemble import IsolationForest

# --------------------------------------------------
# solation Forestによる異常検知（教師なし）
# --------------------------------------------------
def detect_anomalies_unsupervised(result_df, feature_columns, contamination=0.1, random_state=42):
    """
    Isolation Forest による教師なし異常検知（多変量対応）

    Parameters:
        result_df       : 特徴量を含むDataFrame
        feature_columns : 使用する特徴量の列名リスト
        contamination   : 異常の割合（全体に対する異常の想定比率）
        random_state    : 乱数シード（再現性のため）

    Returns:
        result_df       : 異常スコア列を追加したDataFrame（-1: 異常, 1: 正常）
        model           : 学習済みのIsolationForestモデル
    """
    X = result_df[feature_columns]

    model = IsolationForest(contamination=contamination, random_state=random_state)
    result_df["異常スコア"] = model.fit_predict(X)

    return result_df, model

# -------------------------------
# 異常スコアの可視化
# -------------------------------
def plot_anomaly_detection(result_df, energy_column):
    times = result_df["時間"].str.replace("s", "").astype(float)
    energies = result_df[energy_column]
    scores = result_df["異常スコア"]

    plt.figure(figsize=(10, 4))
    plt.plot(times, energies, label="側波帯エネルギー", color="teal")
    plt.scatter(times[scores == -1], energies[scores == -1], color="red", label="異常", zorder=5)
    plt.xlabel("時間 [s]")
    plt.ylabel("側波帯エネルギー")
    plt.title("教師なし異常検知（Isolation Forest）")
    plt.grid(True)
    plt.legend()
    plt.tight_layout()
    plt.show()

# -------------------------------------------------------
# ウィンドウ幅を指定して特徴量を計算＆カラム追加
# -------------------------------------------------------
def compute_stat_features(df, signal_column, time_column, window_sec, step_sec):
    """
    ウィンドウごとに統計特徴量を計算して返す
    """
    results = []
    timestamps = df[time_column]
    t_start = timestamps.min()
    t_end = timestamps.max()
    total_duration = (t_end - t_start).total_seconds()

    for offset in range(0, int(total_duration - window_sec) + 1, step_sec):
        t0 = t_start + pd.Timedelta(seconds=offset)
        t1 = t0 + pd.Timedelta(seconds=window_sec)
        df_window = df[(timestamps >= t0) & (timestamps < t1)]

        if len(df_window) < 2:
            continue

        y = df_window[signal_column].values
        results.append({
            "時間": f"{offset}s",
            "平均": np.mean(y),
            "標準偏差": np.std(y),
            "最大値": np.max(y),
            "最小値": np.min(y)
        })

    return pd.DataFrame(results)



# -------------------------------
# メイン処理
# -------------------------------
if __name__ == "__main__":

    # データ読み込み
    df = pd.read_csv("simulated_vibration_anomaly_for_fft.csv", parse_dates=["timestamp"])
    df = df.sort_values("timestamp")

    # 側波帯エネルギーを解析
    result_df = analyze_sideband_over_time(
        df,
        signal_column="sensor_value",
        time_column="timestamp",
        sideband=(6, 2),
        window_sec=5,
        step_sec=1,
        threshold=20.0,
        verbose=False
    )

    # 元の特徴量（側波帯エネルギー）から統計情報により他の特徴量を作成
    stat_df = compute_stat_features(df, "sensor_value", "timestamp", window_sec=5, step_sec=1)
    
    # 元の特徴量（側波帯エネルギー）と統計計算による他の特徴量をマージ
    result_df = pd.merge(result_df, stat_df, on="時間")

    # 全ての特徴量リスト
    feature_cols = [
        "側波帯エネルギー（6±2Hz）",
        "平均", "標準偏差", "最大値", "最小値"
    ]

    # 教師なし異常検知（多変量）
    result_df, model = detect_anomalies_unsupervised(result_df, feature_cols)

    # 結果表示
    print(result_df[["時間"] + feature_cols + ["異常スコア"]])
    print("\n異常スコアの内訳:")
    print(result_df["異常スコア"].value_counts())

    # グラフ表示（側波帯エネルギーを軸に可視化）
    plot_anomaly_detection(result_df, "側波帯エネルギー（6±2Hz）")

異常スコアの内訳:
異常スコア
1 91
-1 4

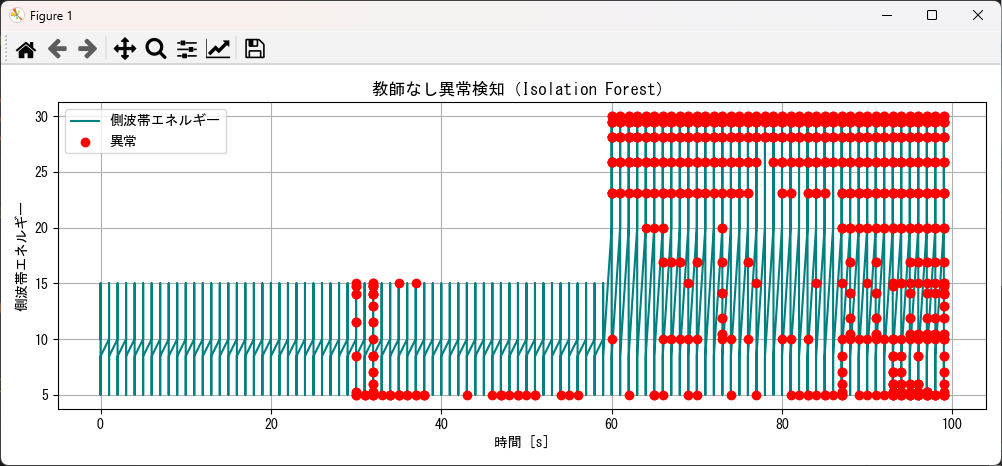
複数信号の関係性を活かした教師なし異常検知

異常は、単一の信号の変化だけでなく、複数の信号間の関係性の乱れとして現れることがあります。

スパイクが出ているのにノイズが少ない → 不自然な組み合わせ
トレンドが急上昇しているのにベース信号が停滞している → 故障の兆候かも？
周波数成分に異常があるのに、時系列の変化が小さい → 潜在的な異常の可能性

こうした複雑なパターンを捉えるには、複数の信号を同時に扱い、正解ラベルをもとに学習する教師ありの多変量モデルが有効です。

前述の「Isolation Forest による教師なし異常検知＋可視化」に記載したサンプルプログラムの __main__ を書きに書き換えて実行してください。

# -------------------------------
# メイン処理
# -------------------------------
if __name__ == "__main__":
    import pandas as pd

    # データ読み込み
    df = pd.read_csv("multivariate_simulation.csv", parse_dates=["timestamp"])
    df = df.sort_values("timestamp")

    # 特徴量の列名（すべての信号を使う）
    feature_cols = [
        "base_signal",
        "noise_component",
        "spike_component",
        "trend_component",
        "modulated_signal"
    ]

    # 教師なし異常検知（多変量）
    result_df, model = detect_anomalies_unsupervised(df.copy(), feature_cols)

    # 結果表示
    print(result_df[["timestamp"] + feature_cols + ["異常スコア"]])
    print("\n異常スコアの内訳:")
    print(result_df["異常スコア"].value_counts())

    # 可視化（例：modulated_signal を軸に）
    result_df["時間"] = (result_df["timestamp"] - result_df["timestamp"].iloc[0]).dt.total_seconds().astype(int).astype(str) + "s"
    plot_anomaly_detection(result_df, "modulated_signal")

複数信号の関係性を活かした教師あり異常検知

ラベル付きデータがある場合、教師あり学習を用いることで、異常のパターンを明示的に学習し、高精度な異常検知が可能になります。特に、複数の信号を組み合わせた多変量特徴量を使うことで、より複雑な異常の兆候を捉えることができます。

処理の流れ

1. ラベルの付与：
事前に定義したルール（例：spike_component > 6.0 または modulated_signal > 15.0）に基づいて、各データに異常ラベル（0＝正常、1＝異常）を付与します。
2. 特徴量の構築：
複数の信号成分に加え、周波数領域から抽出した側波帯エネルギー（6±2Hz）を特徴量として使用します。
3. ウィンドウ処理：
時系列データを一定時間幅（例：5秒）で区切り、各ウィンドウ内の信号の平均値を計算。これにより、局所的な変動を平滑化し、安定した特徴量を得ます。
4. 教師あり分類：
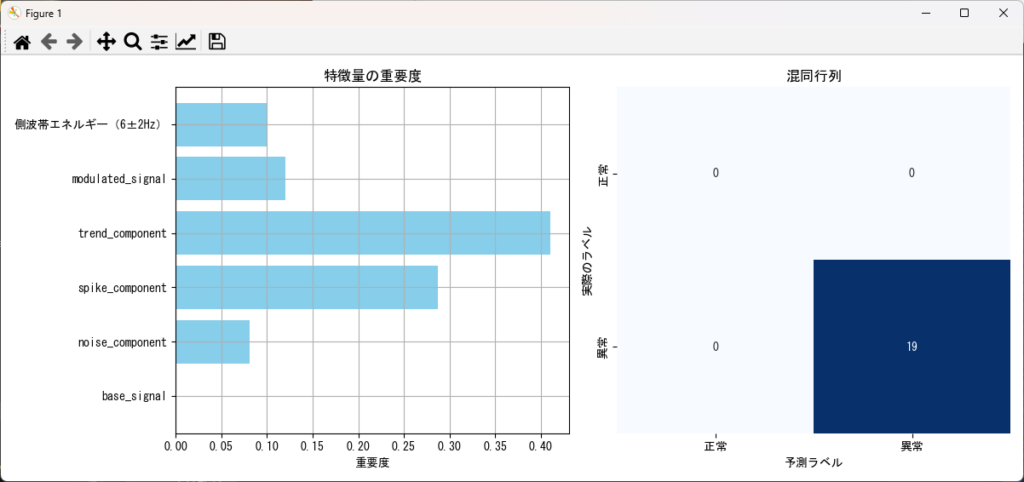
RandomForestClassifier を用いて、ウィンドウごとの特徴量とラベルを学習。未知データに対して異常かどうかを予測します。
5. 成績と可視化：
分類結果を混同行列で可視化し、モデルの精度を評価。さらに、特徴量の重要度グラフを表示することで、どの信号が異常検知に寄与しているかを分析します。

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from scipy.fft import fft, fftfreq
plt.rcParams['font.family'] = 'MS Gothic'

# ===============================================================================
#  ここに前述の関数１．（compute_fft関数）を丸ごと転記してください。
# ===============================================================================

# ===============================================================================
#  ここに前述の関数２．（analyze_sideband_over_time関数）を丸ごと転記してください。
# ===============================================================================



# --------------------------------------------------
# Random Forestによる教師あり学習
# --------------------------------------------------

from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix

# --- 関数：教師あり分類（時系列対応） ---
def train_and_evaluate_timeseries_classifier(
    df,
    target_column,
    feature_columns,
    test_ratio=0.2,
    random_state=42,
    verbose=True
):
    n_total = len(df)
    n_test = int(n_total * test_ratio)
    n_train = n_total - n_test

    df_train = df.iloc[:n_train]
    df_test = df.iloc[n_train:]

    X_train = df_train[feature_columns]
    y_train = df_train[target_column]
    X_test = df_test[feature_columns]
    y_test = df_test[target_column]

    clf = RandomForestClassifier(n_estimators=100, random_state=random_state)
    clf.fit(X_train, y_train)

    y_pred = clf.predict(X_test)

    if verbose:
        print("\n=== 教師あり分類（Random Forest） ===")
        print("=== 混同行列 ===")
        print(confusion_matrix(y_test, y_pred))
        print("\n=== 分類レポート ===")
        print(classification_report(y_test, y_pred))

    return clf, X_test, y_test, y_pred


# --------------------------------------------------
# 時系列信号に対してウィンドウ平均を計算する
# --------------------------------------------------
def compute_signal_window_means(df, signal_columns, time_column, window_sec, step_sec):
    """
    時系列信号に対してウィンドウ平均を計算し、各ウィンドウごとの特徴量を生成する。

    Parameters:
        df (pd.DataFrame): 時系列データを含むDataFrame（timestamp列と信号列を含む）
        signal_columns (list of str): 平均を計算する対象の信号列名リスト
        time_column (str): 時間情報を持つ列名（datetime型であること）
        window_sec (int): ウィンドウサイズ（秒単位）
        step_sec (int): ウィンドウのステップ幅（秒単位）

    Returns:
        pd.DataFrame: 各ウィンドウごとに平均を計算した特徴量を含むDataFrame。
                      "時間"列にはウィンドウの開始時刻（秒単位）が文字列で格納される。

    Notes:
        - 各ウィンドウ内に2点以上のデータが存在する場合のみ計算対象とする。
        - 特徴量はウィンドウ内の単純平均。
        - ウィンドウは非重複でも重複でも可（step_sec < window_sec で重複）。

    Reference:
        Fulcher, B. D., & Jones, N. S. (2014). 
        "Highly comparative feature-based time-series classification." 
        IEEE Transactions on Knowledge and Data Engineering.
    """
    results = []
    timestamps = df[time_column]
    t_start = timestamps.min()
    t_end = timestamps.max()
    total_duration = (t_end - t_start).total_seconds()

    for offset in range(0, int(total_duration - window_sec) + 1, step_sec):
        t0 = t_start + pd.Timedelta(seconds=offset)
        t1 = t0 + pd.Timedelta(seconds=window_sec)
        df_window = df[(timestamps >= t0) & (timestamps < t1)]

        if len(df_window) < 2:
            continue

        row = {"時間": f"{offset}s"}
        for col in signal_columns:
            row[col] = df_window[col].mean()
        results.append(row)

    return pd.DataFrame(results)



# ---------------------------------------------------------------
# 時系列データに対して、ウィンドウごとに異常ラベルを集約する
# ---------------------------------------------------------------
def compute_window_labels(df, time_column, label_column, window_sec, step_sec):
    """
    時系列データに対して、ウィンドウごとに異常ラベルを集約する関数。
    ウィンドウ内に1つでも異常（label=1）があれば、そのウィンドウ全体を異常とみなす。

    Parameters:
        df (pd.DataFrame): ラベル付きの時系列データ
        time_column (str): 時間列の名前（datetime型）
        label_column (str): ラベル列の名前（0 or 1）
        window_sec (int): ウィンドウサイズ（秒）
        step_sec (int): ステップ幅（秒）

    Returns:
        pd.DataFrame: 各ウィンドウごとのラベル（"時間", "label"列を含む）
    """
    results = []
    timestamps = df[time_column]
    t_start = timestamps.min()
    t_end = timestamps.max()
    total_duration = (t_end - t_start).total_seconds()

    for offset in range(0, int(total_duration - window_sec) + 1, step_sec):
        t0 = t_start + pd.Timedelta(seconds=offset)
        t1 = t0 + pd.Timedelta(seconds=window_sec)
        df_window = df[(timestamps >= t0) & (timestamps < t1)]

        if len(df_window) < 2:
            continue

        # ウィンドウ内に1つでも異常があれば 1、なければ 0
        label = int(df_window[label_column].max())
        results.append({"時間": f"{offset}s", "label": label})

    return pd.DataFrame(results)


# ---------------------------------------------------------------
# 同行列をヒートマップで描画
# ---------------------------------------------------------------
import seaborn as sns
from sklearn.metrics import confusion_matrix

def plot_confusion_matrix(y_true, y_pred, labels=[0, 1], ax=None):
    """
    混同行列をヒートマップで可視化する関数

    Parameters:
        y_true (array-like): 正解ラベル
        y_pred (array-like): 予測ラベル
        labels (list): ラベルの順序（デフォルトは [0, 1]）
        ax (matplotlib.axes): 描画先のAxes（省略可）
    """
    cm = confusion_matrix(y_true, y_pred, labels=labels)
    sns.heatmap(cm, annot=True, fmt="d", cmap="Blues", cbar=False,
                xticklabels=["正常", "異常"], yticklabels=["正常", "異常"],
                ax=ax)
    if ax:
        ax.set_xlabel("予測ラベル")
        ax.set_ylabel("実際のラベル")
        ax.set_title("混同行列")


# ---------------------------------------------------------------
# 同行列ヒートマップと特徴量を１枚に描画
# ---------------------------------------------------------------
def plot_feature_importance_and_confusion_matrix(clf, feature_names, y_true, y_pred):
    """
    特徴量の重要度と混同行列を1つの図にまとめて表示する関数

    Parameters:
        clf: 学習済みの分類器（feature_importances_ 属性を持つもの）
        feature_names: 特徴量名のリスト
        y_true: 正解ラベル
        y_pred: 予測ラベル
    """
    fig, axes = plt.subplots(1, 2, figsize=(12, 5))

    # 特徴量の重要度
    importances = clf.feature_importances_
    axes[0].barh(feature_names, importances, color="skyblue")
    axes[0].set_title("特徴量の重要度")
    axes[0].set_xlabel("重要度")
    axes[0].grid(True)

    # 混同行列
    plot_confusion_matrix(y_true, y_pred, ax=axes[1])

    plt.tight_layout()
    plt.show()


# -------------------------------
# メイン処理
# -------------------------------
if __name__ == "__main__":
    """
    教師あり異常検知パイプライン（Random Forest）
    ...
    """

    # データ読み込み
    df = pd.read_csv("multivariate_simulation_for_fft.csv", parse_dates=["timestamp"])
    df = df.sort_values("timestamp")

    # 信号列を定義（← ここがポイント！）
    signal_cols = [
        "base_signal",
        "noise_component",
        "spike_component",
        "trend_component",
        "modulated_signal"
    ]

    # ラベル付け
    df["label"] = ((df["spike_component"] > 6.0) | (df["modulated_signal"] > 15.0)).astype(int)

    # 側波帯エネルギーを計算
    result_df = analyze_sideband_over_time(
        df,
        signal_column="modulated_signal",
        time_column="timestamp",
        sideband=(6, 2),
        window_sec=5,
        step_sec=1,
        threshold=20.0,
        verbose=False
    )

    # 信号のウィンドウ平均を計算
    signal_df = compute_signal_window_means(df, signal_cols, "timestamp", window_sec=5, step_sec=1)

    # ラベルをウィンドウ単位に変換
    label_df = compute_window_labels(df, "timestamp", "label", window_sec=5, step_sec=1)

    # 特徴量とラベルをマージ
    result_df = pd.merge(result_df, signal_df, on="時間")
    result_df = pd.merge(result_df, label_df, on="時間")

    # 特徴量リスト（信号＋側波帯エネルギー）
    feature_cols = signal_cols + ["側波帯エネルギー（6±2Hz）"]

    # 教師あり分類（Random Forest）
    clf, X_test, y_test, y_pred = train_and_evaluate_timeseries_classifier(
        result_df,
        target_column="label",
        feature_columns=feature_cols,
        test_ratio=0.2
    )

    # 分類結果と特徴量の重要度をまとめて可視化！
    plot_feature_importance_and_confusion_matrix(
        clf=clf,
        feature_names=feature_cols,
        y_true=y_test,
        y_pred=y_pred
    )

=== 分類レポート ===
precision recall f1-score support
1 1.00 1.00 1.00 19

accuracy 1.00 19

macro avg 1.00 1.00 1.00 19
weighted avg 1.00 1.00 1.00 19