異常検知や予兆保全のアルゴリズムを作りたいけれど、「本物の異常データ」が手元にない──そんな悩み、ありませんか?
単なる乱数ではリアルさに欠けるし、実データはなかなか手に入らない。 そこで、サイン波・トレンド・突発ノイズなどを自由に組み合わせて、直感的に「それっぽい信号」を合成できるクラスを作りました。
このクラスは、もともと本記事で紹介するサンプルプログラム用に作ったものですが、思いのほか汎用性が高く、異常検知のテストやセンサーデータの模擬生成にも使えるので、ぜひ紹介したいと思います!
SignalComposerとは
SignalComposer は、一言で言えば、 「複数の時間系列信号を、パズルのように組み合わせて、リアリティのある疑似データを作るためのビルダー」です。
データ分析やAI開発の現場では、綺麗なサイン波や単純な正規分布ノイズを生成するのは簡単です。 でも、実際のセンサーデータはもっと“汚く”、そして“文脈”を持っているもの。
たとえば、ゆるやかなトレンドの上に周期的な振動が重なり、そこに突発的なスパイクやノイズが混じる── そんな複雑で現実的な信号を、直感的に合成できるツールが欲しい! そんな思いから、この SignalComposer を開発しました。
SignalComposer の設計思想
SignalComposer の根底にあるのは、「現実に近い信号を、プログラム上で柔軟かつ直感的に組み立てること」という思想です。単に数式を羅列するのではなく、エンジニアが現場で遭遇する「生きたデータ」を再現するために、以下の5つの柱で設計されています。
1. 🧩 生成 (Generate) と加工 (Process) の分離
信号作成のプロセスを「波形を生み出す工程」と「波形を変化させる工程」に明確に分離しました。
- Generate:
generate_signal(Sin/Cos/矩形波)、generate_noise(ノイズ)、generate_spike(突発異常) などでベースを作ります。 - Process: 作成した波形に対し、
limit(飽和)、decay(減衰)、multiply(増幅)、trend(ドリフト) などの物理的特性を後から付与します。 これらをパイプラインのように組み合わせることで、複雑なシナリオも整理されたコードで記述できます。
2. 🕰️ 時間軸と単位の柔軟性
時系列データの扱いで最も手間がかかる「サンプリング周期の管理」と「単位変換」を自動化しています。
- 共通のタイムライン: すべての信号はインスタンス生成時に設定した
start_timeとsampling_periodを基準に生成されるため、異なる信号同士でもインデックス(DatetimeIndex)が完全に一致します。 - 直感的な単位指定: 引数には数値だけでなく、
"100ms","10Hz","10m"(10分) といった文字列が使用可能です。「100ミリ秒周期で、10ヘルツの波形を作る」といった思考をそのままコードに落とし込めます。
3. 🎛️ 「揺らぎ」と「物理挙動」の再現
綺麗な数式波形ではなく、現実のセンサーデータに含まれる不完全さを再現する機能を組み込んでいます。
- VCOモード:
generate_signalで周波数を範囲指定(タプル)すると、周波数や振幅がランダムウォークしながら滑らかに変動します(アナログ回路の電圧変動や回転数の揺らぎを模倣)。 - PWM/サイクルモード: 矩形波やのこぎり波では、1サイクルごとに周波数をランダムに切り替えることが可能です。
4. 🧪 間欠的な異常のシミュレーション(FMEA的アプローチ)
すべての加工メソッド(limit, multiply, decay, trend)は、共通のタイミング制御エンジンで動作します。
- Interval & Duration: 「5秒おき(interval)に、1秒間だけ(duration)ゲインが2倍になる(multiply)」といった、間欠的な故障や接触不良を簡単なパラメータで表現できます。
- Delay: 「稼働開始から1時間後にドリフト(trend)が始まる」といった経年劣化のシナリオも
delay引数一つで記述可能です。 現場でよく見る「時々おかしくなるデータ」を意図的に作り出せるのが、このツールの真骨頂です。
5. 🧼 統合管理と出力の簡素化
作成した複数の信号を管理し、分析用データセットへ変換する手間を省きます。
- merge(): 複数の信号(Series)を単純加算して合成波形を作ります。時間軸が統一されているため、ズレを気にする必要はありません。
- create_dataframe():
add()で登録された各信号を一括で結合し、タイムスタンプ付きのpd.DataFrameとして出力します。これにより、即座に可視化やAIモデルの学習データとして利用可能です。
なぜ乱数だけではダメなのか?
異常検知の学習データを作る際、単なる一様乱数は「文脈を持たないノイズ」になりがちです。しかし、実際の故障は「特定の周期で振幅が増大する(multiply + interval)」や「衝撃のあとに波形が減衰する(spike + decay)」といった、物理法則に基づいた挙動として現れます。
SignalComposerは、こうした「物理的な文脈(いつ、どのくらい、どのように変化するか)」をデータに与え、エンジニアのドメイン知識をシミュレーションに反映させるための道具です。
メソッド紹介
SignalComposer には、リアルな時系列信号を生成・加工・合成するための、さまざまなメソッドが搭載されています。 これらを組み合わせることで、単純な波形から複雑な異常シナリオまでを自由に描き出すことができます。
メソッドは大きく分けて、以下の3つのカテゴリに整理できます。
- 信号生成系:サイン波、トレンド、ノイズ、スパイクなど、基本となる波形を生成
- フィルター系:生成した信号に対して、クリッピングや周期的な変調などの加工を適用
- 結合&DataFrame化:複数の信号を合成し、学習や可視化に使いやすい形式に変換
データ生成系(Source)
ゼロから波形を作り出すメソッド群(Generators)です。これらを組み合わせてベースとなる信号を構築します。 このクラスでは、generate_signal という一つの強力なメソッドが、設定(func引数)によって多彩な波形を生み出す設計になっています。
| メソッド名 | 設定 (func/引数) | 役割 | 現実世界のシミュレート例 |
|---|---|---|---|
| generate_signal | func="sin", "cos" | 周期的な曲線波形を作る※generate_curveとしても利用可 | モーターの回転振動、商用電源(50/60Hz)、呼吸や脈拍のような生体信号 |
| func="square", "sawtooth" | 矩形波・のこぎり波を作る | PWM制御信号、カウンタのカウントアップ、定期的なリセット動作 | |
| func="0-F" (Hex文字列)例: "0123...F0" | 任意のパターンを繰り返す | 通信プロトコル、特定の制御シーケンス、複雑な機械動作のサイクル | |
| generate_noise | interval 指定なし | 不規則な変動(ホワイトノイズ)を作る | 電気的な熱雑音、環境ノイズ |
| generate_noise | interval 指定あり | 階段状のランダム変動を作る | 気流の乱れによる温度変化、サンプリング周期の粗いセンサー値 |
| generate_spike | - | 突発的な衝撃(スパイク)を作る | 歯車の欠け、バーストノイズ、回路の短絡、落雷サージ |
import pandas as pd
import matplotlib.pyplot as plt
from datetime import datetime
from SignalComposer import SignalComposer
# 1. コンポーザー初期化
composer = SignalComposer(
start_time=datetime.now(),
sampling_period="100ms",
gen_time="10m",
seed=20260113
)
# ① Sin波 (固定・安定)
vibration_sin = composer.generate_signal(
func="sin",
freq="0.05Hz",
amplitude=2.0,
bias=50.0
)
# ② 矩形波 (周波数と振幅をランダムに)
load_square = composer.generate_signal(
func="cos",
freq=("0.05Hz", "0.2Hz"),
amplitude=(3.0, 7.0),
bias=40.0
)
# ③ Pattern (速度とベース位置をランダムに)
# 16進数文字列を func に渡す
op_pattern = composer.generate_signal(
func="01234478ABCDD4321220",
freq=("0.06Hz", "0.2Hz"), # cycle_timeの代わりにfreq(Hz)で指定
amplitude=(5.0, 15.0),
bias=(60.0, 70.0)
)
# ④ トレンド
temp_base = composer.generate_signal(func="sin", freq="1Hz", amplitude=0)
temperature = composer.trend(temp_base, start=20.0, end=45.0)
# ⑤ スパイク (高さと間隔をランダムに)
impact_spike = composer.generate_spike(
interval=("20s", "60s"),
amplitude=(10.0, 30.0),
bias=5.0
)
# ⑥ ノイズ (振れ幅と間隔をランダムに)
system_noise = composer.generate_noise(
amplitude=(1.0, 4.0),
interval=("100ms", "1s"),
bias=10.0,
delay="30s"
)
# --- 登録 ---
composer.add("Fixed_Sin", vibration_sin)
composer.add("Random_Square", load_square)
composer.add("Random_Pattern", op_pattern)
composer.add("Temperature_Trend", temperature)
composer.add("Random_Spike", impact_spike)
composer.add("Random_Noise", system_noise)
# DataFrame作成
# DataFrame作成までは同じ
df = composer.create_dataframe()
# --- グラフ描画(1つのグラフに重ねる) ---
plt.figure(figsize=(15, 8)) # 横長にして見やすくする
cols = df.columns[1:]
for col in cols:
# alpha=0.7 で少し透過させ、重なりを見やすくする
plt.plot(df["timestamp"], df[col], label=col, alpha=0.7)
# 凡例をグラフの外側(右上)に配置
plt.legend(bbox_to_anchor=(1.01, 1), loc='upper left', borderaxespad=0.)
plt.grid(True, alpha=0.3)
plt.ylabel("Value")
plt.xlabel("Time")
plt.title("Advanced Motor Simulation (Overlaid)")
plt.tight_layout()
plt.show()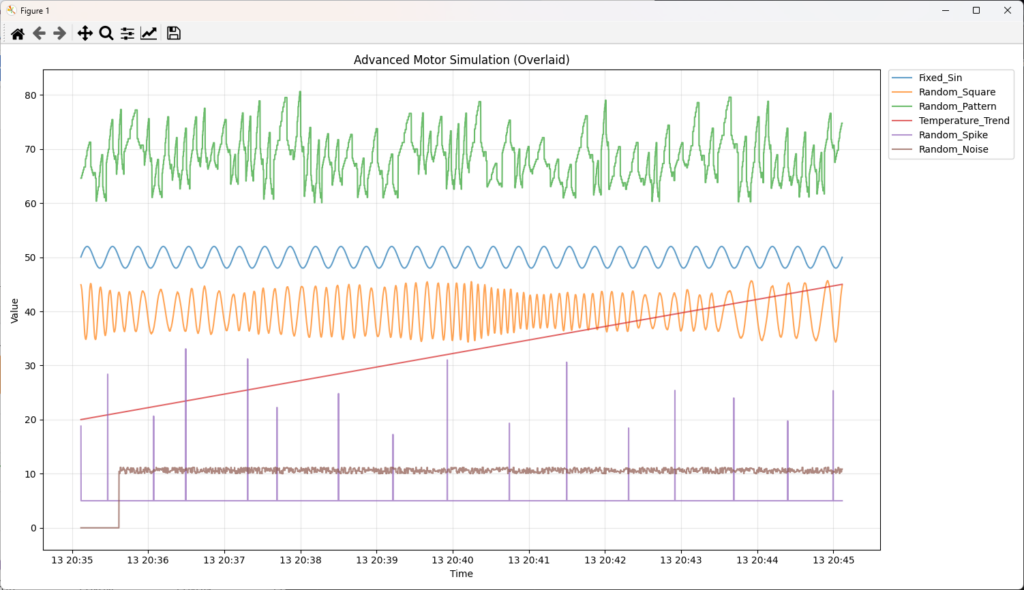
フィルター・加工系(Filter)
生成した信号(Series)を入力とし、物理的な制約や特定の異常現象を付与するメソッド群です。 これらは共通の引数(delay, interval, duration)を持っており、「常時発生」だけでなく「間欠的な故障」や「特定の時間帯だけの異常」を表現できるのが特徴です。
| メソッド名 | 役割 | 現実世界のシミュレート例 |
|---|---|---|
| limit | 上下限で値をカットする(クリッピング) | センサーの飽和(サチレーション)、ADコンバータのレンジオーバー、メカニカルな可動範囲の突き当たり |
| multiply | 値に係数を掛けて増幅/減衰させる | 突発的なゲイン増大、共振による「うねり」、接触不良による信号レベルの低下、(interval指定による)断続的な振動 |
| trend | 直線的な変化(傾き)を加算する | センサーのゼロ点ドリフト、温度上昇に伴うベースラインの移動、機械部品の摩耗による経年変化 |
| decay | 時間経過とともに指数関数的に減衰させる | 衝撃(スパイク)後の残留振動、コンデンサの放電、バネ・ダンパー系の減衰挙動 |
import matplotlib.pyplot as plt
from datetime import datetime
from SignalComposer import SignalComposer
# 1. 初期化
composer = SignalComposer(
start_time=datetime.now(),
sampling_period="100ms",
gen_time="1h"
)
# --- モーターAの回転(サイン波) ---
# sampling_periodは初期化時の設定を使うため削除
vibration_a = composer.generate_signal(
func="sin",
freq="0.001Hz",
amplitude=3.0,
gen_time="1h"
)
# センサーの限界値(2.5)でクリッピング
# limitメソッドを追加したので動作します
vibration_a_limited = composer.limit(vibration_a, upper=2.5, lower=-2.5)
composer.add("motor_a_limited", vibration_a_limited)
# --- モーターBの回転(コサイン波) ---
# generate_curve は存在しないため generate_signal に修正
vibration_b = composer.generate_signal(
func="cos",
freq="0.002Hz",
amplitude=1.0,
gen_time="1h"
)
# 特定周期で増幅
# multiplyメソッドを追加したので動作します
vibration_b_distorted = composer.multiply(
vibration_b,
factor=1.5,
interval="500s",
duration="30s",
delay="0ms"
)
composer.add("motor_b_distorted", vibration_b_distorted)
# --- DataFrame作成 ---
df = composer.create_dataframe()
# --- グラフを重ね合わせて描画 ---
plt.figure(figsize=(12, 6))
for col in df.columns:
if col != "timestamp":
plt.plot(df["timestamp"], df[col], label=col, alpha=0.8)
plt.title("Overlaid Motor Vibrations: Limited vs Distorted")
plt.xlabel("Time")
plt.ylabel("Value")
plt.grid(True, alpha=0.3, linestyle="--")
plt.legend(loc="upper right")
plt.tight_layout()
plt.show()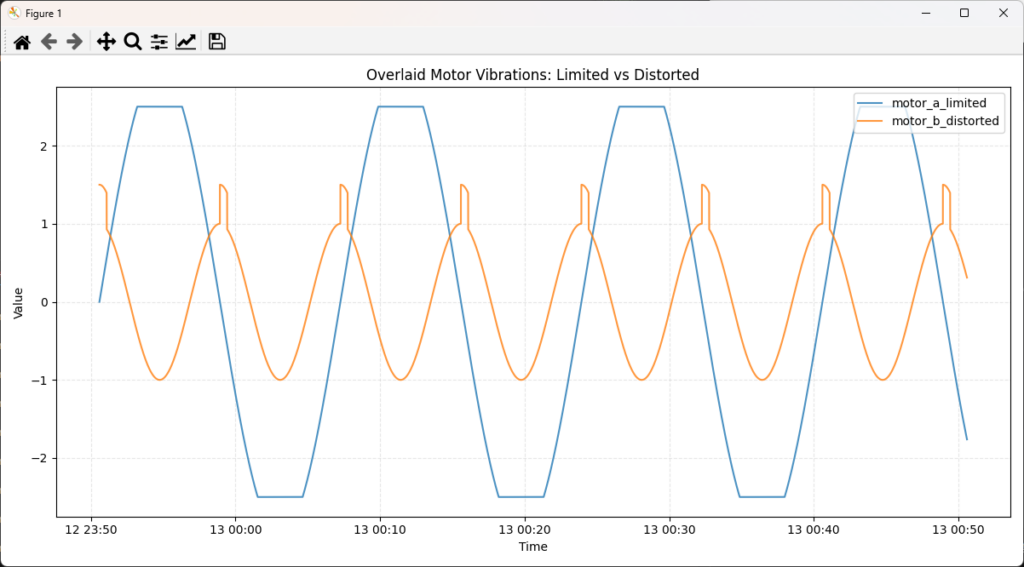
結合・出力系(Composer)
バラバラに作った信号を統合し、解析や保存ができる最終的なデータセット形式(DataFrame)に変換するメソッド群です。
| メソッド名 | 役割 | こだわりポイント |
|---|---|---|
| merge | 複数の信号(Series)を加算合成する | 時間軸の完全一致: 全ての信号は共通のサンプリング周期で生成されているため、補間処理なしで単純加算するだけで、ズレのない合成波形(信号+ノイズ等)が完成します。 |
| add | 信号に名前を付けて内部リストに登録する | 列名の定義: ここで指定した名前("sensor_A", "noise_1"など)が、最終的なDataFrameの「カラム名」として採用されます。 |
| create_dataframe | 登録データをまとめてDataFrame化する | 即戦力のデータ構造: インデックスをリセットし、timestamp カラムを自動生成します。CSV出力や可視化、AIモデルへの入力としてそのまま使える形式で出力されます。 |
import matplotlib.pyplot as plt
from datetime import datetime
from SignalComposer import SignalComposer
# 1. 初期化
composer = SignalComposer(
start_time=datetime.now(),
sampling_period="100ms",
gen_time="10m"
)
# --- 1. トレンドで上昇し続ける波形 ---
# パターン生成
pattern_base = composer.generate_signal(
func="001234567890ABCDEEEEEEEEEAAAAEEEEEEEEEEDCBA098765432100",
freq="0.01Hz",
amplitude=10.0
)
# トレンド生成
base_zeros = composer.generate_signal(func="sin", amplitude=0)
trend_base = composer.trend(base_zeros, start=20.0, end=80.0)
# ノイズ生成
noise_base = composer.generate_noise(
amplitude=(0, 2.0),
interval="500ms"
)
# 合成
rising_wave = pattern_base + trend_base + noise_base
composer.add("上昇トレンド", rising_wave)
# --- 2. 一定期間ごとに収束するサイン波 ---
# ベースとなる連続したサイン波
vibration_base = composer.generate_signal(
func="sin",
freq="0.1Hz",
amplitude=10.0
)
# 減衰処理 (decay)
# 【修正点】
# 1. 引数名を decay_rate → rate に変更
# 2. interval="3m" を指定することで、3分ごとに減衰計算がリセットされ、
# 「減衰して消える→また最大振幅で復活」を繰り返します。
converging_vibration = composer.decay(
vibration_base,
interval="3m", # 3分ごとにリセットして振幅復活
rate=0.99 # 減衰率 (1ステップごとに0.99倍)
)
composer.add("収束サイン波", converging_vibration)
# --- DataFrame作成 ---
df = composer.create_dataframe()
# 確認用プロット
plt.figure(figsize=(12, 6))
plt.plot(df["timestamp"], df["上昇トレンド"], label="Rising Trend", alpha=0.8)
plt.plot(df["timestamp"], df["収束サイン波"], label="Converging Sine", alpha=0.8)
plt.legend()
plt.grid(True, alpha=0.3)
plt.title("Generated Signals")
plt.xlabel("Time") # 軸ラベル追加
plt.tight_layout() # レイアウト調整
plt.show()
print(df.head())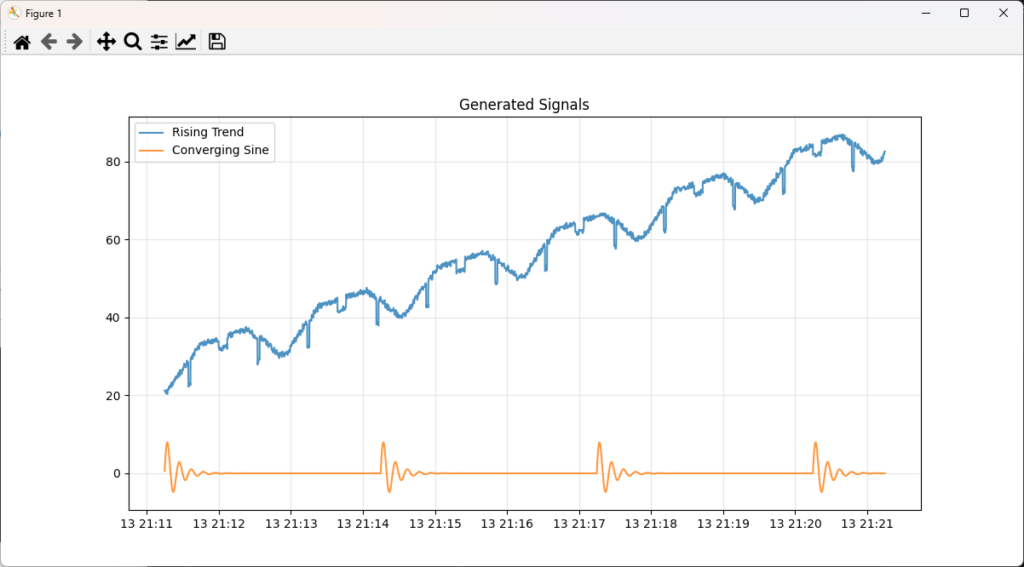
timestamp 上昇トレンド 収束サイン波
0 2026-01-13 21:10:54.110063 21.247099 0.627905
1 2026-01-13 21:10:54.210063 21.257101 1.240799
2 2026-01-13 21:10:54.310063 21.267102 1.836524
3 2026-01-13 21:10:54.410063 21.277104 2.413035
4 2026-01-13 21:10:54.510063 21.287106 2.968405
応用例
定期的なバースト振動の発生シミュレーション
「通常稼働している機械が、ある時点から異常な過負荷や衝撃(バースト的な振動)を定期的に受け始め、それが物理的な限界値を超えて飽和(クリップ)している状態」をシミュレーションしたものです。

import pandas as pd
import matplotlib.pyplot as plt
from datetime import datetime
from SignalComposer import SignalComposer
# 1. 初期化 (100秒間生成)
composer = SignalComposer(
start_time=datetime.now(),
sampling_period="10ms", # 10msサンプリング
gen_time="100s" # 100秒間
)
# 2. ベース波形(きれいなサイン波 5Hz)
# generate_curve を generate_signal に修正
p_base = composer.generate_signal(
func="sin",
freq="5Hz",
amplitude=5.0,
bias=12.0
)
# 3. 50秒後から「1秒ごとに0.2秒間だけ」振幅を2.5倍にする
# これにより、後半から間欠的なパルス状の増幅が発生します
p_gated = composer.multiply(
p_base,
factor=2.5,
interval="1s",
duration="200ms",
delay="50s"
)
# 4. 物理限界を設定(上限18.0でカットして波形を潰す)
p_final = composer.limit(p_gated, upper=18.0)
# --- 信号の登録とデータ出力 ---
composer.add("sensor_value", p_final)
df_output = composer.create_dataframe()
# CSV保存
df_output.to_csv("simulation_data.csv", index=False, encoding='utf-8')
print("CSV出力完了: simulation_data.csv")
# --- グラフ描画 ---
plt.figure(figsize=(15, 6))
plt.plot(df_output["timestamp"], df_output["sensor_value"], label="Sensor Value")
plt.axhline(y=18.0, color='red', linestyle='--', label="Limit (18.0)") # 限界線
plt.title("Sensor Simulation (Limited)")
plt.xlabel("Time")
plt.ylabel("Value")
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()加速走行中に発生した機械的故障シミュレーション
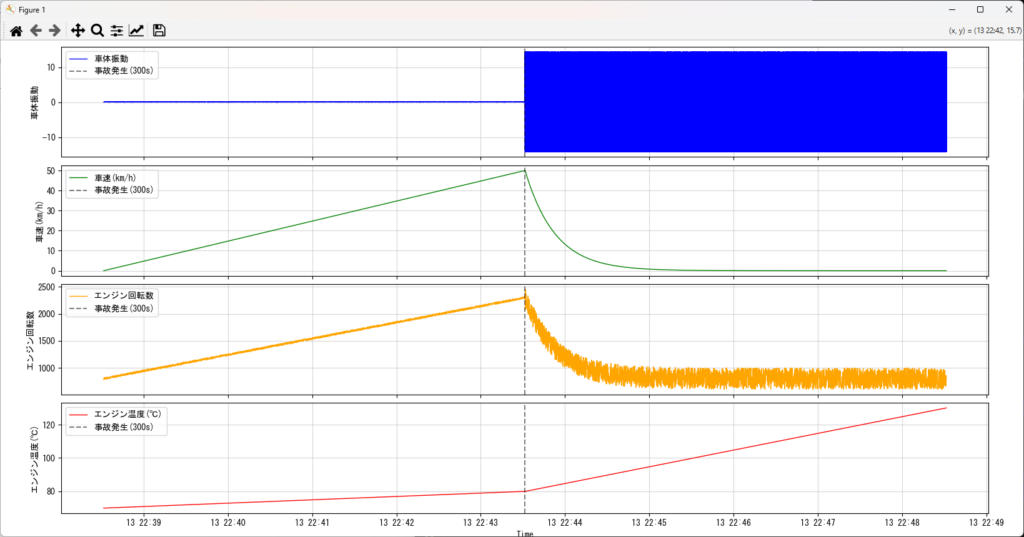
「正常な加速走行中に突如として発生した機械的故障(歯車破損)と、それが車両全体に与える物理的影響」を時系列でシミュレーションしたものです。
シミュレーションのストーリー
- 300秒まで(正常): スムーズに加速し、回転数も温度も安定して上昇しています。
- 300秒時点(事故発生): 歯車が壊れ、激しい「車体振動」が発生します。
- それ以降(連鎖する異常):
- 車速: 駆動ロスにより、アクセルを踏んでいても失速し始めます。
- 回転数: 破損箇所の負荷変動で、針が激しくブレ(不安定化)ます。
- 温度: 内部の異常摩擦により、一気にオーバーヒートへ向かいます。
import matplotlib.pyplot as plt
from datetime import datetime,timedelta
from SignalComposer import SignalComposer
# 1. コンポーザー初期化
# 振動を表現するためサンプリング周期は短め(10ms)推奨
composer = SignalComposer(
start_time=datetime.now(),
sampling_period="10ms",
gen_time="10m"
)
# =========================================================
# シナリオ再現: 300秒(5分)を境に天国から地獄へ
# =========================================================
# --- 【1. 車体振動】 ---
# 正常時: 路面の微細な振動のみ
# 異常時: 300秒で歯車が壊れ、激しい振動(20Hz)が突然発生し継続する
vib_noise = composer.generate_noise(amplitude=(-0.5, 0.5)) # 正常時の微振動
# 異常振動: 20Hzの激しい波形
# delay="5m" で5分後から発生させます
vib_anomaly = composer.generate_signal(
func="sin",
freq="20Hz",
amplitude=15.0,
delay="5m"
)
# 合成
vehicle_vib = vib_noise + vib_anomaly
composer.add("車体振動", vehicle_vib)
# --- 【2. 車速】 ---
# 正常時: スムーズに加速 (0 -> 100km/h)
# 異常時: 駆動ロスにより、アクセルを踏んでいても失速し始める
speed_base = composer.generate_signal(func="sin", amplitude=0) # 0のベース
speed_accel = composer.trend(speed_base, start=0.0, end=100.0) # 加速トレンド
# 5分後から減衰(Decay)を適用して失速させる
# rate=0.9995 で徐々に速度が落ちていく演出
speed_final = composer.decay(
speed_accel,
rate=0.9995,
delay="5m"
)
composer.add("車速(km/h)", speed_final)
# --- 【3. エンジン回転数】 ---
# 正常時: 車速に連動して安定上昇
# 異常時: 負荷変動で針が激しくブレる(ノイズ増大)
# ベース回転数 (車速連動 + アイドリング800rpm)
rpm_base = speed_final * 30 + 800
# ノイズ成分
rpm_noise = composer.generate_noise(level=(-20, 20), interval="100ms")
# 5分後からノイズを10倍に増幅して「激しいブレ」を再現
rpm_noise_unstable = composer.multiply(
rpm_noise,
factor=10.0,
delay="5m"
)
engine_rpm = rpm_base + rpm_noise_unstable
composer.add("エンジン回転数", engine_rpm)
# --- 【4. エンジン温度】 ---
# 正常時: 安定して上昇 (70℃ -> 90℃)
# 異常時: 異常摩擦により一気にオーバーヒートへ (+40℃急上昇)
temp_zeros = composer.generate_signal(func="sin", amplitude=0)
# 正常トレンド
temp_normal = composer.trend(temp_zeros, start=70.0, end=90.0)
# 異常トレンド (5分後から急激に温度を上乗せ)
temp_overheat = composer.trend(
temp_zeros,
start=0.0,
end=40.0, # さらに40度上がる
delay="5m"
)
engine_temp = temp_normal + temp_overheat
composer.add("エンジン温度(℃)", engine_temp)
# =========================================================
# 出力・描画
# =========================================================
df = composer.create_dataframe()
# グラフ描画
fig, axes = plt.subplots(4, 1, figsize=(12, 12), sharex=True)
cols = ["車体振動", "車速(km/h)", "エンジン回転数", "エンジン温度(℃)"]
colors = ["blue", "green", "orange", "red"]
# 300秒(5分)のラインを描画するための設定
fault_time = df["timestamp"].iloc[0] + timedelta(minutes=5)
for ax, col, c in zip(axes, cols, colors):
# 振動データは見やすいようにそのまま、他は少し間引く
step = 1 if col == "車体振動" else 10
ax.plot(df["timestamp"][::step], df[col][::step], label=col, color=c, linewidth=1.0)
# 事故発生タイミングに縦線を入れる
ax.axvline(x=fault_time, color="black", linestyle="--", alpha=0.5, label="事故発生(300s)")
ax.legend(loc="upper left")
ax.grid(True, alpha=0.5)
ax.set_ylabel(col)
plt.xlabel("Time")
plt.tight_layout()
plt.show()SignalComposer クラス リファレンス
初期化
composer = SignalComposer(
start_time=datetime(2025, 1, 1),
sampling_period="100ms",
gen_time="10m",
seed=20260107
)- start_time (
datetime): データ生成の基準となる開始時刻。 - sampling_period (
str|int|float): サンプリング周期。"100ms",0.1(秒),"10Hz"等の指定が可能。 - gen_time (
str|int|float): デフォルトの生成期間。"10m","1h",600(秒) 等。 - seed (
int, optional): 乱数シード。指定することでノイズや揺らぎの再現性を確保します。
信号生成メソッド (Generators)
generate_signal (万能波形生成)
func 引数の指定により、サイン波から任意パターンまで生成可能なメインメソッドです。 ※ generate_curve はこのメソッドのエイリアス(別名)です。
- func (
str): 波形の種類。"sin","cos": 正弦波/余弦波。"square","sawtooth": 矩形波/のこぎり波。- Hexモード:
"0123...F"のような16進数文字列を指定すると、その形状のステップ波形を生成します。
- freq (
str|tuple): 周波数(例:"1Hz","500ms")。- タプル
("0.9Hz", "1.1Hz")で指定すると、周波数が滑らかに揺らぐ VCOモード になります。 - 矩形波等の場合、1サイクルごとに周波数がランダムに変化します。
- タプル
- amplitude (
float|tuple): 振幅。タプル指定で範囲ランダム。 - bias (
float|tuple): 中心値(オフセット)。 - delay (
str): 生成開始を遅らせる時間(例:"5s")。 - phase (
float): 初期位相(ラジアン)。
generate_noise (ノイズ)
ランダムノイズを生成します。
- level (
float|tuple): ノイズの振れ幅。(min, max)で範囲指定も可能。 - interval (
str): 値を保持する期間(例:"1s")。- 指定なし:毎サンプリングごとに変化(ホワイトノイズ)。
- 指定あり:その期間だけ同じ値を維持(階段状ノイズ)。
- delay (
str): 発生開始を遅らせる時間。
generate_spike (突発的な衝撃)
ベースライン(bias)に対し、間欠的なスパイク値を加算します。
delay (str): 最初の発生までの遅延。信号生成メソッド
amplitude (float | tuple): スパイクの高さ(正負可)。
bias (float): ベースとなる値。
interval (str): スパイクが発生する間隔。
信号加工メソッド(Processors)
生成済みの信号(Series)を入力し、物理的な効果を適用して返します。 全ての加工メソッドで、以下の共通引数によるタイミング制御が可能です。
共通制御引数:
- delay (
str): 効果の開始タイミング(例:"10s"後から異常発生)。- interval (
str): 繰り返し間隔(例:"5s"おきに発生)。- duration (
str): 1回の効果継続時間(例:"1s"間だけ異常が続く)。- max_repeats (
int): 繰り返す最大回数。- fill_after (
float): 処理終了後の値を固定する場合に指定。
limit (クリッピング)
値を上下限でカットします。「センサーの飽和」の再現などに使用します。
- upper (
float): 上限値。 - lower (
float): 下限値。
multiply (増幅・減衰)
信号に係数を掛け合わせます。「接触不良(係数0)」や「共振(係数>1)」の再現に使用します。
- factor (
float): 掛け合わせる倍率。
decay (減衰)
指定された期間(duration)の中で、波形を指数関数的に減衰させます。「衝撃後の振動収束」などに最適です。
- rate (
float): 減衰率(0.0~1.0)。1ステップごとの減少割合。intervalを併用すると、減衰効果が周期的にリセットされ、何度も衝撃が起きる様子を再現できます。
trend (トレンド・ドリフト)
波形に直線的な傾きを加算します。「経年劣化」や「温度ドリフト」の再現に使用します。
- start (
float): 加算する直線の開始値。 - end (
float): 加算する直線の終了値。
4. 合成と出力(Management)
merge
- リストで渡された複数の信号(Series)を単純加算します。すべての信号は初期化時の
start_timeとsampling_periodに基づいて生成されているため、自動的に時間軸が整列します。
add / create_dataframe
add(name, series): 信号に列名を付けて登録します。create_dataframe(): 登録された全信号を結合し、timestamp列を持つ pandas DataFrame を生成して返します。
composer.add("Sensor_A", series_a)
df = composer.create_dataframe()信号データを「直感的」に作成できるGUIツール
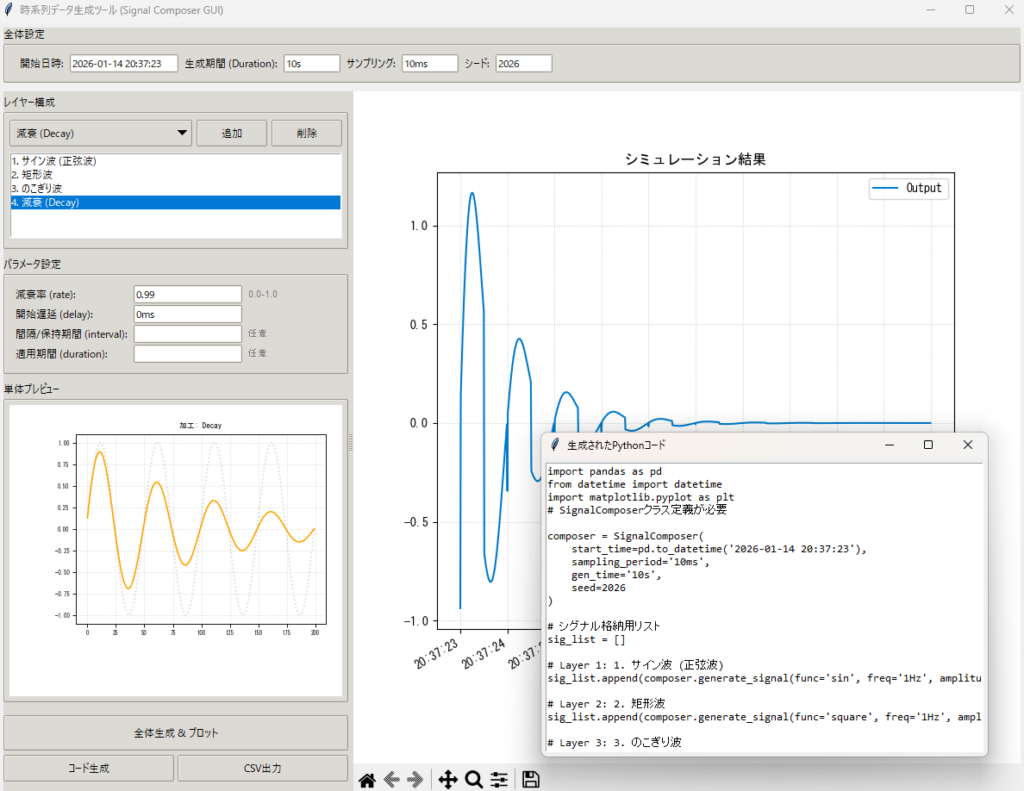
これを使えば、波形のプレビューを見ながらパラメータを変更し、納得した「異常パターン」をレイヤーのように重ねていくことができます。
概要
即時反映のリアルタイム・プレビュー
「周波数 5Hz」「減衰率 0.9」と数値で言われても、実際の波形をイメージするのは困難です。 このツールでは、レイヤーを選択してパラメータ数値を変更するだけで、左下のミニグラフ(オレンジ色)に即座に波形がプレビューされます。ボタンを押す手間もなく、納得いくまで試行錯誤が可能です。
柔軟なレイヤー・プロセッシング
「信号生成(Generator)」と「信号加工(Processor)」をすべて「レイヤー」として統一的に扱います。 リストの上から順に処理が行われるため、以下のような複雑な構成も直感的に作れます。
- Generator(正弦波、ノイズなど): リストに追加され、順次
merge(加算)されます。 - Processor(Limit, Decayなど): **「そこまでに積み上がった信号」**に対して、フィルタ効果を適用します。
- Limit: センサーの飽和(クリッピング)
- Multiply: 突発的なゲイン変動
- Decay/Trend: 減衰やドリフト これらは
delay(開始遅延)やinterval(発生間隔)も指定できるため、「10秒後から、3秒おきに一瞬だけ値が跳ねる」といった挙動もノンコーディングで設定可能です。
リスト蓄積によるシナリオ作成
作成手順はシンプルです。必要な要素をどんどんリストに追加していくだけです。
- ベースの正弦波を追加
- 「Limit」レイヤーを追加(正弦波の頭を潰す)
- その上に「ホワイトノイズ」を追加(潰れた波形の上にノイズが乗る)
最後に**「全体生成&プロット」**ボタンを押すと、SignalComposer の merge 機能によってすべてのレイヤーが正しい順序で計算・統合され、右側のメイングラフ(青色)に完成形が表示されます。
再現用Pythonコードの自動生成
GUIで作った波形が気に入ったら、**「コード生成」**ボタンをクリックしてください。 現在のレイヤー構成を「リスト作成 → merge」という非常にスマートなPythonコードに変換し、別ウィンドウで表示します。これをコピーするだけで、学習用スクリプトなどで即座に再利用可能です。に貼り付けるだけで、すぐにAIの学習データとして利用できます。
使い方の流れ
- レイヤー追加
プルダウンから「サイン波」や「ノイズ」、あるいは「加工処理(Limitなど)」を選び、「追加」ボタンを押します。 - パラメータ調整
追加されたレイヤーを選択し、数値を入力します。変更は即座に左下のプレビューに反映されます。 - 構成の確認
必要に応じてレイヤーを削除したり、さらに追加して重ね合わせます。 - 全体合成
「全体生成&プロット」を押し、すべての信号が合わさった最終形を確認します。 - 出力
必要に応じて「CSV出力」で保存するか、「コード生成」でプログラムとして書き出します。
ソースコード
簡易信号生成UIツール
gen_signal_ui.py という名前で保存してください。
import pandas as pd
import numpy as np
from datetime import datetime, timedelta
import random
import matplotlib.pyplot as plt
from typing import Optional, Tuple, Union, List, Callable
import tkinter as tk
from tkinter import ttk, messagebox, filedialog
from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg, NavigationToolbar2Tk
import ast
# ------------------------------------------------------------------
# フォント設定
# ------------------------------------------------------------------
try:
plt.rcParams['font.family'] = 'MS Gothic'
except:
pass
# ==============================================================================
# 1. SignalComposer クラス (変更なし)
# ==============================================================================
class SignalComposer:
def __init__(
self,
start_time: datetime,
sampling_period: Union[str, int, float] = "100ms",
gen_time: Union[str, int, float] = "10000ms",
seed: Optional[int] = 20260107,
):
self._rng = random.Random(seed)
self._np_rng = np.random.default_rng(seed)
self.start_time = start_time
self.default_sampling_period = self._parse_to_ms(sampling_period)
self.default_gen_time = self._parse_to_ms(gen_time)
self.signals = {}
def _parse_single_to_ms(self, value):
if value is None: return 0
if isinstance(value, (int, float)): return int(float(value) * 1000)
v_str = str(value).lower().strip()
if v_str.endswith('hz'): return int(1000.0 / float(v_str.replace('hz', '')))
try: return int(pd.to_timedelta(v_str).total_seconds() * 1000)
except: return int(float(v_str) * 1000)
def _parse_to_ms(self, value):
if isinstance(value, tuple):
return int(self._rng.uniform(self._parse_single_to_ms(value[0]), self._parse_single_to_ms(value[1])))
return self._parse_single_to_ms(value)
def _resolve_freq_range(self, freq):
def to_hz(f):
s = str(f).lower().strip()
if "hz" in s: return float(s.replace("hz",""))
ms = self._parse_single_to_ms(f)
return 1000.0/ms if ms>0 else 0.0
if isinstance(freq, tuple): return (to_hz(freq[0]), to_hz(freq[1]))
return (to_hz(freq), to_hz(freq))
def _resolve_val(self, val):
if isinstance(val, tuple): return self._rng.uniform(val[0], val[1])
return float(val)
def _resolve_val_range(self, val):
if isinstance(val, tuple): return (val[0], val[1])
return (val, val)
def _create_series(self, values, delay_val="0ms"):
s_period = self.default_sampling_period
ts = [self.start_time + timedelta(milliseconds=i * s_period) for i in range(len(values))]
series = pd.Series(values, index=pd.to_datetime(ts))
delay_ms = self._parse_to_ms(delay_val)
if delay_ms > 0:
shift = int(delay_ms // s_period)
series = series.shift(shift).fillna(0.0)
return series
def _apply_operation(self, series: pd.Series, func: Callable[[pd.Series], pd.Series], delay: str, interval: Optional[str], duration: Optional[str], max_repeats: Optional[int], fill_after: Optional[float]) -> pd.Series:
s = series.copy()
total_len = len(s)
delay_idx = int(self._parse_to_ms(delay) // self.default_sampling_period)
if delay_idx >= total_len: return s
if interval is None:
target_slice = s.iloc[delay_idx:]
if len(target_slice) > 0:
s.iloc[delay_idx:] = func(target_slice)
return s
curr = delay_idx
int_pts = max(1, int(self._parse_to_ms(interval) // self.default_sampling_period))
dur_pts = int(self._parse_to_ms(duration) // self.default_sampling_period) if duration else int_pts
if dur_pts <= 0: dur_pts = 1
count = 0
while curr < total_len:
if max_repeats is not None and count >= max_repeats:
if fill_after is not None: s.iloc[curr:] = fill_after
break
end_win = min(curr + dur_pts, total_len)
target_slice = s.iloc[curr:end_win]
if len(target_slice) > 0:
s.iloc[curr:end_win] = func(target_slice)
curr += int_pts
count += 1
return s
def generate_signal(self, func: str, freq="1Hz", gen_time=None, amplitude=1.0, bias=0.0, delay="0ms", phase=0.0):
s_period = self.default_sampling_period
g_time = self._parse_to_ms(gen_time) or self.default_gen_time
pts_total = int(g_time // s_period)
f = func.lower()
if f in ["sin", "cos"]:
min_hz, max_hz = self._resolve_freq_range(freq)
min_amp, max_amp = self._resolve_val_range(amplitude)
min_bias, max_bias = self._resolve_val_range(bias)
smoothness = 50.0
steps_hz = self._np_rng.uniform(-1, 1, pts_total)
steps_amp = self._np_rng.uniform(-1, 1, pts_total)
curr_hz, curr_amp, curr_bias = (min_hz+max_hz)/2, (min_amp+max_amp)/2, (min_bias+max_bias)/2
dh, da, db = (max_hz-min_hz)/smoothness, (max_amp-min_amp)/smoothness, (max_bias-min_bias)/smoothness
freqs, amps, biases = np.zeros(pts_total), np.zeros(pts_total), np.zeros(pts_total)
for i in range(pts_total):
if dh>0: curr_hz = np.clip(curr_hz + steps_hz[i]*dh, min_hz, max_hz)
freqs[i] = curr_hz
if da>0: curr_amp = np.clip(curr_amp + steps_amp[i]*da, min_amp, max_amp)
amps[i] = curr_amp
if db>0: curr_bias += self._np_rng.uniform(-1,1)*db
biases[i] = curr_bias
dt = s_period / 1000.0
phase_arr = np.cumsum(freqs * dt * 2 * np.pi) + phase
vals = amps * np.sin(phase_arr) if f=="sin" else amps * np.cos(phase_arr)
return self._create_series(vals + biases, delay)
vals = []
hex_map = {c: int(c, 16) for c in "0123456789ABCDEF"}
while len(vals) < pts_total:
c_amp = self._resolve_val(amplitude)
c_bias = self._resolve_val(bias)
min_h, max_h = self._resolve_freq_range(freq)
c_hz = self._rng.uniform(min_h, max_h) or 0.001
if f in ["square", "sawtooth"]:
c_pts = max(1, int((1000.0/c_hz)//s_period))
x = 2*np.pi*c_hz * (np.arange(c_pts)*s_period/1000.0)
w = c_amp * np.sign(np.sin(x)) if f=="square" else c_amp*(2*(x/(2*np.pi)%1)-1)
vals.extend(w + c_bias)
else:
ms_step = (1000.0/c_hz)/len(func)
pts_step = max(1, int(round(ms_step/s_period)))
for char in func:
v = (hex_map.get(char.upper(), 0)/15.0)*c_amp + c_bias
vals.extend([v]*pts_step)
return self._create_series(np.array(vals[:pts_total]), delay)
def generate_noise(self, gen_time=None, level=None, amplitude=1.0, bias=0.0, interval="100ms", delay="0ms"):
s_period = self.default_sampling_period
g_time = self._parse_to_ms(gen_time) or self.default_gen_time
pts_total = int(g_time // s_period)
if level is not None:
if isinstance(level, tuple) and len(level)==2: min_v, max_v = float(level[0]), float(level[1])
else: min_v, max_v = 0.0, float(level)
else:
cur_amp = self._resolve_val(amplitude)
cur_bias = self._resolve_val(bias)
min_v, max_v = cur_bias, cur_bias + cur_amp
vals = []
while len(vals) < pts_total:
v = self._rng.uniform(min_v, max_v)
step = max(1, int(self._parse_to_ms(interval) // s_period))
vals.extend([v] * step)
return self._create_series(np.array(vals[:pts_total]), delay)
def generate_spike(self, gen_time=None, amplitude=1.0, bias=0.0, interval="1s", delay="0ms") -> pd.Series:
s_period = self.default_sampling_period
g_time = self._parse_to_ms(gen_time) or self.default_gen_time
cur_bias = self._resolve_val(bias)
pts_total = int(g_time // s_period)
vals = np.full(pts_total, float(cur_bias))
i = 0
while i < pts_total:
vals[i] += self._resolve_val(amplitude)
step = max(1, int(self._parse_to_ms(interval) // s_period))
i += step
return self._create_series(vals, delay)
def limit(self, series: pd.Series, upper: float = None, lower: float = None, delay: str = "0ms", interval=None, duration=None, max_repeats=None, fill_after=None) -> pd.Series:
operation = lambda s: s.clip(lower=lower, upper=upper)
return self._apply_operation(series, operation, delay, interval, duration, max_repeats, fill_after)
def multiply(self, series: pd.Series, factor: float, delay: str = "0ms", interval=None, duration=None, max_repeats=None, fill_after=None) -> pd.Series:
operation = lambda s: s * factor
return self._apply_operation(series, operation, delay, interval, duration, max_repeats, fill_after)
def decay(self, series: pd.Series, rate: float = 0.9, delay: str = "0ms", interval=None, duration=None, max_repeats=None, fill_after=None) -> pd.Series:
def operation(s):
n = len(s)
steps = np.arange(n)
factors = rate ** steps
return s * factors
return self._apply_operation(series, operation, delay, interval, duration, max_repeats, fill_after)
def trend(self, series: pd.Series, start: float = 0.0, end: float = 1.0, delay: str = "0ms", interval=None, duration=None, max_repeats=None, fill_after=None) -> pd.Series:
def operation(s):
n = len(s)
trend_vals = np.linspace(start, end, n)
return s + trend_vals
return self._apply_operation(series, operation, delay, interval, duration, max_repeats, fill_after)
def merge(self, series_list: List[pd.Series]) -> pd.Series:
if not series_list: return pd.Series()
return sum(series_list)
# ==============================================================================
# 2. Tkinter UI Implementation (Code Generation Added)
# ==============================================================================
class SignalGenApp(tk.Tk):
def __init__(self):
super().__init__()
self.title("時系列データ生成ツール (Signal Composer GUI)")
self.geometry("1200x900")
self.layers = []
self.layer_counter = 0
self.generated_series = None
self.current_preview_job = None
style = ttk.Style()
style.theme_use('clam')
self.param_labels = {
"freq": "周波数 (freq)",
"amplitude": "振幅 (amplitude)",
"bias": "オフセット (bias)",
"phase": "位相 (phase)",
"delay": "開始遅延 (delay)",
"level": "範囲 (min, max)",
"interval": "間隔/保持期間 (interval)",
"duration": "適用期間 (duration)",
"rate": "減衰率 (rate)",
"start": "開始値 (start)",
"end": "終了値 (end)",
"upper": "上限値 (upper)",
"lower": "下限値 (lower)",
"factor": "倍率 (factor)",
"func": "パターン (hex string)",
"max_repeats": "最大繰り返し回数 (max_repeats)",
"fill_after": "終了後の値 (fill_after)"
}
self.create_widgets()
def create_widgets(self):
# Top Settings
top_frame = ttk.LabelFrame(self, text="全体設定", padding=10)
top_frame.pack(fill="x", padx=10, pady=5)
ttk.Label(top_frame, text="開始日時:").pack(side="left", padx=5)
self.start_time_var = tk.StringVar(value=datetime.now().strftime("%Y-%m-%d %H:%M:%S"))
ttk.Entry(top_frame, textvariable=self.start_time_var, width=20).pack(side="left")
ttk.Label(top_frame, text="生成期間 (Duration):").pack(side="left", padx=5)
self.gen_time_var = tk.StringVar(value="10s")
ttk.Entry(top_frame, textvariable=self.gen_time_var, width=10).pack(side="left")
ttk.Label(top_frame, text="サンプリング:").pack(side="left", padx=5)
self.sampling_var = tk.StringVar(value="10ms")
ttk.Entry(top_frame, textvariable=self.sampling_var, width=10).pack(side="left")
ttk.Label(top_frame, text="シード:").pack(side="left", padx=5)
self.seed_var = tk.StringVar(value="2026")
ttk.Entry(top_frame, textvariable=self.seed_var, width=10).pack(side="left")
# Main Layout
paned = ttk.PanedWindow(self, orient="horizontal")
paned.pack(fill="both", expand=True, padx=10, pady=5)
left_panel = ttk.Frame(paned)
paned.add(left_panel, weight=1)
right_panel = ttk.Frame(paned)
paned.add(right_panel, weight=3)
# Layer Management
layer_group = ttk.LabelFrame(left_panel, text="レイヤー構成", padding=5)
layer_group.pack(fill="x", expand=False, pady=5)
btn_frame = ttk.Frame(layer_group)
btn_frame.pack(fill="x", pady=2)
self.layer_type_var = tk.StringVar(value="サイン波 (正弦波)")
self.type_map = {
"サイン波 (正弦波)": "Sine Wave",
"矩形波": "Square Wave",
"のこぎり波": "Sawtooth",
"任意パターン(HEX)": "Hex Pattern",
"ノイズ": "Noise",
"スパイク (突出値)": "Spike",
"--- 加工処理 ---": "---",
"リミット (Clip)": "Limit (Clip)",
"ゲイン (倍率)": "Multiply (Gain)",
"減衰 (Decay)": "Decay",
"トレンド (Trend)": "Trend"
}
layer_options = list(self.type_map.keys())
type_menu = ttk.OptionMenu(btn_frame, self.layer_type_var, layer_options[0], *layer_options)
type_menu.pack(side="left", fill="x", expand=True)
ttk.Button(btn_frame, text="追加", command=self.add_layer).pack(side="left", padx=5)
ttk.Button(btn_frame, text="削除", command=self.remove_layer).pack(side="left")
self.layer_list = tk.Listbox(layer_group, height=6, selectmode="single")
self.layer_list.pack(fill="x", expand=False, pady=5)
self.layer_list.bind('<<ListboxSelect>>', self.on_layer_select)
# Param Editor
self.param_frame = ttk.LabelFrame(left_panel, text="パラメータ設定", padding=10)
self.param_frame.pack(fill="x", expand=False, pady=5)
self.param_container = ttk.Frame(self.param_frame)
self.param_container.pack(fill="x", expand=True)
# Preview
preview_frame = ttk.LabelFrame(left_panel, text="単体プレビュー", padding=5)
preview_frame.pack(fill="both", expand=True, pady=5)
self.preview_fig, self.preview_ax = plt.subplots(figsize=(3, 2), dpi=80)
self.preview_fig.subplots_adjust(left=0.2, bottom=0.25, right=0.95, top=0.9)
self.preview_canvas = FigureCanvasTkAgg(self.preview_fig, master=preview_frame)
self.preview_canvas.draw()
self.preview_canvas.get_tk_widget().pack(fill="both", expand=True)
# Actions
action_frame = ttk.Frame(left_panel)
action_frame.pack(fill="x", pady=10)
ttk.Button(action_frame, text="全体生成 & プロット", command=self.run_simulation).pack(fill="x", ipady=5)
# ★ 追加ボタン
sub_action_frame = ttk.Frame(action_frame)
sub_action_frame.pack(fill="x", pady=5)
ttk.Button(sub_action_frame, text="コード生成", command=self.generate_and_show_code).pack(side="left", fill="x", expand=True, padx=(0, 2))
ttk.Button(sub_action_frame, text="CSV出力", command=self.export_csv).pack(side="left", fill="x", expand=True, padx=(2, 0))
# Plot
self.fig, self.ax = plt.subplots(figsize=(5, 4), dpi=100)
self.canvas = FigureCanvasTkAgg(self.fig, master=right_panel)
self.canvas.draw()
toolbar = NavigationToolbar2Tk(self.canvas, right_panel)
toolbar.update()
self.canvas.get_tk_widget().pack(side="top", fill="both", expand=True)
# Param Defs
self.param_defs = {
"Sine Wave": [("func", "sin", "hidden"), ("freq", "1Hz", "例: 1Hz, (1Hz,5Hz)"), ("amplitude", "1.0", "例: 1.0, (0.5, 1.5)"), ("bias", "0.0", ""), ("phase", "0.0", ""), ("delay", "0ms", "")],
"Square Wave": [("func", "square", "hidden"), ("freq", "1Hz", ""), ("amplitude", "1.0", ""), ("bias", "0.0", ""), ("delay", "0ms", "")],
"Sawtooth": [("func", "sawtooth", "hidden"), ("freq", "1Hz", ""), ("amplitude", "1.0", ""), ("bias", "0.0", ""), ("delay", "0ms", "")],
"Hex Pattern": [("func", "0123456789ABCDEF", "Hex文字列"), ("freq", "1Hz", ""), ("amplitude", "1.0", ""), ("bias", "0.0", ""), ("delay", "0ms", "")],
"Noise": [("amplitude", "1.0", ""), ("bias", "0.0", ""), ("level", "", "範囲直接指定 (min,max)"), ("interval", "100ms", "保持期間"), ("delay", "0ms", "")],
"Spike": [("amplitude", "5.0", ""), ("bias", "0.0", ""), ("interval", "1s", ""), ("delay", "0ms", "")],
"Limit (Clip)": [("upper", "1.5", ""), ("lower", "-1.5", ""), ("delay", "0ms", ""), ("interval", "", "任意"), ("duration", "", "任意"), ("max_repeats", "", "繰り返し回数"), ("fill_after", "", "終了後の値")],
"Multiply (Gain)": [("factor", "2.0", ""), ("delay", "0ms", ""), ("interval", "", "任意"), ("duration", "", "任意"), ("max_repeats", "", "繰り返し回数"), ("fill_after", "", "終了後の値")],
"Decay": [("rate", "0.99", "0.0-1.0"), ("delay", "0ms", ""), ("interval", "", "任意"), ("duration", "", "任意"), ("max_repeats", "", "繰り返し回数"), ("fill_after", "", "終了後の値")],
"Trend": [("start", "0.0", ""), ("end", "5.0", ""), ("delay", "0ms", ""), ("interval", "", "任意"), ("duration", "", "任意"), ("max_repeats", "", "繰り返し回数"), ("fill_after", "", "終了後の値")],
}
def add_layer(self):
display_name = self.layer_type_var.get()
l_type = self.type_map.get(display_name, "")
if "---" in display_name: return
params = {}
if l_type in self.param_defs:
for p_def in self.param_defs[l_type]:
key, default, _ = p_def
params[key] = default
self.layer_counter += 1
name = f"{self.layer_counter}. {display_name}"
layer_obj = {"id": self.layer_counter, "type": l_type, "display_name": name, "params": params}
self.layers.append(layer_obj)
self.layer_list.insert(tk.END, name)
self.layer_list.selection_clear(0, tk.END)
self.layer_list.selection_set(tk.END)
self.on_layer_select(None)
def remove_layer(self):
sel = self.layer_list.curselection()
if not sel: return
idx = sel[0]
self.layer_list.delete(idx)
self.layers.pop(idx)
for widget in self.param_container.winfo_children(): widget.destroy()
self.preview_ax.clear()
self.preview_canvas.draw()
def on_layer_select(self, event):
sel = self.layer_list.curselection()
if not sel: return
idx = sel[0]
layer = self.layers[idx]
for widget in self.param_container.winfo_children(): widget.destroy()
defs = self.param_defs.get(layer["type"], [])
row = 0
for p_def in defs:
key, default, tooltip = p_def
if tooltip == "hidden": continue
label_text = self.param_labels.get(key, key)
ttk.Label(self.param_container, text=f"{label_text}:").grid(row=row, column=0, sticky="w", pady=2)
val = layer["params"].get(key, default)
var = tk.StringVar(value=str(val))
def make_updater(k, v_var): return lambda *args: self.on_param_change(idx, k, v_var.get())
var.trace_add("write", make_updater(key, var))
ttk.Entry(self.param_container, textvariable=var).grid(row=row, column=1, sticky="ew", padx=5)
if tooltip: ttk.Label(self.param_container, text=tooltip, font=("Arial", 8), foreground="gray").grid(row=row, column=2, sticky="w")
row += 1
self.update_preview_graph(layer)
def on_param_change(self, layer_idx, key, value):
if layer_idx < len(self.layers):
self.layers[layer_idx]["params"][key] = value
if self.current_preview_job: self.after_cancel(self.current_preview_job)
self.current_preview_job = self.after(100, lambda: self.update_preview_graph(self.layers[layer_idx]))
def parse_param_value(self, val_str):
if not val_str or val_str == "": return None
if isinstance(val_str, tuple): return val_str
if "," in val_str and "(" not in val_str:
parts = val_str.split(",")
return (parts[0].strip(), parts[1].strip())
try: return float(val_str)
except ValueError: pass
try:
t = ast.literal_eval(val_str)
if isinstance(t, tuple): return t
except: pass
return val_str
def update_preview_graph(self, layer):
self.preview_ax.clear()
l_type = layer["type"]
raw_params = layer["params"]
clean_params = {}
for k, v in raw_params.items(): clean_params[k] = self.parse_param_value(v)
try:
preview_composer = SignalComposer(start_time=datetime.now(), sampling_period="10ms", gen_time="2s", seed=42)
except: return
preview_series = None
processors = ["Limit (Clip)", "Multiply (Gain)", "Decay", "Trend"]
try:
if l_type in processors:
base_sig = preview_composer.generate_signal(func="sin", freq="2Hz", amplitude=1.0)
if "Limit" in l_type: preview_series = preview_composer.limit(base_sig, **clean_params)
elif "Multiply" in l_type: preview_series = preview_composer.multiply(base_sig, **clean_params)
elif "Decay" in l_type: preview_series = preview_composer.decay(base_sig, **clean_params)
elif "Trend" in l_type: preview_series = preview_composer.trend(base_sig, **clean_params)
self.preview_ax.plot(base_sig.values, color="gray", alpha=0.3, linestyle=":", label="元波形")
self.preview_ax.set_title(f"加工: {l_type}", fontsize=8)
else:
if "Noise" in l_type: preview_series = preview_composer.generate_noise(**clean_params)
elif "Spike" in l_type: preview_series = preview_composer.generate_spike(**clean_params)
else: preview_series = preview_composer.generate_signal(**clean_params)
self.preview_ax.set_title(f"生成: {l_type}", fontsize=8)
if preview_series is not None:
self.preview_ax.plot(preview_series.values, color="orange", linewidth=1.5)
self.preview_ax.grid(True, linestyle=":", alpha=0.5)
self.preview_ax.tick_params(labelsize=6)
self.preview_canvas.draw()
except Exception: pass
def run_simulation(self):
# レイヤーが無い場合は何もしない
if not self.layers:
messagebox.showwarning("警告", "レイヤーがありません。")
return
try:
st = pd.to_datetime(self.start_time_var.get())
except:
st = datetime.now()
try: seed_val = int(self.seed_var.get())
except: seed_val = None
composer = SignalComposer(
start_time=st,
sampling_period=self.sampling_var.get(),
gen_time=self.gen_time_var.get(),
seed=seed_val
)
processors = ["Limit (Clip)", "Multiply (Gain)", "Decay", "Trend"]
# ★ここが変更点: シグナルを貯めるリスト
sig_list = []
try:
for layer in self.layers:
l_type = layer["type"]
clean_params = {k: self.parse_param_value(v) for k, v in layer["params"].items()}
if l_type in processors:
# 加工処理が来たら、一旦そこまでのリストを結合(merge)して適用する
# 1. 結合
merged_sig = composer.merge(sig_list)
# 2. 加工
if "Limit" in l_type: processed_sig = composer.limit(merged_sig, **clean_params)
elif "Multiply" in l_type: processed_sig = composer.multiply(merged_sig, **clean_params)
elif "Decay" in l_type: processed_sig = composer.decay(merged_sig, **clean_params)
elif "Trend" in l_type: processed_sig = composer.trend(merged_sig, **clean_params)
# 3. リストを「加工済み信号1つ」の状態にリセット
sig_list = [processed_sig]
else:
# Generatorなら、単にリストに追加するだけ
if "Noise" in l_type: new_sig = composer.generate_noise(**clean_params)
elif "Spike" in l_type: new_sig = composer.generate_spike(**clean_params)
else: new_sig = composer.generate_signal(**clean_params)
sig_list.append(new_sig)
# 最後にすべてを結合して完成
self.generated_series = composer.merge(sig_list)
# Plot
self.ax.clear()
if not self.generated_series.empty:
self.ax.plot(self.generated_series.index, self.generated_series.values, label="Output", color="#007acc")
self.ax.set_title("シミュレーション結果")
self.ax.grid(True, linestyle=":", alpha=0.6)
self.ax.legend()
self.fig.autofmt_xdate()
else:
self.ax.text(0.5, 0.5, "データが空です", ha='center', va='center')
self.canvas.draw()
except Exception as e:
messagebox.showerror("エラー", f"{e}")
import traceback
traceback.print_exc()
def export_csv(self):
if self.generated_series is None:
messagebox.showwarning("警告", "データがまだ生成されていません。")
return
path = filedialog.asksaveasfilename(defaultextension=".csv", filetypes=[("CSV Files", "*.csv")])
if path:
df = self.generated_series.reset_index()
df.columns = ["timestamp", "value"]
df.to_csv(path, index=False)
messagebox.showinfo("成功", f"保存しました: {path}")
# ==============================================================================
# コード生成機能(リスト蓄積・マージ型)
# ==============================================================================
def generate_and_show_code(self):
"""現在のGUI設定から、リストとmergeを使ったPythonコードを生成する"""
if not self.layers:
messagebox.showwarning("警告", "レイヤーがありません。")
return
code_lines = []
code_lines.append("import pandas as pd")
code_lines.append("from datetime import datetime")
code_lines.append("import matplotlib.pyplot as plt")
code_lines.append("# SignalComposerクラス定義が必要")
code_lines.append("")
s_time_str = self.start_time_var.get()
samp_str = self.sampling_var.get()
gen_str = self.gen_time_var.get()
seed_str = self.seed_var.get()
code_lines.append(f"composer = SignalComposer(")
code_lines.append(f" start_time=pd.to_datetime('{s_time_str}'),")
code_lines.append(f" sampling_period='{samp_str}',")
code_lines.append(f" gen_time='{gen_str}',")
if seed_str: code_lines.append(f" seed={seed_str}")
code_lines.append(")")
code_lines.append("")
# ★リスト定義
code_lines.append("# シグナル格納用リスト")
code_lines.append("sig_list = []")
code_lines.append("")
processors = ["Limit (Clip)", "Multiply (Gain)", "Decay", "Trend"]
for i, layer in enumerate(self.layers):
l_type = layer["type"]
display_name = layer["display_name"]
# パラメータを処理: Noneや空文字列を除外
parsed_params = {}
for k, v in layer["params"].items():
parsed_val = self.parse_param_value(v)
# None、空文字列、"0ms"(delayのデフォルト)以外を含める
if parsed_val is not None and parsed_val != "":
parsed_params[k] = parsed_val
p_args = ", ".join([f"{k}={repr(v)}" for k, v in parsed_params.items()])
code_lines.append(f"# Layer {i+1}: {display_name}")
if l_type in processors:
# Processorの場合は、merge -> process -> reset list
code_lines.append("# ここまでの信号を結合してフィルタ適用")
code_lines.append("merged = composer.merge(sig_list)")
if "Limit" in l_type:
code_lines.append(f"processed = composer.limit(merged, {p_args})")
elif "Multiply" in l_type:
code_lines.append(f"processed = composer.multiply(merged, {p_args})")
elif "Decay" in l_type:
code_lines.append(f"processed = composer.decay(merged, {p_args})")
elif "Trend" in l_type:
code_lines.append(f"processed = composer.trend(merged, {p_args})")
code_lines.append("sig_list = [processed]")
else:
# Generatorの場合は、単に append するだけ
method = "generate_signal"
if "Noise" in l_type: method = "generate_noise"
elif "Spike" in l_type: method = "generate_spike"
code_lines.append(f"sig_list.append(composer.{method}({p_args}))")
code_lines.append("")
code_lines.append("# 最終結合")
code_lines.append("final_series = composer.merge(sig_list)")
code_lines.append("")
code_lines.append("# プロット")
code_lines.append("if not final_series.empty:")
code_lines.append(" plt.figure(figsize=(10, 5))")
code_lines.append(" plt.plot(final_series.index, final_series.values)")
code_lines.append(" plt.title('Generated Signal')")
code_lines.append(" plt.grid(True)")
code_lines.append(" plt.show()")
code_lines.append("else:")
code_lines.append(" print('No data generated')")
final_code = "\n".join(code_lines)
self.show_code_window(final_code)
def show_code_window(self, code_text):
win = tk.Toplevel(self)
win.title("生成されたPythonコード")
win.geometry("600x500")
text_area = tk.Text(win, wrap="none", font=("Consolas", 10))
text_area.pack(expand=True, fill="both", padx=5, pady=5)
text_area.insert("1.0", code_text)
# コピーボタン
def copy_to_clipboard():
self.clipboard_clear()
self.clipboard_append(text_area.get("1.0", tk.END))
messagebox.showinfo("コピー", "コードをクリップボードにコピーしました")
btn_frame = ttk.Frame(win)
btn_frame.pack(fill="x", pady=5)
ttk.Button(btn_frame, text="クリップボードにコピー", command=copy_to_clipboard).pack(side="right", padx=10)
if __name__ == "__main__":
app = SignalGenApp()
app.mainloop()信号生成クラスソースコード
SignalComposer.py という名前で保存してください。
import pandas as pd
import numpy as np
from datetime import datetime, timedelta
import random
import matplotlib.pyplot as plt
from typing import Optional, Tuple, Union, List, Callable
# ------------------------------------------------------------------
# グラフ描画用の日本語フォント設定
# ※実行環境に合わせてフォント名を変更してください
# Windows: 'MS Gothic' / Mac: 'Hiragino Sans' / Linux: 'IPAGothic' など
# ------------------------------------------------------------------
try:
plt.rcParams['font.family'] = 'MS Gothic'
except:
pass
class SignalComposer:
"""
時系列データの生成・合成・加工を行う統合クラス。
異常検知AIの学習データ作成、IoTセンサーの故障シミュレーション、
物理挙動のモデリングなどをプログラム上で柔軟に行うために設計されています。
【設計思想】
- 生成 (Generate): 基本波形やノイズを生み出します。
- 加工 (Process): 共通化されたタイミング制御エンジンを用いて、
「いつ」「どの間隔で」「どのくらいの間」演算を適用するかを制御します。
【主な機能】
1. 基本波形生成:
- Sin/Cos (VCOモード対応: 周波数の滑らかな揺らぎ)
- 矩形波/のこぎり波/任意パターン (PWMモード対応)
2. ノイズ・異常付与:
- ホワイトノイズ、階段状ノイズ、間欠的なスパイク
3. 信号加工 (DSP的処理):
- limit: クリップ(センサーのサチレーション等)
- multiply: ゲイン調整(突発的な振幅増大等)
- trend: トレンド付与(ドリフト等)
- decay: 減衰処理(衝撃波形や経年劣化)
4. 統合出力:
- 複数信号の合成 (merge)
- Timestamp付きDataFrameへの一括変換
"""
def __init__(
self,
start_time: datetime,
sampling_period: Union[str, int, float] = "100ms",
gen_time: Union[str, int, float] = "10000ms",
seed: Optional[int] = 20260107,
):
"""
SignalComposerを初期化します。
Args:
start_time (datetime): データ生成の開始時刻。
sampling_period (Union[str, int, float]): サンプリング周期(例: "100ms", 0.1)。デフォルト "100ms"。
gen_time (Union[str, int, float]): 生成するデータの総期間(例: "10m", 600)。デフォルト "10000ms"。
seed (Optional[int]): 乱数シード。指定することで再現性のあるランダム波形を生成できます。
"""
self._rng = random.Random(seed)
self._np_rng = np.random.default_rng(seed)
self.start_time = start_time
self.default_sampling_period = self._parse_to_ms(sampling_period)
self.default_gen_time = self._parse_to_ms(gen_time)
self.signals = {}
# =========================================================================
# Internal Utilities (内部処理用ヘルパーメソッド)
# =========================================================================
def _parse_single_to_ms(self, value):
"""単一の値をミリ秒(int)に変換します。Hz指定やtimedelta文字列にも対応。"""
if value is None: return 0
if isinstance(value, (int, float)): return int(float(value) * 1000)
v_str = str(value).lower().strip()
if v_str.endswith('hz'): return int(1000.0 / float(v_str.replace('hz', '')))
try: return int(pd.to_timedelta(v_str).total_seconds() * 1000)
except: return int(float(v_str) * 1000)
def _parse_to_ms(self, value):
"""値またはタプル(範囲)を解析し、ミリ秒単位の数値を返します。範囲の場合はランダム選択します。"""
if isinstance(value, tuple):
return int(self._rng.uniform(self._parse_single_to_ms(value[0]), self._parse_single_to_ms(value[1])))
return self._parse_single_to_ms(value)
def _resolve_freq_range(self, freq):
"""周波数指定を解析し、(min_hz, max_hz) のタプル形式で返します。"""
def to_hz(f):
s = str(f).lower().strip()
if "hz" in s: return float(s.replace("hz",""))
ms = self._parse_single_to_ms(f)
return 1000.0/ms if ms>0 else 0.0
if isinstance(freq, tuple): return (to_hz(freq[0]), to_hz(freq[1]))
return (to_hz(freq), to_hz(freq))
def _resolve_val(self, val):
"""値または範囲タプルから、単一のfloat値を決定します。"""
if isinstance(val, tuple): return self._rng.uniform(val[0], val[1])
return float(val)
def _resolve_val_range(self, val):
"""値または範囲タプルを、(min, max) のタプル形式で返します。"""
if isinstance(val, tuple): return (val[0], val[1])
return (val, val)
def _create_series(self, values, delay_val="0ms"):
"""Numpy配列をPandas Seriesに変換し、必要に応じて開始時間をシフトします。"""
s_period = self.default_sampling_period
ts = [self.start_time + timedelta(milliseconds=i * s_period) for i in range(len(values))]
series = pd.Series(values, index=pd.to_datetime(ts))
delay_ms = self._parse_to_ms(delay_val)
if delay_ms > 0:
shift = int(delay_ms // s_period)
series = series.shift(shift).fillna(0.0)
return series
# =========================================================================
# Core Processing Engine (共通演算エンジン)
# =========================================================================
def _apply_operation(
self,
series: pd.Series,
func: Callable[[pd.Series], pd.Series],
delay: str,
interval: Optional[str],
duration: Optional[str],
max_repeats: Optional[int],
fill_after: Optional[float]
) -> pd.Series:
"""
全ての加工メソッド(limit, multiply, trend, decay)の裏側で動く共通処理エンジン。
指定されたタイミング(Delay, Interval, Duration)に基づいて、
渡された関数 func を適用します。
このメソッドにより、「間欠的なクリッピング」や「周期的なトレンドリセット」といった
複雑な挙動を統一的なインターフェースで実現しています。
"""
s = series.copy()
total_len = len(s)
delay_idx = int(self._parse_to_ms(delay) // self.default_sampling_period)
# 遅延時間がデータ長を超えている場合は何もしない
if delay_idx >= total_len:
return s
# A. 全体適用モード (interval指定なし)
# delay以降、最後まで一括で適用します。
if interval is None:
target_slice = s.iloc[delay_idx:]
if len(target_slice) > 0:
s.iloc[delay_idx:] = func(target_slice)
return s
# B. 間欠/周期適用モード
# intervalごとにdurationの間だけ適用する処理を繰り返します。
curr = delay_idx
int_pts = max(1, int(self._parse_to_ms(interval) // self.default_sampling_period))
# duration未指定ならintervalと同じにする(隙間なく連続させる意図とみなす)
dur_pts = int(self._parse_to_ms(duration) // self.default_sampling_period) if duration else int_pts
if dur_pts <= 0: dur_pts = 1
count = 0
while curr < total_len:
# 最大繰り返し回数チェック
if max_repeats is not None and count >= max_repeats:
# 繰り返し終了後の埋め処理(指定がある場合)
if fill_after is not None:
s.iloc[curr:] = fill_after
break
# 適用ウィンドウの決定(配列外参照防止のmin)
end_win = min(curr + dur_pts, total_len)
# 演算関数の適用
target_slice = s.iloc[curr:end_win]
if len(target_slice) > 0:
s.iloc[curr:end_win] = func(target_slice)
# 次のサイクルへ進む
curr += int_pts
count += 1
return s
# =========================================================================
# Signal Generation (信号生成)
# =========================================================================
def generate_signal(self, func: str, freq="1Hz", gen_time=None, amplitude=1.0, bias=0.0, delay="0ms", phase=0.0):
"""
メインの波形生成メソッド。funcの指定により挙動が切り替わります。
Args:
func (str): 生成する波形の種類。
- "sin", "cos": 連続的な波形。freqを範囲指定(タプル)すると、周波数が滑らかに揺らぐVCOモードになります。
- "square", "sawtooth": 矩形波/のこぎり波。freq範囲指定時は1サイクルごとに周波数がランダムに変わります。
- "0-F"のHex文字列 (例: "0123..."): 任意のパターン生成。
freq (Union[str, float, Tuple]): 周波数(例: "10Hz", "100ms")。タプル指定でランダム範囲となります。
gen_time (Union[str, int]): 生成期間。指定がない場合は初期化時の設定を使用します。
amplitude (Union[float, Tuple]): 振幅。タプル指定で範囲ランダム。
bias (Union[float, Tuple]): 中心値(オフセット)。タプル指定で範囲ランダム。
delay (Union[str, int]): 生成開始を遅らせる時間。
phase (float): 初期位相(ラジアン)。
Returns:
pd.Series: 生成された時系列データ(DatetimeIndex)。
"""
s_period = self.default_sampling_period
g_time = self._parse_to_ms(gen_time) or self.default_gen_time
pts_total = int(g_time // s_period)
f = func.lower()
# A. Sin/Cos (VCO Mode: 滑らかな周波数変動)
if f in ["sin", "cos"]:
min_hz, max_hz = self._resolve_freq_range(freq)
min_amp, max_amp = self._resolve_val_range(amplitude)
min_bias, max_bias = self._resolve_val_range(bias)
# 周波数・振幅をランダムウォークさせて「揺らぎ」を作る
smoothness = 50.0
steps_hz = self._np_rng.uniform(-1, 1, pts_total)
steps_amp = self._np_rng.uniform(-1, 1, pts_total)
curr_hz, curr_amp, curr_bias = (min_hz+max_hz)/2, (min_amp+max_amp)/2, (min_bias+max_bias)/2
dh, da, db = (max_hz-min_hz)/smoothness, (max_amp-min_amp)/smoothness, (max_bias-min_bias)/smoothness
freqs, amps, biases = np.zeros(pts_total), np.zeros(pts_total), np.zeros(pts_total)
for i in range(pts_total):
if dh>0: curr_hz = np.clip(curr_hz + steps_hz[i]*dh, min_hz, max_hz)
freqs[i] = curr_hz
if da>0: curr_amp = np.clip(curr_amp + steps_amp[i]*da, min_amp, max_amp)
amps[i] = curr_amp
if db>0: curr_bias += self._np_rng.uniform(-1,1)*db
biases[i] = curr_bias
dt = s_period / 1000.0
# 周波数の積分により位相を計算(これにより周波数が変化しても波形が千切れない)
phase_arr = np.cumsum(freqs * dt * 2 * np.pi) + phase
vals = amps * np.sin(phase_arr) if f=="sin" else amps * np.cos(phase_arr)
return self._create_series(vals + biases, delay)
# B. Cycle Mode (Square/Sawtooth/Hex: サイクルごとの動的更新)
vals = []
hex_map = {c: int(c, 16) for c in "0123456789ABCDEF"}
while len(vals) < pts_total:
c_amp = self._resolve_val(amplitude)
c_bias = self._resolve_val(bias)
min_h, max_h = self._resolve_freq_range(freq)
c_hz = self._rng.uniform(min_h, max_h) or 0.001
if f in ["square", "sawtooth"]:
c_pts = max(1, int((1000.0/c_hz)//s_period))
x = 2*np.pi*c_hz * (np.arange(c_pts)*s_period/1000.0)
w = c_amp * np.sign(np.sin(x)) if f=="square" else c_amp*(2*(x/(2*np.pi)%1)-1)
vals.extend(w + c_bias)
else:
ms_step = (1000.0/c_hz)/len(func)
pts_step = max(1, int(round(ms_step/s_period)))
for char in func:
v = (hex_map.get(char.upper(), 0)/15.0)*c_amp + c_bias
vals.extend([v]*pts_step)
return self._create_series(np.array(vals[:pts_total]), delay)
# 互換性のためのエイリアス
generate_curve = generate_signal
def generate_noise(self, gen_time=None, level=None, amplitude=1.0, bias=0.0, interval="100ms", delay="0ms"):
"""
ランダムノイズを生成します。
Args:
level (Tuple): (min, max) で値の範囲を直接指定する場合に使用します。
interval (str): 値を保持する期間。これを長くすると「階段状のランダム値」になります。
amplitude (Union[float, Tuple]): ノイズの振れ幅(level未指定時)。
bias (Union[float, Tuple]): ノイズの中心値(level未指定時)。
"""
s_period = self.default_sampling_period
g_time = self._parse_to_ms(gen_time) or self.default_gen_time
pts_total = int(g_time // s_period)
# level=(min, max) が指定された場合の対応
if level is not None:
if isinstance(level, tuple) and len(level)==2:
min_v, max_v = float(level[0]), float(level[1])
else:
min_v, max_v = 0.0, float(level)
else:
cur_amp = self._resolve_val(amplitude)
cur_bias = self._resolve_val(bias)
min_v, max_v = cur_bias, cur_bias + cur_amp
vals = []
while len(vals) < pts_total:
v = self._rng.uniform(min_v, max_v)
step = max(1, int(self._parse_to_ms(interval) // s_period))
vals.extend([v] * step)
return self._create_series(np.array(vals[:pts_total]), delay)
def generate_spike(self, gen_time=None, amplitude=1.0, bias=0.0, interval="1s", delay="0ms") -> pd.Series:
"""
間欠的なスパイク(突出値)を生成します。
Args:
amplitude (float): スパイクの高さ(biasからの加算値)。
bias (float): スパイクがない区間のベース値。
interval (str): スパイクが発生する間隔。
"""
s_period = self.default_sampling_period
g_time = self._parse_to_ms(gen_time) or self.default_gen_time
cur_bias = self._resolve_val(bias)
pts_total = int(g_time // s_period)
# ベースライン(bias)で埋める
vals = np.full(pts_total, float(cur_bias))
# スパイク生成ループ
i = 0
while i < pts_total:
# スパイク値を加算 (amplitudeは正負どちらも可)
vals[i] += self._resolve_val(amplitude)
# 次の間隔へ
step = max(1, int(self._parse_to_ms(interval) // s_period))
i += step
return self._create_series(vals, delay)
# =========================================================================
# Processing Methods (パラメータ統一版API)
# =========================================================================
def limit(self, series: pd.Series, upper: float = None, lower: float = None,
delay: str = "0ms", interval=None, duration=None, max_repeats=None, fill_after=None) -> pd.Series:
"""
波形をクリッピングします。
interval指定により「間欠的にサチレーションを起こすセンサー故障」なども表現可能です。
"""
# 演算ロジック: 単純なclip
operation = lambda s: s.clip(lower=lower, upper=upper)
return self._apply_operation(series, operation, delay, interval, duration, max_repeats, fill_after)
def multiply(self, series: pd.Series, factor: float,
delay: str = "0ms", interval=None, duration=None, max_repeats=None, fill_after=None) -> pd.Series:
"""
波形を増幅/減衰させます。
interval指定により「時々ゲインが跳ね上がる」挙動などが表現可能です。
"""
# 演算ロジック: 単純な掛け算
operation = lambda s: s * factor
return self._apply_operation(series, operation, delay, interval, duration, max_repeats, fill_after)
def decay(self, series: pd.Series, rate: float = 0.9,
delay: str = "0ms", interval=None, duration=None, max_repeats=None, fill_after=None) -> pd.Series:
"""
波形を減衰させます。
指定された期間(duration)の中で、開始から終了に向かって指数関数的に減衰します。
intervalを指定すると、衝撃波形のような「減衰の繰り返し」を表現できます。
"""
# 演算ロジック: 時間経過に応じた減衰係数を掛ける
def operation(s):
n = len(s)
steps = np.arange(n)
# ウィンドウの先頭を1.0として、1ステップごとにrate倍していく
factors = rate ** steps
return s * factors
return self._apply_operation(series, operation, delay, interval, duration, max_repeats, fill_after)
def trend(self, series: pd.Series, start: float = 0.0, end: float = 1.0,
delay: str = "0ms", interval=None, duration=None, max_repeats=None, fill_after=None) -> pd.Series:
"""
波形にトレンドを加算します。
intervalを指定すると「鋸歯状(のこぎり状)」にトレンドがリセットされて繰り返されます。
"""
# 演算ロジック: linspaceを加算
def operation(s):
n = len(s)
trend_vals = np.linspace(start, end, n)
return s + trend_vals
return self._apply_operation(series, operation, delay, interval, duration, max_repeats, fill_after)
# --- 管理・出力 ---
def merge(self, series_list: List[pd.Series]) -> pd.Series:
"""複数のSeriesを合成(加算)します"""
if not series_list: return pd.Series()
return sum(series_list)
def add(self, name: str, series: pd.Series):
self.signals[name] = series
def create_dataframe(self) -> pd.DataFrame:
if not self.signals: return pd.DataFrame()
return pd.DataFrame(self.signals).reset_index().rename(columns={"index":"timestamp"})
まとめ
データ分析では、さまざまなアルゴリズムを試したくても、「本物のデータが手に入らない」という壁にぶつかることが少なくありません。 そんなとき、それっぽいデータを自分で作れたら、事前に検証や準備ができて、開発のスピードもぐんと上がります。
SignalComposer を使えば、これまで手作業では再現が難しかった、
- 故障による速度低下や異常発熱などの物理現象の連鎖
- センサの計測限界による波形のクリップ現象
といった複雑なシナリオも、わずか数行のコードで簡単に再現できるようになります。
もしそれっぽいテストデータの必要が生じたら、是非この記事をご活用ください。


コメント