前回の記事では、鋭い異常変化(スパイク)を捉えるための「ウェーブレット変換」を使って、異常検知・時間周波数解析を行う方法を解説しました。

ウェーブレット変換は「突発的な異常」には最強ですが、現場の課題はそれだけではありません。 「サーッという持続的なノイズを消したい」「AIに学習させるためにデータを画像化したい」といったニーズには、信号処理の王道である STFT(短時間フーリエ変換) が圧倒的に便利です。
そこで今回は、ウェーブレット変換の「対」となる技術、STFTを解説します。 Pythonの SciPy ライブラリを使えば、わずか数行で「ノイズ除去、異常検知、時間周波数解析、AI前処理」の4つを実現できます。
STFT(短時間フーリエ変換)とは
STFT(Short-Time Fourier Transform)は、一言で言えば「『いつ』その音が鳴ったか」を知るための分析手法です。
通常、周波数解析といえば「FFT(高速フーリエ変換)」が有名ですが、FFTには「時間の情報が消えてしまう」という致命的な弱点があります。これを克服するために開発されたのがSTFTです。
FFTとSTFTの違い
FFT(高速フーリエ変換)を音楽に例えると、曲に使われている音程を一気にすべて洗い出す手法です。
この曲は、ド、ミ、ソの3音だけで構成されていることは分かりますが、時間的は変化は分かりません。
一方でSTFTは、曲の楽譜のようなもので、「最初の10秒はドの音、次の10秒はミの音」というように、「いつ(時間)」「どの高さの音(周波数)が」「どれくらいの強さで」鳴っているかをすべて可視化できます。
どうやって分析しているの?(スライディング処理のイメージ)
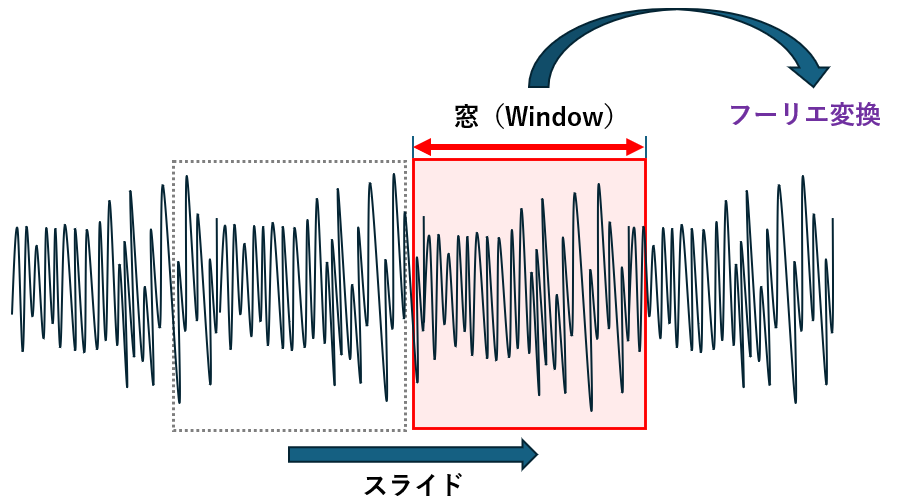
STFTの仕組みは非常にシンプルです。 長い信号を一度に分析するのではなく、「短い区間(窓)」に切り取って、少しずつ時間をずらしながらFFTを繰り返すのです。
- 信号の「最初のわずかな時間」だけを切り取る。
- その部分だけFFTにかける。
- 切り取る場所を少し右にずらす(スライドさせる)。
- またFFTにかける……。
これを最後まで繰り返すことで、パラパラ漫画のように時間の経過に伴う周波数の変化を記録することができます。この結果を並べて描画したものが、いわゆる「スペクトログラム(声紋)」です。
重要なパラメータの決め方は?(窓関数と窓幅)
STFTを行う際に重要となるのが window(窓関数)と nperseg(窓幅)の設定です。
窓関数の種類(Window Type)
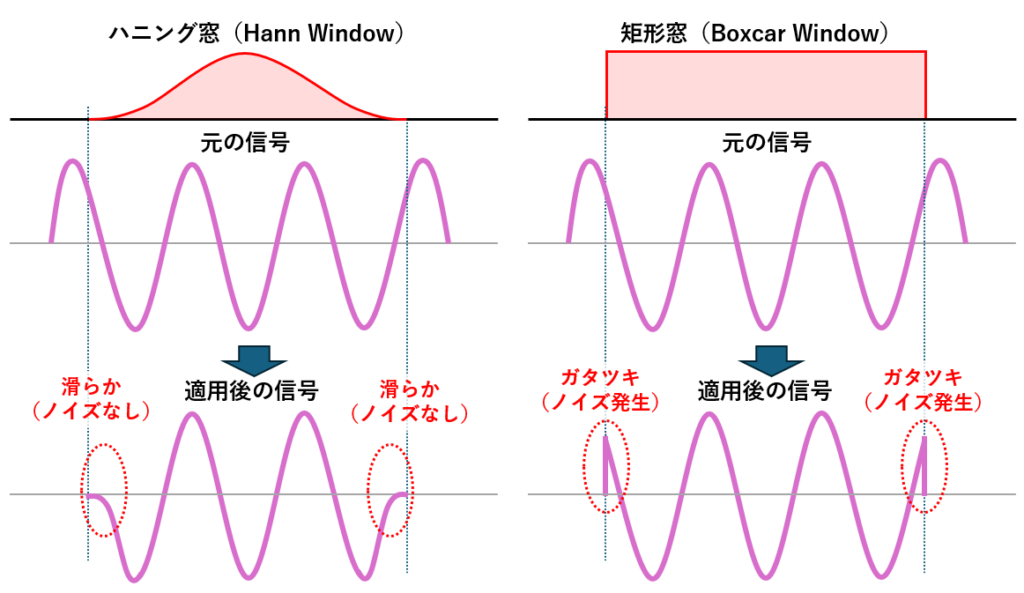
「窓」とは、長い信号データから分析したい部分を切り抜くための枠のようなものです。 しかし、何も考えずに長方形の枠で単純に切り取ってしまう(矩形窓)と、切り口で波形がブツリと途切れ、「崖(不連続点)」ができてしまいます。
FFTはこの「崖」を「急激な信号の変化」と勘違いしてしまうため、本来存在しないはずの周波数成分(ノイズ)が大量に発生してしまいます。これを「スペクトル漏れ」と呼びます。
このノイズを防ぐために、通常は「ハニング窓」を用います。 ハニング窓は、切り取る区間の両端を滑らかにゼロに押しつぶすことで、切り口の「崖」をなくし、きれいな分析結果を得ることができます。
- ハニング窓(hann)
最も一般的でバランスが良い。「切り取った両端」を滑らかにゼロにするため、不自然なノイズ(スペクトル漏れ)が出にくいのが特徴です。 - 矩形窓(boxcar)
何もしない(ただの長方形)。信号の端っこでノイズが大量に出るため、通常の分析ではあまり使いません。
窓幅(Window Width)
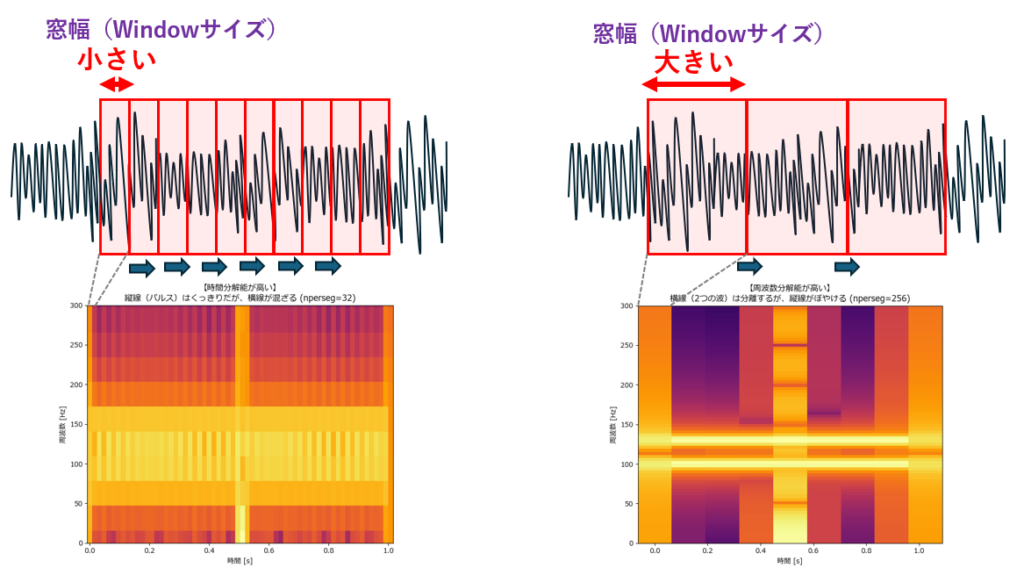
ここがSTFTの最重要ポイントです。nperseg(1つの窓に含まれるデータ点数)をどう設定するかで、分析結果は劇的に変わります。
ここには「不確定性原理」と呼ばれる、絶対に避けられないトレードオフが存在します。
左側:窓を小さく(短く)した場合
- 時間重視: 細かい区間で区切るため、縦の線(一瞬のパルス)がくっきり見え、「いつ鳴ったか」が正確に分かります。
- 弱点: その代わり、一度に見る波の長さが足りず、横の線(周波数)がボヤけて混ざってしまいます。
右側:窓を大きく(長く)した場合
- 周波数重視: 長い区間で波を見るため、横の線がくっきり分かれ、「音の高さの違い」が正確に分かります。
- 弱点: その代わり、時間の区切りが大雑把になり、縦の線(パルス)が横に伸びて「いつ鳴ったか」が曖昧になります。
何に使えるの?(メリット・デメリット)
「ウェーブレット変換があるなら、全部それでいいんじゃない?」と思うかもしれません。
しかし、STFTには「計算が速い」「元に戻しやすい」という圧倒的な強みがあり、今でも現場では「まずはSTFT」が定石です。
STFTのメリット
- 「元に戻せる」のが簡単(可逆性)
- これが最大の武器です。
signal.stftでバラバラにした後、不要な成分(ノイズ)を捨てて、signal.istftで元の波形に組み立て直すことができます。 - ウェーブレット変換でも逆変換は可能ですが、STFTの方が計算がシンプルで、音質を保ったまま復元するのが得意です。
- これが最大の武器です。
- 計算がとにかく速い
- 中身は高速な「FFT」の繰り返しなので、非常に高速です。リアルタイムの音声波形表示や、大量の振動データの処理に向いています。
- AI(ディープラーニング)との相性が抜群
- 解析結果(スペクトログラム)が綺麗な「画像」になるため、画像認識AI(CNN)の技術をそのまま転用できます。「異常音検知AI」を作る場合、「STFTで画像化してAIに学習させる」のが現在の王道パターンです。
STFTのデメリット
「あちらを立てればこちらが立たず」のジレンマ
- 先ほど解説した通り、窓の長さを一度決めたら、全体を通してその長さでしか分析できません。
- 「低周波はじっくり見たいけど、高周波の一瞬の変化も見逃したくない」という欲張りな要求には応えられません。(これを解決できるのが、窓の大きさを周波数によって変えられる「ウェーブレット変換」です)
結論:どう使い分ける?
- ノイズを除去したい / AIに食わせたい ⇒ STFT(今回の主役)
- いつ起きたか分からない「一瞬の異常」を見つけたい⇒ウェーブレット変換
このように、目的が「全体処理・加工」ならSTFT、「精密検査」ならウェーブレット変換、という使い分けがベストです。
STFTを使ったノイズ除去(スペクトルサブトラクション)
一言でいうと「ノイズの『指紋』を採取して、引き算する」手法です。
- ノイズ採取: データの中の「無音区間(信号がなくノイズだけの区間)」を分析し、「どんな周波数のノイズが、どれくらいの強さで鳴っているか(=ノイズの指紋)」を計算します。
- 引き算: 全体のデータから、その「ノイズの指紋」の分だけ成分を引き算します。
これにより、単純なカット(ゲート法)では消しきれない「信号の裏で鳴っているサーッというノイズ」まできれいに除去できます。
以下はノイズ除去のサンプルです。 「最初の0.1秒はノイズだけの区間である」と仮定して処理を行う関数になっています。
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
# 日本語フォント設定(環境に合わせて変更してください)
# Windowsなら 'Meiryo', Macなら 'Hiragino Sans' など
plt.rcParams['font.family'] = 'Meiryo'
def generate_test_data(duration=1.0, fs=1000, freq=50, noise_std=0.5, silence_duration=0.1):
"""
テストデータ生成関数
スペクトルサブトラクション用に、冒頭に「無音(ノイズのみ)」区間を作ります。
Parameters
----------
duration : float
データの長さ(秒)。
fs : int
サンプリング周波数 (Hz)。
freq : float
生成するサイン波の周波数 (Hz)。
noise_std : float
ノイズの強さ(標準偏差)。
silence_duration : float
冒頭の「信号なし・ノイズのみ」の区間の長さ(秒)。
ここでノイズの性質を学習させるため、必ず設定します。
Returns
-------
t : ndarray
時間軸データ。
clean : ndarray
正解データ(ノイズなし)。
data : ndarray
入力データ(正解 + ノイズ)。
"""
t = np.linspace(0, duration, int(fs * duration))
# 正解データ(信号)
clean = np.sin(2 * np.pi * freq * t)
# ★重要:最初の silence_duration 秒は信号をゼロにする(ノイズ学習用)
silence_points = int(fs * silence_duration)
clean[:silence_points] = 0
# ノイズ
np.random.seed(42)
noise = np.random.normal(0, noise_std, len(t))
# 入力データ(正解 + ノイズ)
data = clean + noise
return t, clean, data
def spectral_subtraction(data, fs, noise_end_time=0.1, nperseg=256, alpha=1.0):
"""
スペクトルサブトラクション法によるノイズ除去関数
Parameters
----------
data : array_like
入力信号データ(1次元配列)。
fs : int
サンプリング周波数 (Hz)。
noise_end_time : float
ノイズ「だけ」が鳴っているとみなす最初の期間(秒)。
ここから「ノイズの指紋(周波数特性)」を学習します。
nperseg : int
STFTの窓幅。デフォルトは256。
alpha : float
引き算の強さ(係数)。デフォルトは1.0。
ノイズが消えにくい場合は 1.5 や 2.0 に上げますが、
上げすぎると「ミュージカルノイズ(シャリシャリ音)」が発生しやすくなります。
Returns
-------
cleaned_signal : ndarray
ノイズ除去後の信号データ。
"""
# 1. STFTで周波数領域へ
f, t_stft, Zxx = signal.stft(data, fs, window='hann', nperseg=nperseg)
# 2. ノイズの指紋(プロファイル)を作成
# 時間軸 t_stft から、ノイズ学習区間(最初の noise_end_time 秒)のインデックスを探す
noise_idx = np.where(t_stft <= noise_end_time)[0]
# その区間の振幅スペクトルの平均をとる
if len(noise_idx) == 0:
# 万が一、区間短すぎてインデックスが取れなかった場合の安全策
noise_profile = np.zeros((Zxx.shape[0], 1))
else:
noise_profile = np.mean(np.abs(Zxx[:, noise_idx]), axis=1, keepdims=True)
# 3. スペクトルサブトラクション(引き算)
amp = np.abs(Zxx) # 全体の振幅
phase = np.angle(Zxx) # 全体の位相
# ノイズプロファイルを引き算(マイナスになったら0にする)
# alpha倍して引くことで、少し強めにノイズを抑制できます
amp_cleaned = np.maximum(amp - (alpha * noise_profile), 0)
# 4. ISTFTで波形に戻す
# 修正した振幅と、元の位相を組み合わせて復元
Zxx_cleaned = amp_cleaned * np.exp(1j * phase)
_, cleaned_signal = signal.istft(Zxx_cleaned, fs)
# ★重要修正:元のデータ長さに合わせる(エラー回避)
# ISTFTの結果はパディングで少し長くなることがあるため、元の長さに切り揃えます
return cleaned_signal[:len(data)]
def plot_results(t, clean, noisy, denoised):
"""
結果比較プロット関数(3段構成)
Parameters
----------
t : ndarray
時間軸。
clean : ndarray
正解データ。
noisy : ndarray
入力データ(ノイズあり)。
denoised : ndarray
除去後データ。
"""
plt.figure(figsize=(10, 8)) # 縦長に見やすく調整
# --- 1段目:正解データ ---
plt.subplot(3, 1, 1)
plt.plot(t, clean, color='red', linestyle='-', label='正解データ')
plt.title("正解データ(本来の信号)")
plt.ylabel("振幅")
plt.grid(True, alpha=0.3)
plt.legend(loc='upper right')
# --- 2段目:正解データにノイズを加算 ---
plt.subplot(3, 1, 2)
plt.plot(t, noisy, color='gray', alpha=0.8, label='入力データ')
plt.title("正解データにノイズを加算")
plt.ylabel("振幅")
plt.grid(True, alpha=0.3)
plt.legend(loc='upper right')
# --- 3段目:ノイズ除去結果 ---
plt.subplot(3, 1, 3)
plt.plot(t, denoised, color='blue', label='除去後データ')
plt.title("ノイズ除去結果(スペクトルサブトラクション後)")
plt.xlabel("時間 [s]")
plt.ylabel("振幅")
plt.grid(True, alpha=0.3)
plt.legend(loc='upper right')
plt.tight_layout()
plt.show()
if __name__ == "__main__":
# パラメータ設定
FS = 1000 # サンプリング周波数
NOISE_LEARN_SEC = 0.1 # ノイズ学習に使う冒頭の時間(秒)
# 1. データの準備
# 冒頭0.1秒は「ノイズのみ」の区間として生成します
t, clean_sig, noisy_sig = generate_test_data(fs=FS, silence_duration=NOISE_LEARN_SEC)
# 2. ノイズ除去の実行
# alpha=2.0 で標準よりも強めにノイズを除去します
denoised_sig = spectral_subtraction(noisy_sig, FS, noise_end_time=NOISE_LEARN_SEC, alpha=2.0)
# 3. 結果の描画
plot_results(t, clean_sig, noisy_sig, denoised_sig)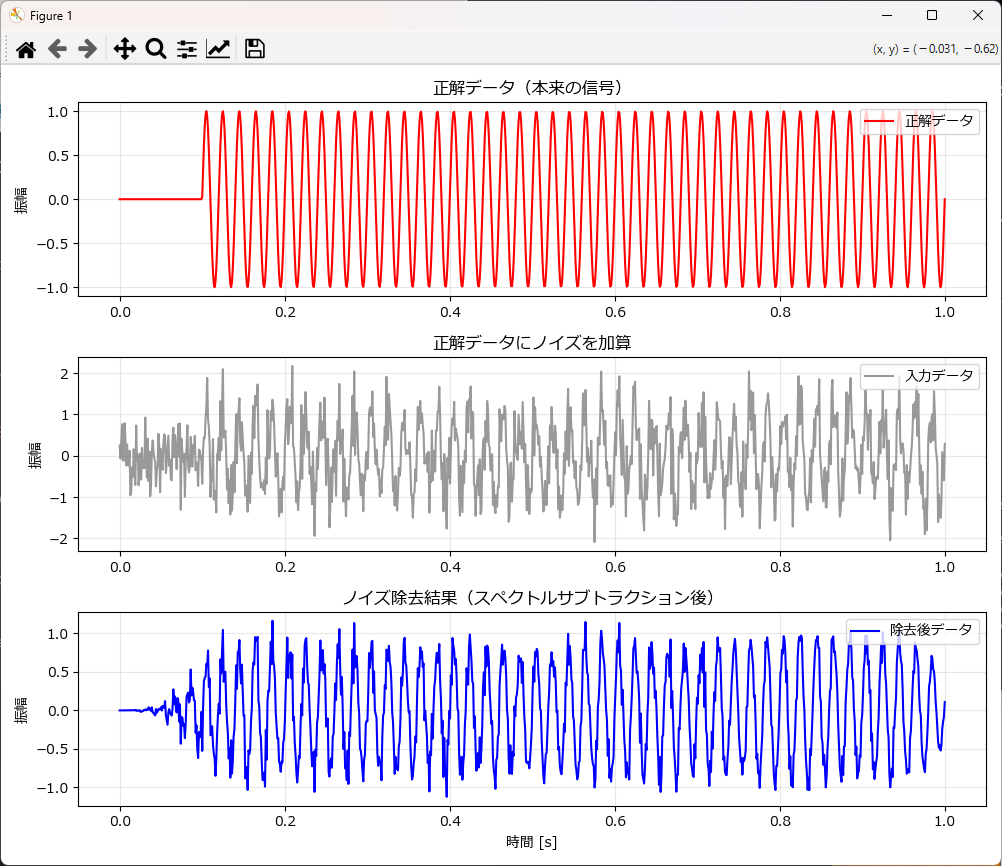
STFTを使った異常検知
STFTを使った異常検知は、「特定の周波数帯(バンド)のエネルギー監視」 という手法が最も一般的で強力です。
単に波形の振幅(音の大きさ)を見るだけでは、「低いゴォーという動作音(正常)」に埋もれて、「キーッという金属音(異常)」が検知できません。 しかしSTFTを使えば、「動作音は無視して、金属音の周波数帯だけを監視する」 ことができるため、感度が劇的に向上します。
異常検知の手順
やり方は非常にシンプルで、以下の4ステップです。
- STFT変換
signal.stft を使い、波形データを「時間×周波数」の強度データ(スペクトログラム)に変換します。 - バンド抽出
全周波数を見るのではなく、異常が発生するであろう「特定の周波数帯(今回は200Hz〜400Hz)」だけをピンポイントで切り出します。 - エネルギー計算(スコア化)
切り出した帯域の強さを時間ごとに合計し、「異常スコア(band_energy)」 という1本の時系列データに圧縮します。 - 3シグマ判定(自動検知)
最初の数秒(正常区間)から「平均と標準偏差(シグマ)」を計算し、統計的に閾値を自動設定します。スコアがこのライン(平均 +3σ)を超えた瞬間を「異常発生」とみなします。
この手法を使えば、「見た目の波形は全然変わっていないのに、異常だけを即座に検知する」 ことが可能です。
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
# 日本語フォント設定
plt.rcParams['font.family'] = 'Meiryo'
def generate_anomaly_data(duration=2.0, fs=1000):
"""
テストデータ生成:正常な低い揺れの中に、一瞬だけ高い異常振動を混ぜる
"""
t = np.linspace(0, duration, int(fs * duration))
# 1. 正常信号(50Hzの低い揺れ)
normal_sig = np.sin(2 * np.pi * 50 * t) * 0.5
# 2. 異常信号(300Hzの高い揺れ):1.0秒〜1.2秒の間だけ発生
anomaly_sig = np.zeros_like(t)
anomaly_period = (t >= 1.0) & (t <= 1.2)
anomaly_sig[anomaly_period] = np.sin(2 * np.pi * 300 * t[anomaly_period]) * 0.3
# 3. ノイズ(全体にうっすら)
np.random.seed(42)
noise = np.random.normal(0, 0.2, len(t))
# 合成
data = normal_sig + anomaly_sig + noise
return t, data
def stft_anomaly_detection(data, fs, target_band=(200, 400), threshold=3.0, nperseg=64):
"""
STFTを使った特定周波数バンド監視による異常検知
Parameters:
target_band : tuple
監視したい周波数範囲 (min_hz, max_hz)
ここでは「異常音」が鳴るであろう 200Hz〜400Hz を監視します。
threshold : float
異常とみなすエネルギーの閾値
Returns:
t_stft : time axis
band_energy : 計算された「異常スコア」の時系列
anomaly_detected : 閾値を超えたかどうかの判定フラグ配列
"""
# 1. STFT実行
f, t_stft, Zxx = signal.stft(data, fs, window='hann', nperseg=nperseg)
magnitude = np.abs(Zxx)
# 2. 監視バンドの抽出
min_f, max_f = target_band
# 周波数軸 f の中から、ターゲット範囲内のインデックスを探す
target_idx = np.where((f >= min_f) & (f <= max_f))[0]
# 3. バンドエネルギー(異常スコア)の計算
# 抽出した周波数帯の振幅を合計(または平均)する
# axis=0 は周波数方向への合計 = 「その時間の、その帯域の総エネルギー」
band_energy = np.sum(magnitude[target_idx, :], axis=0)
# 4. 閾値判定
anomaly_detected = band_energy > threshold
return t_stft, band_energy, anomaly_detected, f, magnitude
def plot_anomaly_results(t, data, t_stft, band_energy, threshold, f, magnitude):
"""
結果を描画する関数
"""
plt.figure(figsize=(10, 8))
# --- 1段目:元の波形 ---
plt.subplot(3, 1, 1)
plt.plot(t, data, color='gray', label='観測波形')
plt.title("1. 元の波形(低い揺れに埋もれて、異常が見えにくい)")
plt.ylabel("振幅")
plt.grid(True, alpha=0.3)
# 異常発生区間を赤枠で囲む目安
plt.axvspan(1.0, 1.2, color='red', alpha=0.1, label='実際の異常区間')
plt.legend(loc='upper right')
# --- 2段目:スペクトログラム ---
plt.subplot(3, 1, 2)
plt.pcolormesh(t_stft, f, np.abs(magnitude), shading='gouraud', cmap='inferno')
plt.title("2. STFTスペクトログラム(300Hz付近に反応あり)")
plt.ylabel("周波数 [Hz]")
# 監視エリアを点線で示す
plt.axhline(200, color='white', linestyle='--')
plt.axhline(400, color='white', linestyle='--', label='監視バンド')
plt.legend(loc='upper right')
# --- 3段目:異常スコア(バンドエネルギー) ---
plt.subplot(3, 1, 3)
plt.plot(t_stft, band_energy, color='blue', linewidth=2, label='異常スコア(特定バンドの強さ)')
plt.axhline(threshold, color='red', linestyle='-', linewidth=2, label=f'閾値 ({threshold})')
# 閾値を超えた部分を塗りつぶす
plt.fill_between(t_stft, band_energy, threshold, where=(band_energy > threshold),
color='red', alpha=0.5, interpolate=True)
plt.title("3. 異常検知結果(監視バンド内のエネルギー推移)")
plt.xlabel("時間 [s]")
plt.ylabel("スコア")
plt.grid(True, alpha=0.3)
plt.legend(loc='upper right')
plt.tight_layout()
plt.show()
if __name__ == "__main__":
# パラメータ設定
FS = 1000
# 1. データ生成(1.0〜1.2秒に異常発生)
t, data = generate_anomaly_data(duration=2.0, fs=FS)
# 2. まず異常検知関数を呼び出して、スコア(band_energy)を取得する
# ※この時点では閾値は何でも良いので適当に 0 を入れておく
t_stft, score, _, f, mag = stft_anomaly_detection(
data, FS,
target_band=(200, 400),
threshold=0,
nperseg=64
)
# -------------------------------------------------------
# ★ここが3シグマ法の追加実装部分
# -------------------------------------------------------
# 最初の0.5秒間を「正常な学習期間」とする
learn_idx = np.where(t_stft < 0.5)[0]
# 正常期間のスコアだけを取り出す
normal_scores = score[learn_idx]
# 平均と標準偏差を計算
mean_val = np.mean(normal_scores)
std_val = np.std(normal_scores)
# 3シグマで閾値を自動決定
dynamic_threshold = mean_val + 3 * std_val
print(f"学習した平均: {mean_val:.3f}")
print(f"学習した標準偏差: {std_val:.3f}")
print(f"自動決定された閾値 (3シグマ): {dynamic_threshold:.3f}")
# -------------------------------------------------------
# 3. 決定した閾値を使って、再度判定&描画を行う
# (再計算せずとも描画関数に渡すだけでOK)
plot_anomaly_results(t, data, t_stft, score, dynamic_threshold, f, mag)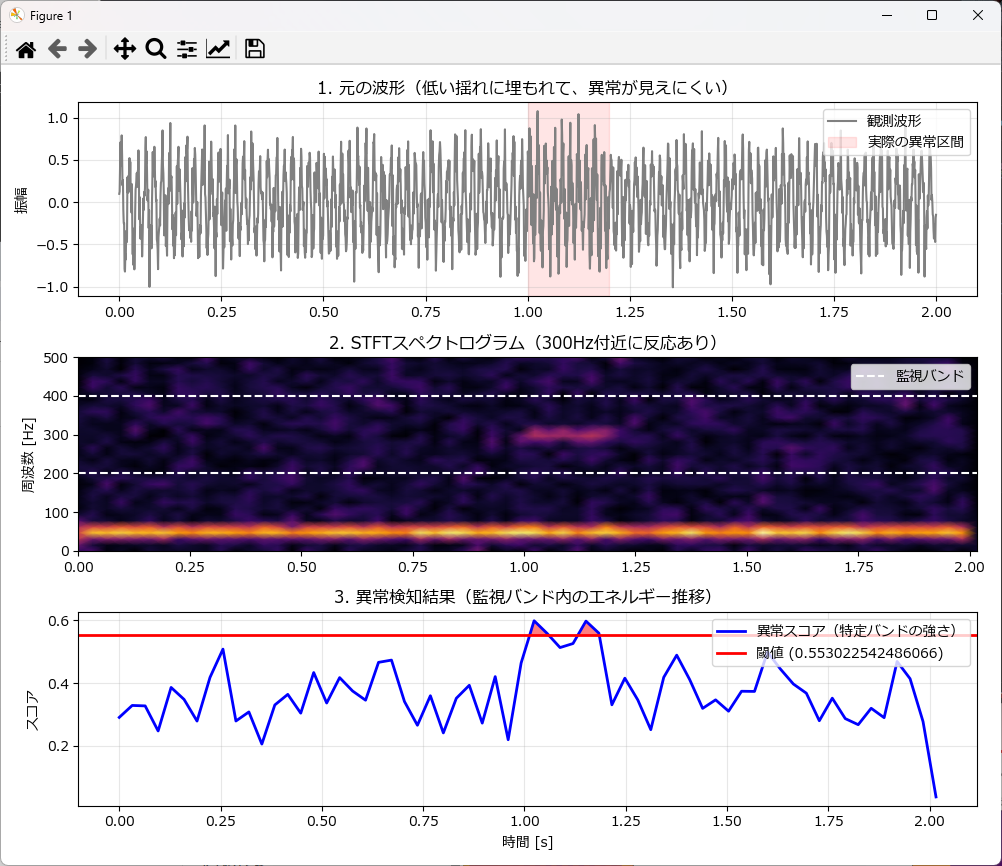
ここで、グラフ中央の「スペクトログラム」について少し解説します。
- 横軸:時間
- 縦軸:音の高さ(下のほうが低い音、上のほうが高い音)
- 色:音の強さ(黄色く光っているほど「音が大きい」、暗い紫色は「音が小さい(または無音)」)
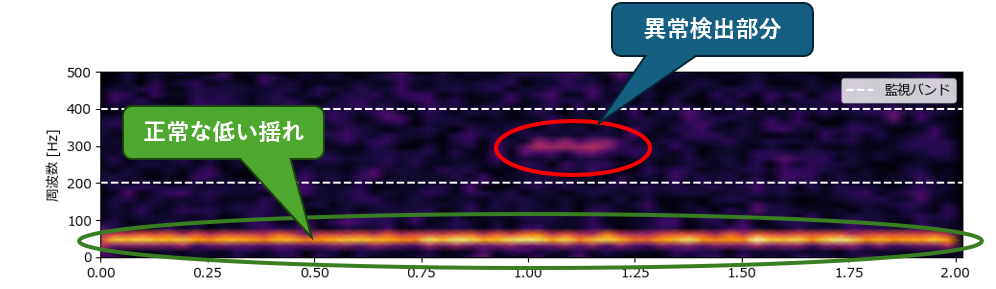
一番下(50Hz付近)に、最初から最後までずっと光っている太い黄色の線がありますが、 これはテストデータの「正常な低い揺れ(normal_sig)」です。 機械が動いている間はずっと鳴っている音なので、異常ではありません。
点線で囲まれた「監視バンド(200Hz〜400Hz)」の中を見ると、普段は真っ暗(何もない)はずの場所に、1.0秒のところだけ、ポツンと明るいモヤが出ていますが、これが、テストデータに含まれる「300Hzの異常振動(anomaly_sig)」です。
「普段は静かなエリアに、急に侵入者が現れた」ような状態なので、これをプログラムが検知したのです。
もし「波形の大きさ」だけで判断しようとすると、下の「太い黄色の線(正常音)」のエネルギーが強すぎるため、上の「小さなモヤ(異常音)」は埋もれて気づけません。
しかし、こうして周波数で分ける(STFTする)ことで、「うるさい正常音(下)」と「小さな異常音(上)」を切り離して見ることができるため、この小さな赤い丸の部分だけをピンポイントで見つけ出せます。
STFTを使った時間周波数解析(スペクトログラム)
時間周波数解析(スペクトログラム)は、STFTの最も基本かつ重要な機能です。 単に「周波数を分析する」だけでなく、「音の高さが時間とともにどう移り変わっていくか」を可視化します。
FFT(高速フーリエ変換)弱点は、「いつ」その音が鳴ったかが分からないことでした。 STFTを使ってそれを解決し、「時間・周波数・強さ」の3次元情報を、2次元の地図(ヒートマップ)として描いたものを「スペクトログラム」と呼びます。
- 横軸: 時間(いつ?)
- 縦軸: 周波数(どの高さの音が?)
- 色: 強さ(どれくらいの音量で?)
これを使うことで、エンジンの回転数が上がっていく様子や、小鳥のさえずりのような複雑な音の変化を「見て」理解できるようになります。
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
# 日本語フォント設定
plt.rcParams['font.family'] = 'Meiryo'
def plot_spectrogram(data, fs, nperseg=256, window='hann', title="スペクトログラム解析"):
"""
STFTを行い、スペクトログラム(時間周波数マップ)を描画する関数
Parameters
----------
data : array_like
解析したい1次元の波形データ(時系列データ)。
fs : int
サンプリング周波数 (Hz)。
1秒間に何個のデータがあるか(例: 1000, 44100など)。
nperseg : int, optional
窓幅(1つの窓に含まれるデータ点数)。デフォルトは256。
この値を大きくすると「周波数」が細かく見え、小さくすると「時間」が細かく見えます。
(2の乗数推奨: 64, 128, 256, 512...)
window : str, optional
窓関数の種類。デフォルトは 'hann' (ハニング窓)。
通常はこのままでOKですが、用途に応じて 'boxcar' (矩形窓) や 'hamming' (ハミング窓) も指定可能。
title : str, optional
グラフのタイトル。
"""
# 1. STFT実行
f, t_stft, Zxx = signal.stft(data, fs, window=window, nperseg=nperseg)
# 2. 強度(振幅)をデシベル(dB)に変換
# そのままだと値の差が大きすぎて見づらいため、対数変換するのが定石です
magnitude = np.abs(Zxx)
log_magnitude = 20 * np.log10(magnitude + 1e-10) # 1e-10はlog(0)エラー回避用
# 3. 描画
plt.figure(figsize=(10, 6))
# pcolormeshでヒートマップを描く
# shading='gouraud' にすると、カクカクせず滑らかに表示されます
plt.pcolormesh(t_stft, f, log_magnitude, shading='gouraud', cmap='inferno')
plt.title(title)
plt.ylabel('周波数 [Hz]')
plt.xlabel('時間 [s]')
# カラーバー(右側の目盛り)
cbar = plt.colorbar()
cbar.set_label('強度 [dB]')
plt.tight_layout()
plt.show()
# ==========================================
# テストデータの生成と実行
# ==========================================
def generate_chirp_data(duration=2.0, fs=1000):
"""
テストデータ生成:
1. チャープ信号(周波数が低いところから高いところへ移動する)
2. インパルスノイズ(一瞬の衝撃)
"""
t = np.linspace(0, duration, int(fs * duration))
# 1. チャープ信号 (0秒で50Hz → 2秒で300Hz までリニアに上昇)
chirp_sig = signal.chirp(t, f0=50, t1=duration, f1=300, method='linear')
# 2. バーストノイズ(1.0秒付近で一瞬だけ「ブチッ」と入る広帯域ノイズ)
burst_sig = np.zeros_like(t)
burst_sig[int(fs*1.0):int(fs*1.05)] = np.random.normal(0, 1.0, int(fs*0.05))
return t, chirp_sig + burst_sig
if __name__ == "__main__":
# パラメータ設定
FS = 1000
# 1. データ生成
t, data = generate_chirp_data(duration=2.0, fs=FS)
# 2. 元波形の確認
plt.figure(figsize=(10, 3))
plt.plot(t, data, color='gray', linewidth=0.8)
plt.title("元の波形(周波数の変化は目で見て分からない)")
plt.xlabel("時間 [s]")
plt.tight_layout()
plt.show()
# 3. スペクトログラム解析の実行
plot_spectrogram(data, FS, nperseg=128, title="【解析結果】STFTスペクトログラム")プログラムを実行すると、以下の2つのグラフが表示されます。
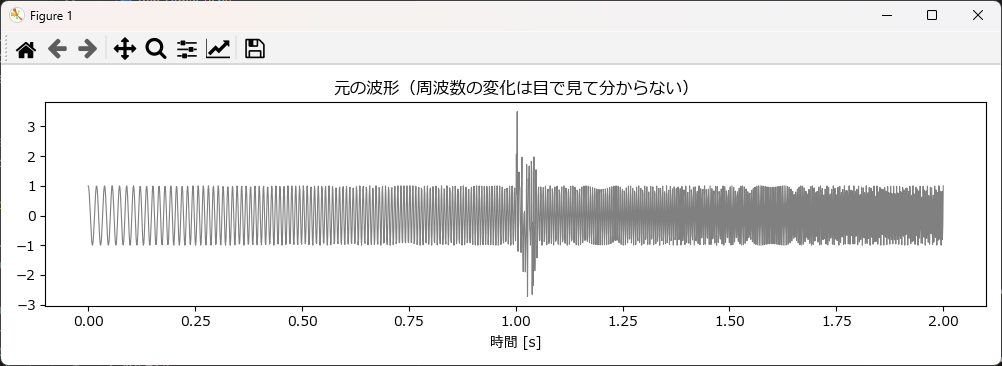
まず1つ目は、「元の波形(時間軸データ)」をそのままプロットしたものです。
ご覧の通り、パッと見ではただの「塗りつぶされた帯」や「ノイズ」にしか見えません。 実はこの中に「徐々に音程が上がる信号(チャープ)」が含まれているのですが、波形の形を見ただけでは、周波数の変化を目視で確認することは非常に困難です。
2つ目のグラフはスペクトログラムです。1つ目の波形グラフでは「ただのノイズの塊」に見えていたデータが、STFTを通すと「どのような音が鳴っているか」が手に取るように分かるようになります。
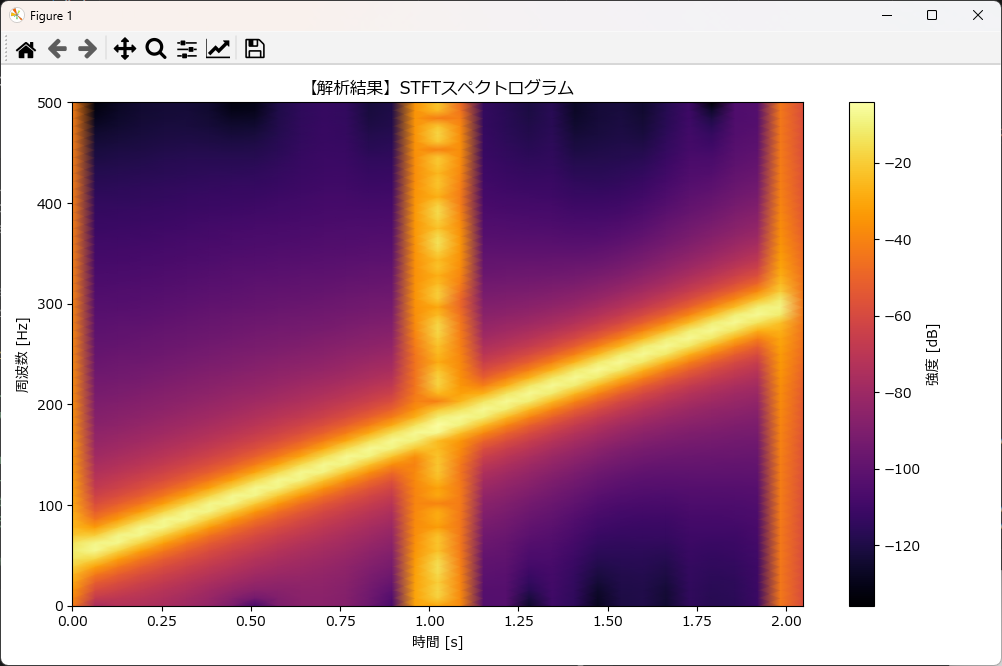
1. 右上がりの黄色い線(チャープ信号)
- 何が見える?: 左下から右上に向かって、一直線に伸びる明るい線があります。
- どういう意味?: これは「時間が経つにつれて、音程(周波数)が徐々に上がっている」ことを表しています。
- 0秒のときは低い音(約50Hz)
- 2秒のときは高い音(約300Hz)
- これがコードで生成した「キュイーン」というチャープ音の正体です。
2. 真ん中の太い縦線(バーストノイズ)
- 何が見える?: 1.0秒の地点に、下から上まで突き抜けるようなオレンジ色の柱が立っています。
- どういう意味?: これは「一瞬だけ鳴った『ブチッ』という衝撃音」です。
- 衝撃音(インパルス)は、「低い音から高い音まで、あらゆる周波数を同時に含む」という性質があります。そのため、特定の高さだけでなく、縦に長い線として現れるのです。
1つ目のグラフ(元の波形)では、この2つの音(チャープ音と衝撃音)が混ざり合って区別がつきませんでした。 しかし、スペクトログラムで見れば「普段はずっと音程が上がっているけど、1.0秒の時だけ突発的なノイズが入ったんだな」というストーリーが一目瞭然になります。
AI前処理
最近のAI開発、特に異常検知や音響分類の現場では、「音(1次元データ)をSTFTで画像(2次元データ)に変換し、画像認識AI(CNN)で学習させる」という手法がデファクトスタンダードになっています。
なぜわざわざ画像にするのでしょうか? それは、「画像認識の技術(ResNetやYOLOなど)の方が、音声処理技術よりも圧倒的に進化していて使いやすいから」です。
AI学習用の前処理ステップ
AIに学習させるためには、単にスペクトログラムを作るだけでなく、データの値を 0.0〜1.0 の範囲に収める「正規化(Normalization)」 が必須です。
- STFT変換: 時間×周波数のマップを作る。
- デシベル変換: 人間の聴覚やAIの特徴量に合わせるため対数変換する。
- 正規化 (Min-Max Scaling): データの最小値を0、最大値を1にする。
- 画像化: グレースケール(またはカラー)画像として保存する。
下記はAI学習用の画像を作成するサンプルプログラムです。この関数は、生の波形データを受け取り、AI(CNNなど)にそのまま入力できる「0〜1に正規化された2次元配列」と「保存用の画像ファイル」を出力します。
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
import os
# 日本語フォント設定
plt.rcParams['font.family'] = 'Meiryo'
def generate_chirp_data(duration=2.0, fs=1000, f_start=50, f_end=300):
"""
テストデータ生成関数:チャープ信号
時間が経つにつれて周波数がリニアに上がっていく信号を生成します。
AIの学習データとしてよく使われる「特徴的な形状」を持つ波形です。
Parameters
----------
duration : float
データの長さ(秒)。
fs : int
サンプリング周波数 (Hz)。
f_start : float
開始周波数 (Hz)。
f_end : float
終了周波数 (Hz)。
Returns
-------
t : ndarray
時間軸データ。
data : ndarray
生成された波形データ。
"""
t = np.linspace(0, duration, int(fs * duration))
# チャープ信号生成 (0秒でf_start → duration秒でf_end まで変化)
data = signal.chirp(t, f0=f_start, t1=duration, f1=f_end, method='linear')
return t, data
def preprocess_for_ai(data, fs, output_file="spectrogram.png", nperseg=256):
"""
音響データをAI(CNN)学習用に前処理する関数
STFTを行い、デシベル変換し、0.0〜1.0に正規化して画像として保存します。
Parameters
----------
data : ndarray
入力波形データ(1次元)。
fs : int
サンプリング周波数。
output_file : str
保存する画像ファイル名。
nperseg : int
STFTの窓幅。デフォルトは256。
Returns
-------
normalized_spec : ndarray
0.0〜1.0に正規化された2次元配列(AIモデルへの入力データとして使用可能)。
"""
# 1. STFTで周波数領域へ
f, t_stft, Zxx = signal.stft(data, fs, window='hann', nperseg=nperseg)
# 2. 強度(振幅)をデシベル(dB)に変換
magnitude = np.abs(Zxx)
# log0を防ぐために微小な値(1e-10)を足して対数変換
log_spec = 20 * np.log10(magnitude + 1e-10)
# 3. AI用に正規化 (Min-Max Scaling)
# 全体を 0.0 〜 1.0 の範囲に収めるのがAI学習の鉄則です
min_val = np.min(log_spec)
max_val = np.max(log_spec)
# ゼロ除算回避(真っ平らなデータが来た場合など)
if max_val - min_val == 0:
normalized_spec = np.zeros_like(log_spec)
else:
normalized_spec = (log_spec - min_val) / (max_val - min_val)
# --- ここから保存用処理 ---
# 4. 画像ファイルとして保存
# 軸や余白を消して、データ部分だけの画像を作ります
plt.figure(figsize=(4, 4)) # 正方形(224x224などのリサイズ前段階として扱いやすい)
plt.axes([0, 0, 1, 1]) # 余白を完全になくす
plt.axis('off') # 軸の目盛りを消す
# グレースケールで描画
plt.pcolormesh(t_stft, f, normalized_spec, shading='gouraud', cmap='gray')
plt.savefig(output_file, dpi=100, bbox_inches='tight', pad_inches=0)
plt.close() # メモリ解放
print(f"画像保存完了: {output_file}")
return normalized_spec
# ==========================================
# 実行サンプル
# ==========================================
if __name__ == "__main__":
# パラメータ設定
FS = 1000
DURATION = 2.0
# 1. テストデータ生成
t, wave_data = generate_chirp_data(duration=DURATION, fs=FS, f_start=50, f_end=300)
# 2. AI用前処理の実行
# カレントディレクトリに 'ai_input_sample.png' が生成されます
ai_input_data = preprocess_for_ai(wave_data, FS, output_file="ai_input_sample.png")
# 3. 結果確認(数値データのチェック)
print("-" * 30)
print("AI入力用データ確認")
print(f"データの形状 (Height, Width): {ai_input_data.shape}")
print(f"最大値 (Should be 1.0): {np.max(ai_input_data):.2f}")
print(f"最小値 (Should be 0.0): {np.min(ai_input_data):.2f}")
print("-" * 30)プログラムを実行すると、下記の内容がプロンプトに表示されます。
画像保存完了: ai_input_sample.png
AI入力用データ確認
データの形状 (Height, Width): (129, 17)
最大値 (Should be 1.0): 1.00
最小値 (Should be 0.0): 0.00
生成される画像は以下の通りです。これをAIに学習させます。

まとめ
本記事では、信号処理の強力な武器である STFT(短時間フーリエ変換) について、その仕組みからPythonによる実践的な実装までを解説しました。
今回紹介した4つのテクニックは、どれも現場ですぐに使えるものです。
- 時間周波数解析(スペクトログラム)
- 「いつ、どんな音が鳴ったか」を地図のように可視化する。
- ノイズ除去(スペクトルサブトラクション)
- 目的の信号を守りながら、背景ノイズだけをきれいに引き算する。
- 異常検知(バンド監視 + 3シグマ法)
- 波形の見た目には表れない「特定の周波数の異常」を、統計的に検知する。
- AI前処理(画像化 + 正規化)
- 音データを「画像」に変換し、強力な画像認識AI(CNN)に入力できる形にする。
前回の記事で紹介した「ウェーブレット変換」と今回の「STFT」。どちらを使うか迷ったときは、以下のように判断してみてください。
| STFTがおすすめ | ウェーブレット変換がおすすめ |
|---|---|
| 全体的な傾向を見たい時(エンジンの回転数上昇など) 「サーッ」という持続的なノイズを消したいとき AI(ディープラーニング)の前処理として画像を生成したいとき | 「コツン」という一瞬の衝撃や、不連続な変化を逃さず捉えたいとき |







コメント