「STFT」や「ウェーブレット変換」は、「いつ、どんな変化が起きたか」という時間ごとの推移を捉えるには最強のツールです。
しかし、現場のデータ分析では、必ずしも「いつ」の情報が必要なケースばかりではありません。 むしろ、「データ全体に潜む周期性を知りたい」「サーッという高周波ノイズを一括で消し去りたい」「AI(LightGBMなど)に入れるためのシンプルな数値特徴量が欲しい」といったニーズの方が頻繁に発生します。
そんな時、計算コストが重く、結果が画像(2次元)になってしまうSTFTを使うのはオーバースペックです。ここで輝くのが、信号処理の原点にして頂点である FFT(高速フーリエ変換) です。
今回は、信号処理の基本であるFFTを再評価します。 Pythonの NumPy や SciPy ライブラリを使えば、わずか数行のコードで「スペクトル解析、ノイズ除去(フィルタリング)、定常的な異常検知、AI特徴量抽出」の4つを実現できます。
FFT(高速フーリエ変換)とは
FFT(Fast Fourier Transform)は、一言で言えばデータの中に「『何(どの成分)』が含まれているか」を突き止めるための最強の分析手法です。 よく比較される「STFT(短時間フーリエ変換)」は時間を細かく区切って分析しますが、FFTはデータ全体を一気に計算します。「いつ」という時間情報は失われますが、その代わりにあらゆる周波数成分の「総量」や「存在」を、圧倒的な計算速度と精度で特定できます。
FFTとSTFTの違い
音楽に例えると、両者の違いは「楽譜」と「成分表」の違いに似ています。
- STFT(楽譜): 「最初の10秒はド、次の10秒はミ」というように、時間の流れに沿った変化が分かります。ストーリーを知りたい場合に適しています。
- FFT(成分表): 「この曲全体では、ドが50回、ミが30回、ソが20回使われている」という集計結果を一瞬で出します。「曲のストーリー(時間変化)」は分かりませんが、「調律が狂った音が混ざっていないか?(異常検知)」や「ベース音が強すぎるのでは?(ノイズ特定)」といった全体的な傾向や問題点を見抜くには、FFTの方が圧倒的にシンプルで強力です。
ご提示いただいたSTFT(スライディング処理)の解説を、FFT(一括処理・成分分解)のメカニズムと注意点に焦点を当てて書き換えました。
FFTでは「時間をずらす」工程がなくなる代わりに、「波形の重ね合わせ(成分分解)」という概念が中心になります。また、窓関数の説明は「切り出したデータの端っこ」の問題として再定義します。
どうやって分析しているの?(成分分解のイメージ)
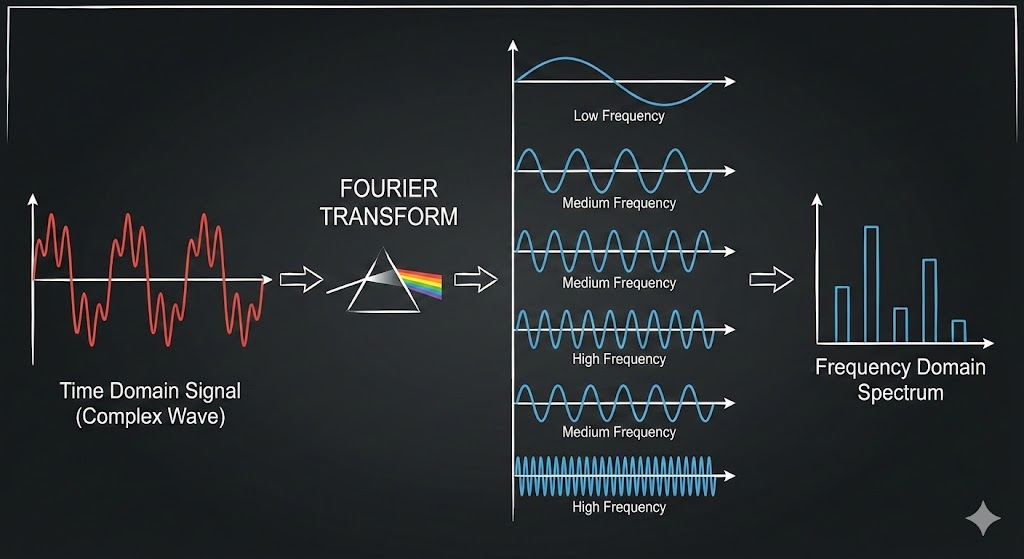
FFTの仕組みは、「プリズム」に例えられます。 太陽の光(白色光)をプリズムに通すと、虹色(赤・緑・青…)に分かれるように、FFTは複雑に入り混じった信号データを、「構成成分(周波数ごとのサイン波)」へと一瞬で分解します。
その原理は非常にシンプルで、以下の前提に基づいています。 「どんなに複雑な形の波形でも、実はたくさんの単純な波(サイン波)を足し合わせただけで表現できる」
- 分析したい信号データ全体を用意する。
- FFTにかける(数学的なフィルターを通す)。
- 「50Hzの波がこのくらい、120Hzの波がこのくらい…」という「成分表(スペクトル)」が出力される。
STFTのように時間をずらして何度も計算するのではなく、対象データを一発で計算するため、圧倒的に処理が高速なのが特徴です。
重要なパラメータの決め方は?(データ点数と窓関数)
FFTを行う際に重要となるのが、N(データ点数)とWindow(窓関数)の設定です。
窓関数の役割(なぜ必要なのか?)
FFTには「切り取ったデータが、永遠に繰り返されていると仮定して計算する」という特性があります。
しかし、現実のデータを適当な長さ(矩形窓)でブツリと切り取ると、データの「始点」と「終点」の高さがズレてしまい、繰り返したつなぎ目に「崖(不連続点)」ができてしまいます。 FFTはこの「崖」を「ものすごい急激な信号変化」と勘違いしてしまい、本来存在しないはずの周波数成分(ノイズ)を大量に発生させてしまいます。これを「スペクトル漏れ(リーク誤差)」と呼びます。
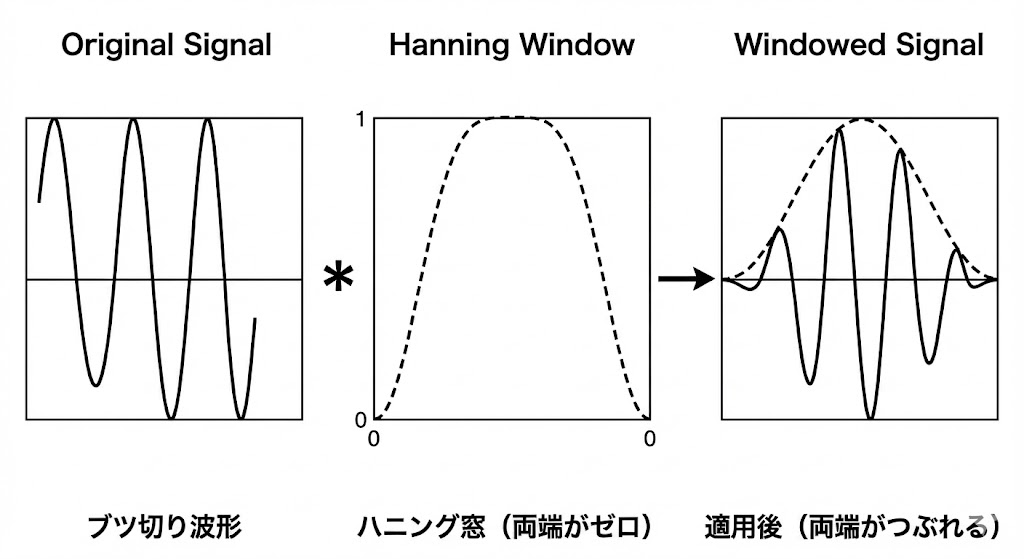
これを防ぐために、「ハニング窓」などの窓関数を掛け合わせます。これはデータの両端を滑らかにゼロに近づける処理で、これによってつなぎ目が綺麗に繋がり、正確な周波数分析が可能になります。
ノイズ除去(逆変換)時の注意点
ハニング窓を使用すると、原理上、データの両端が強制的にゼロに近づいてしまいます。 「異常検知」や「分析」のようにスペクトルを見るだけであれば問題ありませんが、「ノイズ除去」のように波形を元に戻す(逆変換する)場合、両端の音量が消失したまま戻らないという副作用が生じます。
データ量が十分に多く、両端を切り捨てても良い場合は無視できますが、データが短い場合や端まで重要である場合は影響が大きいため、窓を使わないほうが無難なケースもあります。 そのため、本記事に記載するノイズ除去のサンプルプログラムでは、波形の復元性(振幅の維持)を優先し、あえて窓関数は使用していません。
FFTのメリット
1. 「元に戻せる」のが簡単かつ強力(フィルタリング)
これが実務で最も使われる機能です。
fft で周波数成分に分解した後、不要な成分(電源ノイズや高周波のガタつき)だけをゼロにして、ifft(逆変換)で元の波形に戻すことができます。
STFTでも逆変換は可能ですが、FFTは「信号全体に対して一括でフィルタを掛ける」ため、位相ズレなどを気にせず、非常にシンプルかつ強力にノイズを除去できます。
2. 計算がとにかく速い
その名の通り「高速(Fast)」であり、アルゴリズムの計算量は $O(N \log N)$ です。
STFTのように何度も計算を繰り返す必要がないため、巨大なログデータや、計算リソースの限られた組み込み機器(エッジデバイス)でのリアルタイム処理に最適です。
3. AI(機械学習)の特徴量として使いやすい
STFTの結果が「画像(スペクトログラム)」になるのに対し、FFTの結果はシンプルな「数値の配列(スペクトル)」です。
これは、LightGBMやXGBoostなどのテーブルデータ系AIと相性が抜群です。「ピーク周波数」「スペクトルの重心」「帯域ごとのパワー」といった数値を算出(特徴量エンジニアリング)し、異常検知モデルの入力として使うのが王道パターンです。
FFTのデメリット
「ごった煮」になってしまい、時間は分からない
これが最大の弱点です。FFTは、データ全体をミキサーにかけてジュースにするようなものです。
「リンゴとバナナが入っている(成分)」ことは完璧に分かりますが、「最初にリンゴを入れて、10秒後にバナナを入れた」という時間的な順序(ストーリー)は完全に失われます。
「いつ異常が起きたか」を知りたい場合には、FFT単体では無力です。
結論:どう使い分ける?
- 全体的なノイズ除去 / 特徴量を数値で出したい ⇒ FFT(今回の主役)
- 変化の流れ(ストーリー)を画像で見たい ⇒ STFT
- 一瞬の衝撃(スパイク)を見つけたい ⇒ ウェーブレット変換
このように、目的が「成分分析・加工」ならFFT、「時系列の変化監視」ならSTFTやウェーブレット、という使い分けがベストです。
FFTを使ったノイズ除去(周波数フィルタリング)
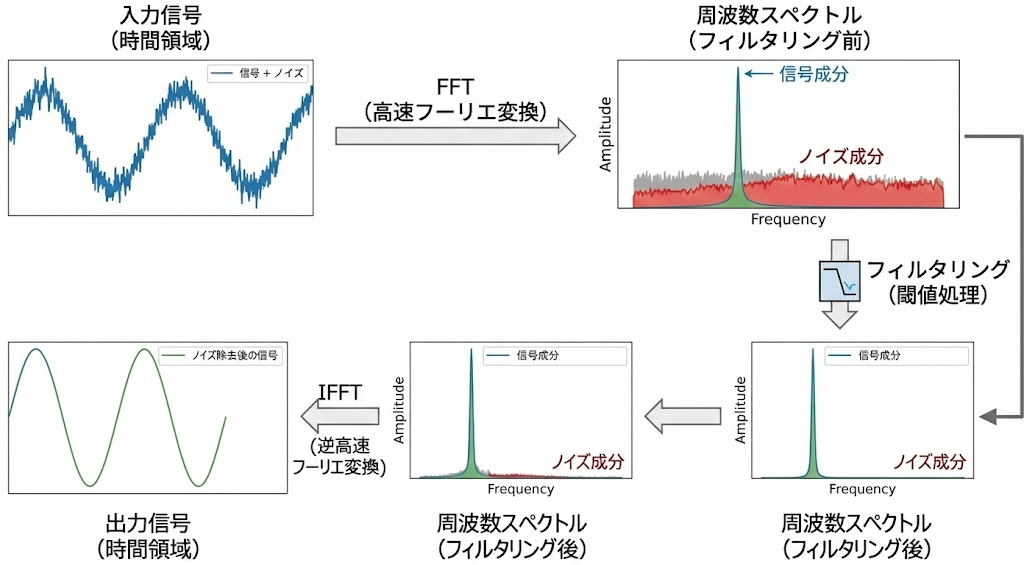
一言でいうと「雑草(ノイズ)を刈り取って、大木(信号)だけ残す」手法です。
- 原理
- 目的の信号(サイン波など)は、FFTスペクトル上で「鋭く高い山」になります。
- 一方でランダムなノイズは、全体に「低く広がる草」のように現れます。
- 処理
- ある高さ(閾値)を決め、それ以下の成分をすべてゼロにします。
- これにより、信号の形を崩さずに、背景の「サーッ」というノイズを一瞬で消し去ることができます。
以下はFFT版のサンプルコードです。STFTよりもコード量が減り、処理も高速です。
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
# 日本語フォント設定
plt.rcParams['font.family'] = 'Meiryo'
def generate_test_data(duration=1.0, fs=1000, freq=50, noise_std=0.5):
"""
テストデータ生成関数
FFT版では「冒頭の無音区間」は必須ではありませんが、比較のため同じデータ構造を作ります。
"""
t = np.linspace(0, duration, int(fs * duration))
# 正解データ(信号)
clean = np.sin(2 * np.pi * freq * t)
# ノイズ
np.random.seed(42)
noise = np.random.normal(0, noise_std, len(t))
# 入力データ
data = clean + noise
return t, clean, data
def fft_noise_filter(data, fs, threshold_ratio=0.3):
"""
FFTによる周波数フィルタリング(閾値処理)
Parameters
----------
data : array_like
入力信号データ。
fs : int
サンプリング周波数。
threshold_ratio : float
閾値の係数(0.0〜1.0)。
「最大振幅の何割以下をノイズとみなすか」を決めます。
0.3 なら、最大パワーの30%以下の成分をすべてカットします。
Returns
-------
cleaned_signal : ndarray
ノイズ除去後の信号データ。
"""
n = len(data)
# 1. FFTで周波数領域へ
# 信号全体を一発で変換します
F = np.fft.fft(data)
freq = np.fft.fftfreq(n, d=1/fs)
# 2. 振幅スペクトルを計算
amp = np.abs(F)
# 3. ノイズの閾値を決定(ここがポイント)
# ここでは「最大ピークの〇〇%」を閾値としますが、
# 「平均値 * 3」など統計的に決める方法もあります。
max_amp = np.max(amp)
threshold = max_amp * threshold_ratio
# 4. フィルタリング(閾値以下の成分をゼロにする)
# Boolean maskを作成: 閾値より大きい場所だけ True
filter_mask = amp > threshold
# マスクを適用(小さい成分はゼロになる)
F_filtered = F * filter_mask
# 5. IFFTで波形に戻す
cleaned_signal = np.fft.ifft(F_filtered)
# 実部だけを取り出して返す
return cleaned_signal.real
def plot_results(t, clean, noisy, denoised):
"""
結果比較プロット関数
"""
plt.figure(figsize=(10, 8))
# --- 1段目:正解データ ---
plt.subplot(3, 1, 1)
plt.plot(t, clean, color='red', linestyle='-', label='正解データ')
plt.title("正解データ(本来の信号)")
plt.ylabel("振幅")
plt.grid(True, alpha=0.3)
plt.legend(loc='upper right')
# --- 2段目:正解データにノイズを加算 ---
plt.subplot(3, 1, 2)
plt.plot(t, noisy, color='gray', alpha=0.8, label='入力データ')
plt.title("正解データにノイズを加算")
plt.ylabel("振幅")
plt.grid(True, alpha=0.3)
plt.legend(loc='upper right')
# --- 3段目:ノイズ除去結果 ---
plt.subplot(3, 1, 3)
plt.plot(t, denoised, color='blue', label='除去後データ')
plt.title("ノイズ除去結果(FFTフィルタリング後)")
plt.xlabel("時間 [s]")
plt.ylabel("振幅")
plt.grid(True, alpha=0.3)
plt.legend(loc='upper right')
plt.tight_layout()
plt.show()
if __name__ == "__main__":
# パラメータ設定
FS = 1000 # サンプリング周波数
# 1. データの準備
t, clean_sig, noisy_sig = generate_test_data(fs=FS, freq=50, noise_std=0.5)
# 2. ノイズ除去の実行
# 最大振幅の30%以下の「弱い成分」をすべてカットします
denoised_sig = fft_noise_filter(noisy_sig, FS, threshold_ratio=0.3)
# 3. 結果の描画
plot_results(t, clean_sig, noisy_sig, denoised_sig)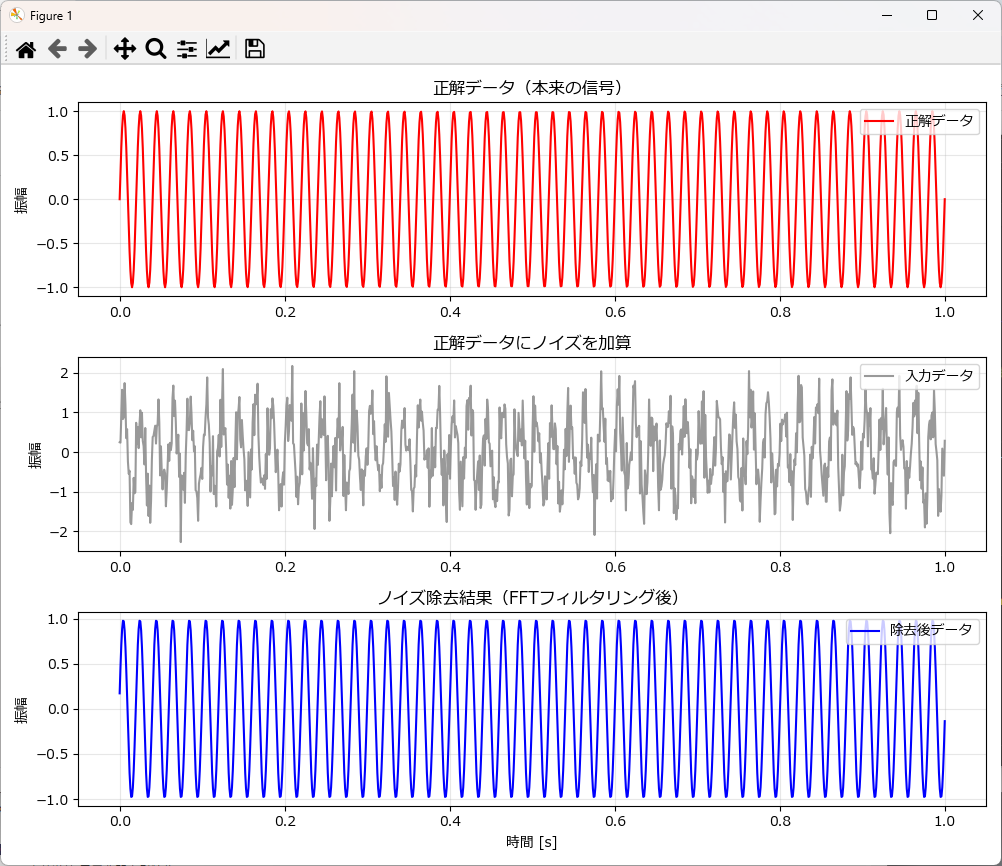
FFTは、今回のような「特定の周波数(50Hz)が強く出ているデータ」に対しては、STFTよりも圧倒的にきれいに(位相ズレなく)ノイズを除去できます。
逆に、音声のような「周波数がコロコロ変わる複雑なデータ」の場合は、必要な音まで消してしまう可能性があるため、STFTの方が有利な場合もあります。
FFTを使った異常検知(スペクトル比較法)
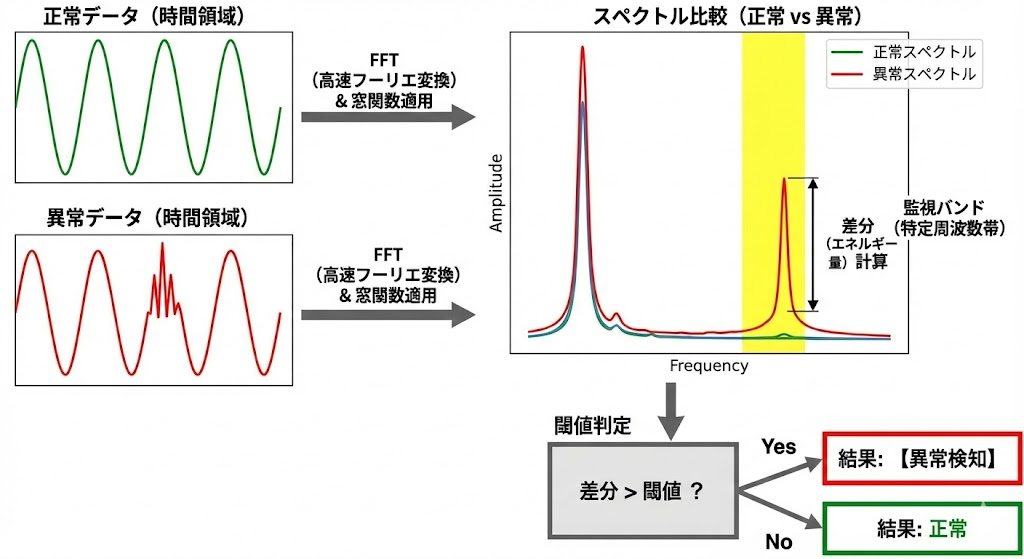
FFTを使った異常検知は、「正常データの形(基準)とのズレを監視する」 という手法が最も一般的で強力です。
単に波形の振幅(音の大きさ)を見るだけでは、「低いゴォーという動作音(正常)」に埋もれて、「キーッという金属音(異常)」が検知できません。 また、STFTのように時間を追う必要がない場合(例:工場の出荷検査で「この製品は不良品か?」を一瞬で判定したい場合)は、FFTを使って「スペクトル全体の形」を比較するほうが、計算が速く、判定基準も明確になります。
異常検知の手順
やり方は非常にシンプルで、以下の4ステップです。
- FFT変換
np.fft.fftを使い、正常データと検査対象データを「周波数ごとの強さ(スペクトル)」に変換します。 - バンド抽出(または全体比較) 異常が発生するであろう「特定の周波数帯(今回は200Hz〜400Hz)」に注目します。
- エネルギー比較(差分計算) 「正常データのエネルギー」と「検査データのエネルギー」を比較します。 もし異常音が混じっていれば、その周波数帯だけエネルギーが跳ね上がっているはずです。
- 閾値判定(良否判定) 差分があらかじめ決めた閾値を超えていれば、「異常(不良品)」と判定します。
本来、閾値の決定には多数のデータからばらつきを計算する「3σ法(3シグマ法)」を用いるのがセオリーです。本記事のコードではデータの用意を簡略化しているため、固定値を用いています。 実務において「正常データのログファイルが1つしかない」という状況で3σ法を適用したい場合は、「時系列スライス」というテクニックを使います。これは、1つの長いデータを短い区間(例:10秒を1秒×10区間)に分割し、サンプル数を擬似的に増やすことで統計量を算出する方法です。
import numpy as np
import matplotlib.pyplot as plt
# 日本語フォント設定
plt.rcParams['font.family'] = 'Meiryo'
def generate_data(duration=2.0, fs=1000, has_anomaly=False):
"""
データ生成関数
has_anomaly=True の場合、50Hzの正常音に加えて、
300Hzの異常音が「一瞬だけ」混入したデータを生成します。
"""
t = np.linspace(0, duration, int(fs * duration))
# 1. 正常信号(50Hzの低い揺れ)
sig = np.sin(2 * np.pi * 50 * t) * 0.5
# 2. 異常信号(300Hzの高い揺れ)
# FFTは「全体」を見るため、一瞬の混入でも「成分」として検出できます
if has_anomaly:
anomaly_period = (t >= 1.0) & (t <= 1.2) # 1.0~1.2秒の間だけ発生
sig[anomaly_period] += np.sin(2 * np.pi * 300 * t[anomaly_period]) * 1.0
# 3. ノイズ(全体にうっすら)
np.random.seed(42)
noise = np.random.normal(0, 0.2, len(t))
return t, sig + noise
def fft_anomaly_score(data, fs, target_band=(200, 400)):
"""
FFTを使って、特定周波数帯のエネルギー量を計算する関数
"""
n = len(data)
# 1. 窓関数の適用(スペクトル漏れ防止)
window = np.hanning(n)
data_windowed = data * window
# 2. FFT実行
F = np.fft.fft(data)
freq = np.fft.fftfreq(n, d=1/fs)
# 振幅スペクトル(データ点数で割って正規化)
amp = np.abs(F) / (n / 2)
# 3. 正の周波数部分だけ取り出す
pos_mask = freq > 0
freq = freq[pos_mask]
amp = amp[pos_mask]
# 4. 監視バンド内のインデックスを抽出
min_f, max_f = target_band
target_idx = np.where((freq >= min_f) & (freq <= max_f))
# 5. バンド内の最大エネルギー(または合計)をスコアとする
# ここでは「その帯域で最も強く出ている成分の高さ」をスコアにします
if len(target_idx[0]) == 0:
score = 0
else:
score = np.max(amp[target_idx])
return freq, amp, score
def plot_comparison(t, normal_data, anomaly_data, normal_res, anomaly_res, threshold):
"""
正常 vs 異常 の比較結果を描画
"""
n_freq, n_amp, n_score = normal_res
a_freq, a_amp, a_score = anomaly_res
plt.figure(figsize=(10, 8))
# --- 1段目:波形比較 ---
plt.subplot(2, 1, 1)
plt.plot(t, normal_data, color='green', alpha=0.6, label='正常データ')
plt.plot(t, anomaly_data, color='red', alpha=0.6, label='異常データ(一瞬だけ混入)')
plt.title("1. 元の波形(重なっていて、目視では違いが分かりにくい)")
plt.ylabel("振幅")
plt.legend(loc='upper right')
plt.grid(True, alpha=0.3)
# --- 2段目:FFTスペクトル比較 ---
plt.subplot(2, 1, 2)
# 正常データのスペクトル
plt.plot(n_freq, n_amp, color='green', alpha=0.5, label=f'正常スペクトル (Score: {n_score:.3f})')
# 異常データのスペクトル
plt.plot(a_freq, a_amp, color='red', alpha=0.8, label=f'異常スペクトル (Score: {a_score:.3f})')
# 監視バンドのエリア表示
plt.axvspan(200, 400, color='yellow', alpha=0.2, label='監視バンド (200-400Hz)')
# 閾値ライン
plt.axhline(threshold, color='blue', linestyle='--', label=f'判定閾値 ({threshold:.3f})')
plt.title("2. FFTスペクトル比較(300Hzに明確な『異常ピーク』が出現)")
plt.xlabel("周波数 [Hz]")
plt.ylabel("振幅")
plt.xlim(0, 500) # 見やすいように500Hzまで拡大
plt.legend(loc='upper right')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
if __name__ == "__main__":
FS = 1000
# 1. データの生成
# 正常データ(学習用:基準を作るためのデータ)
t, normal_data = generate_data(duration=2.0, fs=FS, has_anomaly=False)
# 異常データ(テスト用:300Hzの異常を混ぜたもの)
_, anomaly_data = generate_data(duration=2.0, fs=FS, has_anomaly=True)
# 2. 基準値(閾値)の決定
# まず、正常データだけでスコアを出し「普段の状態」を把握する
normal_res = fft_anomaly_score(normal_data, FS, target_band=(200, 400))
# 「正常データのスコア」に少し余裕(マージン)を持たせた値を閾値にする
# (本来は多数の正常データから統計的に決めますが、今回は簡易的に設定)
normal_score = normal_res[2]
threshold = normal_score + 0.05
# 3. 異常検知の実行
# 決定した閾値を使って、異常データ(未知のデータ)の判定を行う
anomaly_res = fft_anomaly_score(anomaly_data, FS, target_band=(200, 400))
print(f"正常データのスコア: {normal_res[2]:.4f}")
print(f"異常データのスコア: {anomaly_res[2]:.4f}")
print(f"判定閾値: {threshold:.4f}")
if anomaly_res[2] > threshold:
print(">> 判定結果: 【異常検知】(スペクトルに未知のピークがあります)")
else:
print(">> 判定結果: 正常")
# 4. 描画
plot_comparison(t, normal_data, anomaly_data, normal_res, anomaly_res, threshold)正常データのスコア: 0.0261
異常データのスコア: 0.1064
判定閾値: 0.0761
>>判定結果: 【異常検知】(スペクトルに未知のピークがあります)
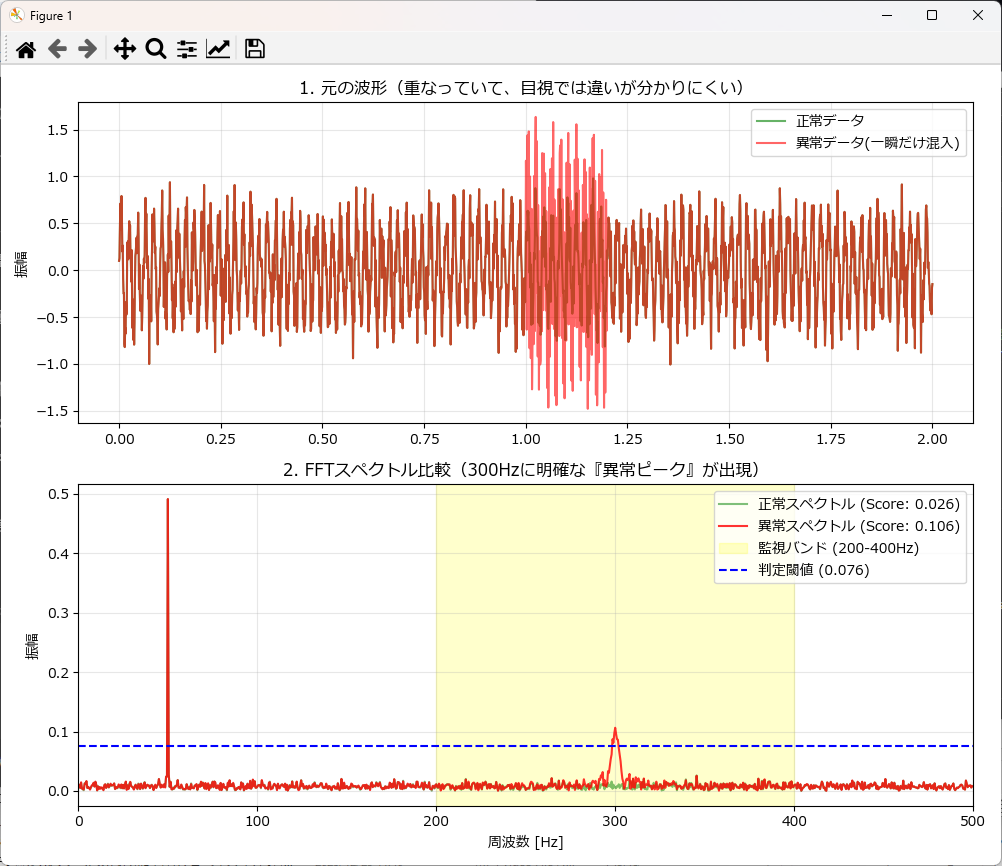
結果の見方(グラフ解説)
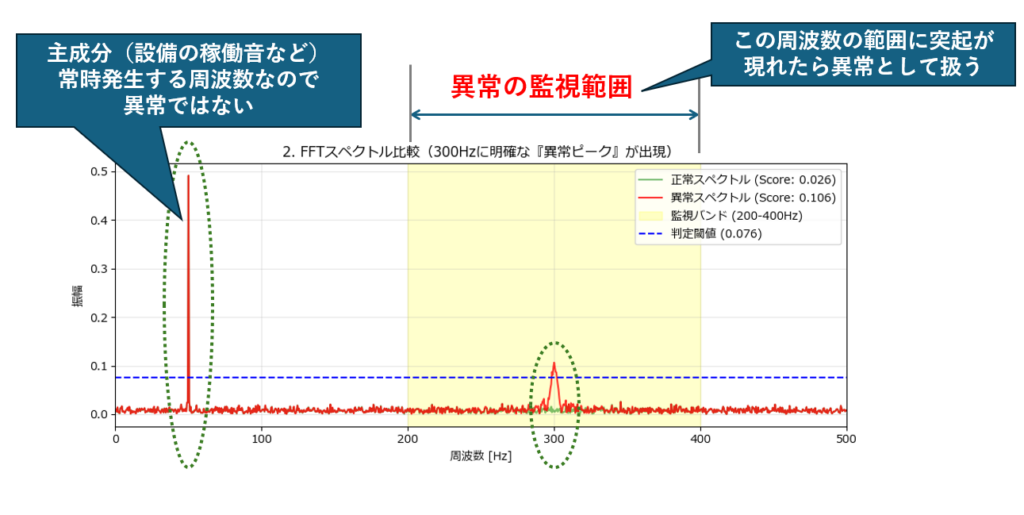
- 緑の線(正常): 左端の50Hz付近に大きな山がありますが、それより右側(高い周波数)はペッタリと平らです。これが「あるべき姿」です。
- 赤の線(異常): 黄色で示した「監視バンド(200Hz〜400Hz)」の中に、一本だけ鋭い赤いトゲ(ピーク)が立っています。 これが、一瞬だけ混入した「300Hzの異常振動」の正体です。
FFTの強みはここにあります。 元の時系列データ(上段のグラフ)では、異常音はわずか0.2秒しか鳴っておらず、見た目では完全にノイズに埋もれています。 しかし、FFTで全体を積分(集計)することで、そのわずかな異常成分が「確実な証拠(ピーク)」として積み上げられ、はっきりと可視化されるのです。
「いつ鳴ったか」は分かりませんが、「この製品には異常な成分が含まれている」ということ(=不良品であること)は、このグラフ一発で確定できます。
周波数スペクトル解析(成分分解)
周波数スペクトル解析は、FFTの最も基本かつ重要な機能です。 一言で言えば、「ごちゃ混ぜになった音のスープから、レシピ(成分表)を復元する」技術です。
STFT(スペクトログラム)が「時間の流れ」を見るのに対し、FFTは時間を無視してデータ全体を要約し、「結局、どの高さの音が、どれくらいの強さで含まれているのか」を可視化します。これを「スペクトル(パワースペクトル)」と呼びます。
- 横軸: 周波数(音の高さ)
- 縦軸: 振幅(音の強さ・エネルギー)
これを使うことで、目で見てもぐちゃぐちゃにしか見えない波形データから、「50Hzの電源ノイズが混じっている」とか「300Hzのモーター回転音が主成分だ」といった正体を一発で見抜くことができます。
import numpy as np
import matplotlib.pyplot as plt
# 日本語フォント設定
plt.rcParams['font.family'] = 'Meiryo'
def plot_spectrum(data, fs, title="FFTスペクトル解析"):
"""
FFTを行い、周波数スペクトル(成分表)を描画する関数
Parameters
----------
data : array_like
解析したい1次元の波形データ。
fs : int
サンプリング周波数 (Hz)。
"""
n = len(data)
# 1. FFT実行(高速フーリエ変換)
# 時間軸のデータを周波数軸のデータに変換します
F = np.fft.fft(data)
# 2. 横軸(周波数)を作成
freq = np.fft.fftfreq(n, d=1/fs)
# 3. 縦軸(振幅)を計算
# np.absで絶対値(大きさ)にし、データ点数 N/2 で割って正規化します
# (正規化しないと、データ数が増えるほど値が巨大になってしまうため)
amplitude = np.abs(F) / (n / 2)
# 4. 表示用に「右半分(正の周波数)」だけを取り出す
# FFTの結果は左右対称になるため、0Hz〜fs/2Hz の範囲だけ見ればOKです
mask = freq > 0
freq_pos = freq[mask]
amp_pos = amplitude[mask]
# 5. 描画
plt.figure(figsize=(10, 6))
plt.plot(freq_pos, amp_pos, color='blue')
plt.title(title)
plt.xlabel('周波数 [Hz]')
plt.ylabel('振幅 (信号の強さ)')
plt.grid(True, alpha=0.3)
# 見やすいように範囲を制限(今回は500Hzまで)
plt.xlim(0, 500)
plt.tight_layout()
plt.show()
# ==========================================
# テストデータの生成と実行
# ==========================================
def generate_composite_data(duration=1.0, fs=1000):
"""
テストデータ生成:
耳で聞くと「ポー」という和音に聞こえるが、波形は複雑なデータ。
1. 50Hz の低い音 (振幅 1.0)
2. 120Hz の高い音 (振幅 0.5)
3. ランダムノイズ
"""
t = np.linspace(0, duration, int(fs * duration))
# 信号1: 50Hz (強い)
sig1 = 1.0 * np.sin(2 * np.pi * 50 * t)
# 信号2: 120Hz (中くらい)
sig2 = 0.5 * np.sin(2 * np.pi * 120 * t)
# ノイズ (弱い)
np.random.seed(42)
noise = np.random.normal(0, 0.2, len(t))
return t, sig1 + sig2 + noise
if __name__ == "__main__":
# パラメータ設定
FS = 1000
# 1. データ生成
t, data = generate_composite_data(duration=1.0, fs=FS)
# 2. 元波形の確認
plt.figure(figsize=(10, 3))
plt.plot(t[:500], data[:500], color='gray', linewidth=0.8) # 見やすくするため最初の0.5秒だけ表示
plt.title("元の波形(波が重なり合って、何Hzか分からない)")
plt.xlabel("時間 [s]")
plt.tight_layout()
plt.show()
# 3. FFTスペクトル解析の実行
plot_spectrum(data, FS, title="【解析結果】FFTスペクトル")解析結果の解説
プログラムを実行すると、以下の2つのグラフが表示されます。
1. 元の波形(時間軸データ)
まず1つ目は、センサーが記録したそのままの波形です。 ご覧の通り、ギザギザした波線が続いているだけで、「この中に何Hzの音が混じっているか?」を目視で判別するのは不可能です。50Hzなのか、60Hzなのか、あるいは複数が混ざっているのか、人間には分かりません。
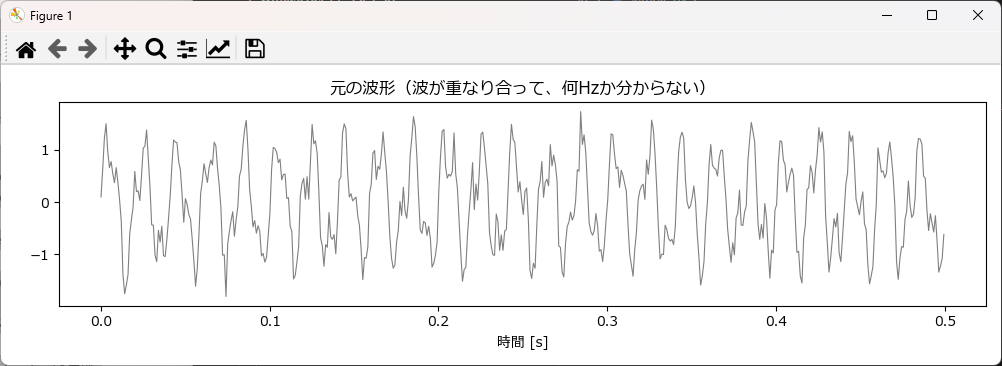
2. FFTスペクトル(周波数軸データ)
2つ目のグラフがFFTの結果です。あれほど複雑だった波形が、驚くほどシンプルな「2本の棒(ピーク)」に変わりました。
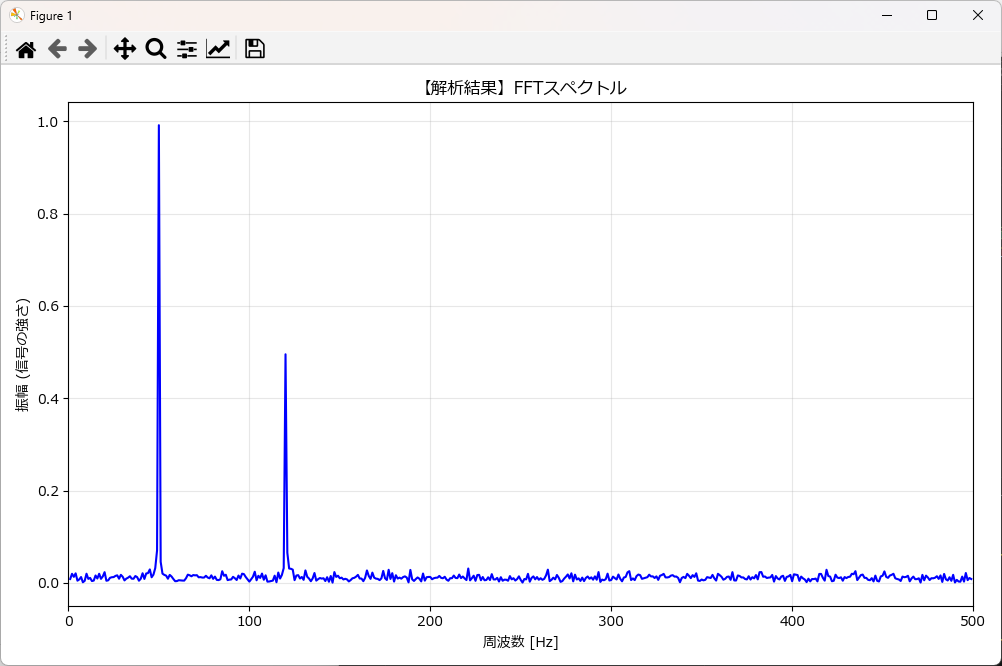
- 左側の高いピーク(50Hz): 横軸が「50」のところで、縦軸(振幅)が「1.0」付近まで伸びています。 → 「ああ、この信号の正体(主成分)は50Hzで、強さは1.0なんだな」 と分かります。
- 右側の低いピーク(120Hz): 横軸が「120」のところで、縦軸が「0.5」付近まで伸びています。 → 「隠し味として120Hzの音が、半分の強さ(0.5)で混ざっているな」 と分かります。
これがFFTの威力です。 「時間の情報」は失われましたが、その代わり「何が含まれているか(成分)」については、これ以上ないほど明確な答えを出してくれます。
異常検知やノイズ除去を行う前に、まずはこのFFTを使って「敵(ノイズや異常音)の周波数は何Hzなのか?」を特定するのが、データ分析の定石(ファーストステップ)となります。
AI前処理(特徴量エンジニアリング)
最近のAI開発では「音をSTFTで画像(スペクトログラム)にして、画像認識AI(CNN)で学習させる」手法が流行っていますが、現場によってはオーバースペックな場合があります。 「GPUがない環境で動かしたい」「判断の根拠(なぜ異常なのか)を知りたい」という場合には、「FFTで数値特徴量(ベクトル)に変換し、軽量なAI(LightGBMやRandomForest)で学習させる」 手法が圧倒的に有利です。
AI学習用の前処理ステップ
FFTを使ったAI開発では、波形データを「画像」にするのではなく、Excelで扱えるような「数値の列(テーブルデータ)」に変換します。これを特徴量エンジニアリングと呼びます。
- FFT変換: 波形をスペクトル(周波数ごとの強さ)に分解する。
- 特徴量抽出: スペクトルから「意味のある数値」を計算する。
- ピーク周波数: 一番音が大きいのは何Hzか?
- ピーク強度: その音の大きさは?
- 重心周波数: 音の高さの平均的な位置はどこか?
- 帯域パワー: 特定の周波数帯(200-400Hzなど)のエネルギー総量は?
- ベクトル化: 計算した数値を横一列に並べて、AIへの入力データ(1行分のレコード)とする。
下記は、波形データから「AIに入力するための数値データ」を生成するサンプルプログラムです。
import numpy as np
import matplotlib.pyplot as plt
# 日本語フォント設定
plt.rcParams['font.family'] = 'Meiryo'
def generate_composite_data(duration=1.0, fs=1000):
"""
テストデータ生成関数
AIに学習させたい「特徴」を含んだ波形を作ります。
ここでは「正常なモーター音(50Hz)」に「異常な金属音(300Hz)」が混ざった状態を模倣します。
"""
t = np.linspace(0, duration, int(fs * duration))
# 信号1: ベースの回転音 (50Hz)
sig1 = 1.0 * np.sin(2 * np.pi * 50 * t)
# 信号2: 異常音 (300Hz)
# これの有無や強さが、AIにとっての判断材料になります
sig2 = 0.5 * np.sin(2 * np.pi * 300 * t)
# ノイズ
np.random.seed(42)
noise = np.random.normal(0, 0.2, len(t))
return t, sig1 + sig2 + noise
def extract_fft_features(data, fs):
"""
音響データをAI(LightGBMなど)学習用に前処理する関数
FFTを行い、スペクトルの形状から「数値特徴量」を算出します。
Parameters
----------
data : ndarray
入力波形データ(1次元)。
fs : int
サンプリング周波数。
Returns
-------
features : dict
抽出された特徴量を格納した辞書。
これをpd.DataFrameなどに変換してAIに入力します。
"""
n = len(data)
# 1. FFT実行
F = np.fft.fft(data)
freq = np.fft.fftfreq(n, d=1/fs)
amp = np.abs(F) / (n / 2) # 振幅スペクトル
# 正の領域だけ抽出
mask = freq > 0
freq = freq[mask]
amp = amp[mask]
# 2. 特徴量抽出 (Feature Engineering)
# ここで「波形の性格」を表す数値を計算します
# (A) ピーク周波数(一番強い成分は何Hzか?)
peak_idx = np.argmax(amp)
peak_freq = freq[peak_idx]
peak_amp = amp[peak_idx]
# (B) スペクトル重心(音の高さの平均的な重心)
# 重心 = Σ(周波数 * 振幅) / Σ(振幅)
spectral_centroid = np.sum(freq * amp) / np.sum(amp)
# (C) 全エネルギー(音の総量)
total_energy = np.sum(amp)
# (D) 特定帯域の強度(例: 200Hz以上の高周波成分の割合)
high_freq_mask = freq > 200
high_freq_energy = np.sum(amp[high_freq_mask])
# 辞書形式でまとめる
features = {
"Peak_Freq_Hz": peak_freq, # ピーク周波数
"Peak_Amp": peak_amp, # ピーク強度
"Centroid_Hz": spectral_centroid,# 重心周波数
"Total_Energy": total_energy, # 全エネルギー
"High_Freq_Energy": high_freq_energy # 高周波成分量
}
return features
# ==========================================
# 実行サンプル
# ==========================================
if __name__ == "__main__":
# パラメータ設定
FS = 1000
DURATION = 1.0
# 1. テストデータ生成
t, wave_data = generate_composite_data(duration=DURATION, fs=FS)
# 2. AI用特徴量抽出の実行
# 波形データ(数千個の数字)が、わずか5個の「意味のある数字」に圧縮されます
features = extract_fft_features(wave_data, FS)
# 3. 結果確認(これがAIへの入力データになります)
print("-" * 40)
print("AI入力用データ (特徴量ベクトル)")
print("-" * 40)
for key, val in features.items():
print(f"{key}: {val:.4f}")
print("-" * 40)
print("※ これを CSVの1行として保存し、LightGBMなどで学習させます。")---------------------------------------------------
AI入力用データ (特徴量ベクトル)
---------------------------------------------------
Peak_Freq_Hz: 50.0000
Peak_Amp: 0.9914
Centroid_Hz: 228.0912
Total_Energy: 7.9178
High_Freq_Energy: 4.4991
---------------------------------------------------
※ これを CSVの1行として保存し、LightGBMなどで学習させます。
なぜこの手法が良いのか?
出力結果を見てください。数千行あった波形データが、たった5つの数値(ピーク周波数、エネルギー等)に要約されました。
- 処理が爆速: 画像処理に比べてデータ量が圧倒的に少ないため、AIの学習・推論が一瞬で終わります。
- 理由が分かる: もしAIが「異常」と判定した場合、「High_Freq_Energy(高周波成分)の値が高かったから異常と判断しました」 というように、エンジニアが納得できる説明(解釈性)が得られます。CNN(画像AI)ではこうはいきません。
「とりあえず画像にしてディープラーニング」と飛びつく前に、まずはFFTで「数値データとして扱えないか?」を検討するのが良いアプローチです。
まとめ
本記事では、信号処理の基本にして最強の武器である FFT(高速フーリエ変換) について、その仕組みからPythonによる実践的な実装までを解説しました。
今回紹介した4つのテクニックは、データ分析の「最初の一歩」として、どのような現場でも必ず役に立つものです。
- 周波数スペクトル解析(成分分解)
- データ全体に「何Hzの成分」が含まれているか、その正体(レシピ)を暴く。
- 強力なノイズ除去(周波数フィルタリング)
- 特定の周波数成分(雑草)を一括で刈り取り、目的の信号(大木)だけをクリアに残す。
- 定常的な異常検知(スペクトル比較)
- 「正常時の形」と「現在の形」を重ね合わせ、未知のピーク(異常成分)の混入を一瞬で判定する。
- AI特徴量抽出(数値化)
- 波形データを「ピーク周波数」や「エネルギー」などの数値ベクトルに要約し、軽量かつ高速なAI(LightGBMなど)に入力できる形にする。
まずは「FFTで全体像を把握(成分分析)」し、そこで時間の変化が重要だと分かったら「STFTで詳細分析」に進む。 この「まずはFFTから」というアプローチこそが、最短距離で正解にたどり着くためのデータ分析の鉄則です。








コメント