【Python実践】SARIMAで時系列データ分析！予測・異常検知・補正を攻略

2025年6月13日2025年6月14日

時系列データには、トレンド（傾向）や季節性（周期的な変動）など、複雑なパターンが含まれることが少なくありません。こうした特徴を捉えるために、より高度なモデルが必要になる場面も多いでしょう。

そこで登場するのが SARIMA（季節調整付きARIMA）モデル です。ARIMAの拡張版として、トレンドと季節性の両方を同時にモデリングできるこの手法は、製造業の需要予測、設備稼働の周期分析、エネルギー使用量の予測など、さまざまな分野で活躍しています。

本記事では、Pythonの statsmodels ライブラリを使って、SARIMAモデルを実装し、予測や異常検知に活用する方法をわかりやすく解説します。

時系列データ分析全般に関する情報、他の手法について知りたい方は、「【Python実践】時系列データ分析で未来予測・異常検知・補正に挑戦！」をご一読ください。

SARIMA（Seasonal ARIMA）とは

SARIMAモデルは、ARIMAモデルに季節性（Seasonal）を組み込んだ時系列解析手法です。ARIMAが非季節性のトレンドや自己相関を扱うのに対し、SARIMAは季節ごとに繰り返す周期的なパターンをモデリングできます。

季節変動を持つデータ（例：月別売上や気温の年間周期など）に適しており、季節要素の分解と予測が同時に可能です。統計的手法のため比較的解釈しやすく、幅広い業種の時系列分析で使われています。

得意な分野

✅ 季節性のある時系列：年間・四半期・月次など周期的なパターンを含むデータの予測に強い。
✅ トレンドと季節性の同時モデリング：トレンド変化と季節変動を分けて扱えるため、精度の高い予測が可能。
✅ 比較的少量のデータでも対応可能：機械学習より少ないデータでモデル構築できる場合が多い。
✅ モデルの解釈性：パラメータが統計モデルの形で表現されるため、理解しやすい。

不得意な分野

❌ 非線形・複雑パターン：線形モデルなので、非線形性や複雑な変動の表現は苦手。
❌ 大量多変量データ：多くの変数を含むデータのモデリングには向かない。
❌ モデル選択の難しさ：季節・非季節の次数設定が多く、適切なパラメータ探索に手間がかかる。
❌ リアルタイム適応：パラメータ更新に時間がかかり、リアルタイム処理には不向きな場合がある。

SARIMAは季節性を考慮した統計的時系列分析の定番モデルとして、多くの業務で使われていますが、非線形な複雑パターンには他の手法（LSTMなど）を検討するのが効果的です。

準備

本記事で紹介しているプログラムを実行する場合、こちらに掲載しているプログラムを実行し、ダミーデータを作成の上、各プログラムの read_csv() のファイル参照パスを適宜変更してください。

また、下記のコマンドで必要なモジュールをインストールしてください。

pip install pandas numpy matplotlib statsmodels

SARIMAモデルによる未来予測

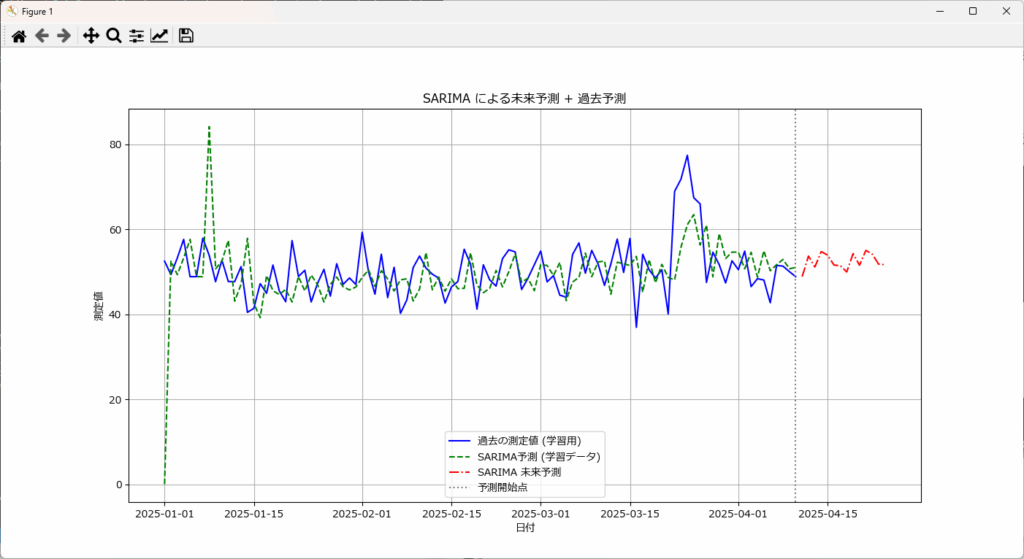
SARIMAモデルは、ARIMAに季節成分を加えた時系列予測手法であり、周期的な変動やトレンドを考慮して未来の値を予測します。

売上や気温など季節性のあるデータの短期予測に適しており、統計モデルとして解釈しやすいのが特徴です。ただし、長期予測や複雑な変動には対応が難しく、パラメータが複雑であること、トレンドの急な変化や非線形な変動には弱いなど、デメリットも存在します。

SARIMAモデルは、order と seasonal_order に与える値によって、予測モデルの性能が大幅に変わります。

model = SARIMAX(
valuess, # ① 対象となる時系列データ
order=(p, d, q), # ② 非季節成分の次数
seasonal_order=(P, D, Q, s) , # ③ 季節成分の次数
enforce_stationarity=False, # ④ 定常性の強制 (通常False)
enforce_invertibility=False # ⑤ 反転可能性の強制 (通常False)
)
model.fit(disp=False)

引数	引数の意味
order=(p ,d ,q)	p：過去の値に対する自己回帰（AutoRegressive, AR）の影響度 d：データを定常化するために取る差分の回数（Integrated, I） q：過去の予測誤差に基づく移動平均（Moving Average, MA）の影響度
seasonal_order=(P, D, Q, s)	P：季節的な自己回帰の影響度（周期ごとの自己回帰） D：季節性を定常化するための差分の回数 Q：季節的な移動平均の影響度（周期ごとの予測誤差） S：季節周期（例えば「月ごとのデータなら s=12」など）

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import statsmodels.api as sm
import warnings

warnings.filterwarnings("ignore")  # 警告を無視

# 日本語フォントの設定
rcParams['font.family'] = 'Meiryo'

def sarima_forecast_future(df: pd.DataFrame, timestamp_col: str, value_col: str, forecast_steps: int = 14):
    """
    SARIMA を使用して未来予測を行い、過去の予測も含める。

    Parameters:
    df (pd.DataFrame): 時系列データの DataFrame。
    timestamp_col (str): タイムスタンプの列名。
    value_col (str): 対象の数値データの列名。
    forecast_steps (int): 未来の予測ステップ（日数単位）。

    Returns:
    pd.DataFrame: 予測結果（過去の予測値・未来の予測値を含む）。
    """

    # 時系列データに変換
    df = df.set_index(timestamp_col)
    df[value_col] = df[value_col].interpolate(method="linear").fillna(method="bfill").fillna(method="ffill")

    # SARIMA モデルの構築
    print(f"\n--- SARIMA による未来予測 ({forecast_steps}日先まで) ---")
    model = sm.tsa.SARIMAX(df[value_col], order=(1, 1, 1), seasonal_order=(1, 1, 1, 7))
    results = model.fit()
    print("SARIMAモデルの学習が完了しました。")

    # 過去の予測値を取得（学習データに対する予測）
    df["yhat_past"] = results.predict(start=0, end=len(df) - 1)

    # 未来予測の生成
    forecast_index = pd.date_range(start=df.index.max(), periods=forecast_steps + 1, freq="D")[1:]  # 未来の日付作成
    forecast_values = results.get_forecast(steps=forecast_steps)
    df_future = pd.DataFrame({
        "timestamp": forecast_index,
        "yhat_future": forecast_values.predicted_mean
    }).set_index("timestamp")

    # 結果のプロット
    plt.figure(figsize=(14, 7))

    # 過去の実測値（青実線）
    plt.plot(df.index, df[value_col], label="過去の測定値 (学習用)", color="blue")

    # 学習データに対する予測（緑点線）
    plt.plot(df.index, df["yhat_past"], label="SARIMA予測 (学習データ)", color="green", linestyle="--")

    # 未来予測（赤点線）
    plt.plot(df_future.index, df_future["yhat_future"], label="SARIMA 未来予測", color="red", linestyle="-.")

    # 予測開始点の縦点線
    forecast_start = df.index.max()
    plt.axvline(x=forecast_start, color="gray", linestyle=":", label="予測開始点")

    # グラフ体裁
    plt.xlabel("日付")
    plt.ylabel("測定値")
    plt.title("SARIMA による未来予測 + 過去予測")
    plt.legend()
    plt.grid(True)
    plt.show()

    # 未来予測だけを返す
    forecast_result = df_future[["yhat_future"]]

    print("予測結果:")
    print(forecast_result)

    return forecast_result

if __name__ == "__main__":
    # データ読み込み
    csv_filename = "dummy_timeseries.csv"
    df = pd.read_csv(csv_filename, parse_dates=["timestamp"])

    # 未来予測の実行
    sarima_predictions = sarima_forecast_future(df, "timestamp", "value", forecast_steps=14)

予測結果:
　　　　　　yhat_future
timestamp
2025-04-11 48.831266
2025-04-12 53.682837
2025-04-13 51.118972
2025-04-14 54.737140
2025-04-15 53.890339
2025-04-16 51.555422
2025-04-17 51.424569
2025-04-18 49.928556
2025-04-19 54.267337
2025-04-20 51.518799
2025-04-21 55.016994
2025-04-22 54.135694
2025-04-23 51.781299
2025-04-24 51.655130

SARIMAモデルによる異常検知

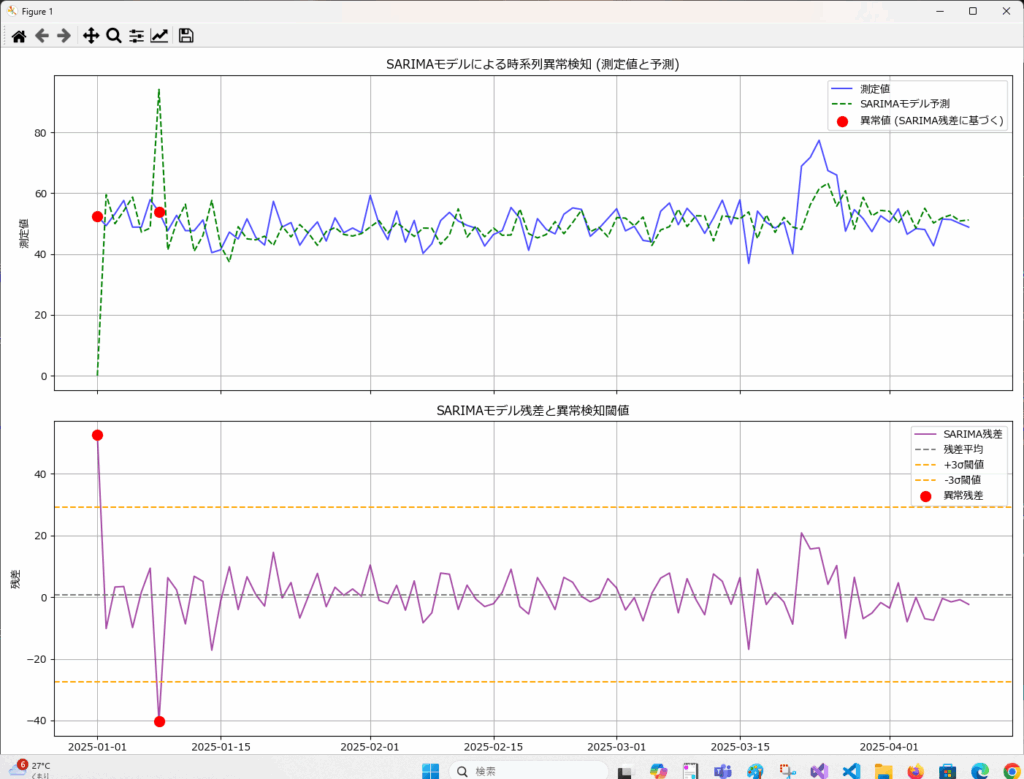
SARIMAは、実際の値と予測値の差（残差）を計算し、残差が閾値（例えば平均±3σ）を超えた場合、異常な変動として検出します。
下記のサンプルプログラムは、 threshold_sigma にσの倍数を指定することで、閾値を指定しています。

import pandas as pd
import numpy as np 
import matplotlib.pyplot as plt
from statsmodels.tsa.statespace.sarimax import SARIMAX
from matplotlib import rcParams

# 日本語フォントの設定 (お使いの環境に合わせて適宜変更してください)
rcParams['font.family'] = 'Meiryo' # Windowsの場合


def sarima_anomaly_detection(df: pd.DataFrame, time_col: str, value_col: str, 
                             order: tuple, seasonal_order: tuple, threshold_sigma: int = 3):
    """
    SARIMAモデルを使用して時系列データの異常検知を行います。
    グラフは縦に並べて表示されます。

    Args:
        df (pd.DataFrame): 処理するデータフレーム。
        time_col (str): タイムスタンプの列名。
        value_col (str): 時系列データの値の列名。
        order (tuple): SARIMAモデルの非季節成分の次数 (p, d, q)。
        seasonal_order (tuple): SARIMAモデルの季節成分の次数 (P, D, Q, s)。
        threshold_sigma (int, optional): 異常値を判断するための残差の標準偏差の倍数。デフォルトは3。

    Returns:
        pd.DataFrame: 'residuals'と'is_anomaly'列が追加されたデータフレーム。
    """
    
    # タイムスタンプ列をインデックスに設定
    df_processed = df.set_index(time_col).copy()

    # SARIMAモデルの適用
    print(f"--- SARIMAモデルの適用: order={order}, seasonal_order={seasonal_order} ---")
    try:
        model = SARIMAX(df_processed[value_col], 
                        order=order, 
                        seasonal_order=seasonal_order, 
                        enforce_stationarity=False, 
                        enforce_invertibility=False)
        model_fit = model.fit(disp=False)
        print("SARIMAモデルの学習が完了しました。")
        # print(model_fit.summary()) # モデルのサマリーを表示したい場合はコメントを解除
    except Exception as e:
        print(f"SARIMAモデルの学習中にエラーが発生しました: {e}")
        return None

    # モデルの残差の計算
    df_processed['residuals'] = model_fit.resid

    # 残差の平均と標準偏差を計算
    residual_mean = df_processed['residuals'].mean()
    residual_std = df_processed['residuals'].std()

    # 異常検知
    df_processed['is_anomaly'] = (df_processed['residuals'] > residual_mean + threshold_sigma * residual_std) | \
                                 (df_processed['residuals'] < residual_mean - threshold_sigma * residual_std)

    # 検出された異常値の表示
    anomalies = df_processed[df_processed['is_anomaly']]
    if not anomalies.empty:
        print("\n--- 検出された異常値 ---")
        print(anomalies[[value_col, 'residuals', 'is_anomaly']])
    else:
        print("\n--- 異常値は検出されませんでした ---")

    # --- 結果の可視化 (グラフを縦に並べる) ---
    fig, axes = plt.subplots(nrows=2, ncols=1, figsize=(14, 10), sharex=True) # 2行1列でグラフを配置

    # 1つ目のサブプロット: 測定値と予測値
    axes[0].plot(df_processed.index, df_processed[value_col], label='測定値', color='blue', alpha=0.7)
    axes[0].plot(df_processed.index, model_fit.predict(start=0, end=len(df_processed)-1), label='SARIMAモデル予測', color='green', linestyle='--')
    
    if not anomalies.empty:
        axes[0].scatter(anomalies.index, anomalies[value_col], color='red', s=100, zorder=5, label='異常値 (SARIMA残差に基づく)')

    axes[0].set_title('SARIMAモデルによる時系列異常検知 (測定値と予測)')
    axes[0].set_ylabel('測定値')
    axes[0].legend()
    axes[0].grid(True)

    # 2つ目のサブプロット: 残差と閾値
    axes[1].plot(df_processed.index, df_processed['residuals'], label='SARIMA残差', color='purple', alpha=0.7)
    axes[1].axhline(residual_mean, color='gray', linestyle='--', label='残差平均')
    axes[1].axhline(residual_mean + threshold_sigma * residual_std, color='orange', linestyle='--', label=f'+{threshold_sigma}σ閾値')
    axes[1].axhline(residual_mean - threshold_sigma * residual_std, color='orange', linestyle='--', label=f'-{threshold_sigma}σ閾値')
    
    if not anomalies.empty:
        axes[1].scatter(anomalies.index, anomalies['residuals'], color='red', s=100, zorder=5, label='異常残差')

    axes[1].set_title('SARIMAモデル残差と異常検知閾値')
    axes[1].set_xlabel('日付')
    axes[1].set_ylabel('残差')
    axes[1].legend()
    axes[1].grid(True)

    plt.tight_layout() # サブプロット間のスペースを自動調整
    plt.show()

    return df_processed

# --- メインの実行部分 ---
if __name__ == "__main__":
    # CSVを読み込んで関数を実行
    # dummy_timeseries.csvが既に存在することを前提とします。
    df = pd.read_csv("dummy_timeseries.csv", parse_dates=["timestamp"])

    # SARIMAモデルのパラメータ (例: 季節周期が7日と仮定)
    # これらのパラメータは、実際のデータの特性に基づいて調整が必要です。
    sarima_order = (1, 1, 1)
    sarima_seasonal_order = (1, 1, 1, 7) 
    
    # 関数を呼び出す
    result_df = sarima_anomaly_detection(df, 
                                          time_col="timestamp", 
                                          value_col="value", 
                                          order=sarima_order, 
                                          seasonal_order=sarima_seasonal_order,
                                          threshold_sigma=3)
    
    if result_df is not None:
        print("\n--- 関数実行結果 (異常値検出フラグ含む) ---")
        print(result_df.tail())

--- 検出された異常値 ---
　　　　　　value residuals is_anomaly
timestamp
2025-01-01 52.483571 52.483571 True
2025-01-08 53.837174 -40.271063 True
--- 関数実行結果 (異常値検出フラグ含む) ---
　　　　　　value residuals is_anomaly
timestamp
2025-04-06 42.682425 -7.502885 False
2025-04-07 51.480601 -0.435379 False
2025-04-08 51.305276 -1.553907 False
2025-04-09 50.025567 -0.836272 False
2025-04-10 48.827064 -2.3634

SARIMAモデルによるデータ補正／クリーニング

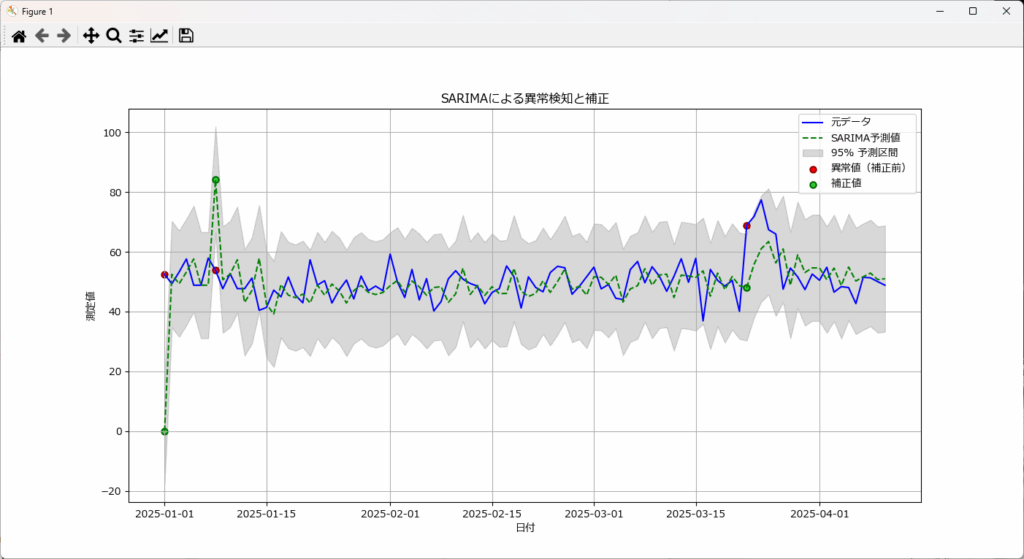
SARIMAで異常検知を行い、検出された「異常値」を「予測値」で置き換えることで、データ補正を行います。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import statsmodels.api as sm
import warnings

warnings.filterwarnings("ignore")
rcParams['font.family'] = 'Meiryo'

def sarima_anomaly_detection_and_cleaning(df: pd.DataFrame,
                                          time_col: str,
                                          value_col: str,
                                          seasonal_period: int = 7,
                                          correction_method: str = "mean"):
    """
    SARIMA を使って異常検知＆補正を行う関数

    Parameters:
        df (pd.DataFrame): 時系列データ
        time_col (str): タイムスタンプ列名
        value_col (str): 測定値の列名
        seasonal_period (int): 季節周期（例: 7なら週次）
        correction_method (str): "mean"（SARIMA予測）または "median"（移動中央値）

    Returns:
        pd.DataFrame: 異常値を補正したデータフレーム
    """

    # 時系列データに変換
    df = df.set_index(time_col)
    df[value_col] = df[value_col].interpolate(method="linear").fillna(method="bfill").fillna(method="ffill")

    # SARIMA モデルの構築と予測
    model = sm.tsa.SARIMAX(df[value_col], order=(1, 1, 1), seasonal_order=(1, 1, 1, seasonal_period))
    results = model.fit()
    df["yhat"] = results.predict(start=0, end=len(df) - 1)

    # 標準偏差を用いた異常値検知
    std_dev = np.std(df[value_col] - df["yhat"])
    df["yhat_lower"] = df["yhat"] - 2 * std_dev
    df["yhat_upper"] = df["yhat"] + 2 * std_dev

    df["is_anomaly"] = (df[value_col] < df["yhat_lower"]) | (df[value_col] > df["yhat_upper"])

    # 異常値補正
    if correction_method == "mean":
        df["corrected"] = df.apply(lambda row: row["yhat"] if row["is_anomaly"] else row[value_col], axis=1)
    elif correction_method == "median":
        rolling_median = df[value_col].rolling(window=7, center=True, min_periods=1).median()
        df["corrected"] = df.apply(lambda row: rolling_median[row.name] if row["is_anomaly"] else row[value_col], axis=1)
    else:
        raise ValueError("correction_method は 'mean' または 'median' のいずれかを指定してください。")

    # 可視化
    plt.figure(figsize=(14, 7))
    plt.plot(df.index, df[value_col], label="元データ", color="blue")
    plt.plot(df.index, df["yhat"], label="SARIMA予測値", color="green", linestyle="--")
    plt.fill_between(df.index, df["yhat_lower"], df["yhat_upper"], color='gray', alpha=0.3, label="95% 予測区間")
    plt.scatter(df.index[df["is_anomaly"]], df[value_col][df["is_anomaly"]], color="red", label="異常値（補正前）", edgecolors="darkred", linewidths=1.5)
    plt.scatter(df.index[df["is_anomaly"]], df["corrected"][df["is_anomaly"]], color="limegreen", label="補正値", edgecolors="darkgreen", linewidths=1.5)

    plt.xlabel("日付")
    plt.ylabel("測定値")
    plt.title("SARIMAによる異常検知と補正")
    plt.legend()
    plt.grid(True)
    plt.show()

    # インデックスを戻す
    df_result = df.reset_index()
    return df_result

# --- 実行例 ---
if __name__ == "__main__":
    try:
        df = pd.read_csv("dummy_timeseries.csv", parse_dates=["timestamp"])
    except FileNotFoundError:
        print("dummy_timeseries.csv not found. Creating a sample dummy_timeseries.csv.")
        dates = pd.to_datetime(pd.date_range(start="2023-01-01", periods=100, freq="D"))
        values = np.sin(np.linspace(0, 20, 100)) * 10 + 50 + np.random.randn(100) * 5
        # 異常値を追加
        values[10] = 100
        values[50] = 10
        values[80] = 120
        df = pd.DataFrame({"timestamp": dates, "value": values})
        df.to_csv("dummy_timeseries.csv", index=False)
        print("dummy_timeseries.csv created.")
        df = pd.read_csv("dummy_timeseries.csv", parse_dates=["timestamp"])

    cleaned_df = sarima_anomaly_detection_and_cleaning(df,
                                                       time_col="timestamp",
                                                       value_col="value",
                                                       seasonal_period=7,  # 週次の周期性
                                                       correction_method="mean")

    print("\n--- 補正後のデータ ---")
    print(cleaned_df.tail())