LSTMは、時系列データの長期依存性を捉えられる特殊なリカレントニューラルネットワーク(RNN)であり、従来のARIMAや指数平滑法では難しい非線形かつ複雑なパターンの予測に強みがあります。
本記事では、ディープラーニングの代表的な時系列解析手法であるLSTM(Long Short-Term Memory)について、基礎知識からPythonでの実装方法、実際の時系列データを用いた予測・異常検知・補正の具体例まで詳しく解説します。
時系列データ分析全般に関する情報、他の手法について知りたい方は、「【Python実践】時系列データ分析で未来予測・異常検知・補正に挑戦!」をご一読ください。

LSTM(Long Short-Term Memory)とは
STMは、リカレントニューラルネットワーク(RNN)の一種で、時系列データや系列データの長期依存関係を学習できる強力なディープラーニングモデルです。通常のRNNが苦手とする「長期間の情報を保持する」問題を、独自のゲート機構によって解決しています。
LSTMは複雑なパターンや非線形な変動も捉えることができ、時系列予測や異常検知、補正など多様なタスクに適用されています。ただし、モデル構築や学習には比較的多くの計算リソースとデータが必要で、パラメータの調整も難しい点があります。
得意な分野
✅ 長期依存性の学習:過去の長期間にわたる影響を考慮できるため、複雑なトレンドやパターンの予測に強い。
✅ 非線形なデータ:複雑で非線形な時系列の関係性を柔軟にモデル化可能。
✅ 多変量時系列:複数の関連する時系列データを同時に扱い、高度な予測や異常検知ができる。
✅ 自動特徴抽出:手動で特徴量を設計しなくても、モデルが重要なパターンを自動的に学習する。
不得意な分野
❌ 少量データ:大量の学習データがないと過学習や性能低下のリスクが高い。
❌ モデルの解釈性:ブラックボックス的な性質が強く、結果の説明や解釈が難しい。
❌ 計算コスト:トレーニングに時間と計算資源がかかるため、リアルタイム処理には不向きな場合もある。
❌ パラメータ調整:ハイパーパラメータが多く、適切な設定には専門知識が必要。
このような特徴を踏まえ、LSTMは複雑で長期的な時系列解析に非常に有効ですが、使いこなすには十分な学習データと計算リソース、そして知識が求められます。
準備
本記事で紹介しているプログラムを実行する場合、こちらに掲載しているプログラムを実行し、ダミーデータを作成の上、各プログラムの read_csv() のファイル参照パスを適宜変更してください。
また、下記のコマンドで必要なモジュールをインストールしてください。
pip install pandas numpy matplotlib scikit-learn tensorflow keras
LSTMのパラメータ
LSTMはディープラーニング(深層学習)モデルであるため、学習時には以下のパラメータ設定が必要です。
特にepochsとbatch_sizeは、深層学習としての学習速度と予測精度に重要な役割を果たしながらも、トレードオフの関係であるため、バランスを取ることが求められます。
| パラメータ | 説明 | 調整のヒント |
|---|---|---|
| sequence_length | 入力データのシーケンス長 | 予測で用いる過去データのウィンドウサイズ。 値が短すぎると情報不足、長すぎると学習負荷増につながる。 過去データに明確な周期性がある場合は、その周期×2~3倍の期間、特定のイベント(メンテナンス日、祝日など)の影響が考えられる場合、その影響期間分が目安となる。 |
| epochs | 学習の反復回数 | データ量に依存するため、大量データでは多めの設定も有り。 少量データの場合は、過学習のリスクがより高まるため、早期停止(early stopping) の活用が有効。 |
| batch_size | 1ステップで処理するサンプル数 | 小さい値にすると、学習は速いが過学習や精度低下の懸念あり。 大きくすると、過学習抑制や精度向上が期待できるが、学習が遅い。 試験的に 16, 32, 64 など異なる値を試すのが効果的。 |
| validation_split | 訓練データから検証データを分割する割合 | 0.1~0.2が一般的。データが少ない場合は検証データを増やすとモデルの汎化性能向上 |
| forecast_steps | 予測する未来のステップ数 | 短すぎると意味がないが、長すぎると誤差が蓄積しやすい。データ特性に合わせて設定 |
epochs の目安は、以下の値を参考に設定します。
大規模データ(数百万サンプル以上)
epochs = 200~500 以上の設定も可能。ただし、モデルが十分学習できるよう、適切な学習率 (learning rate) や batch_size も考慮する。
小規模データ(数千~数万サンプル)
epochs = 50~100 が適切。早期停止を活用し、モデルの過学習を防ぐことが重要。
中規模データ(数十万サンプル程度)
epochs = 100~200 を試しながら調整。データが豊富であれば、より多くの繰り返しが有効。
LSTMモデルの作成
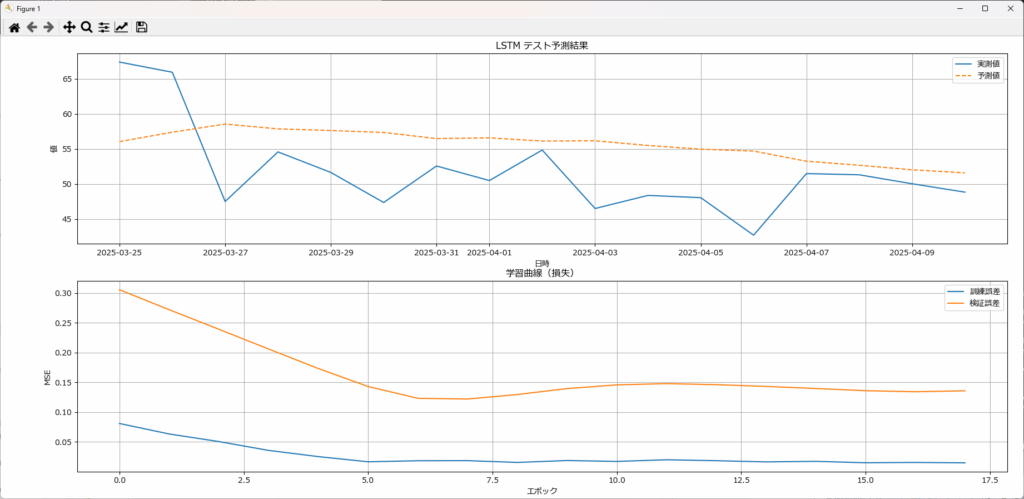
下記のプログラムは、読み込んだCSVファイルのデータを用いてLSTMモデルを作成し、学習済みモデルと学習結果を表示するサンプルプログラムです。
今回のデータは数が少なすぎるため、LSTMでは満足なモデルは作成できませんでしたが、本記事はLSTMの使い方に関する記事であるためご了承ください。
サンプルプログラムは、以下の関数で構成されています。
| 関数名 | 機能 |
|---|---|
| create_and_train_lstm_model | LSTMモデルを構築・学習し、テスト結果を取得 |
| forecast_future | 未来の値を予測 |
| predict_past | 過去のデータをモデルで再予測 |
| detect_anomalies | 予測値と実測値の誤差から異常値を検出 |
| correct_anomalies | 検出された異常値を補正 |
| plot_results | テスト結果と学習曲線を1枚の図に描画 |
このプログラムは、後述する章(未来予測、異常検知、データ補正・クレンジング)で紹介するプログラムの先頭に張り付けて使用しますので、ご承知おきください。
# =========================================================================
# このプログラムは、各章で紹介するプログラムの先頭に張り付けてご使用ください。
# =========================================================================
import pandas as pd
import numpy as np
from sklearn.metrics import mean_squared_error
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM, Dense, Dropout
from tensorflow.keras.callbacks import EarlyStopping
from sklearn.preprocessing import MinMaxScaler
import matplotlib.pyplot as plt
from matplotlib import rcParams
# 日本語フォントの設定
rcParams['font.family'] = 'Meiryo'
def create_and_train_lstm_model(
df: pd.DataFrame,
time_col,
value_col: str,
sequence_length: int = 15,
test_ratio: float = 0.2,
epochs: int = 100,
batch_size: int = 16
) :
"""
LSTMモデルを構築・訓練し、テスト結果と学習曲線も表示。
Args:
df (pd.DataFrame): 時系列データ(タイムスタンプを含む)
time_col (str): タイムスタンプ列の名前
value_col (str): 予測対象の数値データの列名
sequence_length (int, optional): LSTMが参照する過去のデータ長(デフォルト:15)
test_ratio (float, optional): 学習データとテストデータの分割比率(デフォルト:0.2)
epochs (int, optional): モデルの学習回数(デフォルト:100)
batch_size (int, optional): 1回の学習で処理するデータ数(デフォルト:16)
Returns:
model: 学習済みモデル
test_result_df: テストデータの予測結果
scaler: MinMaxScaler(逆変換に使用)
history: 学習履歴(学習曲線描画用)
"""
# タイムスタンプ列をインデックスに設定して並べ替え
df = df.copy()
df.set_index(time_col , inplace=True, drop=True)
df = df.sort_index()
# スケーリング
scaler = MinMaxScaler()
scaled_values = scaler.fit_transform(df[[value_col]])
# シーケンス作成
X, y = [], []
for i in range(len(scaled_values) - sequence_length):
X.append(scaled_values[i : i + sequence_length])
y.append(scaled_values[i + sequence_length])
X, y = np.array(X), np.array(y)
# 学習・テスト分割
split_idx = int(len(X) * (1 - test_ratio))
X_train, X_test = X[:split_idx], X[split_idx:]
y_train, y_test = y[:split_idx], y[split_idx:]
dates = df.index[sequence_length:]
# モデル定義
model = Sequential([
LSTM(50, activation='relu', input_shape=(sequence_length, 1)),
Dropout(0.2),
Dense(1)
])
model.compile(optimizer='adam', loss='mse')
# 学習
early_stopping = EarlyStopping(monitor='val_loss', patience=10, restore_best_weights=True)
history = model.fit(
X_train, y_train,
epochs=epochs,
batch_size=batch_size,
validation_split=0.1,
callbacks=[early_stopping],
verbose=0
)
# 予測・逆変換
y_pred_test = model.predict(X_test, verbose=0).flatten()
y_test_inv = scaler.inverse_transform(y_test.reshape(-1, 1)).flatten()
y_pred_inv = scaler.inverse_transform(y_pred_test.reshape(-1, 1)).flatten()
# RMSE計算
rmse = np.sqrt(mean_squared_error(y_test_inv, y_pred_inv))
print(f"テストRMSE: {rmse:.4f}")
# 結果DataFrame
test_dates = dates[split_idx:]
test_result_df = pd.DataFrame({
'date': test_dates,
'actual': y_test_inv,
'predicted': y_pred_inv
})
return model, test_result_df, scaler, history
def forecast_future(model: Sequential, df: pd.DataFrame, time_col: str, value_col: str,
forecast_days: int, sequence_length: int, scaler: MinMaxScaler) -> pd.DataFrame:
"""
指定した日付以降の未来データをLSTMモデルで予測する。
Args:
model (Sequential): 学習済みLSTMモデル。
time_col (str): タイムスタンプ列の名前
df (pd.DataFrame): 時系列データ(インデックスは日付)。
value_col (str): 予測対象の列名。
forecast_days (int): 予測する日数。
sequence_length (int): LSTMのシーケンス長。
scaler (MinMaxScaler): 正規化用スケーラー。
Returns:
pd.DataFrame: 予測された未来データ(日付, 予測値)。
"""
# タイムスタンプ列をインデックスに設定して並べ替え
df = df.copy()
df.set_index(time_col , inplace=True, drop=True)
df = df.sort_index()
values = df[value_col].values.reshape(-1, 1)
normalized = scaler.transform(values)
# 既存データの最後を使用
future_input = normalized[-sequence_length:].tolist()
future_predictions = []
start_date = df.index.max() + pd.Timedelta(days=1) # 最後の日付の翌日を予測開始点に設定
future_dates = pd.date_range(start=start_date, periods=forecast_days, freq="D")
for _ in range(forecast_days):
x_input = np.array(future_input[-sequence_length:]).reshape(1, sequence_length, 1)
y_pred = model.predict(x_input, verbose=0)
future_predictions.append(y_pred[0][0])
future_input.append([y_pred[0][0]])
forecast_values = scaler.inverse_transform(np.array(future_predictions).reshape(-1, 1)).flatten()
return pd.DataFrame({"date": future_dates, "predicted": forecast_values})
def predict_past(model: Sequential, df: pd.DataFrame, time_col: str, value_col: str,
sequence_length: int, scaler: MinMaxScaler) -> pd.DataFrame:
"""
LSTMモデルを用いて過去データを予測する。
Args:
model (Sequential): 学習済みLSTMモデル。
time_col (str): タイムスタンプ列の名前
df (pd.DataFrame): 時系列データ。
value_col (str): 予測対象の列名。
sequence_length (int): シーケンス長。
scaler (MinMaxScaler): 正規化スケーラー。
Returns:
pd.DataFrame: 実測値と予測値を含むDataFrame(date, actual, predicted)。
"""
# タイムスタンプ列をインデックスに設定して並べ替え
df = df.copy()
df.set_index(time_col , inplace=True, drop=True)
df = df.sort_index()
values = df[value_col].values.reshape(-1, 1)
normalized = scaler.transform(values)
X = []
for i in range(len(normalized) - sequence_length):
X.append(normalized[i:i + sequence_length])
X = np.array(X).reshape(-1, sequence_length, 1)
preds = model.predict(X, verbose=0)
preds_inv = scaler.inverse_transform(preds).flatten()
actual_inv = values[sequence_length:].flatten()
dates = df.index[sequence_length:]
return pd.DataFrame({"date": dates, "actual": actual_inv, "predicted": preds_inv})
def detect_anomalies(pred_df: pd.DataFrame, threshold: float = 2.0) -> pd.DataFrame:
"""
過去予測結果を用いて異常値を検知する(zスコアで判定)。
Args:
pred_df (pd.DataFrame): 実測値と予測値を含むDataFrame。
threshold (float): zスコアの閾値(通常2.0以上)。
Returns:
pd.DataFrame: 異常フラグと誤差列を追加したDataFrame。
"""
pred_df = pred_df.copy()
pred_df["error"] = pred_df["actual"] - pred_df["predicted"]
z_score = (pred_df["error"] - pred_df["error"].mean()) / pred_df["error"].std()
pred_df["anomaly"] = z_score.abs() > threshold
return pred_df
def correct_anomalies(anomalies_df: pd.DataFrame) -> pd.DataFrame:
"""
異常検知結果を基にデータを補正し、新しい列 'corrected' を追加する。
Args:
anomalies_df (pd.DataFrame): 異常検知結果(異常値フラグを含む DataFrame)
Returns:
pd.DataFrame: 異常値を補正した DataFrame(新しい列 'corrected' を追加)
"""
corrected_df = anomalies_df.copy() # 元データをコピー
# 異常値の場合は予測値 (`predicted`)、そうでない場合は実測値 (`actual`) を補正値としてセット
corrected_df["corrected"] = np.where(corrected_df["anomaly"], corrected_df["predicted"], corrected_df["actual"])
return corrected_df
def plot_results(test_df: pd.DataFrame, history) -> None:
"""
テスト予測結果と学習曲線を1枚のシートに上下で表示する関数。
Args:
test_df (pd.DataFrame): テストデータ('date', 'actual', 'predicted'を含む)。
history: 訓練履歴(Kerasの学習履歴オブジェクト)。
Returns:
None: グラフを描画する。
"""
fig, axes = plt.subplots(nrows=2, ncols=1, figsize=(10, 10))
# テスト予測の可視化
axes[0].plot(test_df['date'], test_df['actual'], label='実測値')
axes[0].plot(test_df['date'], test_df['predicted'], label='予測値', linestyle='--')
axes[0].set_title("LSTM テスト予測結果")
axes[0].set_xlabel("日時")
axes[0].set_ylabel("値")
axes[0].legend()
axes[0].grid(True)
# 学習曲線の可視化
axes[1].plot(history.history['loss'], label='訓練誤差')
axes[1].plot(history.history['val_loss'], label='検証誤差')
axes[1].set_title('学習曲線(損失)')
axes[1].set_xlabel('エポック')
axes[1].set_ylabel('MSE')
axes[1].legend()
axes[1].grid(True)
plt.tight_layout() # レイアウト調整
plt.show()
if __name__ == "__main__":
# ダミーデータの読込
df = pd.read_csv("dummy_timeseries.csv", parse_dates=["timestamp"])
# LSTMモデルの作成と学習
model, test_df, scaler, history = create_and_train_lstm_model(
df, time_col="timestamp",value_col="value", sequence_length=15
)
# 学習結果のグラフ化
plot_results(test_df,history)テストRMSE: 7.1109
LSTMによる未来予測
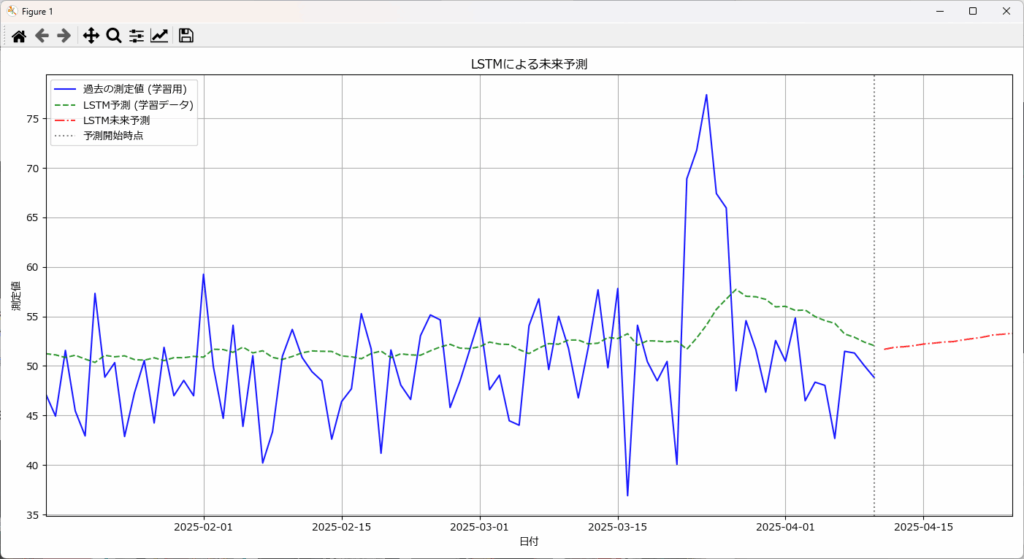
LSTMは、過去の情報を記憶し、活用できるディープラーニングモデルです。このため、複雑な時系列パターンや非線形な変動を学習し、高精度な予測が可能です。
記憶させたい期間は、sequence_length で指定します。今回の例では 15日を指定しているため、データの先頭から15日分のデータが揃う2025/1/15以降に過去分の予測が開始されます。
サンプルデータを使った結果では、過去の測定値と予測値の間に大きな乖離があり、特に変動に対して十分に追従できていないことが見て取れます。また、未来の予測も信頼性に乏しい結果となっています。
この予測精度不足の原因として、sequence_length に指定した15日という値が、データの持つ複雑なパターンや長期的な変動(例:数ヶ月スケールのトレンドや、もし存在するなら季節性)を捉えるには不十分である可能性が考えられます。LSTMは過去の情報を活用できますが、その「窓」であるsequence_lengthが短すぎると、モデルが学習できる文脈が限られてしまい、結果として変動の大きいデータに対する予測が平坦化しやすくなります。
このように、LSTMがある程度のデータ件数、特に学習したい周期性や長期的なトレンドを複数回含むような期間のデータ(例えば、年間の季節性を学習したい場合、最低でも数年分)が無いと、モデルの持つ能力を十分に引き出し、高精度な予測を得ることは困難です。
#========================================================================
# ここに、「LSTMモデルの作成」で紹介したプログラムを張り付けてください。
#========================================================================
def plot_lstm_predictions(df: pd.DataFrame, past_df: pd.DataFrame, future_df: pd.DataFrame, value_col: str) -> None:
"""
LSTMの過去予測・未来予測を統合してプロットする関数。
Args:
df (pd.DataFrame): 元の時系列データ(実測値)
past_df (pd.DataFrame): LSTMによる過去の予測結果
future_df (pd.DataFrame): LSTMによる未来予測結果
value_col (str): 予測対象の列名
Returns:
None: グラフを描画する。
"""
# 日付データの型を統一
past_df["date"] = pd.to_datetime(past_df["date"])
future_df["date"] = pd.to_datetime(future_df["date"])
plt.figure(figsize=(14, 7))
# 過去の測定値(青色)
plt.plot(df["timestamp"], df[value_col], label="過去の測定値 (学習用)", color="blue", alpha=0.9)
# LSTM学習データの予測(緑の破線)
plt.plot(past_df["date"], past_df["predicted"], label="LSTM予測 (学習データ)", color="green", linestyle="--", alpha=0.8)
# 未来のLSTM予測(赤の破線)
plt.plot(future_df["date"], future_df["predicted"], label="LSTM未来予測", color="red", linestyle="-.", alpha=0.8)
# 予測開始点(縦の点線)
prediction_start = past_df["date"].iloc[-1]
plt.axvline(x=prediction_start, color="gray", linestyle=":", label="予測開始時点")
# X軸の範囲を設定(過去の異常値を排除)
plt.xlim(past_df["date"].min(), future_df["date"].max())
plt.title("LSTMによる未来予測")
plt.xlabel("日付")
plt.ylabel("測定値")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
if __name__ == "__main__":
# ダミーデータの読込
df = pd.read_csv("dummy_timeseries.csv", parse_dates=["timestamp"])
# LSTMモデルの作成と学習
model, test_df, scaler, history = create_and_train_lstm_model(
df, time_col="timestamp",value_col="value", sequence_length=15
)
# 過去予測
past_df = predict_past(model=model, df=df, time_col="timestamp",value_col="value", sequence_length=15, scaler=scaler)
print(past_df)
# 未来予測
future_df = forecast_future(model=model, df=df, time_col="timestamp",value_col="value", forecast_days=14, sequence_length=15, scaler=scaler)
print(future_df)
# 未来予測グラフの表示
plot_lstm_predictions(df, past_df, future_df, value_col="value") date actual predicted
0 2025-01-16 47.188562 50.851646
1 2025-01-17 44.935844 50.705032
2 2025-01-18 51.571237 50.365494
3 2025-01-19 45.459880 50.703480
~~~省略~~~
date predicted
0 2025-04-11 51.698261
1 2025-04-12 51.960846
2 2025-04-13 52.117828
3 2025-04-14 52.314560
4 2025-04-15 52.562019
~~~省略~~~
LSTMによる異常検知
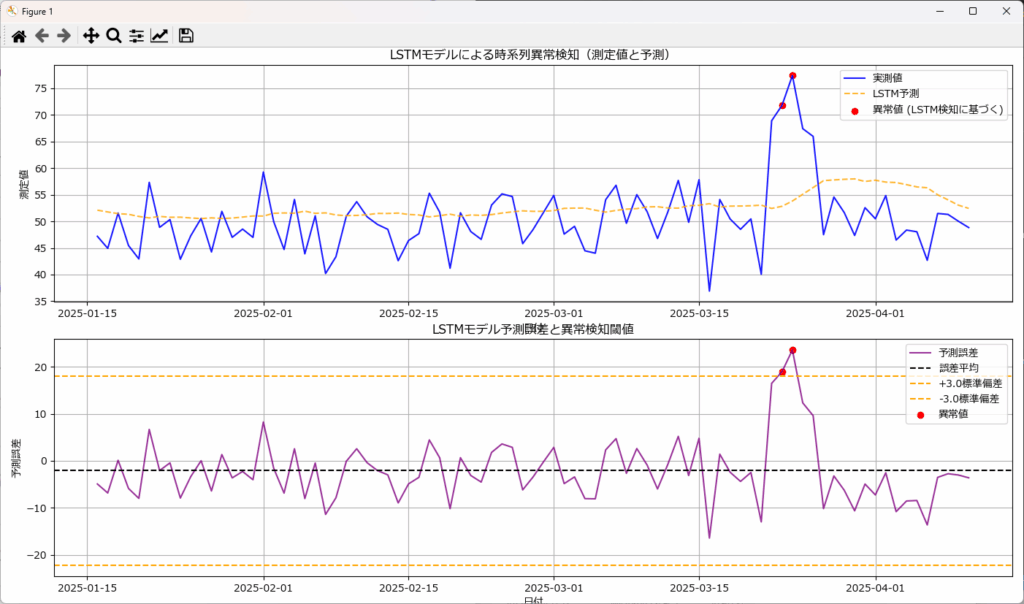
LSTMは、学習結果を元に予測した値と測定値との差=予測誤差(再構築誤差)が大きい場合に異常と判断します。
従来の統計モデル(ARIMA, ES, Prophet)と比較して、LSTMは長期的な依存関係をより詳細に学習でき、非線形な変化にも柔軟に対応可能です(例:SARIMAよりも複雑な変動に対応)。しかし、その計算負荷の高さから、リアルタイムでの異常検知には不向きな場合があります。
LSTMは、事前に学習した正常なデータパターンに基づいて予測モデルを構築します。このため、学習データに異常値が混入していると、モデルが異常を正常と誤認識するリスクがあるため、クリーンな学習データが不可欠です。
また、閾値の設定には、予測誤差の統計的特性(平均、標準偏差)に基づく方法のほか、ヒストグラム分析、パーセンタイル、または教師なし学習アルゴリズム(例:One-Class SVM, Isolation Forestなどと組み合わせて、異常スコアの分布から自動的に閾値を決定する方法)を用いることもあります。
#========================================================================
# ここに、「LSTMモデルの作成」で紹介したプログラムを張り付けてください。
#========================================================================
def plot_anomalies_and_errors(df: pd.DataFrame, anomalies_df: pd.DataFrame) -> None:
"""
LSTMモデルによる異常検知と予測誤差をプロットする関数。
Args:
df (pd.DataFrame): 実測値と予測値を含む元データ
anomalies_df (pd.DataFrame): 異常値を含むDataFrame
Returns:
None: グラフを描画する。
"""
plt.figure(figsize=(14, 12))
# 上段:測定値・予測値・異常値のプロット
plt.subplot(2, 1, 1)
plt.plot(df["date"], df["actual"], label="実測値", color="blue", alpha=0.9)
plt.plot(df["date"], df["predicted"], label="LSTM予測", color="orange", linestyle="--", alpha=0.8)
# 異常値(赤点)
anomalies = anomalies_df[anomalies_df["anomaly"]]
plt.scatter(anomalies["date"], anomalies["actual"], label="異常値 (LSTM検知に基づく)", color="red", marker="o")
plt.title("LSTMモデルによる時系列異常検知(測定値と予測)")
plt.xlabel("日付")
plt.ylabel("測定値")
plt.legend()
plt.grid(True)
# 下段:予測誤差と異常検知閾値
plt.subplot(2, 1, 2)
plt.plot(df["date"], df["actual"] - df["predicted"], label="予測誤差", color="purple", alpha=0.8)
# 誤差の平均値
mean_error = (df["actual"] - df["predicted"]).mean()
plt.axhline(mean_error, color="black", linestyle="--", label="誤差平均")
# ±3標準偏差閾値
std_error = (df["actual"] - df["predicted"]).std()
plt.axhline(mean_error + 3 * std_error, color="orange", linestyle="--", label="+3.0標準偏差")
plt.axhline(mean_error - 3 * std_error, color="orange", linestyle="--", label="-3.0標準偏差")
# 異常値(赤点)
plt.scatter(anomalies["date"], anomalies["actual"] - anomalies["predicted"], label="異常値", color="red", marker="o")
plt.title("LSTMモデル予測誤差と異常検知閾値")
plt.xlabel("日付")
plt.ylabel("予測誤差")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
if __name__ == "__main__":
# ダミーデータの読込
df = pd.read_csv("dummy_timeseries.csv", parse_dates=["timestamp"])
# LSTMモデルの作成と学習
model, test_df, scaler, history = create_and_train_lstm_model(
df, time_col="timestamp",value_col="value", sequence_length=15
)
# 過去予測
past_df = predict_past(model=model, df=df, time_col="timestamp",value_col="value", sequence_length=15, scaler=scaler)
# 異常検知
anomalies_df = detect_anomalies(past_df,3)
print(anomalies_df)
# 異常検知結果と誤差のグラフ化
plot_anomalies_and_errors(past_df,anomalies_df) date actual predicted error anomaly
0 2025-01-16 47.188562 52.100792 -4.912230 False
1 2025-01-17 44.935844 51.765560 -6.829716 False
2 2025-01-18 51.571237 51.449734 0.121503 False
3 2025-01-19 45.459880 51.322826 -5.862947 False
4 2025-01-20 42.938481 50.921665 -7.983184 False
.. … … … … …
80 2025-04-06 42.682425 56.305847 -13.623422 False
81 2025-04-07 51.480601 54.998142 -3.517541 False
82 2025-04-08 51.305276 54.039856 -2.734580 False
83 2025-04-09 50.025567 53.036396 -3.010829 False
84 2025-04-10 48.827064 52.435402 -3.608338 False
LSTMによるデータ補正・クリーニング
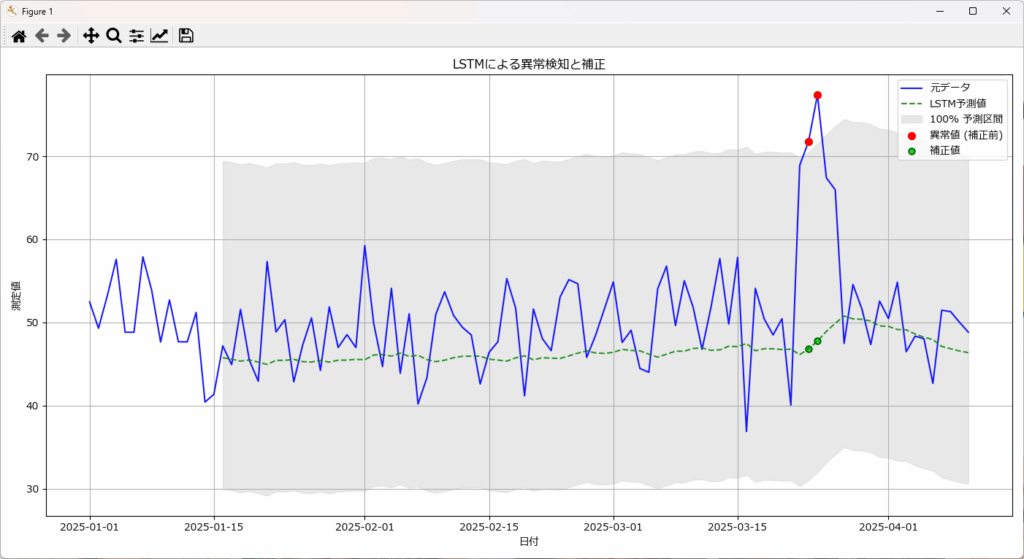
LSTMで異常と判断されたデータを、予測値(最も可能性の高い正常な値)で置き換えることで、データ補正・クリーニングを行います。これは、LSTMが正常なデータパターンを学習しているためです。
逆に、モデルが適切に正常パターンを学習できていない場合や、異常が長期にわたる場合は、補正の精度が低下する可能性があります。
サンプルプログラムでは、plot_anomalies関数で上記のグラフを表示しています。
異常検知の関数detect_anomaliesで指定した閾値(σの倍数)をplot_anomaliesの第2引数に指定することで、閾値の範囲を薄いグレー表示します。第2引数を省略すると、95%信頼区間が表示されます。
#========================================================================
# ここに、「LSTMモデルの作成」で紹介したプログラムを張り付けてください。
#========================================================================
def plot_anomalies(corrected_df: pd.DataFrame, threshold: float = None) -> None:
"""
異常値を検知し、補正後の値を比較するグラフを描画する関数(閾値 or 信頼区間付き)。
Args:
corrected_df (pd.DataFrame): 異常検知済みデータ(補正値は描画しない)
threshold (float, optional): 異常検知に使用するσ値(例: 2.0, 3.0, 3.5)。
Noneの場合は信頼区間(±1.96σ)を表示。
Returns:
None: グラフを描画する。
"""
plt.figure(figsize=(14, 7))
# 実測値(青線)
plt.plot(corrected_df["date"], corrected_df["actual"], label="元データ", color="blue", alpha=0.7)
# LSTM予測値(緑の破線)
plt.plot(corrected_df["date"], corrected_df["predicted"], label="LSTM予測値", color="green", linestyle="--", alpha=0.8)
if threshold is not None:
# 🔹 異常検知閾値(±thresholdσ)
std_error = corrected_df["error"].std()
mean_error = corrected_df["error"].mean()
lower_bound = corrected_df["predicted"] + (mean_error - threshold * std_error)
upper_bound = corrected_df["predicted"] + (mean_error + threshold * std_error)
label_text = f"異常検知閾値 (±{threshold}σ)"
else:
# 🔹 信頼区間(±1.96σ, 95% CI)
std_predicted = corrected_df["predicted"].std()
lower_bound = corrected_df["predicted"] - 1.96 * std_predicted
upper_bound = corrected_df["predicted"] + 1.96 * std_predicted
label_text = "95% 信頼区間 (±1.96σ)"
# 閾値 or 信頼区間をグレーの領域で表示
plt.fill_between(corrected_df["date"], lower_bound, upper_bound, color="gray", alpha=0.2, label=label_text)
# 異常値(赤点)
anomalies = corrected_df[corrected_df["anomaly"]]
plt.scatter(anomalies["date"], anomalies["actual"], label="異常値",
color="red", marker="o", zorder=3)
# 異常値の補正結果(緑点)
plt.scatter(anomalies["date"], anomalies["predicted"], label="補正後の異常値",
color="limegreen", marker="o", edgecolors="darkgreen", linewidths=1.5, zorder=3)
plt.title(f"LSTMによる異常検知と {'閾値' if threshold else '信頼区間'} の範囲")
plt.xlabel("日付")
plt.ylabel("測定値")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
if __name__ == "__main__":
# ダミーデータの読込
df = pd.read_csv("dummy_timeseries.csv", parse_dates=["timestamp"])
# LSTMモデルの作成と学習
model, test_df, scaler, history = create_and_train_lstm_model(
df, time_col="timestamp",value_col="value", sequence_length=15
)
# 過去予測
past_df = predict_past(model=model, df=df, time_col="timestamp",value_col="value", sequence_length=15, scaler=scaler)
# 異常検知
anomalies_df = detect_anomalies(past_df,3)
# データ補正
correct_df = correct_anomalies(anomalies_df)
print(correct_df)
# 異常検知結果と補正結果のグラフ
plot_anomalies(correct_df,3) date actual predicted error anomaly corrected
0 2025-01-16 47.188562 51.863106 -4.674543 False 47.188562
1 2025-01-17 44.935844 51.674099 -6.738255 False 44.935844
2 2025-01-18 51.571237 51.534164 0.037072 False 51.571237
3 2025-01-19 45.459880 51.471390 -6.011510 False 45.459880
4 2025-01-20 42.938481 51.202171 -8.263690 False 42.938481
.. … … … … … …
80 2025-04-06 42.682425 54.555984 -11.873559 False 42.682425
81 2025-04-07 51.480601 53.834969 -2.354367 False 51.480601
82 2025-04-08 51.305276 53.215916 -1.910639 False 51.305276
83 2025-04-09 50.025567 52.555656 -2.530089 False 50.025567
84 2025-04-10 48.827064 52.125526 -3.298462 False 48.827064
plot_anomaliesの第2引数を省略すると、下図の通り95%信頼区間が薄いグレーで表示されます。
# 異常検知結果と補正結果のグラフ
plot_anomalies(correct_df)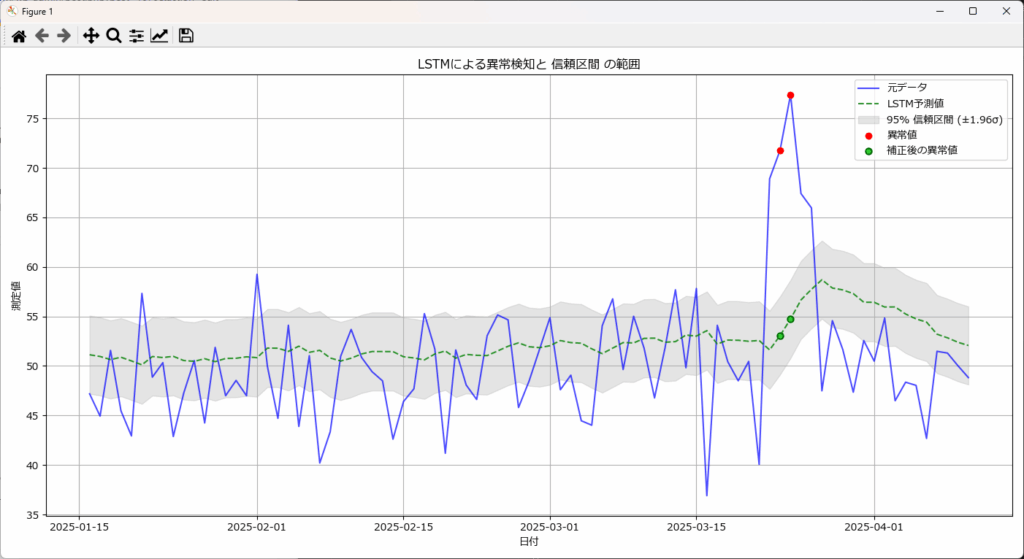
まとめ
本記事では、LSTMの基本的な仕組みからモデル構築・学習の方法、そしてPythonを用いた実践的な時系列データへの応用例まで解説しました。
LSTMは長期的な時系列の依存関係を効果的に捉えることができ、複雑で非線形なデータの予測や異常検知、データ補正に非常に有用な手法です。
TensorFlowやPyTorchを使うことで、実務に即したモデルを比較的容易に構築でき、多くの業界で幅広く応用されています。
これまでの統計的手法や単純な機械学習モデルでは難しかった課題に挑戦するために、ぜひLSTMを活用してみてください。








コメント