センサーデータやログデータなど、日々蓄積される大量の時系列データには、装置の異常兆候、環境の変化、ユーザー行動のパターンなど、重要な“傾向”が潜んでいます。
しかし、何億・何十億行にも及ぶデータをそのまま可視化するのは現実的ではありません。メモリに載らず、描画も重く、全体像が見えなくなります。
本記事では、大量データの中から傾向をつかむために、データを軽量化し、グラフで俯瞰するという実践的なアプローチを紹介します。
SQLiteなどの軽量なデータベースを活用し、時間ブロックやセンサー単位で統計サマリ(平均・分散・最大・最小など)を抽出。Pythonを使って、メモリに載るサイズに圧縮された“意味あるデータ”を可視化することで、膨大な時系列データの中から本質的な傾向を捉える方法を解説します。
本記事で扱う大量データとは
本記事では、数十GB以上・数百センサー規模のセンサーデータを対象に、傾向をつかむための統計的可視化手法を紹介します。
一般的に、分析で扱うセンサーデータには、次のような特徴があります。
- 記録頻度が非常に高い
たとえばCANデータでは、ミリ秒単位(1ms〜10ms)で記録されることも珍しくありません。1秒間に数百件のレコードが生成されることもあります。 - センサーの種類が多い
実際のシステムでは、数百種類のセンサーが同時に記録されるケースもあり、1レコードあたりの変数数が100〜300を超えることもあります。 - 蓄積量が膨大
1台の装置から1日で5〜10GB以上、数週間で数十〜数百GBに達することもあり、メモリに載らないサイズになるのが常態です。
特に複数台の装置や長期間のログを扱う場合、数億〜数十億行規模になることもあります。
こうしたデータは、CSVやExcelで開いて眺めるといった従来の方法では扱いきれません。
また、pandasで全件を読み込んで可視化することも現実的ではなく、元の分布が壊れないように軽量化(サンプリング)することが不可欠です。
大量データの軽量化(サンプリング)手法
すべてのデータを読み込むことが困難な状況でも、適切なサンプリングや抽出を行うことで、元の分布を維持しつつ、分布特性や異常傾向を把握することは可能です。代表的な軽量化手法として、以下のようなサンプリングが有効です。
| 手法名 | 方法の概要 | 主な目的 | メリット | 注意点・取りこぼしリスク |
|---|---|---|---|---|
| 先頭区間抽出 | 先頭から一定件数(例:1000万件)を抽出 | 初期設計・高速な試行 | 実装が簡単、読み込みが速い | 初期に偏りがあると代表性に欠ける |
| 間引き(ダウンサンプリング) | 一定間隔でデータを間引く(例:1秒ごとに1件) | 時間的な均等性の確保 | 高速・軽量、実装が簡単 | ピークや外れ値を見逃す可能性あり |
| 無作為抽出(ランダムサンプリング) | 全体から無作為に抽出 | 分布の代表性を確保 | 偏りが少なく、分布を反映しやすい | 時系列の流れやピークを見逃す可能性あり |
| 層化抽出(ストラティファイドサンプリング) | 時間帯やカテゴリごとに均等に抽出 | 群間の偏りを防ぐ | 時系列や属性のバランスを保てる | 層の設計が必要、実装がやや複雑 |
このような手法を用いて軽量化することにより、Excelやpythonを用いてヒストグラムや箱ひげ図など、様々なグラフによる可視化できるようになります。
先頭区間抽出
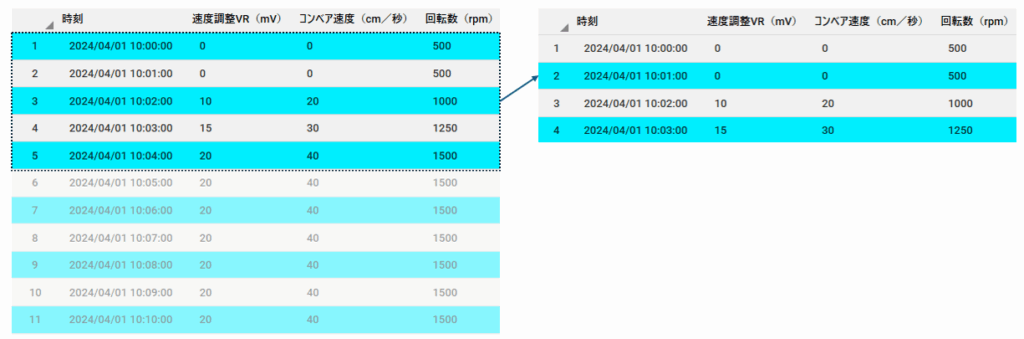
大量データを扱う際、最も手軽に試せるのが「先頭から一定件数を抽出する」方法です。
たとえば、1億行のセンサーデータのうち、先頭から100万件だけを読み込めば、メモリ負荷を大幅に軽減し、可視化や統計処理を高速に試すことができます。
- 例:起動直後のセンサーが不安定な場合、先頭データに異常が集中しており、分布が歪んで見える
- 例:時間とともに環境が変化する場合、初期データだけでは全体傾向を捉えきれない
この方法は初期設計やプロトタイピングに非常に有効ですが、代表性に偏りがある可能性があるという注意点があります。
そのため、先頭抽出を使う前に、以下のような条件を確認することが重要です
- データが定常状態で始まっている(例:安定稼働中の装置ログ)
- 初期区間が全体の代表になり得る(例:短時間のログで、時間変化が少ない)
- 分布の偏りが少ないことを確認済み(例:ヒストグラムで初期と全体を比較済み)
このような場合に限り、先頭からN件抽出は、軽量かつ高速な初期可視化手法として非常に有効です。
特に、ビン推定や統計サマリの初期設計においては、まずこの方法で試してみるのが実務的です。
間引き(ダウンサンプリング)

大量データを可視化する際、最も直感的に思いつくのは「間引き(サンプリング)」です。
たとえば、1msごとに記録されたデータを1秒ごとに1件だけ抽出すれば、データ量は1/1000に減り、描画も軽くなります。
この方法は軽量化に非常に有効ですが、ピーク値や異常値を取りこぼす可能性があるという重大な欠点があります。
- 例:1秒間に急激なスパイクが発生しても、間引き対象のタイミングに含まれなければ見逃してしまう
- 例:周期的な変動の山や谷が、間引きのタイミングとズレていると、傾向が平坦に見えてしまう
そのため、単純間引きを使う前に、あらかじめ分布を確認することが重要です。
- ピークが存在しない(例:安定した温度センサー)
- ピークを無視しても問題ない(例:平均値だけで十分な用途)
- 分布が滑らかで、間引きによる情報損失が少ない
このような場合に限り、単純間引きは有効な選択肢となります。
ランダムサンプリング
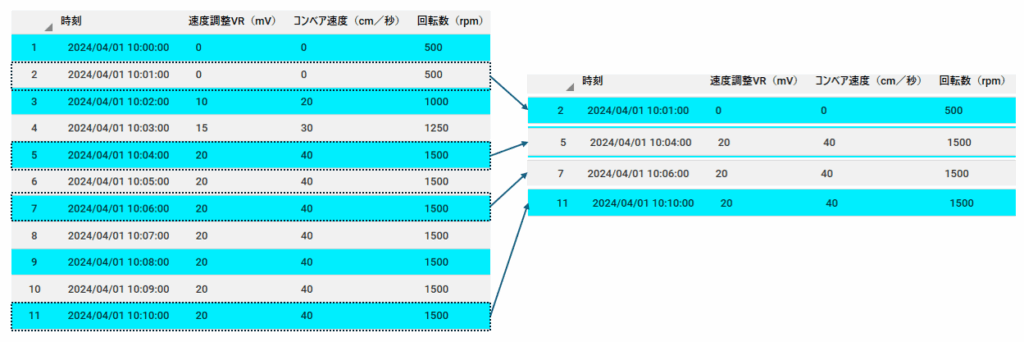
大量データの中から代表性の高いサンプルを抽出したいとき、最も基本的かつ汎用的な手法が「ランダムサンプリング」です。
たとえば、1億行のセンサーデータからランダムに1万件を抽出すれば、全体の分布を比較的忠実に反映した軽量データが得られます。
この方法は、分布の偏りを抑えつつ、メモリに載るサイズで可視化や統計処理を行いたい場合に非常に有効です。
- 例:多峰性や裾の広がりを持つ分布でも、ランダム抽出ならそれらを含む可能性が高い
- 例:異常値やピークが全体に散在している場合、ランダム抽出で一部を捉えられる可能性がある
ただし、時系列の流れや周期性を見たい場合には不向きです。
ランダム抽出では時間軸がバラバラになるため、時系列の傾向や変化を可視化するには適していません。
そのため、ランダムサンプリングを使う前に、以下のような条件を確認することが重要です。
- 時系列の流れよりも、分布の形状(偏り・外れ値・多峰性)を重視したい
- 全体の傾向をざっくり把握したいが、初期区間や特定時間帯に偏りたくない
- 可視化や統計処理の対象が「値の分布」であり、「時間の変化」ではない
このような場合に限り、ランダムサンプリングは、分布代表性を保ちつつ軽量化する手法として非常に有効です。
特に、ヒストグラムのビン推定や分位点の初期設計においては、先頭抽出よりも信頼性の高い結果が得られることが多いです。
ストラティファイドサンプリング(層化抽出)
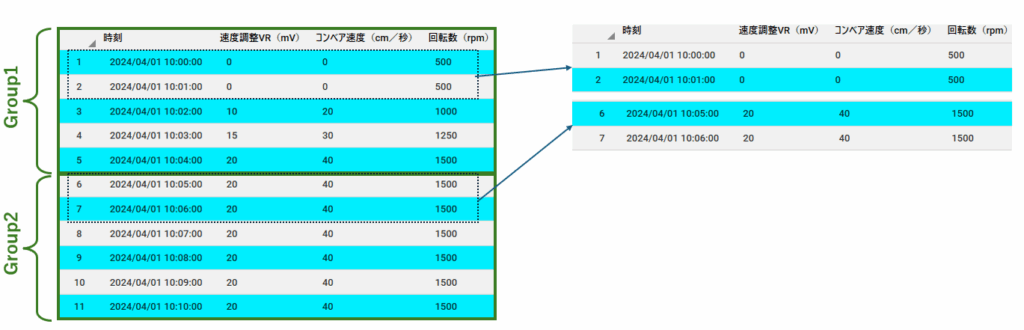
大量データの中に時間帯やカテゴリの偏りがある場合、ストラティファイドサンプリング(層化抽出)が有効です。
これは、データをあらかじめ「層(stratum)」でグループ分けを行い、それぞれの層から均等にサンプルを抽出する手法です。
たとえば、1日分のセンサーデータを1時間ごとにグルーピングし、各グループ(各時間帯)から同数のデータを抽出すれば、時間的な偏りを抑えた代表サンプルが得られます。
- 例:夜間はセンサーの動きが少なく、昼間は活発な場合でも、各時間帯から均等に抽出すれば、全体の傾向をバランスよく反映できる
- 例:複数の装置やユーザーからのデータを扱う場合、装置ごとに層を分けて抽出すれば、特定の装置に偏らない代表サンプルが得られる
この手法は、時系列の流れやカテゴリ間の比較を行いたい場合に特に有効です。
ただし、以下のような注意点があります。
- 層の設計が必要(例:時間帯、装置ID、ユーザーIDなど)
- 実装がやや複雑で、事前に層の分布を把握しておく必要がある
- 層内のデータ量が少ない場合、サンプル数が制限されることがある
ストラティファイドサンプリングを使うべきなのは、次のようなケースです
- 時系列の変化や周期性を含めて、全体の傾向をバランスよく捉えたい
- 複数のカテゴリ(装置・ユーザー・地域など)を比較したい
- 単純なランダムサンプリングでは偏りが気になる
このような場合において、ストラティファイドサンプリングは、最も信頼性の高い代表抽出手法のひとつです。
特に、「傾向も分布も両方見たい」というニーズに対して、実務的に非常に強力な選択肢となります。
目的特化型の抽出手法
これまで紹介してきた「先頭区間抽出」「間引き」「無作為抽出」「層化抽出」は、いずれもデータ全体の傾向や分布を、できるだけ損なわずに軽量化するための汎用的なサンプリング手法でした。
これから紹介する手法は、データ量の規模に関係なく、特定の分析目的(何を見たいか)に応じて意味のある特徴を抽出するための設計手法です。
これらは汎用的なサンプリングとは異なり、目的外には使えませんし、サンプリング済みのデータでは正しい結果が得られない可能性があります。そのため、生データに対して直接適用することが前提となります。
以下が、その代表的な手法です。
| 手法名 | 方法の概要 | 主な目的 | メリット | 注意点・取りこぼしリスク |
|---|---|---|---|---|
| 統計サマリ | 平均・中央値・分散などの統計量を算出 | 中央傾向やばらつきの把握 | 軽量・高速に全体傾向を要約できる | 局所的な変化や異常は見えにくい |
| ピーク抽出 | 極値や急変動を検出して抽出 | 異常値・急変動の補足 | サマリでは消える重要な局所情報を保持 | 平常時の傾向は見えにくい可能性あり |
| 分布裾抽出(分位点ベース) | 5%・95%などの分位点を基準に抽出 | 分布の広がり・外れ値の把握 | 分布の端を明示的に捉えられる | 中央傾向の代表性は低くなる可能性あり |
統計サマリ抽出(Aggregated statistics)
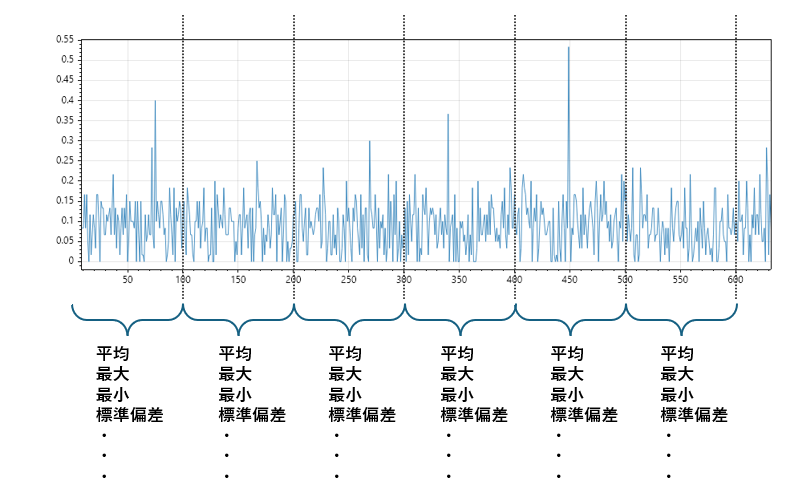
統計サマリ抽出とは、一定の時間ブロックやカテゴリ単位で、平均・最大・最小・標準偏差などの統計値を計算する手法です。
これにより、元のデータの傾向や変動を保持したまま、メモリに載るサイズに圧縮された“意味あるデータ”を得ることができます。
たとえば、1ms間隔で記録されたセンサーデータがあるとします。1分間で約60,000行のデータが生成される計算です。
このままでは描画も分析も困難ですが、以下のように集約すれば、1分につき1行の“意味あるサマリ”が得られます。
このようなサマリは、折れ線グラフやヒートマップで傾向を可視化するのに最適です。
可視化を前提に統計サマリ抽出で押さえておきたい項目として、以下のものがあります。
| 指標 | 用途 |
|---|---|
| 平均(mean) | 傾向の中心。折れ線グラフの主線に使える |
| 最大(min) / 最小(max) | 範囲の帯やピーク検出に使える |
| 四分位数(Q1 / Q2 / Q3) | 分布の形。箱ひげ図やヒストグラムの補助に使える |
| 件数(count) | 欠損率や密度補正に使える |
| 標準偏差(stddev) | 変動の大きさ。安定性の指標として便利 |
ピーク抽出
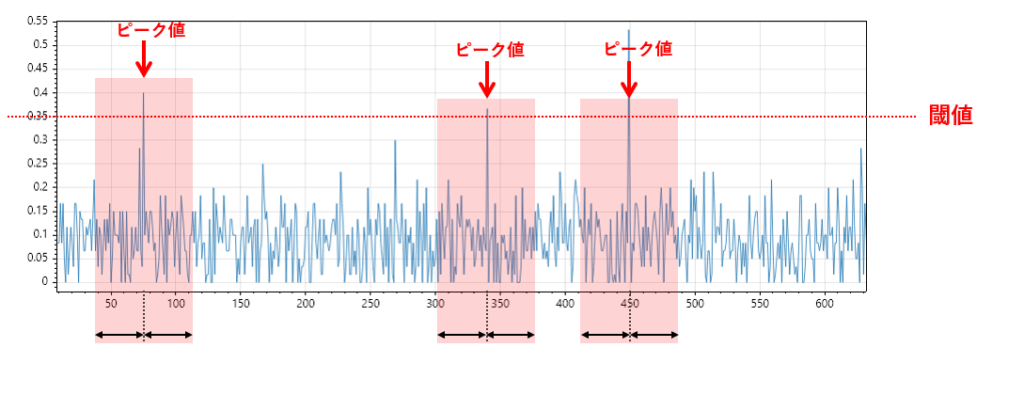
大量データの中から異常や急変動を捉えたい場合、ピーク抽出(極値検出)は非常に有効な手法です。
これは、センサーデータの中で急激な変化やスパイクが発生している箇所を検出し、その周辺データを抽出することで、通常のサマリでは見逃されがちな重要な局所情報を可視化することを目的とします。
たとえば、scipy.signal.find_peaks() を使えば、一定の高さや間隔を条件にしてスパイクを検出できます。
そのピーク位置を中心に前後数件のデータを抽出すれば、異常の発生タイミングやその前後の挙動を俯瞰することが可能です。
- 例:センサーが異常振動を起こした瞬間の波形を抽出して、異常の兆候を可視化
- 例:急激な温度上昇や電流スパイクを検出し、装置の異常動作を分析
この手法は、平均値や分散などの統計サマリでは埋もれてしまう局所的な異常を捉えるのに特化しています。
ただし、以下のような注意点があります。
- 平常時の傾向や全体分布は見えにくい
- ピーク検出のパラメータ(高さ・距離・幅など)によって結果が大きく変わる
- ノイズが多い場合、誤検出が増える可能性がある
ピーク抽出を使うべきなのは、次のようなケースです。
- 異常検知やスパイクの発生タイミングを重点的に分析したい
- 通常のサマリでは見えない局所的な変化を可視化したい
- 異常の前後の挙動を含めて、原因分析や予兆検出を行いたい
このような場合において、ピーク抽出は“軽量かつ高密度な異常情報”を得るための強力な手段です。
他のサンプリング手法と組み合わせることで、傾向と異常の両方を俯瞰する可視化が可能になります。
分布裾抽出(分位点ベース)
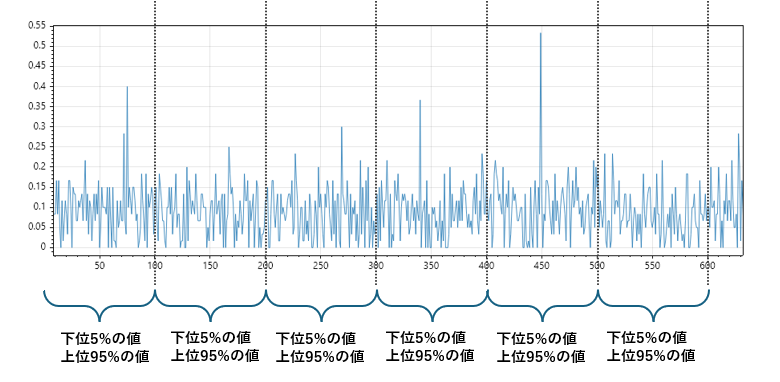
大量データの中で、分布の広がりや外れ値の傾向を把握したい場合に有効なのが「分布裾抽出(分位点ベース)」です。
これは、データの上下端(裾)に位置する値を抽出することで、分布の広がり・偏り・異常値の存在を可視化することを目的とした手法です。
たとえば、全体の5%点(下位5%)と95%点(上位5%)を抽出すれば、中央値では見えない分布の端の特徴を捉えることができます。
- 例:温度センサーのデータで、通常は20〜30℃だが、極端に高い・低い値が混在している場合、それらを抽出して異常傾向を確認できる
- 例:ユーザー行動ログで、極端に短い・長い滞在時間を抽出して、異常行動や特殊パターンを分析できる
この手法は、平均や中央値では埋もれてしまう“分布の裾”に注目することで、全体の広がりや異常の兆候を把握するのに適しています。
ただし、以下のような注意点があります。
- 中央傾向(平均・中央値)を代表する目的には不向き
- 外れ値が多い場合、抽出結果がノイズに近くなる可能性がある
- 分位点の設定(5%・10%・25%など)によって抽出範囲が大きく変わる
分布裾抽出を使うべきなのは、次のようなケースです。
- 分布の広がりや偏りを視覚的に把握したい
- 外れ値や極端値の傾向を分析したい
- 通常の統計サマリでは見えない“端の情報”に注目したい
このような場合において、分布裾抽出は“分布の形を立体的に捉える”ための有効な手段です。
他のサンプリング手法と組み合わせることで、傾向・分布・異常の三要素をバランスよく可視化できます。
SQLiteによる大量データの軽量化

大量データを軽量化する際には、元のCSVファイルを直接扱う方法と、軽量なデータベース(SQLite)を活用する方法の2通りがあります。
CSVファイルをそのまま扱う場合、メモリ不足を避けるためにチャンク(分割)読み込み+逐次処理が基本となります。
しかし、層化抽出・統計サマリ・ピーク抽出など、グルーピングを伴う処理では、チャンク単位では正しい結果が得られないことがあります。
- 分布全体が見えないと、四分位数や標準偏差が正しく計算できない
→ チャンク単位では「どこが端か」が分からず、統計値がズレる - チャンクをまたいだ統合処理が複雑でバグの温床になりやすい
→ 前後のチャンクをつなぐ処理が必要になるが、実装が煩雑 - 結局すべてのチャンクを結合するなら、メモリオーバーのリスクがある
→ 巨大ファイルでは全件読み込みが現実的でなくなる - 統計計算のためにチャンクごとの結果を管理する必要が生じる
→プログラムが複雑化し、処理速度も著しく低下する
このような理由から、本記事では軽量かつ柔軟に集約処理が可能なSQLiteの活用を推奨します。
SQLiteを使えば、グルーピング・統計計算・抽出処理を安定して行えるだけでなく、メモリ制約を気にせずに設計できるという利点があります。
SQLiteとは
SQLiteは、Python標準ライブラリに含まれている軽量な組み込み型データベースです。
そのため、インストール不要で、環境構築の手間がほぼゼロ。すぐに使い始めることができます。
実務で扱う大量データに対して、以下のような利点があります。
- 時間ブロック単位の集約が GROUP BY で簡単に書ける
→ 例:GROUP BY strftime('%Y-%m-%d %H:%M', timestamp)で1分ごとの統計が簡潔に記述可能 - WHERE句やインデックスで高速に絞り込みができる
→ 期間指定やセンサーIDによるフィルタが高速に実行でき、傾向把握や異常検知に役立つ - メモリに載せずに処理可能なため、巨大データでも安定
→ 数千万件のデータでも、オンディスク処理によりメモリオーバーせずに統計抽出が可能 - 必要に応じて、分位点やヒストグラムの近似処理も拡張できる
→ 外部関数や仮想テーブルを使えば、分布の形状把握や特徴量抽出にも対応できる
実務では「CSVよりも柔軟に集約したい」「メモリに載らないデータを扱いたい」といった場面で、SQLiteが非常に有効です。
SQLiteに関する詳しい説明は、下記の記事をご覧ください。
【基礎編】SQLiteの基本操作をPythonで簡単に!初めてのデータベース入門
【応用編】SQLiteのメタデータをPythonで利用しよう!初めてのデータベース入門
【実用編】 pandas×SQLiteでCSVをデータベースで管理しよう!
先頭区間抽出
このSQLは、sampleテーブルから value が欠損していないレコードを対象に、時刻順に並べた上で、先頭から1000万件を抽出する処理です。
SELECT *
FROM sample
WHERE value IS NOT NULL
ORDER BY timestamp ASC
LIMIT 10000000;単純間引きのサンプル
このSQLは、timestamp列を使ってデータを1時間ごとに区切り、各時間帯の中で最も早いレコード(先頭の1件)を抽出する処理です。ROW_NUMBER() ウィンドウ関数を使って、各1時間のグループ内で時刻順に番号を振り、rn = 1 によって先頭のレコードだけを選択しています。
WITH ranked AS (
SELECT *,
ROW_NUMBER() OVER (
PARTITION BY strftime('%Y-%m-%d %H:00:00', timestamp)
ORDER BY timestamp ASC
) AS rn
FROM data
)
SELECT *
FROM ranked
WHERE rn = 1
ORDER BY timestamp;無作為抽出(ランダムサンプリング)
このSQLは、timestamp列を使ってデータを1時間ごとに区切り、各時間帯の中からランダムに1件だけレコードを抽出します。ROW_NUMBER()ウィンドウ関数と ORDER BY RANDOM() を組み合わせることで、時間帯ごとの代表値をランダムに選ぶ処理を実現しています。
WITH randomized AS (
SELECT *,
ROW_NUMBER() OVER (
PARTITION BY strftime('%Y-%m-%d %H:00:00', timestamp)
ORDER BY RANDOM()
) AS rn
FROM data
)
SELECT *
FROM randomized
WHERE rn = 1層化抽出(ストラティファイドサンプリング)
このSQLは、timestamp列を使ってデータを1時間ごとにグループ化し、各時間帯からランダムに3件ずつレコードを抽出する処理です。ROW_NUMBER() ウィンドウ関数と ORDER BY RANDOM() を組み合わせることで、各時間帯の中でランダムな順番を付け、先頭3件を選び出す層化抽出を実現しています。
WITH stratified AS (
SELECT *,
ROW_NUMBER() OVER (
PARTITION BY strftime('%Y-%m-%d %H:00:00', timestamp)
ORDER BY RANDOM()
) AS rn
FROM data
)
SELECT *
FROM stratified
WHERE rn <= 3統計サマリ抽出のサンプル
このSQLは、時刻列を5分単位で区切った時間帯ごとにデータを集計し、各時間帯における 速度調整VR(mV) の件数・平均・最小値・最大値を算出します。strftime と printf を組み合わせて、時刻を「○時○分(5分刻み)」に丸めた上でグルーピングしています。
たとえば「13:07」は「13:05」に、「13:12」は「13:10」に丸められ、同じ5分間に属するデータとして集計されます。
SELECT
strftime('%Y-%m-%d %H:', 時刻) ||
printf('%02d', CAST(strftime('%M', 時刻) AS INTEGER) / 5 * 5) AS 時刻5分単位,
COUNT(速度調整VR(mV)) AS 件数,
AVG(速度調整VR(mV)) AS 平均,
MIN(速度調整VR(mV)) AS 最小,
MAX(速度調整VR(mV)) AS 最大
FROM sample
GROUP BY 時刻5分単位
ORDER BY 時刻5分単位ピーク抽出(局所最大値)
このSQLは、timestamp順に並べたデータに対して、前後の値と比較して局所的に最大となるピーク値を抽出する処理です。LAG / LEAD 関数を使って前後の値を取得し、中央の値が両隣より大きい場合にピークと判定します。
WITH with_neighbors AS (
SELECT
timestamp,
target_column,
LAG(target_column, 1) OVER (ORDER BY timestamp) AS prev_value,
LEAD(target_column, 1) OVER (ORDER BY timestamp) AS next_value
FROM data
)
SELECT timestamp, target_column
FROM with_neighbors
WHERE target_column > prev_value AND target_column > next_value;このSQLは、timestamp順に並べたデータに対して、局所的なピーク値を抽出する処理です。LAG と LEAD 関数を使って、各レコードの前後の値を取得し、中央の値が両隣より大きい場合にピークと判定します。
さらに、value >= 100 の条件を加えることで、一定のしきい値を超えたピークのみを抽出しています。
WITH with_neighbors AS (
SELECT
timestamp,
value,
LAG(value) OVER (ORDER BY timestamp) AS prev_value,
LEAD(value) OVER (ORDER BY timestamp) AS next_value
FROM data
)
SELECT timestamp, value
FROM with_neighbors
WHERE value > prev_value
AND value > next_value
AND value >= 100; -- ← しきい値を追加分布裾抽出(分位点ベース)
このSQLは、value列の値に基づいてデータを100分位(パーセンタイル)に分割し、その中から下位5%と上位5%の極端な値(裾)を抽出する処理です。NTILE(100) ウィンドウ関数を使って、valueの昇順で全体を100等分し、各レコードに分位番号(1〜100)を割り当てています。percentile <= 5 は下位5%(分布の左裾)、percentile >= 96 は上位5%(分布の右裾)に相当します。
WITH ranked AS (
SELECT *,
NTILE(100) OVER (ORDER BY value) AS percentile
FROM data
)
SELECT *
FROM ranked
WHERE percentile <= 5 OR percentile >= 96統計サマリ抽出の可視化手法
軽量化済みのデータであれば、各時間ブロックの代表レコードをそのまま可視化できるため、特別な工夫は不要です。
一方で、統計サマリを用いる場合は、すでに複数の値が平均や最大・最小などで要約されているため、そのまま折れ線グラフにしても実データの分布や変動が見えにくくなることがあります。
データの推移と変動を見る(fig1)
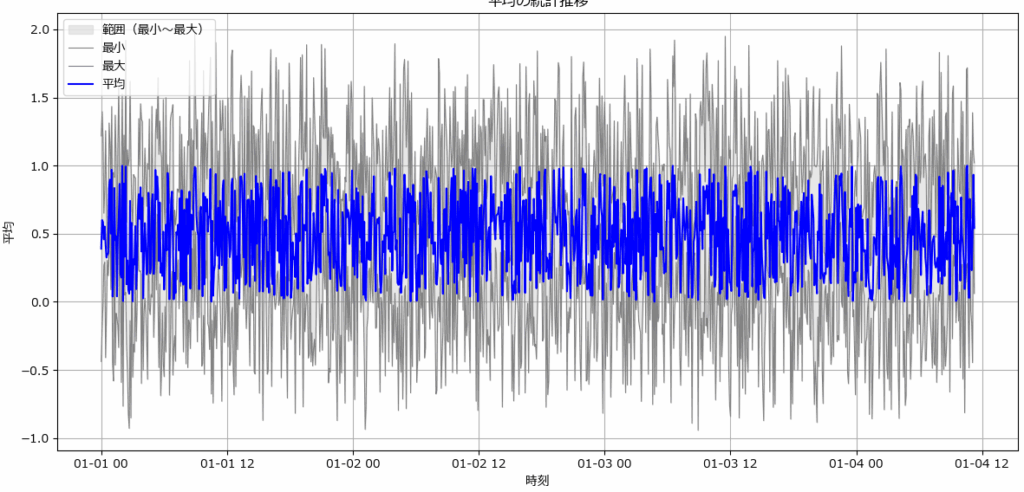
データの推移と変動を見るには、平均・最大・最小を組み合わせた可視化が有効です。
具体的には、平均値を折れ線で描画しつつ、最大値と最小値の間を塗りつぶすことで、データの中心的な傾向(平均の推移)と、ばらつきの大きさ(変動幅)を同時に把握できます。
データの偏り/外れ値の影響をみる(fig2)
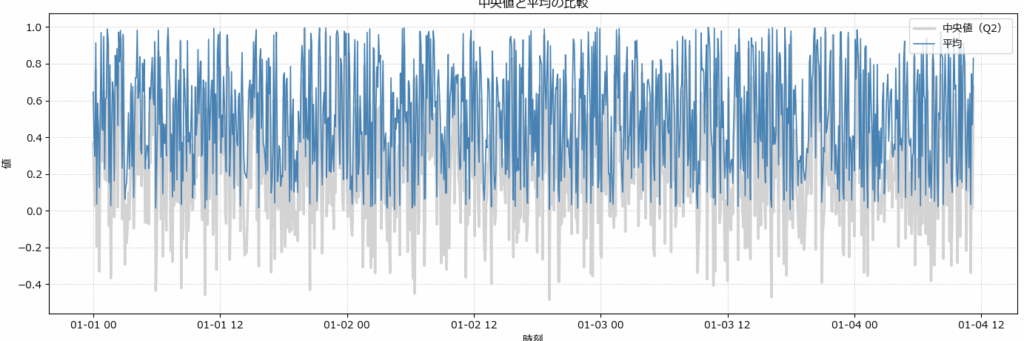
平均と中央値を比較することで、データの「偏り」や「外れ値の影響」が明確に見えるようになります。特にサマリ統計を使った傾向把握では、両者の差が分布の歪みや実態とのズレを示す重要な手がかりになります。
| 指標 | 定義 | 特性 | 向いている用途 |
|---|---|---|---|
| 平均 | 全データの合計 ÷ 件数 | 外れ値に影響されやすい | KPI、売上、クリック率など |
| 中央値 | 昇順に並べた中央の値 | 外れ値に強く、分布の中心を安定的に示す | 滞在時間、年収、満足度などばらつきが大きい指標 |
分布の安定性と外れ値の影響を見る(fig3)
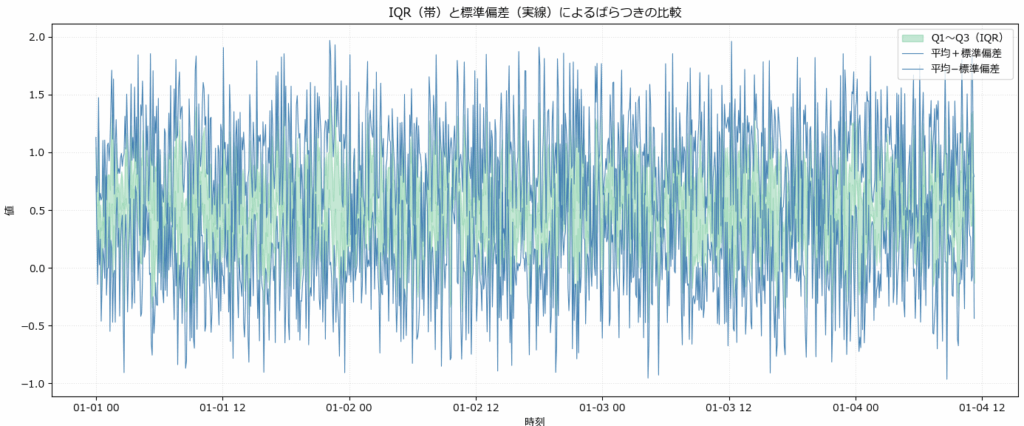
データのばらつきを可視化する方法として、IQR(四分位範囲)と標準偏差はよく使われます。両者を帯として並べて表示することで、分布の構造や外れ値の影響を直感的に把握できます。
| 指標 | 定義 | 特性 | 向いている用途 |
|---|---|---|---|
| IQR(Q1〜Q3) | 第1四分位〜第3四分位の範囲 | 外れ値に強く、分布の中心を安定的に示す | 安定性の評価、中央値ベースの分布把握 |
| 標準偏差 | 平均からのばらつきの平均距離 | 外れ値に敏感で、全体のばらつきを示す | 異常検知、正規分布前提のばらつき評価 |
ピーク抽出(局所最大値)の可視化手法
ピーク抽出(局所最大値)の可視化では、単にピークを描くことが目的ではなく、ピークの「意味」「構造」「分布」を読み解くことが主眼です。
| 観点 | 見るべき内容 | 目的・意味 |
|---|---|---|
| ピークの位置 | 時系列上のどこでピークが出現しているか | イベントのタイミングや周期性の把握 |
| ピークの強度 | ピークの高さ(値) | 重要度の判定、しきい値との関係 |
| ピークの間隔 | ピーク同士の時間的距離 | 周期性・連続性・異常の検出 |
| ピークの形状 | 鋭さ・幅・持続時間 | スパイク型か山型か、急変か緩やかな変動か |
| ピークの密度 | 一定期間内のピーク数 | 活動量・異常集中・イベント頻度の把握 |
| 抽出妥当性 | 折れ線の山頂とピーク点の一致 | 抽出ロジックの正当性の検証 |
| ピークの前後傾向 | ピーク前後の値の変化 | 前兆や余波の検出、異常の兆しの把握 |
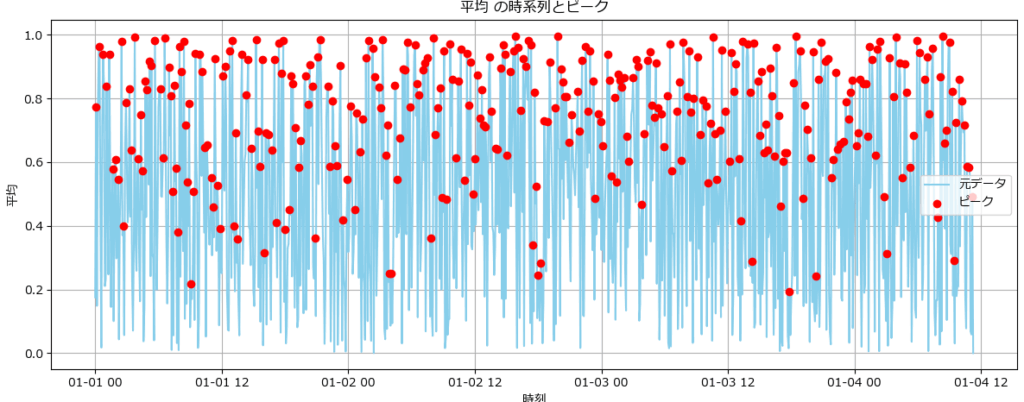
平均値の変動とピークを確認する(fig4)
このグラフは、時系列データにおける「平均値の変動」と、その中で検出されたピーク点を可視化したものです。
分布裾抽出の可視化手法
分布裾抽出(分位点ベース)では、データの「端(裾)」に位置する極端な値がどんな特徴を持っているかを分析することが目的です。
| 観点 | 見るべき内容 | 目的・意味 |
|---|---|---|
| 値の極端さ | 上位・下位の分位点に位置する値の大きさ | 外れ値・異常値の検出、しきい値設定の参考 |
| 分布の偏り | 裾にどれだけデータが集中しているか | 偏った分布か、均等か、歪みの把握 |
| 裾の形状 | 裾が急峻か緩やかか | 分布の広がり、リスクや異常の兆候の把握 |
| 裾の時系列分布 | 極端値がいつ発生しているか | 異常の発生タイミング、イベントとの関連 |
| 裾の頻度 | 裾に該当するデータの件数 | 極端値の多さ、異常の頻度や濃度の把握 |
| 裾の変化傾向 | 時間とともに裾の位置が変化しているか | 分布の動的変化、トレンドや異常の進行 |
| 他指標との関係 | 裾のとき他の列に変化があるか | 多変量的な異常検知、因果関係の探索 |
箱ひげ・ヒストグラム・散布図(fig5)
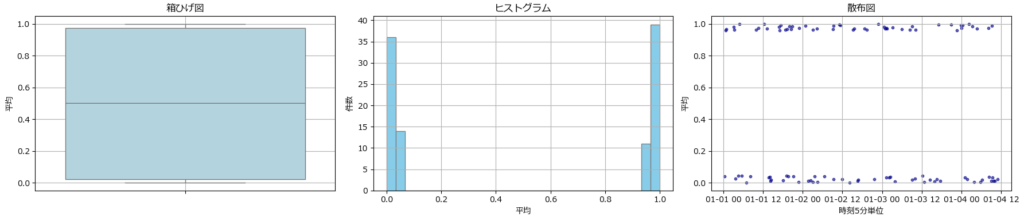
分布裾抽出は、箱ひげ図、ヒストグラム、散布図を使って両端の状態を確認します。
| グラフ | 役割 | 見るべきポイント |
|---|---|---|
| 箱ひげ図 | 分位点と外れ値の構造を可視化 | 裾の広がり、外れ値の有無、中央値の偏り |
| ヒストグラム | 分布の密度と偏りを可視化 | 裾にどれだけデータが集中しているか、歪みの有無 |
| 散布図 | 時系列的な裾の出現を可視化 | 極端値がいつ発生しているか、周期性や集中の有無 |
本記事で使用したサンプルコード集
サンプルデータの生成プログラム
import pandas as pd
import numpy as np
# 件数
n = 1000
# ランダムな平均値(0〜1)
mean_values = np.random.rand(n)
# ランダムな幅(0〜1)
delta = np.random.rand(n)
# 最大・最小値を計算
max_values = mean_values + delta
min_values = mean_values - delta
# 標準偏差(最大・最小からの距離の平均)
std_values = ((max_values - mean_values) + (mean_values - min_values)) / 2
# 四分位数(Q1 = 平均 - 0.5 * delta, Q3 = 平均 + 0.5 * delta と仮定)
q1_values = mean_values - 0.5 * delta
q3_values = mean_values + 0.5 * delta
# 中央値(Q2)を平均より少し低い
q2_values = mean_values - np.random.rand(n) * 0.05
# 時刻(5分間隔で生成)
start_time = pd.Timestamp('2025-01-01 00:00')
time_values = [start_time + pd.Timedelta(minutes=5 * i) for i in range(n)]
# DataFrame化
df = pd.DataFrame({
'時刻5分単位': time_values,
'平均': mean_values,
'最大': max_values,
'最小': min_values,
'標準偏差': std_values,
'Q1': q1_values,
'Q3': q3_values,
'Q2': q2_values
})
# 表示(先頭5件)
print(df.head())fig1の描画プログラム
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
def plot_stats(df, time_col, mean_col, min_col, max_col):
"""
集計済みのDataFrameから、指定された列を使って統計グラフを描画する関数。
最大・最小の範囲を塗りつぶし、平均は塗りつぶさず折れ線のみ(マーカーなし)。
Parameters:
- df: pandas.DataFrame(すでに集計済み)
- time_col: str(時刻列名)
- mean_col: str(平均列名)
- min_col: str(最小列名)
- max_col: str(最大列名)
"""
# 時刻列をdatetime型に変換(必要なら)
if not pd.api.types.is_datetime64_any_dtype(df[time_col]):
df[time_col] = pd.to_datetime(df[time_col])
# グラフ描画
plt.figure(figsize=(12, 6))
# 最大・最小の範囲を塗りつぶし(薄いグレー)
plt.fill_between(df[time_col], df[min_col], df[max_col], color='lightgray', alpha=0.5, label='範囲(最小〜最大)')
# 最大・最小の線(細いグレーの実線)
plt.plot(df[time_col], df[min_col], color='gray', linewidth=0.8, label='最小')
plt.plot(df[time_col], df[max_col], color='gray', linewidth=0.8, label='最大')
# 平均(マーカーなしの青い折れ線)
plt.plot(df[time_col], df[mean_col], label='平均', color='blue', linewidth=1.5)
plt.xlabel('時刻')
plt.ylabel(mean_col)
plt.title(f'{mean_col}の統計推移')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()fig2の描画プログラム
import matplotlib.pyplot as plt
from matplotlib import rcParams
def plot_median_vs_mean(df,
time_col='時刻5分単位',
mean_col='平均',
q2_col='Q2'):
rcParams['font.family'] = 'Meiryo'
if not pd.api.types.is_datetime64_any_dtype(df[time_col]):
df[time_col] = pd.to_datetime(df[time_col])
x = df[time_col]
plt.figure(figsize=(14, 5))
# 中央値(Q2):太めの薄グレー
plt.plot(x, df[q2_col], color='lightgray', linewidth=2.5, label='中央値(Q2)')
# 平均:細めの青系(steelblue)
plt.plot(x, df[mean_col], color='steelblue', linewidth=1.2, label='平均')
plt.xlabel('時刻')
plt.ylabel('値')
plt.title('中央値と平均の比較')
plt.legend(loc='upper right')
plt.grid(True, linestyle=':', alpha=0.8)
plt.tight_layout()
plt.show()fig3の描画プログラム
import matplotlib.pyplot as plt
from matplotlib import rcParams
def plot_iqr_and_std_lines(df,
time_col='時刻5分単位',
mean_col='平均',
std_col='標準偏差',
q1_col='Q1',
q3_col='Q3'):
rcParams['font.family'] = 'Meiryo'
if not pd.api.types.is_datetime64_any_dtype(df[time_col]):
df[time_col] = pd.to_datetime(df[time_col])
x = df[time_col]
plt.figure(figsize=(14, 6))
# IQR帯(Q1〜Q3):薄緑
plt.fill_between(x, df[q1_col], df[q3_col],
color='mediumseagreen', alpha=0.3, label='Q1〜Q3(IQR)')
# 標準偏差の上限・下限を細い実線で描画(青)
plt.plot(x, df[mean_col] + df[std_col], color='steelblue', linewidth=0.8, linestyle='-', label='平均+標準偏差')
plt.plot(x, df[mean_col] - df[std_col], color='steelblue', linewidth=0.8, linestyle='-', label='平均−標準偏差')
plt.xlabel('時刻')
plt.ylabel('値')
plt.title('IQR(帯)と標準偏差(実線)によるばらつきの比較')
plt.legend(loc='upper right')
plt.grid(True, linestyle=':', alpha=0.4)
plt.tight_layout()
plt.show()
fig4の描画プログラム
指定したDataFrameとカラムに対して、自動でピークを検出する関数。
def extract_peaks(df, column):
"""
指定列に対して局所ピーク(前後より大きい値)を抽出する。
Parameters:
df (pd.DataFrame): 時系列データを含むDataFrame
column (str): ピーク抽出対象の列名(数値列)
Returns:
pd.DataFrame: ピーク時刻と値を含むDataFrame
"""
df = df.copy()
df['prev'] = df[column].shift(1)
df['next'] = df[column].shift(-1)
peaks = df[(df[column] > df['prev']) & (df[column] > df['next'])]
return peaks[[df.columns[0], column]] # 時刻列と対象列のみ返す折れ線にピークを重ね合わせる関数
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
def plot_with_peaks(df, column, peaks):
"""
指定列の折れ線グラフにピーク点を重ねて描画する。
Parameters:
df (pd.DataFrame): 元の時系列データ
column (str): 描画対象の列名
peaks (pd.DataFrame): extract_peaksで得られたピーク点のDataFrame
"""
time_col = df.columns[0] # 時刻列(先頭列)を自動取得
plt.figure(figsize=(12, 5))
plt.plot(df[time_col], df[column], label='元データ', color='skyblue')
plt.scatter(peaks[time_col], peaks[column], color='red', label='ピーク', zorder=5)
plt.xlabel('時刻')
plt.ylabel(column)
plt.title(f'{column} の時系列とピーク')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
fig5の描画プログラム
指定列の上下分位点に基づいて裾(極端値)を抽出する関数
def extract_tail(df, column, lower_q=0.05, upper_q=0.95):
"""
指定列の上下分位点に基づいて裾(極端値)を抽出する。
Parameters:
df (pd.DataFrame): データフレーム
column (str): 対象の数値列
lower_q (float): 下位分位点(例:0.05)
upper_q (float): 上位分位点(例:0.95)
Returns:
pd.DataFrame: 裾に該当する行のみ抽出したDataFrame
"""
lower = df[column].quantile(lower_q)
upper = df[column].quantile(upper_q)
return df[(df[column] <= lower) | (df[column] >= upper)]import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
import matplotlib.pyplot as plt
import seaborn as sns
def plot_distribution_summary(df, column, time_column):
"""
指定列の箱ひげ図・ヒストグラム・散布図を横並びで描画する。
Parameters:
df (pd.DataFrame): データフレーム
column (str): 分布対象の数値列
time_column (str): 散布図のX軸に使う時刻列
"""
fig, axes = plt.subplots(1, 3, figsize=(18, 4))
# 箱ひげ図
sns.boxplot(y=df[column], ax=axes[0], color='lightblue')
axes[0].set_title('箱ひげ図')
axes[0].grid(True)
# ヒストグラム
axes[1].hist(df[column], bins=30, color='skyblue', edgecolor='gray')
axes[1].set_title('ヒストグラム')
axes[1].set_xlabel(column)
axes[1].set_ylabel('件数')
axes[1].grid(True)
# 散布図
axes[2].scatter(df[time_column], df[column], s=10, color='darkblue', alpha=0.6)
axes[2].set_title('散布図')
axes[2].set_xlabel(time_column)
axes[2].set_ylabel(column)
axes[2].grid(True)
plt.tight_layout()
plt.show()
まとめ
何億行にも及ぶ時系列データをそのまま扱うのは現実的ではなく、軽量化と目的に応じた抽出・可視化の工夫が不可欠です。
本記事では、以下の3つの柱に沿って、実務で役立つ設計手法を体系的に紹介しました:
- 汎用サンプリング:先頭抽出・間引き・ランダム・層化により、分布の代表性を保ちつつ軽量化
- 目的特化型抽出:統計サマリ・ピーク検出・分布裾抽出で、傾向や異常を的確に捉える
- SQLite活用:巨大データでも安定した集約・抽出が可能。Pythonとの連携で柔軟な設計が実現
さらに、平均・中央値・IQR・標準偏差などの統計指標を活かした可視化手法と、具体的なサンプルプログラムも紹介しました。
メモリに載らない規模のデータを扱う場面で、この記事が役立てば幸いです。




コメント