Local Outlier Factor(LOF)は、機械学習における異常検知手法の一つで、特に複雑なデータ分布の中から局所的に異常なデータポイントを検出できることで注目されています。
このアルゴリズムは、データの「局所的な密度」を基に異常を判定するユニークなアプローチを取っています。周囲のデータ点と比較してどれだけ孤立しているかを数値化することで、従来の距離ベース手法では見逃されやすい異常を見つけることが可能です。
製造業においても、LOFは品質管理や設備保全における異常検知の手段として活用されており、センサー群の中で局所的に浮いた値や異常挙動を早期に発見することができます。これにより、異常の兆候を見逃さず、予防保全や品質向上につなげることが可能です。
この記事では、LOFの概要から製造業での応用、具体的な実装方法まで、詳しく解説します。
Local Outlier Factor(LOF)とは?
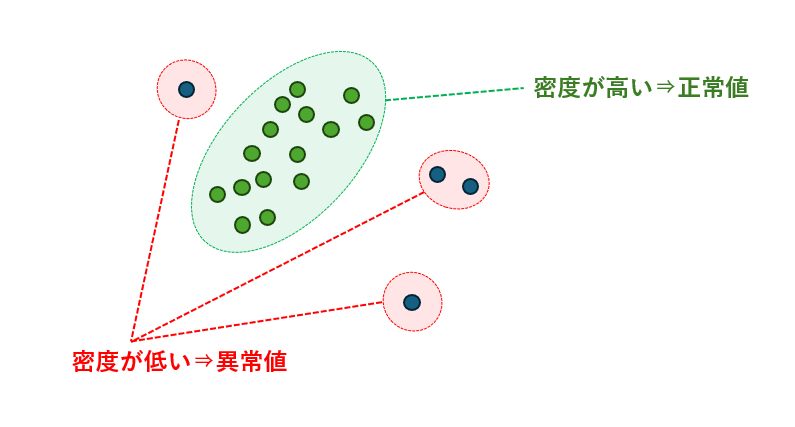
Local Outlier Factor(LOF)は、異常検知のためのアルゴリズムであり、データの局所的な密度を利用して異常を特定します。
LOFは各データポイントの周囲に存在する近傍点との距離を評価し、その点がどれだけ周囲と比べて孤立しているかを数値化します。局所的な密度が周囲より低い点は「浮いている」と判断され、外れ値として検出されます。
一般的に、異常なデータポイントは少数派であり、周囲の点と比べて密度が低いため、LOFスコアが高くなり異常として識別されます。
LOFは各点の異常度を周囲の学習データとの相対比較で算出するため、全ての学習データをモデル内に保持する必要があります。このため、Isolation Forest や One-Class SVMのようにモデルを固定して再利用する使い方には向いていません。
Isolation Forest や One-Class SVM は、学習時にデータ全体のパターンをモデルとして記憶するため、学習済みモデルを保存して新しいデータに対してもそのまま異常検知が可能です。一方、LOF(Local Outlier Factor)は各データ点の局所密度を周囲の学習データと比較して異常度を算出する手法のため、学習データなしでは新しいデータの異常度を評価できません。
メリット
- 局所性を考慮:クラスタごとに密度が異なる場合でも、局所的な異常を検出できる。
- 柔軟性:データ分布の仮定を必要とせず、非線形な構造にも対応可能。
- 解釈性:LOFスコアを用いて「どの程度周囲から浮いているか」を定量的に説明できる。
- 多用途性:センサーデータ、ネットワークログ、金融データなど幅広い分野で利用可能。
デメリット
- パラメータ依存:近傍数 k の選び方に結果が大きく左右される。
- 計算コスト:距離計算が多いため、大規模データでは処理時間が増える。
- 高次元データに弱い:次元が増えると距離の意味が薄れ、精度が低下する可能性がある。
LOFに適したデータ
OFは、局所的に密度が低い少数派のデータを検出するのに適しています。
- 製造業のセンサーデータにおいて、特定の時刻だけ異常値が出るケース
- ネットワークトラフィックの中で、特定の通信だけ異常に孤立しているケース
- 金融業界での不正検知において、通常の取引群から局所的に浮いた取引
このように、LOFは「周囲との関係性」を重視するため、局所的な異常が重要なケースで効果的に機能します。
LOFの製造業における用途
LOFは「局所的な密度の違い」に着目して異常を検知するアルゴリズムです。製造業の現場では、センサーや工程データが複雑に絡み合い、単純な閾値判定では見逃される異常が多く存在します。LOFはそのような「周囲から浮いたデータ」を見つけるのに強みを発揮します。
- 設備の微細な異常検知
振動や温度センサーのデータを継続的に監視することで、通常の動作群から局所的に外れた挙動を検出することができます。こうした分析によって、大きな故障の前に現れる「小さな異常サイン」を早期に捉え、予防保全へとつなげることが可能になります。 - 製品品質のばらつき検出
製造ラインで得られる寸法や重量などの測定値を分析すると、全体的には正常範囲に収まっていても、局所的に密度が低い「浮いた製品」が存在する場合があります。LOFを用いることでそのような製品を検出し、不良品の流出を未然に防止することができます。 - プロセス条件の逸脱監視
温度や圧力、流量といった工程パラメータをリアルタイムで監視することで、通常の運転条件から局所的に外れた値を検出できます。これにより工程の安定性を維持し、製造プロセス全体の信頼性を高めることができます。 - サプライチェーンの異常挙動
在庫や物流データを分析すると、局所的に異常な供給遅延や過剰在庫が検出されることがあります。こうした異常を早期に把握することで、サプライチェーン全体の効率化やリスク低減に貢献することができます。 - エネルギー効率の改善
設備の電力消費や稼働データを分析することで、通常のパターンから局所的に外れた消費を検出できます。これにより、無駄なエネルギー使用を特定し、コスト削減や効率改善につなげることが可能です。
LOFの実装方法
モジュールのインストール
LOFを実装するには、Pythonとscikit-learnライブラリが必要です。以下のコマンドで必要なライブラリをインストールできます。
pip install scikit-learn numpy pandas
学習と異常検知
- このサンプルプログラムでは、①学習データ生成 ②LOFによる判定 ③テストデータ投入 ④結果出力という一連の処理を行っています。
- 実データは正規分布ではない場合が多いため、学習データは複数の分布を混在させています。LOFは局所的な密度を比較するため、クラスタが複数存在しても異常を検出できます。
import numpy as np
from sklearn.neighbors import LocalOutlierFactor
# 学習データ(100個の値を持つ2次元の正常データ)の作成
np.random.seed(42)
X_train = 0.3 * np.random.randn(100, 2)
X_train = np.r_[X_train + 2, X_train - 2, X_train]
# LOFモデルの作成と学習+判定
# n_neighborsは近傍点の数、contaminationは異常の割合を推定
lof = LocalOutlierFactor(n_neighbors=20, contamination=0.05)
y_pred_train = lof.fit_predict(X_train)
print("正常データの判定結果:", y_pred_train.tolist())
# テストデータを生成(異常と判定されるよう、振幅を-4~4で生成)
X_test = np.random.uniform(low=-4, high=4, size=(20, 2))
# LOFは新しいデータに対してpredictを直接使えないため、再度fit_predictを実行
y_pred_test = lof.fit_predict(np.r_[X_train, X_test])[-20:]
print("異常データの判定結果:", y_pred_test.tolist())実行結果は次の通りです。
LOFの実行結果では、正常なデータは 1、異常なデータは -1 として判定されます。
学習データを投入した場合には、ほとんどの点が正常と判定されますが、クラスタの境界付近や局所的に密度が低い点については異常とみなされることがあります。これは、LOFが周囲の点との密度差を基準にしているため、完全に正常なデータであっても「周囲より浮いている」と判断されるケースがあるからです。
一方で、テストデータとして投入した異常値は、周囲の学習データ群と比べて明らかに孤立しているため、多くが -1 として異常判定されます。LOFは局所的な密度を比較するアルゴリズムであるため、クラスタが複数存在する場合でも、それぞれのクラスタ内で「浮いた点」を検出することが可能です。
このように、LOFの判定結果は「正常データの中にも一部異常判定される点がある」ことを示しており、これはアルゴリズムの特性上避けられない部分です。実務で利用する際には、n_neighbors や contamination といったハイパーパラメータを調整することで、異常検知の精度を改善することができます。
常データの判定結果: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, -1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, -1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, -1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
異常データの判定結果: [-1, 1, -1, 1, -1, 1, 1, 1, -1, -1, -1, 1, -1, -1, -1, -1, -1, -1, -1, -1]
可視化
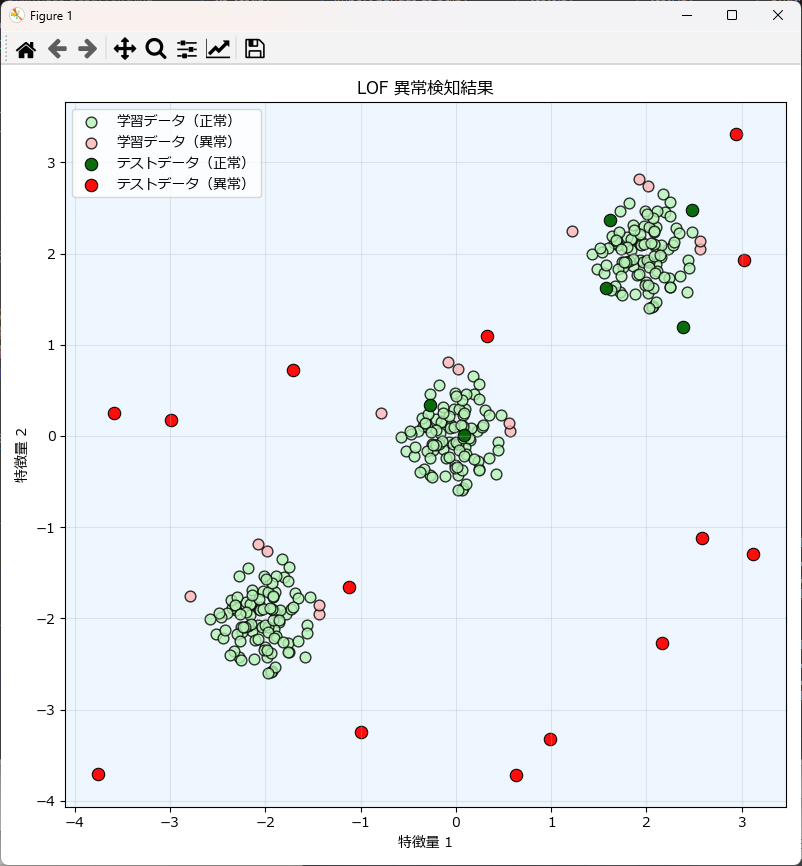
上記のグラフは、学習データ(正常)とテストデータ(異常)を散布図としてプロットしたものです。
先ほどのプログラムの末尾に下記のコードを丸ごと挿入してもらえればグラフが描画されます。関数化しているので、コピペしてお使いいただけます。
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
def plot_lof_results(X_train, y_train_pred, X_test, y_test_pred):
"""
LOF(Local Outlier Factor)の判定結果を2次元散布図で可視化する
"""
plt.figure(figsize=(8, 8))
# 背景色(薄いブルー)
ax = plt.gca()
ax.set_facecolor("#eef7ff")
# -------- 学習データ(薄い色・丸) --------
plt.scatter(
X_train[y_train_pred == 1, 0],
X_train[y_train_pred == 1, 1],
c="#b6f2b6", # 薄い緑
marker="o",
s=60,
alpha=0.8,
edgecolor="black",
label="学習データ(正常)"
)
plt.scatter(
X_train[y_train_pred == -1, 0],
X_train[y_train_pred == -1, 1],
c="#ffb6b6", # 薄い赤
marker="o",
s=60,
alpha=0.8,
edgecolor="black",
label="学習データ(異常)"
)
# -------- テストデータ(濃い色・★) --------
plt.scatter(
X_test[y_test_pred == 1, 0],
X_test[y_test_pred == 1, 1],
c="darkgreen",
marker="o",
s=80,
alpha=0.95,
edgecolor="black",
linewidth=0.8,
label="テストデータ(正常)"
)
plt.scatter(
X_test[y_test_pred == -1, 0],
X_test[y_test_pred == -1, 1],
c="red",
marker="o",
s=80,
alpha=0.95,
edgecolor="black",
linewidth=0.8,
label="テストデータ(異常)"
)
plt.title("LOF 異常検知結果")
plt.xlabel("特徴量 1")
plt.ylabel("特徴量 2")
plt.grid(True, alpha=0.3)
plt.legend()
plt.tight_layout()
plt.show()
# プロットを実行
plot_lof_results(
X_train=X_train,
y_train_pred=y_pred_train,
X_test=X_test,
y_test_pred=y_pred_test
)パラメータ調整とモデルの精度向上
LOF(Local Outlier Factor)の精度は、近傍点の選び方やスケーリング方法に大きく依存します。以下のパラメータを調整することで、異常検知性能を改善することが可能です。特に、データの分布やスケールに応じて適切な設定を行うことが重要です。
| パラメータ名 | 説明 | 調整のポイント |
|---|---|---|
| n_neighbors | 各サンプルの局所密度を計算する際に参照する近傍点の数 | 小さすぎるとノイズに敏感、大きすぎると異常が埋もれる。一般的に20前後がよく使われるが、データサイズや構造に応じて調整。 |
| contamination | データセットに含まれる異常データの割合を推定するパラメータ | 異常データの割合を事前にある程度把握している場合に有効。誤設定すると検出精度が低下するため注意。 |
| metric | 距離計算に用いる指標(例: 'euclidean', 'manhattan') | 数値データならユークリッド距離が一般的。特徴量のスケールが異なる場合は標準化が必須。 |
| p | Minkowski距離のパラメータ(metric='minkowski'の場合) | p=1でマンハッタン距離、p=2でユークリッド距離。データ特性に応じて選択。 |
| novelty | 新しいデータに対して異常判定を行うかどうか | Trueにすると学習後の新規データに対して予測可能。オンライン検知や運用環境で有効。 |
| n_jobs | 並列処理に使用するCPU数 | 大規模データでは計算効率を改善できる。 |
ハイパーパラメータの調整には、クロスバリデーションを活用するのが効果的です。例えば、GridSerchCV を用いて最適なパラメータを探索できます。
from sklearn.neighbors import LocalOutlierFactor
from sklearn.model_selection import GridSearchCV
import numpy as np
# LOFのハイパーパラメータの探索範囲を設定
param_lof_grid = {
# ★ 必須パラメータ 1: n_neighbors (近傍点の数)
# n_neighbors の値は、データセットのサイズや密度に応じて調整が必要です
'n_neighbors': [5, 10, 20, 30, 50],
# ★ 必須パラメータ 2: contamination (外れ値の割合)
# これはデータセット固有の値であり、モデル性能評価には直接関わりませんが、
# 決定境界を計算する際に閾値として使用されます。
'contamination': [0.01, 0.05, 0.1],
# metric: 距離計算に使用するメトリック
'metric': ['euclidean', 'manhattan'],
# p: Minkowski距離のパラメータ (metric='minkowski'の場合に有効)
# 例としてp=2 (Euclidean) と p=1 (Manhattan) を含めることもできます。
'p': [1, 2],
}
# LOFのGridSearchCVのインスタンスを作成
lof_grid_search = GridSearchCV(
LocalOutlierFactor(novelty=True),
param_lof_grid,
cv=5,
n_jobs=-1, # 並列処理で高速化
# 評価指標 (スコアリング): 異常検知では 'roc_auc' や 'neg_mean_squared_error' などを使用
# ただし、LOFは教師なしのため、ここでは単純なスコアリングを指定(実際の異常検知では工夫が必要)
scoring='neg_mean_squared_error'
)
# グリッドサーチを実行
# lof_grid_search.fit(X_train, y_train) # 評価指標を使う場合は y_train (異常/正常のラベル) が必要
# 最適なパラメータを表示
# print("Best parameters:", lof_grid_search.best_params_)ハイパーパラメータを調整しても異常検知の結果に満足できない場合は、特徴量エンジニアリングを行います。
例えば、正規化、標準化、分布の調整、標準偏差、分散、移動平均などの演算、他の特徴量との相関係数の利用などが考えられます。
また、OneClassSVM、AutoEncoderなど、別のアルゴリズムに切り替えることも検討すべきです。
LOFが簡単に使える自作クラス
LOFを簡単に使えるようにするために自作クラスとグラフ描画関数を作成しました。
このクラスのfit() メソッドは、1次元データが渡された場合、内部でreshape(-1, 1)で2次元に拡張しているため、問題なく処理できます。
異常検知を行うには
LOFは学習済みモデルを固定して使うのではなく、常に新しいデータを投入して異常検知を行う使い方が一般的です。学習データとありますが、これは異常検知対象のデータであると読み替えて下さい。
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# ここにLocalOutlierFactorUtilとグラフ描画関数のコードを張り付けるか、インポートしてください
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# 学習データの生成(3つのクラスターを生成)
np.random.seed(42)
X_train_data = 0.5 * np.random.randn(100, 2)
X_train_data = np.r_[X_train_data + 1, X_train_data - 1, X_train_data]
# 異常値(外れ値)をいくつか追加
outliers = 3 * np.random.randn(10, 2) + 10
X_train_data = np.r_[X_train_data, outliers]
df_train = pd.DataFrame(X_train_data, columns=['feature1', 'feature2'])
# インスタンスを生成
lof_util = LocalOutlierFactorUtil(df=df_train)
# モデルを学習し、学習データで異常検知を実施
# LOF (novelty=False) は fit_predict を実行し、結果を返します
model, y_pred_train = lof_util.fit(
column=['feature1', 'feature2'],
n_neighbors=20,
contamination=0.05,
novelty=False # ★ novelty=False: 学習データ内の異常検知
)
print("Train predictions (1:正常, -1:異常):", y_pred_train)
# --- グラフ描画 ---
plot_lof_results(
X_train=df_train[['feature1', 'feature2']].values,
y_train_pred=y_pred_train
)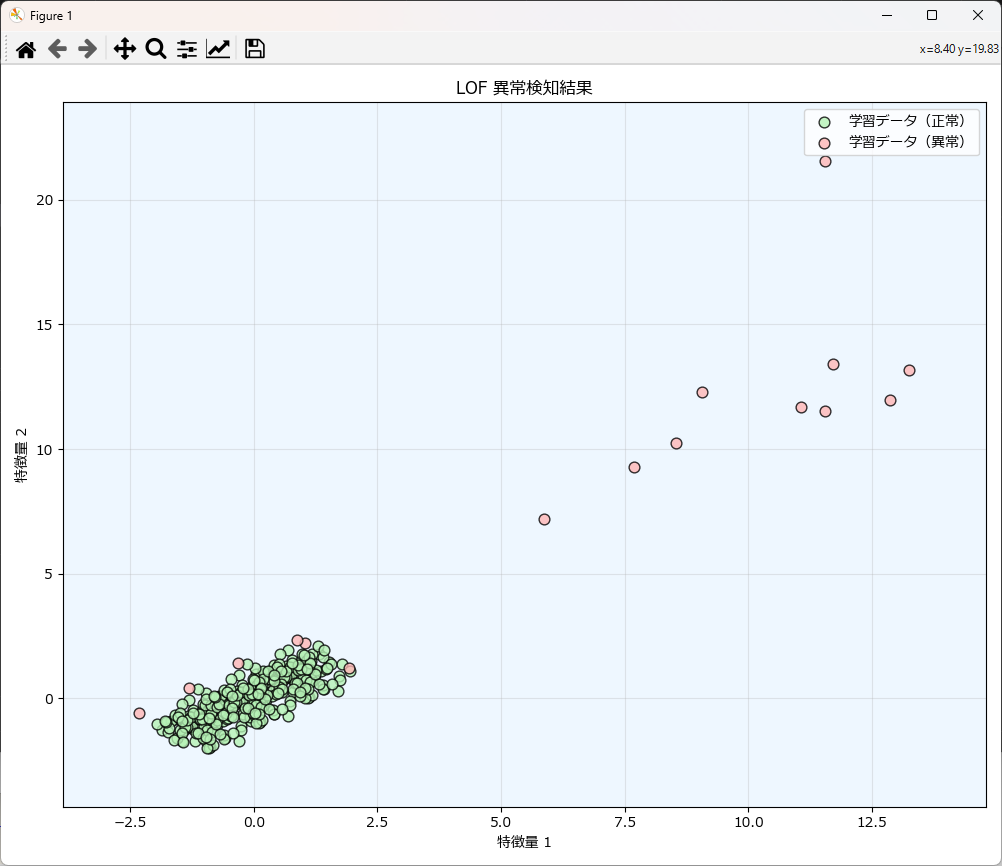
モデルを作成するには
LOFのデフォルトでは学習と予測が同時に行われる設計のため、モデルを保存することができません。モデルを保存するために、fitメソッドの novelty引数を True に設定する必要があります。
また、この場合はモデルを学習するだけで異常検知はしてくれませので、明示的に predictメソッドを呼び出して異常検知を行います。
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# ここにLocalOutlierFactorUtilとグラフ描画関数のコードを張り付けるか、インポートしてください
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# --- データの生成 ---
np.random.seed(42)
# 正常データ群 (3つのクラスター)
X_train_data = 0.5 * np.random.randn(100, 2)
X_train_data = np.r_[X_train_data + 1, X_train_data - 1, X_train_data]
df_train = pd.DataFrame(X_train_data, columns=['feature1', 'feature2'])
# テストデータ生成(一部を異常値とする)
np.random.seed(20)
X_test_normal = 0.5 * np.random.randn(50, 2) + 0.5
X_test_outliers = 3 * np.random.randn(5, 2) + 10 # 異常値
X_test_data = np.r_[X_test_normal, X_test_outliers]
df_test = pd.DataFrame(X_test_data, columns=['feature1', 'feature2'])
# インスタンスを生成
lof_util = LocalOutlierFactorUtil(df=df_train)
# novelty=True で学習(fit のみ実行)
model_trained, _ = lof_util.fit(column=['feature1', 'feature2'], n_neighbors=20, contamination=0.05, novelty=True)
# モデルを保存
MODEL_PATH = 'lof_novelty_model.pkl'
lof_util.save_model(MODEL_PATH)
# 異常検知の実行
y_pred_test = lof_util.predict(column=['feature1', 'feature2'])
print(f"テストデータ中の異常値 (-1) の数: {np.sum(y_pred_test == -1)}")
print(f"テストデータ中の正常値 (1) の数: {np.sum(y_pred_test == 1)}")
# 学習データに対する予測を実行
y_pred_train_for_plot = lof_util.predict(column=['feature1', 'feature2'])
plot_lof_results(
X_train=df_train[['feature1', 'feature2']].values,
y_train_pred=y_pred_train_for_plot,
model=lof_util.model
)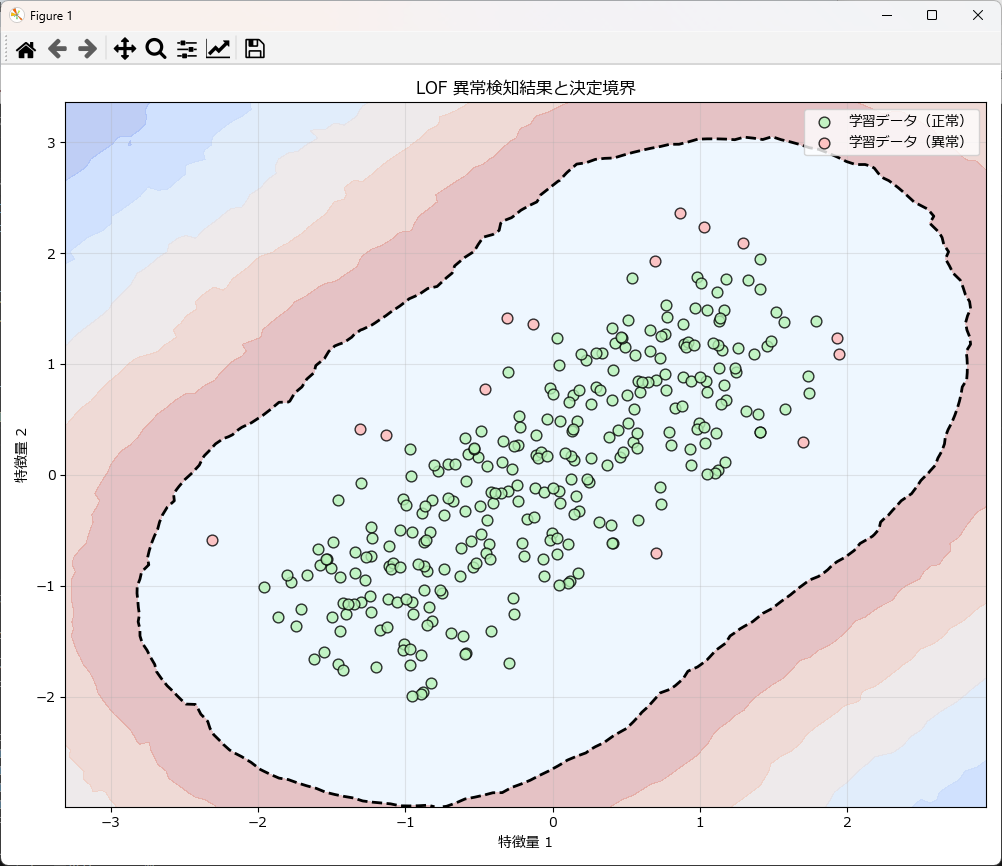
新しいデータで異常検知するには
学習済みモデルをファイルに保存し、それを読み込んで利用することで新しいデータの異常検知が行えます。
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# ここにLocalOutlierFactorUtilとグラフ描画関数のコードを張り付けるか、インポートしてください
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# 学習データの生成
np.random.seed(42)
X_train_data = 0.5 * np.random.randn(100, 2)
X_train_data = np.r_[X_train_data + 1, X_train_data - 1, X_train_data]
df_train = pd.DataFrame(X_train_data, columns=['feature1', 'feature2'])
# インスタンスを生成
lof_util = LocalOutlierFactorUtil(df_train)
# novelty=True で学習(fit のみ実行)
model_trained, _ = lof_util.fit(column=['feature1', 'feature2'], n_neighbors=20, contamination=0.05, novelty=True)
# 異常検知の実行
y_pred_test = lof_util.predict(column=['feature1', 'feature2'])
# 学習データの結果
plot_lof_results(X_train=X_train_data, y_train_pred=y_pred_test,model=lof_util.model)
# モデルを保存
MODEL_PATH = 'lof_novelty_model.pkl'
lof_util.save_model(MODEL_PATH)
# LOF モデルのロード
lof_util = LocalOutlierFactorUtil(model_path=MODEL_PATH)
# テストデータの生成
np.random.seed(20)
X_test_data = np.random.uniform(low=-4, high=4, size=(100, 2))
df_test = pd.DataFrame(X_test_data, columns=['feature1', 'feature2'])
# 新しいデータで異常検知
y_pred_test = lof_util.predict(['feature1', 'feature2'], df=df_test)
print("Test predictions:", y_pred_test)
## テストデータの結果
plot_lof_results(X_train=X_test_data, y_train_pred=y_pred_test,model=lof_util.model)学習時の異常検知結果
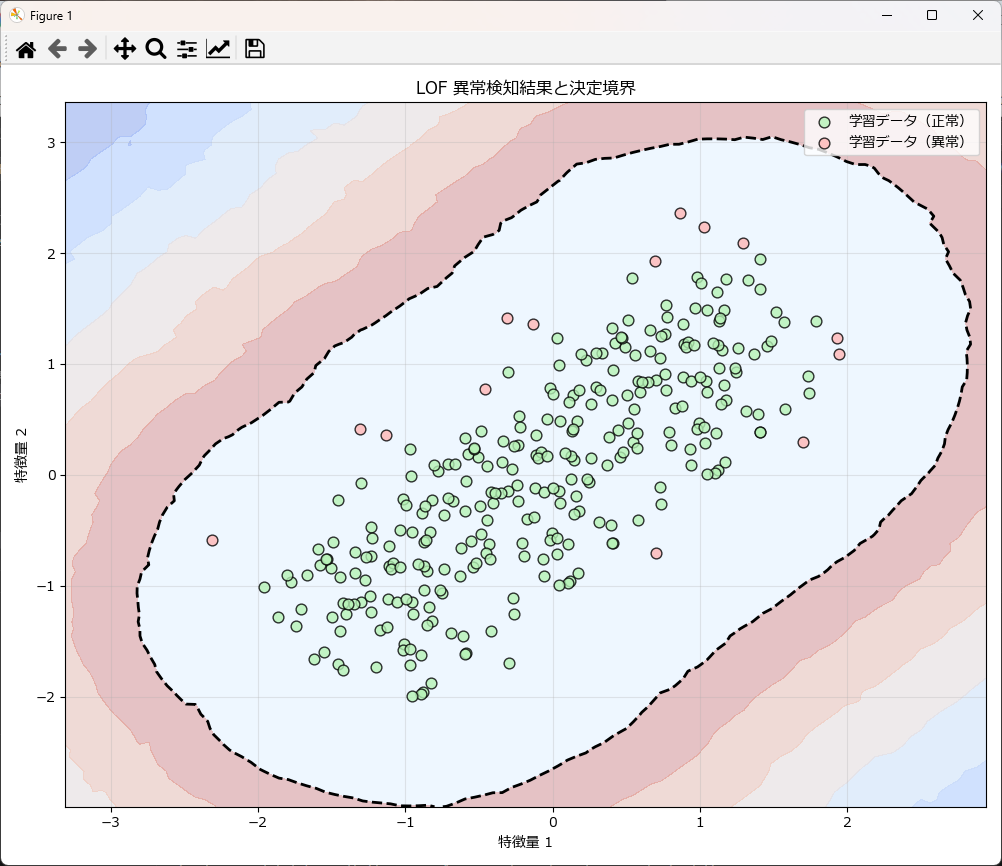
学習済みモデルに新しいデータで異常検知した結果
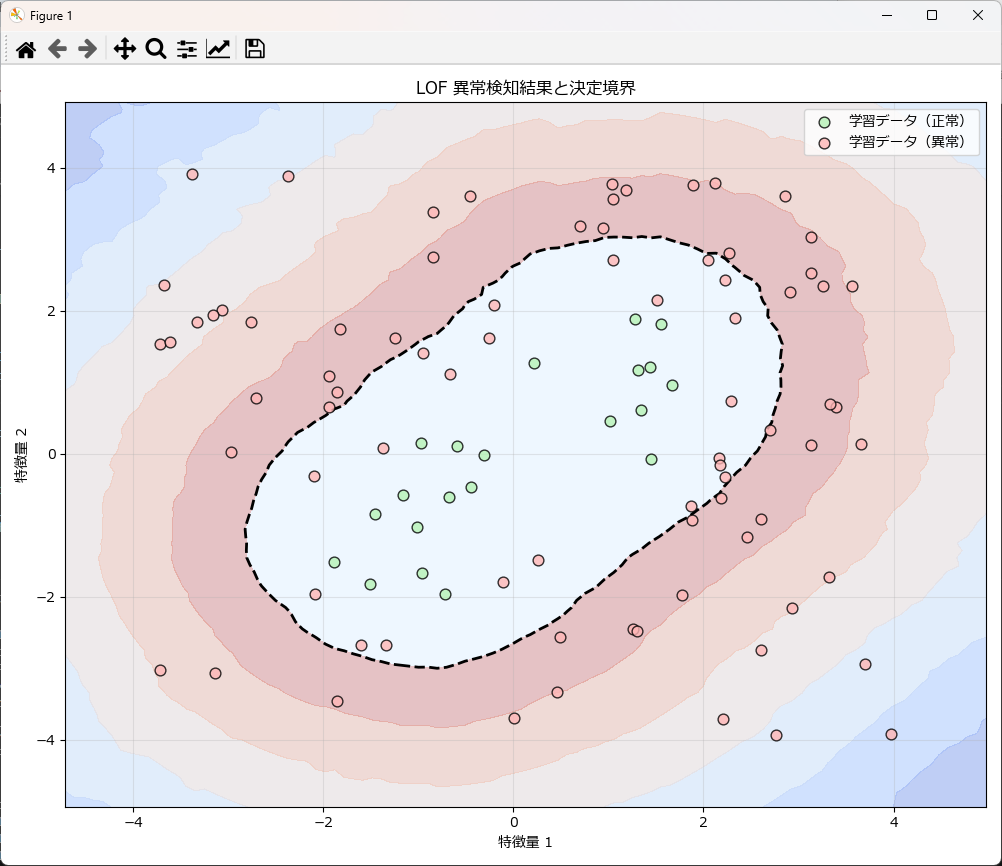
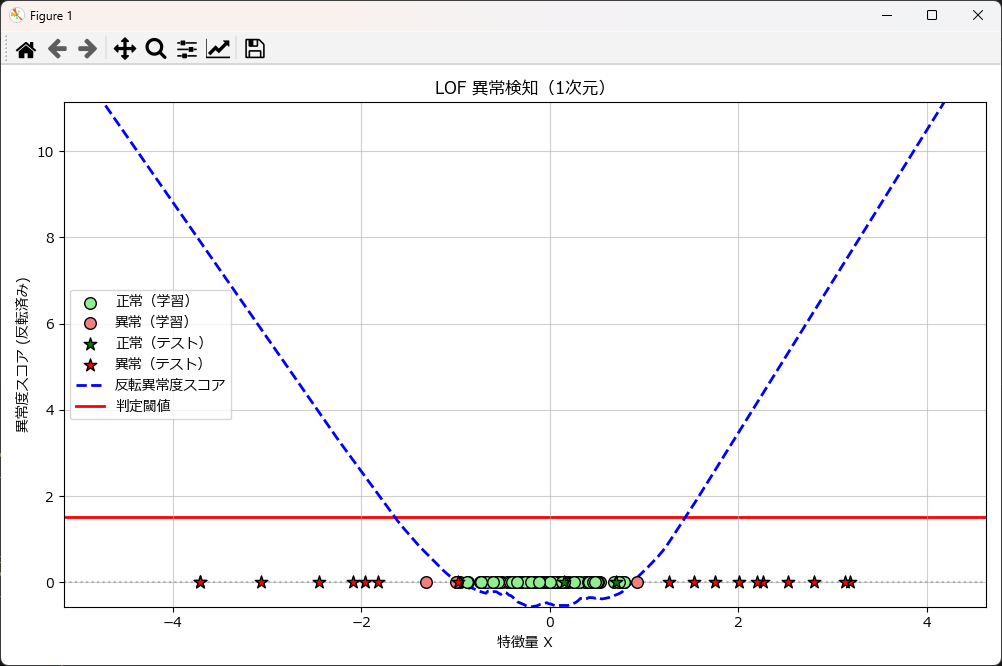
1次元の異常検知をするには
LocalOutlierFactorUtilクラスの使い方は前述と全く同じですが、グラフ描画は plot_lof_results_1dを使用します。
# 学習データの生成
np.random.seed(42)
X_train_data = 0.5 * np.random.randn(100).reshape(-1, 1)
df_train = pd.DataFrame(X_train_data, columns=['feature1'])
# インスタンスを生成
lof_util = LocalOutlierFactorUtil(df_train)
# モデルを学習 (fit を使用し、novelty=True に設定)
model_trained, _ = lof_util.fit(column=['feature1'], n_neighbors=20, contamination=0.05, novelty=True)
# 学習データでの異常検知を実施 (可視化のために明示的に predict を実行)
y_pred_train = lof_util.predict(['feature1'])
print("Train predictions:", y_pred_train)
# テストデータを生成
np.random.seed(20)
# 異常値を含む広範囲のデータを作成
X_test_data = np.random.uniform(low=-4, high=4, size=(20,)).reshape(-1, 1)
df_test = pd.DataFrame(X_test_data, columns=['feature1'])
# テストデータで異常検知を実施
y_pred_test = lof_util.predict(['feature1'], df=df_test)
print("Test predictions:", y_pred_test)
# 1次元用の関数を使ってグラフ描画 ---
plot_lof_results_1d(X_train=df_train[['feature1']].values,
y_train_pred=y_pred_train,
X_test=df_test[['feature1']].values,
y_test_pred=y_pred_test,
model=lof_util.model
)
LocalOutlierFactorUtilクラスとグラフ描画関数リファレンス
| LocalOutlierFactorUtilのグラフ描画関数 | 説明 |
|---|---|
| plot_lof_results_1d( X_train=None, y_pred_train=None, X_test=None, y_pred_test=None, model ) | 1次元データのLOFの結果をプロットする。学習データとテストデータを表示し、決定境界を描画する。 |
| plot_lof_results( X_train=None, y_pred_train=None, X_test=None, y_pred_test=None, model ) | 2次元データのLOFの結果をプロットする。学習データとテストデータを表示し、決定境界を描画する。 |
| LocalOutlierFactorUtilのメソッド | 説明 |
|---|---|
| __init__(df=None, model_path=None) | クラスの初期化メソッド。データフレームとモデルパスを受け取る。 |
| fit(column, nu=0.1, gamma="auto", kernel="rbf") | LOFモデルを作成・学習するメソッド。指定したカラムを使用。 |
| predict(column, df=None) | 学習したモデルを使用して予測を行うメソッド。指定したカラムを使用。 |
| read_csv(file_name, encoding="shift-jis") | CSVファイルからデータを読み込むメソッド。 |
| save_model(model_path) | 学習したモデルをファイルに保存するメソッド。 |
| load_model(model_path=None) | モデルをファイルから読み込むメソッド。 |
LocalOutlierFactorUtilクラスとグラフ描画関数のソースコード
from sklearn.neighbors import LocalOutlierFactor
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import rcParams
import joblib # ★ joblib をインポート
import os
rcParams['font.family'] = 'Meiryo'
class LocalOutlierFactorUtil:
def __init__(self, df=None, model_path=None):
self.df = None if df is None else df.copy()
self.model = None
self.y_train_pred = None
# model_path が指定されていればロードを試みる
if model_path:
self.load_model(model_path)
def fit(self, column, n_neighbors=20, contamination=0.05, novelty=False):
"""
LOFモデルの作成と学習。novelty=False で学習データの fit_predict を行う。
"""
if self.df is None:
raise ValueError("DataFrameがセットされていません。")
if isinstance(column, list) and len(column) > 1:
X = self.df[column].values
else:
X = self.df[column].values.reshape(-1, 1)
# LOF は novelty=True なら predict が可能になる(sklearn 0.22+)
self.model = LocalOutlierFactor(
n_neighbors=n_neighbors,
contamination=contamination,
novelty=novelty
)
# novelty=True の場合、学習データは fit のみ
if novelty:
self.model.fit(X)
self.y_train_pred = None
# novelty=False の場合 fit_predict が必要
else:
self.y_train_pred = self.model.fit_predict(X)
return self.model, self.y_train_pred
def predict(self, column, df = None):
"""
LOF で新しいデータを判定する。novelty=True の場合のみ使用可能。
"""
if self.model is None:
raise RuntimeError("モデルが学習またはロードされていません。")
if not hasattr(self.model, "predict"):
raise RuntimeError("この LOF モデルは novelty=False のため predict できません。novelty=True で学習してください。")
# df がNoneでなければ、インスタンス変数に代入
if df is not None:
self.df = df
if isinstance(column, list) and len(column) > 1:
X = self.df[column].values
else:
X = self.df[column].values.reshape(-1, 1)
return self.model.predict(X)
def save_model(self, path):
"""
学習済みモデルを joblib でファイルに保存する。
"""
if self.model is None:
raise RuntimeError("モデルが学習されていません。")
if not self.model.novelty:
print("警告: novelty=False のモデルは、学習データを保持するため、通常は保存・再利用に適しません。")
joblib.dump(self.model, path)
print(f"モデルを {path} に保存しました。")
def load_model(self, path):
"""
joblib で保存されたモデルをロードする。
"""
if not os.path.exists(path):
raise FileNotFoundError(f"ファイルが見つかりません: {path}")
self.model = joblib.load(path)
print(f"モデルを {path} からロードしました。")
# novelty=True のモデルがロードされたか確認
if not hasattr(self.model, "predict"):
print("警告: ロードされたモデルは novelty=False のため、predict メソッドが使えません。")
return self.model
import numpy as np
import matplotlib.pyplot as plt
def plot_lof_results_1d(X_train=None, y_train_pred=None,
X_test=None, y_test_pred=None, model=None): # modelを最後に移動し、デフォルト値をNoneに
"""
LOF の 1次元結果をプロット。
モデルが渡された場合、異常度スコア(decision_function)を反転させて可視化します。
"""
plt.figure(figsize=(10, 6))
ax = plt.gca()
# --- データのプロット (X軸: 特徴量, Y軸: 0) ---
# 学習データ
if X_train is not None and y_train_pred is not None:
# X_train は (N, 1) の形状を想定
X_train_flat = X_train.flatten()
plt.scatter(X_train_flat[y_train_pred == 1],
np.zeros_like(X_train_flat[y_train_pred == 1]),
c='lightgreen', edgecolors='k', s=70, label="正常(学習)", zorder=3)
plt.scatter(X_train_flat[y_train_pred == -1],
np.zeros_like(X_train_flat[y_train_pred == -1]),
c='lightcoral', edgecolors='k', s=70, label="異常(学習)", zorder=3)
# テストデータ
if X_test is not None and y_test_pred is not None:
X_test_flat = X_test.flatten()
plt.scatter(X_test_flat[y_test_pred == 1],
np.zeros_like(X_test_flat[y_test_pred == 1]),
c='green', edgecolors='k', s=90, marker='*',
label="正常(テスト)", zorder=4)
plt.scatter(X_test_flat[y_test_pred == -1],
np.zeros_like(X_test_flat[y_test_pred == -1]),
c='red', edgecolors='k', s=90, marker='*',
label="異常(テスト)", zorder=4)
# --- 決定関数プロット (モデルが存在する場合のみ実行) ---
# プロット対象のデータ(X)が存在し、かつモデルが渡された場合
if (X_train is not None or X_test is not None) and model is not None:
# 描画範囲を決定するために全てのデータを結合
xx = np.concatenate([arr.flatten() for arr in [X_train, X_test] if arr is not None])
x_range = np.linspace(xx.min() - 1, xx.max() + 1, 400).reshape(-1, 1)
try:
# LOFの決定関数 Z を計算し、反転させる (反転後: 値が大きいほど異常度が高い)
Z = -model.decision_function(x_range)
# 決定関数をプロット
plt.plot(x_range, Z, color='blue', linestyle='--', linewidth=2, label="反転異常度スコア", zorder=2)
# 異常の閾値(境界)を示す線
if hasattr(model, 'offset_'):
# Sklearn 0.22+の novelty=True で学習した場合に利用可能
threshold = -model.offset_
else:
# 訓練データから閾値を計算(novelty=False の場合)
if X_train is not None:
raw_scores = model.decision_function(X_train.reshape(-1, 1))
threshold = -np.percentile(raw_scores, 100. * (1. - model.contamination))
else:
# 簡易的な可視化のため、Zの範囲とcontaminationから暫定閾値を計算
threshold = Z.min() + (Z.max() - Z.min()) * model.contamination
plt.axhline(threshold, color='red', linestyle='-', linewidth=2, label="判定閾値", zorder=1)
# Y軸の範囲をスコアに合わせて調整し、データ点のY軸 (0) も含むようにする
min_z, max_z = Z.min(), Z.max()
y_lim_min = min(min_z, -0.5)
y_lim_max = max(max_z, 0.5)
plt.ylim(y_lim_min, y_lim_max)
except AttributeError:
print("警告: モデルに decision_function がないため、スコアカーブはスキップされます。")
# データ点のY軸位置
plt.axhline(0, color='gray', linestyle=':', alpha=0.5)
# --- グラフの体裁 ---
title_suffix = "とスコアカーブ" if model is not None else ""
plt.title(f"LOF 異常検知(1次元){title_suffix}")
plt.xlabel("特徴量 X")
plt.ylabel("異常度スコア (反転済み)")
plt.grid(True, alpha=0.6)
plt.legend()
plt.tight_layout()
plt.show()
def plot_lof_results(X_train=None, y_train_pred=None, X_test=None, y_test_pred=None, model=None):
"""
LOF の 2次元結果をプロットします。
モデルが渡された場合、決定境界を背景に描画します。
Parameters
----------
X_train : np.ndarray, optional
学習データの特徴量 (N, 2)。
y_train_pred : np.ndarray, optional
学習データの LOF 判定結果 (1:正常, -1:異常)。
X_test : np.ndarray, optional
テストデータの特徴量 (N, 2)。
y_test_pred : np.ndarray, optional
テストデータの LOF 判定結果 (1:正常, -1:異常)。
model : object, optional
学習済みの LOF モデルオブジェクト。Noneの場合、決定境界は描画しません。
"""
plt.figure(figsize=(10, 8))
ax = plt.gca()
# ★ 1. データを結合し、プロット範囲を決定(常に実行)
all_data_arrays = [arr for arr in [X_train, X_test] if arr is not None]
if all_data_arrays:
X = np.concatenate(all_data_arrays)
# --- 2. 決定境界の計算と描画 (モデルとデータが提供された場合のみ実行) ---
if model is not None and all_data_arrays:
# 描画範囲を決定
x_min_plot, x_max_plot = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min_plot, y_max_plot = X[:, 1].min() - 1, X[:, 1].max() + 1
# グリッドを作成
xx, yy = np.meshgrid(np.linspace(x_min_plot, x_max_plot, 100),
np.linspace(y_min_plot, y_max_plot, 100))
# モデルの決定関数を使って異常度スコアを計算 (Z)
try:
Z = model.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
except AttributeError as e:
print(f"警告: モデルに decision_function がありません。決定境界はスキップされます。エラー: {e}")
Z = None # スコア計算に失敗した場合、決定境界の描画をスキップ
if Z is not None:
# 閾値(決定境界)を計算
if hasattr(model, 'offset_'):
threshold = model.offset_
elif X_train is not None and hasattr(model, 'contamination'):
# 訓練データから生の閾値を計算
raw_scores = model.decision_function(X_train)
threshold = np.percentile(raw_scores, 100. * (1. - model.contamination))
else:
threshold = 0.0 # 代替値
# 背景色(異常度スコアの等高線塗りつぶし)
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), threshold, 7),
cmap=plt.cm.coolwarm, alpha=0.3)
# 決定境界線
plt.contour(xx, yy, Z, levels=[threshold], linewidths=2, colors='black', linestyles='--')
# 決定境界を描画する場合、軸の範囲も設定
plt.xlim(x_min_plot, x_max_plot)
plt.ylim(y_min_plot, y_max_plot)
# --- 3. データ点の描画 (ロジック) ---
# データが存在する場合のみ背景色を設定
if all_data_arrays:
ax.set_facecolor("#eef7ff")
# 学習データが存在する場合
if X_train is not None and y_train_pred is not None:
plt.scatter(X_train[y_train_pred == 1, 0], X_train[y_train_pred == 1, 1],
c="#b6f2b6", marker="o", s=60, alpha=0.8, edgecolor="black", label="学習データ(正常)", zorder=3)
plt.scatter(X_train[y_train_pred == -1, 0], X_train[y_train_pred == -1, 1],
c="#ffb6b6", marker="o", s=60, alpha=0.8, edgecolor="black", label="学習データ(異常)", zorder=3)
# テストデータが存在する場合
if X_test is not None and y_test_pred is not None:
plt.scatter(X_test[y_test_pred == 1, 0], X_test[y_test_pred == 1, 1],
c="green", marker="o", s=80, alpha=0.95, edgecolor="black", linewidth=0.8, label="テストデータ(正常)", zorder=4)
plt.scatter(X_test[y_test_pred == -1, 0], X_test[y_test_pred == -1, 1],
c="red", marker="o", s=80, alpha=0.95, edgecolor="black", linewidth=0.8, label="テストデータ(異常)", zorder=4)
# --- 4. グラフの体裁 ---
# ★ モデルが None の場合、データに基づいて軸の範囲を自動調整
if model is None and all_data_arrays:
# データの外側に少し余白を持たせる (描画がscatterに任せきりになるのを防ぐ)
x_min, x_max = X[:, 0].min(), X[:, 0].max()
y_min, y_max = X[:, 1].min(), X[:, 1].max()
x_padding = (x_max - x_min) * 0.1 if (x_max - x_min) > 0 else 1
y_padding = (y_max - y_min) * 0.1 if (y_max - y_min) > 0 else 1
plt.xlim(x_min - x_padding, x_max + x_padding)
plt.ylim(y_min - y_padding, y_max + y_padding)
title_suffix = "と決定境界" if model is not None else ""
plt.title(f"LOF 異常検知結果{title_suffix}")
plt.xlabel("特徴量 1")
plt.ylabel("特徴量 2")
plt.grid(True, alpha=0.3)
plt.legend()
plt.tight_layout()
plt.show()まとめ
本記事では、 近年注目を集める異常検知技術のなかでも、特にLocal Outlier Factor (LOF) アルゴリズムの詳細と、その強力な応用範囲について解説しました。
LOF は、異常検知に非常に効果的なアルゴリズムであり、特に製造業における設備保全(予知保全/PdM)や品質管理の自動化で幅広く活用されています。
LOF の最大の強みは、その名が示す通り、「局所的な」密度の差に着目する点にあります。データ全体から離れているかどうかではなく、周囲のデータ点と比較してどのくらい異質な密度を持つかを評価するため、複雑なデータ構造や多クラスのデータ、あるいは異常な状態が局所的に発生する状況(例:機械の特定部品の摩耗)において、高い精度を発揮します。
この記事が、皆さんの異常検知に役立てていただければ幸いです。








コメント