アンサンブル回帰モデル(LightGBMやXGBoostなど)を使って高精度な予測を目指すとき、最大のカギとなるのが「どの特徴量を使うか?」という選定プロセスです。
本記事では、“効く特徴量”を自動で見つけるための手法として、Forward SelectionとBackward Eliminationを解説します。
実務でそのまま使えるコピペOKのPythonコード付きで、特徴量選定の流れをステップバイステップで紹介します。 「精度を上げたい」「変数が多すぎて困っている」「解釈性も大事にしたい」これらの内容に興味のある方は、ぜひご一読ください。
Forward Selection / Backward Eliminationとは
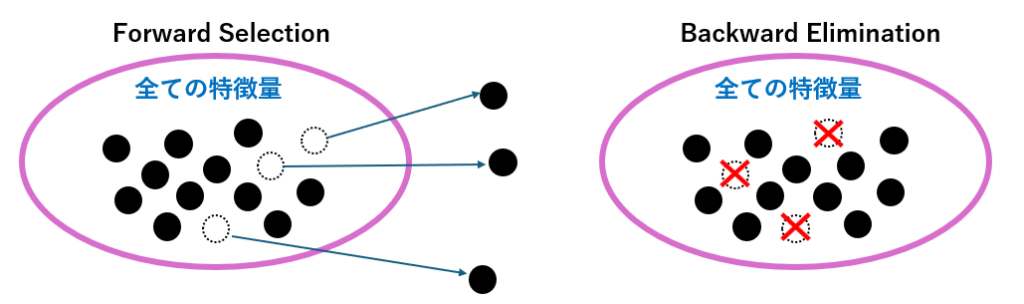
機械学習モデルの性能を最大限に引き出すには、「どの特徴量を使うか?」の選定がとても重要です。 特に、特徴量が多い場合や、意味のない変数が混ざっている場合、不要な特徴量を取り除くことで精度の向上・過学習の抑制・解釈性の向上が期待できます。
このような特徴量選定の代表的な手法が、Forward Selection(前進選択)とBackward Elimination(後退除去)です。
Forward Selection(前進選択)
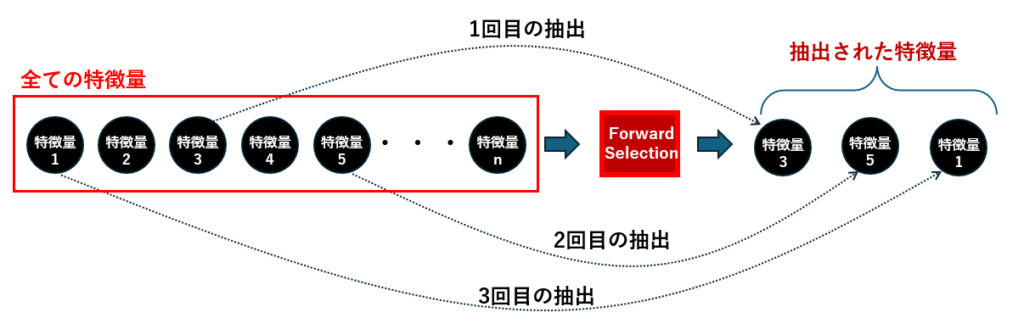
各ステップで最も効果的な特徴量が選ばれ、最終的に
特徴量3、特徴量5、特徴量1 の3つが抽出された。Forward Selectionは、空の特徴量セットからスタートし、モデルの性能が最も改善される特徴量を1つずつ追加していく手法です。
- すべての特徴量の中から、最もスコアが良くなる1つを選ぶ
- すでに選ばれた特徴量に加えて、次に良くなる特徴量を追加
- 指定した条件(スコアの改善が止まる、上限数に達するなど)で終了
Backward Elimination(後退除去)

最終的に
特徴量2、特徴量4、特徴量10 が残り、モデルにとって重要と判断された。Backward Eliminationは、すべての特徴量を使った状態からスタートし、影響の小さい特徴量を1つずつ削除していく手法です。
- 全特徴量でモデルを学習
- 最も影響の小さい特徴量を1つ除外
- スコアが悪化しない限り、除外を繰り返す
ForwardとBackwardの比較と使い分けのポイント
Forwardは「初期探索やベースライン構築」、Backwardは「本番運用前のモデル圧縮や説明性の強化」でよく使われます。
以下は両者の比較結果です。
| 比較項目 | Forward Selection | Backward Elimination |
|---|---|---|
| 開始点 | 空の特徴量セット | 全特徴量を使用 |
| 操作 | 特徴量を追加 | 特徴量を削除 |
| 処理コスト | 低め(特徴量が多いと有利) | 高め(全特徴量で学習) |
| 特徴量の見落とし | 可能性あり | 少ない |
| 解釈性 | 構築過程が明確 | 残った特徴量が明確 |
| 向いている状況 | ・特徴量の数が多く過学習の可能性大 ・計算コストを抑えたい ・効く変数だけで素早くモデルを作りたい | ・モデルの解釈性を高めたい ・不要な変数を削りモデルをシンプルにしたい ・変数が少なく全探索でもコストが許容範囲 |
| 主な活用シーン | 初期探索やベースライン構築 | 本番運用前のモデル圧縮や説明性の強化 |
主なシナリオごとに、どちらが適切かをまとめてみました。
| シナリオ | おすすめ手法 | 理由 |
|---|---|---|
| 特徴量が多く、過学習が心配 | Forward Selection | 少数の強い特徴量だけで高精度モデルが作れる |
| モデルの解釈性を高めたい | Backward Elimination | 不要な特徴量を削ってスリム化できる |
| モデルの軽量化が必要 | どちらも可(Forward推奨) | 少数特徴量で十分な精度が出るならForwardが効率的 |
| 特徴量の相互作用が重要 | Forward(慎重に) | アンサンブルは相互作用を捉えるので、削除は慎重に |
回帰モデルで使うときの注意点
アンサンブル回帰において、Forward Selection は相性が抜群です。
アンサンブル回帰(特にLightGBMやXGBoost)は、非線形な関係や特徴量間の相互作用を自動で捉えるのが得意です。そのため、少数の“効く特徴量”だけでも高精度なモデルを構築しやすいという特徴があります。
Forward Selectionは、効く特徴量を順に追加していくので、アンサンブルの“少数精鋭で戦える”特性と相性がいい!
その一方、Backward Elimination の場合は注意が必要です。
アンサンブル回帰は、特徴量の重要度を自動で調整する能力が高いため、無理に特徴量を削らなくても、ある程度のノイズ耐性があります。
解釈性を高めたいときや、モデルを圧縮したいときには有効ですが、特徴量間の相互作用を考慮せずに1変数ずつ削除すると、重要な組み合わせを壊すリスクもあります。
変数が少ない場合や、モデルの簡素化が目的のときに慎重に使うのがお勧めです。
Forward Selectionによる特徴量選定
下記は、Forward Selectionを使った特徴量選定のサンプルプログラムです。関数化していますので、このままコピペしてお使いいただけます。
動作確認のため、sklearnが用意しているmake_regression 関数を使ってダミーデータを生成し、それを使うようになっています。
make_regression は、線形回帰のテスト用に使える合成データを生成する関数です。 特徴量と目的変数の間に、線形関係とノイズを含んだデータを作成できます。 今回はこの関数を使って、1000サンプル・10特徴量の回帰用ダミーデータを作成しました。 各特徴量(feature_0〜feature_9)は平均0・分散1の標準正規分布から生成され、 目的変数は の形で計算されています。
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import cross_val_score
import numpy as np
def forward_selection(X, y, model, scoring='neg_root_mean_squared_error', max_features=None, cv=5, verbose=True):
"""
Forward Selection による特徴量選定
Parameters:
----------
X : pd.DataFrame
特徴量データ
y : pd.Series or np.array
目的変数
model : sklearn互換の回帰モデル
例:LGBMRegressor(), XGBRegressor(), etc.
scoring : str
スコアリング指標(sklearnのcross_val_scoreと同じ形式)
max_features : int or None
選定する最大特徴量数(Noneなら全特徴量が対象)
cv : int
クロスバリデーションの分割数
verbose : bool
Trueなら進捗を表示
Returns:
-------
selected_features : list
選ばれた特徴量のリスト
scores : list
各ステップでのスコア
"""
remaining = list(X.columns)
selected = []
best_score = -np.inf
scores = []
while remaining:
scores_candidates = []
for feature in remaining:
trial_features = selected + [feature]
score = cross_val_score(model, X[trial_features], y, scoring=scoring, cv=cv).mean()
scores_candidates.append((score, feature))
scores_candidates.sort(reverse=True)
best_candidate_score, best_candidate = scores_candidates[0]
if verbose:
print(f"Trying: {best_candidate}, Score: {best_candidate_score:.5f}")
if best_candidate_score > best_score:
selected.append(best_candidate)
remaining.remove(best_candidate)
best_score = best_candidate_score
scores.append(best_candidate_score)
else:
break
if max_features and len(selected) >= max_features:
break
return selected, scores
if __name__ == "__main__":
# =======================================================
# ダミーデータの作成
# =======================================================
import pandas as pd
from sklearn.datasets import make_regression
# 1000サンプル、10特徴量のダミーデータを作成
X_array, y = make_regression(n_samples=1000, n_features=10, noise=0.1, random_state=42)
X = pd.DataFrame(X_array, columns=[f"feature_{i}" for i in range(X_array.shape[1])])
# =======================================================
# Forward Selectionの実行
# =======================================================
from lightgbm import LGBMRegressor
# 例:モデルとデータを用意(X, y は事前に定義されている前提)
model = LGBMRegressor()
selected_features, scores = forward_selection(X, y, model)
print("選ばれた特徴量:", selected_features)
print("各ステップのスコア:", scores)
実行結果は以下の通りです。
Trying: feature_8, Score: -34.03136
選ばれた特徴量: ['feature_3', 'feature_6', 'feature_9', 'feature_0', 'feature_1', 'feature_2', 'feature_5', 'feature_7']
各ステップのスコア: [np.float64(-112.7918066375006), np.float64(-93.26256456679629), np.float64(-67.08958605715839), np.float64(-56.13388070558975), np.float64(-46.63592807259725), np.float64(-36.03528039817384), np.float64(-34.91637709985585), np.float64(-33.75101498811903)]
選ばれた特徴量は、モデルの性能を最も改善した順に並んでいます。 今回の例では、feature_3 を最初に追加することで最もスコアが改善され、 次いで feature_6、feature_9…と、追加するごとにモデルの精度が向上していった順番になっています。
この順序は、あくまで「このモデル・このデータ・このスコア指標において、どの特徴量が最も効果的だったか」を示すものです。 今回は scoring='neg_root_mean_squared_error'、つまり RMSE(二乗平均平方根誤差) を評価指標として使用しています。 そのため、他のモデルやスコア指標(例:R²やMAEなど)を使うと、選ばれる特徴量や順番が変わる可能性があります。
Backward Eliminationよる特徴量選定
下記は、Backward Eliminationを使った特徴量選定のサンプルプログラムです。関数化していますので、このままコピペしてお使いいただけます。
ダミーデータは前述と同様にmake_regression を使っています。
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import cross_val_score
import numpy as np
def backward_elimination(X, y, model, scoring='neg_root_mean_squared_error', min_features=1, cv=5, verbose=True):
"""
Backward Elimination による特徴量選定
Parameters:
----------
X : pd.DataFrame
特徴量データ
y : pd.Series or np.array
目的変数
model : sklearn互換の回帰モデル
scoring : str
スコアリング指標(sklearn形式)
min_features : int
最低限残す特徴量数
cv : int
クロスバリデーションの分割数
verbose : bool
Trueなら進捗を表示
Returns:
-------
selected_features : list
最終的に残った特徴量
scores : list
各ステップでのスコア
"""
selected = list(X.columns)
scores = []
best_score = cross_val_score(model, X[selected], y, scoring=scoring, cv=cv).mean()
scores.append(best_score)
while len(selected) > min_features:
scores_candidates = []
for feature in selected:
trial_features = [f for f in selected if f != feature]
score = cross_val_score(model, X[trial_features], y, scoring=scoring, cv=cv).mean()
scores_candidates.append((score, feature))
scores_candidates.sort(reverse=True)
best_candidate_score, worst_feature = scores_candidates[0]
if verbose:
print(f"Removing: {worst_feature}, Score: {best_candidate_score:.5f}")
if best_candidate_score >= best_score:
selected.remove(worst_feature)
best_score = best_candidate_score
scores.append(best_candidate_score)
else:
break
return selected, scores
if __name__ == "__main__":
# =======================================================
# ダミーデータの作成
# =======================================================
import pandas as pd
from sklearn.datasets import make_regression
# 1000サンプル、10特徴量のダミーデータを作成
X_array, y = make_regression(n_samples=1000, n_features=10, noise=0.1, random_state=42)
X = pd.DataFrame(X_array, columns=[f"feature_{i}" for i in range(X_array.shape[1])])
# =======================================================
# Backward Eliminationの実行
# =======================================================
from lightgbm import LGBMRegressor
import pandas as pd
# モデル定義
model = LGBMRegressor()
# 特徴量選定
selected_features, scores = backward_elimination(X, y, model)
print("残った特徴量:", selected_features)
print("各ステップのスコア:", scores)
結果は次の通りです。
Removing: feature_7, Score: -34.91638
残った特徴量: ['feature_0', 'feature_1', 'feature_2', 'feature_3', 'feature_5', 'feature_6', 'feature_7', 'feature_9']
各ステップのスコア: [np.float64(-34.560877694950555), np.float64(-34.03136155807114), np.float64(-33.75101498811903)]
残った特徴量は、削除するとスコアが悪化するため、モデルにとって重要と判断された順番になっています。 今回の例では、feature_7 を削除した時点でスコアが悪化し始めたため、 feature_0、feature_1、feature_2、feature_3、feature_5、feature_6、feature_7、feature_9 の8つが最終的に残りました。
まとめ
本記事では、特徴量選定の代表的な手法である Forward Selection と Backward Elimination を使って、 回帰モデルにおける重要な特徴量の見つけ方を実践的に紹介しました。
- Forward Selection は、特徴量を1つずつ追加しながらモデルの性能を高めていく手法で、どの特徴量が最も効果的かを順に見極めたいときに有効です。
- 一方、Backward Elimination は、すべての特徴量からスタートし、不要な特徴量を段階的に削除していくことで、モデルをシンプルに保ちつつ精度を維持できます。
どちらの手法も、scikit-learnの交差検証とスコアリング機能を活用することで、 客観的な指標に基づいた特徴量選定が可能になります。
最適な特徴量セットを見つけることで、モデルの精度向上だけでなく、解釈性や計算効率の向上にもつながるので、 ぜひ自分のデータでも試してみてください。









コメント