「Python実践】欲しい信号を見つけ出せ! ウェーブレット変換を使った3つの応用例~ノイズ除去・異常検知・時間周波数解析~」の記事では、ウェーブレット変換の基礎と、スカログラム(ヒートマップ)を使った「目視による異常検知」のアプローチを紹介しました。
今回はそこから一歩進んで、「システムによる自動監視」の実装に焦点を当てます。 具体的には、異常を機械的に判定するための閾値(しきいち)の設定アルゴリズムと、高感度な検知につきものの「誤検知(オオカミ少年)問題」をどう防ぐか、その実践的な解決策を解説していきます。

ウェーブレットを使った異常検知
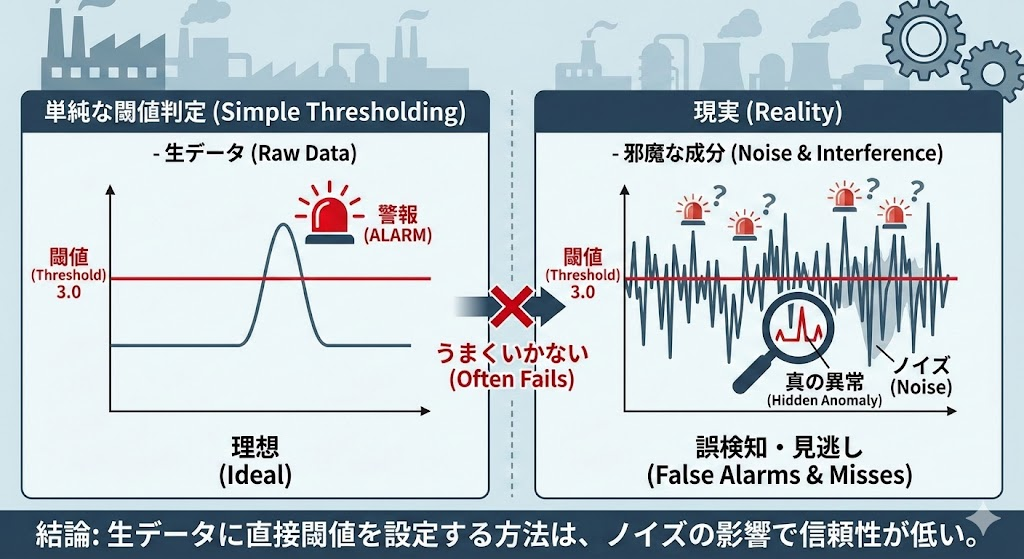
工場やIoTの現場において、異常検知の最初のアプローチとしてよく使われるのは、「センサーの値が 3.0 を超えたら警報を鳴らす」といった単純な閾値(しきいち)判定です。 しかし、生データ(Raw Data)に対して直接閾値を設定する方法は、多くの場合うまくいきません。なぜなら、現場のデータには「邪魔な成分」が混ざっているからです。
- ベースの振動: 正常稼働しているモーターの揺れ(サイン波など)
- 環境ノイズ: 電源由来のノイズや、周囲の振動
- ドリフト: 温度変化などで、データの基準点(オフセット)がゆっくりズレていく現象
これらが混ざった状態で閾値を設定しようとすると、正常な振動の「山」を異常と誤判定したり、逆にドリフトのせいで異常を見逃したりします。
そこでウェーブレット変換の出番です。 ウェーブレット変換を使えば、データを周波数(スケール)ごとに分解できます。これにより、「低周波の振動(正常)」と「高周波のスパイク(異常)」を綺麗に分離し、異常成分だけをまな板の上に載せることができるのです。
異常検知を自動化するには
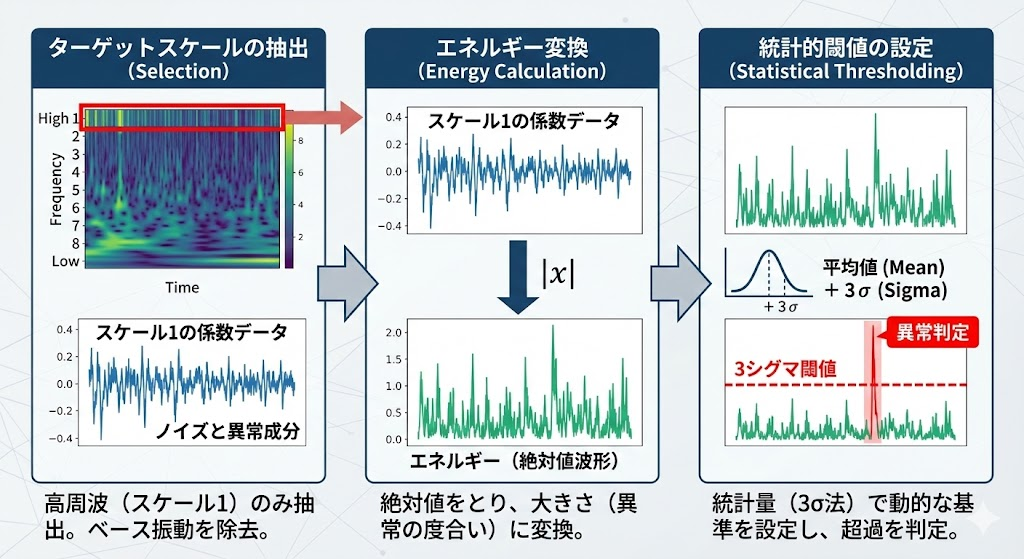
前回の記事で紹介した「スカログラム(ヒートマップ)」は、人間がデータ全体を俯瞰するには最適ですが、コンピュータによる自動監視にはデータ量が多すぎます。 自動化システムを作るには、以下の3ステップで「監視すべき数値を一本化」します。
異常(衝撃やスパイク)は、一瞬の鋭い変化です。これはウェーブレット変換の世界では「スケールが小さい(高周波)領域」に強く現れます。 そこで、ヒートマップ全体を見るのではなく、「スケール1(最も細かい波)」の係数データだけを抽出します。 この時点で、ベースの振動(低周波)は除去され、ノイズと異常成分だけが残ります。
ウェーブレット係数はプラスとマイナスの値を激しく行き来します。大きさ(異常の度合い)を評価しやすくするために、絶対値をとって「エネルギー」に変換します。
ここで初めて閾値を設定します。ただし、「3.0」のような固定値ではなく、データの統計量を使います。 一般的には3シグマ法(平均値 + 3 × 標準偏差)を使います。これにより、「普段のノイズレベルならこれくらい収まるはず」という基準を動的に引き、そこからはみ出したものを「異常」と判定します。
実装方法
前回のイメージ図で解説した「3つのステップ(ターゲット抽出・エネルギー変換・統計的閾値)」を、そのままPythonコードに実装しました。
現場での分析業務を想定し、単なる計算実験ではなく、CSVデータの読み込みやPandas(データフレーム)との連携を含めた、実務で使える構成にしています。
このコードのポイント
- 現場に近いデータフロー
センサーデータをCSVとして保存し、Pandasで読み込んで処理するという、実際のIoT分析に近い流れを再現しました。 - ロジックの関数化
detect_anomalies関数の中に「ウェーブレット変換 → エネルギー化 → 3シグマ判定」の処理をまとめています。 - 劇的なBefore/After
グラフの上段(生データ)ではノイズに埋もれて見えない異常が、下段(解析結果)では「そこだけ」が反応して閾値を超えている様子が明確に分かります。 - マザーウェーブレットにキシカンハット(mexh)を使用
メキシカンハットは、突発的な変化の抽出に特化しているため、今回はこれを利用しました。
以下が実装のサンプルプログラムです。テストデータの生成も含んでいますので、実行すると結果が確認できます。
テストデータ、異常検知、グラフ化はそれぞれコピペしやすいように関数化しています。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import pywt
import os
plt.rcParams['font.family'] = 'MS Gothic'
# ---------------------------------------------------------
# 1. テストデータ作成 & CSV保存関数
# ---------------------------------------------------------
def create_test_data_and_save_csv(filename='sensor_data.csv'):
"""
異常検知テスト用の疑似データを作成し、CSVとして保存する。
"""
np.random.seed(42)
t = np.linspace(0, 1, 400)
# 正常な振動(低周波) + ノイズ
normal_signal = np.sin(2 * np.pi * 5 * t)
noise = np.random.normal(0, 0.3, len(t))
data = normal_signal + noise
# ★異常を混入(0.5秒地点 index=200 に鋭いスパイク)
data[200] += 4.0
# DataFrame化
df = pd.DataFrame({
'time': t,
'value': data
})
# CSV保存 (indexは保存しない)
df.to_csv(filename, index=False)
print(f"[Info] テストデータを保存しました: {filename}")
# ---------------------------------------------------------
# 2. 異常検知関数 (DataFrame対応版)
# ---------------------------------------------------------
def detect_anomalies(df, target_column, wavelet='mexh', scale=1, sigma_n=3):
"""
DataFrameの指定カラムに対してウェーブレット変換を行い、異常を検知する。
Args:
df (pd.DataFrame): 解析対象のデータフレーム
target_column (str): 解析するカラム名
wavelet (str): マザーウェーブレットの種類 (default: 'mexh')
scale (int): 抽出するスケール (default: 1, 高周波・スパイク狙い)
sigma_n (float): 閾値を決める際の標準偏差の倍率 (default: 3)
Returns:
dict: 解析結果が入った辞書
- 'energy': ウェーブレット係数のエネルギー(絶対値)
- 'threshold': 計算された閾値
- 'anomaly_indices': 閾値を超えたインデックスのリスト
"""
# データ取り出し
data = df[target_column].values
# (A) ウェーブレット変換
# scalesはリストで渡す必要がある
coefs, freqs = pywt.cwt(data, [scale], wavelet)
# (B) ターゲット抽出 & エネルギー変換
# coefsは [スケール数, データ長] の形状なので、index 0 を取得
target_coef = coefs[0]
energy = np.abs(target_coef)
# (C) 統計的閾値の決定(3シグマ法)
mean = np.mean(energy)
std = np.std(energy)
threshold = mean + sigma_n * std
# (D) 判定 (閾値を超えたインデックスを取得)
anomaly_indices = np.where(energy > threshold)[0]
return {
'energy': energy,
'threshold': threshold,
'anomaly_indices': anomaly_indices
}
# ---------------------------------------------------------
# 3. グラフ描画関数
# ---------------------------------------------------------
def plot_results(df, target_column, result_dict):
"""
元データと異常検知結果をグラフに描画する。
"""
data = df[target_column].values
energy = result_dict['energy']
threshold = result_dict['threshold']
anomalies = result_dict['anomaly_indices']
fig, axes = plt.subplots(2, 1, figsize=(10, 8), sharex=True)
# 上段:生データ
axes[0].plot(data, color='gray', label='観測データ (Raw)')
axes[0].set_title(f'元データ: {target_column} (ノイズにより異常が見えにくい)')
axes[0].axhline(3.0, color='green', linestyle='--', label='固定閾値の例 (3.0)')
axes[0].legend()
axes[0].grid(True)
# 下段:解析結果
axes[1].plot(energy, color='blue', label='ウェーブレットエネルギー (解析値)')
axes[1].set_title('解析結果: ノイズが除去され、異常だけが反応')
axes[1].axhline(threshold, color='red', linestyle='--', label=f'動的閾値 (Mean + 3σ): {threshold:.2f}')
# 異常箇所のプロット
if len(anomalies) > 0:
axes[1].scatter(anomalies, energy[anomalies], color='red', s=100, zorder=5, label='検知箇所')
print(f"[Result] 異常検知インデックス: {anomalies}")
else:
print("[Result] 異常は検知されませんでした。")
axes[1].legend()
axes[1].grid(True)
plt.tight_layout()
plt.show()
# =========================================================
# メイン実行ブロック
# =========================================================
if __name__ == "__main__":
CSV_FILE = 'factory_sensor_log.csv'
TARGET_COL = 'value'
# 1. データの準備(CSV作成)
create_test_data_and_save_csv(CSV_FILE)
# 2. データの読み込み(Pandas)
if os.path.exists(CSV_FILE):
df_sensor = pd.read_csv(CSV_FILE)
print(f"[Info] データを読み込みました。行数: {len(df_sensor)}")
# 3. 異常検知の実行
# 引数にDataFrameとカラム名を渡すだけでOK
results = detect_anomalies(df_sensor, TARGET_COL)
# 4. 結果の可視化
plot_results(df_sensor, TARGET_COL, results)
else:
print("CSVファイルが見つかりません。")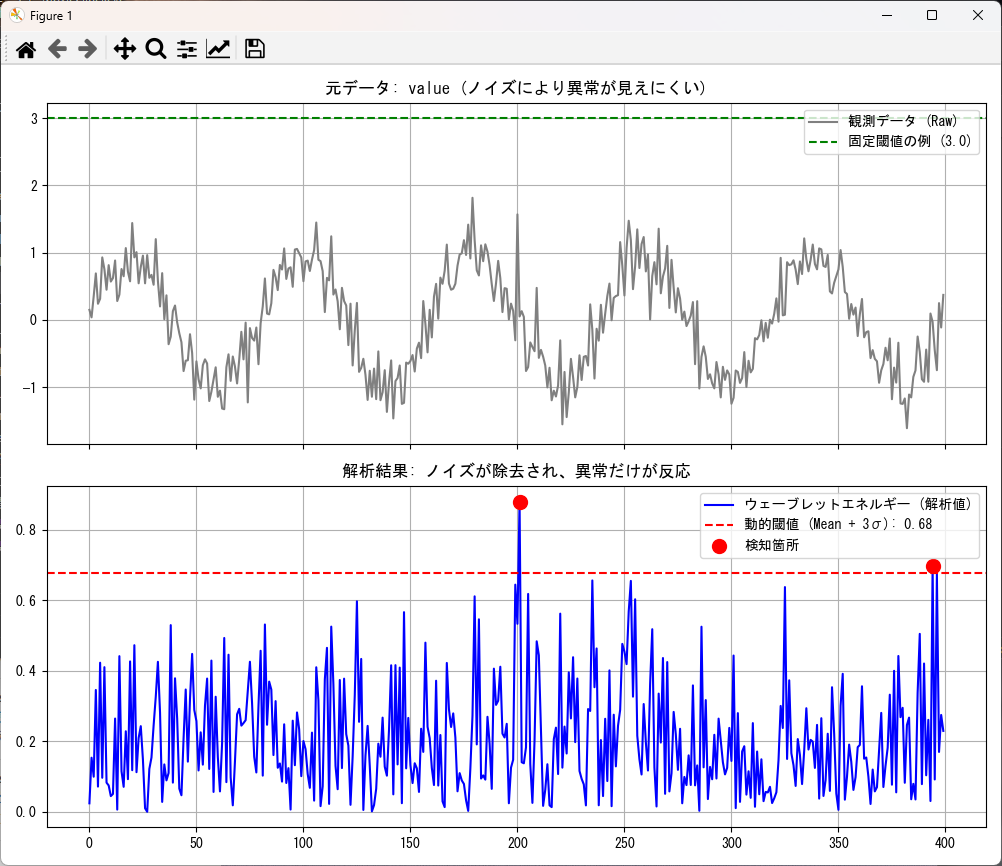
上段:元データによる閾値判定
上のグラフ(灰色)は、センサーから取得した生データを模しています。 ここには、正常な振動(サイン波)と環境ノイズに加え、中央(200ms地点)に「異常な衝撃(スパイク)」を意図的に混入させています。
しかし、この異常信号の強さはあえて小さく設定しており、グラフ上の見た目は周囲のノイズとほとんど区別がつきません。 図中の緑色の点線(値=3.0)は、一般的な警報システムで設定される「固定閾値」の例です。ご覧の通り、異常が発生しているにもかかわらず、信号は閾値に届いていません。つまり、従来の手法ではこの異常は「正常」として見逃されてしまいます。
下段:ウェーブレット変換による「可視化」
下のグラフ(青色)は、同じデータに対してウェーブレット変換(CWT)を行い、そのエネルギー量をプロットしたものです。劇的な違いが一目瞭然です。
- ノイズの除去: 周囲のランダムなノイズや、ゆっくりとした正常な振動成分は、解析によって値が低く抑えられています。
- 異常の強調: 埋もれていた「異常な衝撃」だけが、鋭い周波数成分の変化として捉えられ、中央で鋭いピークを描いています。
一見すると正常に見えるデータの中にも、故障の予兆となる微細な変化は隠れています。ウェーブレット変換のような時間周波数解析を用いることで、S/N比(信号対雑音比)が悪い過酷な環境下でも、確度の高い異常検知が可能になります。
2枚目の画像の下段、右端(index 400付近)にも小さな反応がありますが、以下の理由でよく発生します。
境界効果(Edge Effect)
ウェーブレット変換などの信号処理では、データの「端っこ」で計算が不安定になり、値が跳ねることがあります。
偶然のノイズ
ランダムノイズの中に、たまたま異常波形に近い「鋭い動き」が含まれていた可能性があります(統計的閾値なので、確率的に数%は誤検知が出ることがあります)。
実務では、端っこのデータを無視したり、数回連続で検知したらアラートを出す、といった工夫でこれを回避します。
まとめ
今回の記事では、従来の閾値判定では見逃してしまう「ノイズに埋もれた微弱な異常」を、ウェーブレット変換を用いて明確に検知できることを実証しました。
単にデータの「大きさ(振幅)」を見るのではなく、その裏にある「波形の変化」を捉えるこの手法は、AI学習の前処理や、設備の故障を未然に防ぐ予兆保全において強力な武器となります。
ぜひ、皆さんの現場にある「使い道がない」と諦めていたデータでもこのアプローチを試し、新たな知見を発掘してみてください。








コメント