センサーデータや振動解析を行っていると、必ずぶつかる壁があります。
「ノイズが酷くて、肝心の信号が見えない」 「FFT(フーリエ変換)をかけたけれど、いつ異常が起きたのか時間がわからない」
そんな時こそ、ウェーブレット変換の出番です。 ウェーブレット変換は、複雑な信号から欲しい波形を見つけ出す強力な手法であり、これ一つで「ノイズ除去」「異常検知」「時間周波数解析」が可能になります。
しかし、いざPythonで実装しようとすると、「どの波形(マザーウェーブレット)を選べばいいの?」と迷ってしまいがちです。
そこで本記事では、実務で頻出するこれら3つの応用パターンに絞り、それぞれの目的に最適な「波形の選び方」と「Python実装コード」をセットで解説します。
泥だらけのデータから、あなたの欲しい信号を見つけ出しましょう!
そもそも「ウェーブレット」とは?
「ウェーブレット変換」という名前はよく聞きますが、そもそも「ウェーブレット(Wavelet)」とはどういう意味でしょうか?
実は、Waveとlet とい2つの単語が合体した言葉です。
- Wave(波)
- let(小さい) ※booklet(小冊子)、piglet(子豚)などと同じ接尾辞
つまり、直訳すると「さざなみ(小さい波)」という意味です。
では、私たちがよく知っている「サイン波(フーリエ変換の主役)」は、過去から未来まで、ずっと同じリズムで振動し続けるのに対し、ウェーブレット(Wavelet)は、ゼロから始まり、少し振動して、すぐにまたゼロに戻ります。
言い換えると、サイン波は「永遠に続く波」であり、ウエーブレットは「瞬間的な波」になります。
「ウェーブレット変換」とは
ウェーブレット変換は、この「瞬間的な波」をセンサーデータ上で走らせることで、「『いつ』『どの周波数が』発生していたか」を把握するための分析手法」です。
- フーリエ変換:
「この曲には『ド』と『ミ』と『ソ』の音が使われている」までは分かるが、どの順番で演奏されたか(メロディ)は分からない。 - ウェーブレット変換:
「楽譜」のように、「開始5秒地点で『ド』が鳴り、10秒地点で『ミ』が鳴った」という、時間と周波数の両方の情報が得られる。
どうやって分析しているの?(仕組みのイメージ)
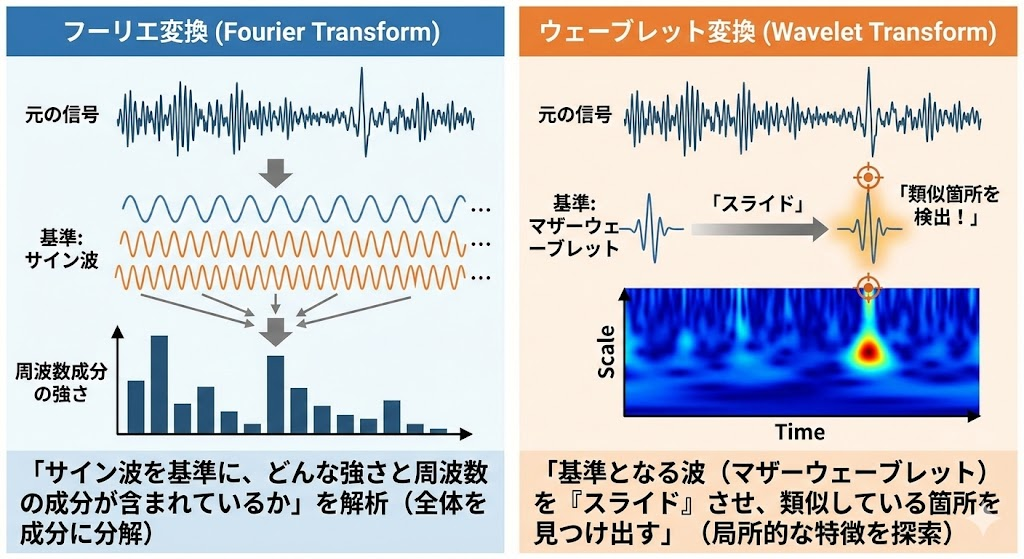
フーリエ変換は「サイン波を基準に、どんな強さと周波数の成分が含まれているか」を解析するのに対し、ウェーブレット変換は「基準となる波(マザーウェーブレット)と類似している箇所を見つけ出す」手法と言えます。
具体的には、あらかじめ「検出したい波の形(マザーウェーブレット)」を決めておき、それを元の信号に重ね合わせて「スライド」と「伸縮」を繰り返します。
- マザーウェーブレット(型の決定)
基本となる「小さな波の形」を決めます(メキシカンハット型やモルレー型など)。 - スライド(時間の特定)
この小さな波を、信号の最初から最後までずらしながら「波形が似ているか(相関)」をチェックします。似ている場所が見つかれば、「いつ(時刻)」その変動が起きたかが分かります。 - スケール(周波数の特定)
次に、この小さな波を横に引き伸ばしたり(低周波用)、縮めたり(高周波用)して、また最初からスライドさせます。どの幅の波にマッチしたかで、「どの周波数か」が特定できます。
つまり、「いつ(スライド位置)」、「どのくらいの速さの変動が(スケール)」起きたのかを同時に特定できるのです。
マザーウェーブレットの決め方は?
ここで問題になるのは、どうやって基本となるマザーウェーブレットを決めるかです。
実は、ウェーブレット変換には「これを使えばOK」という万能な波形はありません。選定の基本ルールは非常にシンプルで、「見つけたい異常や特徴に、一番『形』が似ているものを選ぶ」ことです。
これは「型はめパズル」と同じ原理です。 たとえば、トゲのような鋭いスパイクノイズを見つけたいなら、同じように尖った形をした波形(メキシカンハットなど)を使います。逆に、周期的な揺らぎを見たいなら、波打った形(モルレーなど)を使います。 ターゲットの形に似ている波を選ぶことで、他の成分に惑わされず、その特徴だけを感度よく検出できるようになるのです。
「小さな波の形」を考える場合、数学的には多くの種類が存在しますが、実務での異常検知において「最初に試すべき波形」はある程度決まっています。迷った場合は、以下の基準で選んでみてください。
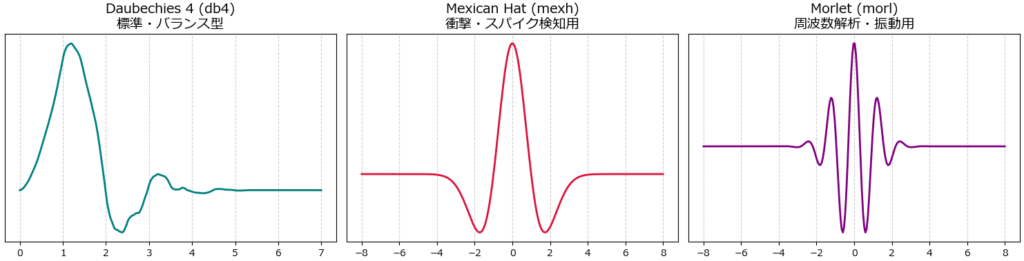
- Daubechies 4 (db4): 最も汎用的な「標準レンズ」のような存在。振動データに含まれるノイズ除去や、一般的な異常検知なら、まずはこれから試すのが鉄則です。
- Mexican Hat (メキシカンハット): 「帽子」のような形をした波形。一瞬の衝撃(スパイク)や、突発的な変化点を見つけるのに特化しています。
- Morlet (モルレー): サイン波に近い形状。フーリエ変換のように「周波数の変化」を滑らかに見たい場合に最適です。
何に使えるの?(メリット)
特に「突発的な変化」や「ノイズ除去」に非常に強いです。
- 異常検知
ずっと一定の振動をしていた機械が、「ガツン!」と一瞬だけ衝撃を受けた場合、フーリエ変換ではその一瞬の変化が埋もれてしまいますが、ウェーブレット変換なら「この瞬間に高周波の衝撃があった」とピンポイントで検出できます。 - ノイズ除去
信号の形(トレンド)は残したまま、細かいギザギザ(高周波ノイズ)だけをきれいに取り除くことができます。 - 画像圧縮
JPEG 2000などの画像圧縮技術にも使われています。
ウェーブレット変換を使ったノイズ除去
センサーデータのノイズ除去といえば、移動平均やローパスフィルタを使ってノイズをならす方法が多く使われます。しかし、この方法には致命的な副作用があります。それは、ノイズを消すと同時に、信号の急激な変化(エッジ)まで「なまって」しまうことです。
例えば、機械が故障した瞬間の「ガクッ」という急変化こそが重要な異常サインなのに、フィルタをかけることでその特徴がぼやけて見えなくなってしまうのです。
一方、ウェーブレット変換(DWT) は、アプローチが根本的に異なります。 信号を「低周波(大まかな形)」と「高周波(細かい変動)」に分解し、「信号の鋭い立ち上がり(エッジ)はそのまま残しつつ、不要な細かいノイズだけをピンポイントで削除する(閾値処理)」 ことが可能です。
これにより、データの「鮮度」を保ったまま、分析しやすいクリーンな波形を手に入れることができます。
ノイズ除去の手順
ウェーブレット変換を使ったノイズ除去は、以下の3つのステップで行われます。
- 分解(Decomposition)
信号を「低周波(近似成分)」と「高周波(詳細成分)」の2つに分けます。 - 選別(Thresholding)
高周波成分(詳細成分)に含まれる細かいギザギザのうち、「ある大きさ(閾値)以下のもの」はただのノイズとみなして捨てます。 - 再構成(Reconstruction)
残った「重要な成分」だけを繋ぎ合わせて、元の形に戻します。
Pythonでこの処理を行うには、デファクトスタンダードであるライブラリ PyWavelets (pywt) を使用します。
実装において最も重要なのが、「どのマザーウェーブレット(波形の型)を使うか」という選択です。今回は、位相のズレ(波形のタイミングのズレ)を最小限に抑えるために、以下の設定を使用します。
- ライブラリ:
PyWavelets - マザーウェーブレット:
sym4(Symlets 4)
下記が具体的なサンプルプログラムです。
import numpy as np
import matplotlib.pyplot as plt
import pywt
# 日本語フォント設定(環境に合わせて変更してください)
plt.rcParams['font.family'] = 'Meiryo'
def generate_test_data(duration=1.0, points=400, freq=5, noise_std=0.3):
"""
テスト用のノイズ付きデータを生成する関数
"""
t = np.linspace(0, duration, points)
signal = np.sin(2 * np.pi * freq * t) # 正解の信号
noise = np.random.normal(0, noise_std, len(t)) # ノイズ
data = signal + noise # 観測データ(入力)
return t, signal, data
def wavelet_denoising(data, wavelet='sym4', level=2):
"""
ウェーブレット変換によるノイズ除去を行う関数
"""
# 1. 分解(Decomposition)
coeffs = pywt.wavedec(data, wavelet, level=level)
# 2. 閾値(Threshold)の計算
# 中央値絶対偏差 (MAD) を用いてノイズレベルを推定
sigma = np.median(np.abs(coeffs[-1])) / 0.6745
threshold = sigma * np.sqrt(2 * np.log(len(data)))
# 3. 閾値処理(詳細成分のみをソフト閾値処理し、近似成分 coeffs[0] はそのまま残す)
new_coeffs = [coeffs[0]] + [pywt.threshold(c, threshold, mode='soft') for c in coeffs[1:]]
# 4. 再構成(Reconstruction)
return pywt.waverec(new_coeffs, wavelet)
def plot_results(t, original, noisy, denoised, title='【ノイズ除去】 ウェーブレット変換結果'):
"""
結果を比較描画する関数
"""
plt.figure(figsize=(10, 6))
# ノイズありデータ
plt.plot(t, noisy, color='lightgray', label='入力データ(ノイズあり)')
# 除去後データ
plt.plot(t, denoised, color='red', linewidth=2, label='除去後 (Denoised)')
# 正解データ
plt.plot(t, original, color='blue', linestyle='--', alpha=0.5, label='正解データ (Ground Truth)')
plt.title(title)
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')
plt.legend()
plt.grid(True, alpha=0.5)
plt.tight_layout()
plt.show()
if __name__ == "__main__":
# 1. データの準備
t, signal, data = generate_test_data()
# 2. ノイズ除去の実行
# wavelet='sym4' (シンレット) は波形をきれいに保ちやすいため推奨
denoised_data = wavelet_denoising(data, wavelet='sym4', level=2)
# 3. 結果の描画
plot_results(t, signal, data, denoised_data, title='【ノイズ除去】 sym4によるデノイズ結果')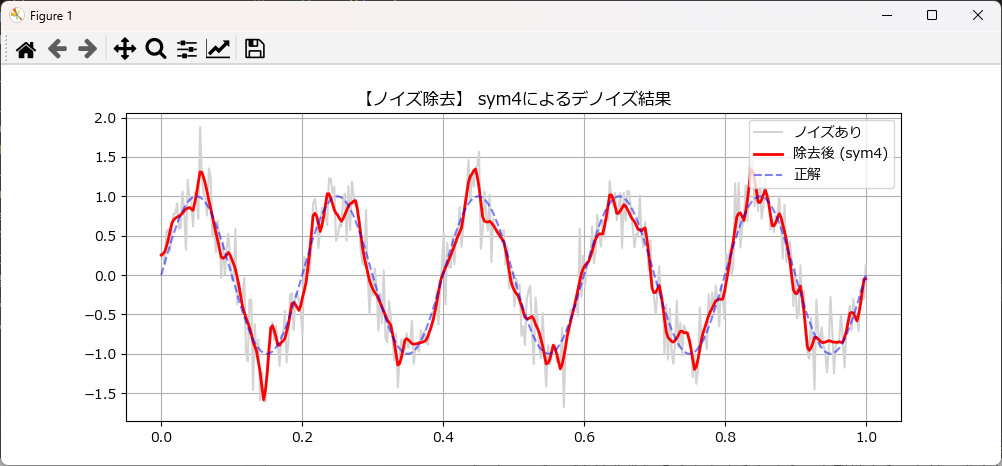
ウェーブレット変換を使った異常検知
工場の設備監視などでは、ベアリングの欠けやギアの破損などが発する「一瞬の衝撃(スパイク)」を検知する必要があります。
しかし、現場のデータは常にノイズを含んでいます。単純に「振幅が〇〇を超えたら異常」という閾値(しきいち)判定では、ノイズレベルが高いと、小さな異常兆候を見逃してしまうか、逆にノイズを異常と誤検知してしまいます。
ここで役に立つのが、信号の「大きさ」ではなく「形」に着目するアプローチです。
異常信号(衝撃波)には特有の「尖った形」があります。ウェーブレット変換(CWT)を使えば、データの波形の中から「異常信号と同じ形をしている部分」だけを浮かび上がらせることができます。 これは、いわば「ウォーリーを探せ」のように、特定のパターン(形)を探し出す処理(パターンマッチング)と言えます。
異常検知の手順
ウェーブレット変換を使った異常検知は、以下の3つのステップで行われます。
- テンプレート選定(Template Selection)
探したい異常(衝撃やスパイク)と「形が似ている波形」を選びます。今回は、突発的な衝撃にそっくりなmexh(メキシカンハット)を使います。 - スキャンと伸縮(Scanning & Scaling)
選んだ波形をデータの上で「スライド(時間移動)」させながら、同時に波の幅を「伸縮(スケール変化)」させます。これにより、「いつ起きたか?」だけでなく「どのくらいの鋭さ(幅)か?」まで網羅的に探索します。 - 類似度の判定(Detection)
波形がピタリと重なった部分は、計算結果(係数)が大きくなります。これをヒートマップなどで可視化し、「色が濃くなっている場所=異常」として特定します。
このプロセスにより、ノイズに埋もれて人間の目では見えないような微弱な異常でも、数学的な「形の類似度」を使って浮き彫りにすることができるのです。
Pythonでこの処理を行うには、デファクトスタンダードであるライブラリ PyWavelets (pywt) を使用します。
異常検知の実装において最も重要なのが、「探したい異常の形に似ているマザーウェーブレットを選ぶ」という点です。今回は、突発的な衝撃(スパイク)を感度よく捉えるために、以下の設定を使用します。
- ライブラリ:
PyWavelets - マザーウェーブレット:
mexh(Mexican Hat / メキシカンハット)- 選定理由: その名の通り「帽子」のように中心が鋭く尖った形をしており、検出したい異常波形(衝撃スパイク)と形状が非常に似ているため、パターンマッチングに最適だからです。
import numpy as np
import matplotlib.pyplot as plt
import pywt
# 日本語フォント設定
plt.rcParams['font.family'] = 'Meiryo'
def generate_anomaly_data(duration=1.0, sampling_rate=400, noise_std=0.4):
"""
1. データ作成:
正弦波に強いノイズを加え、特定箇所に異常(スパイク)を埋め込みます。
"""
np.random.seed(42)
t = np.linspace(0, duration, sampling_rate)
# ベースの信号(5Hzのサイン波) + ノイズ
signal = np.sin(2 * np.pi * 5 * t)
noise = np.random.normal(0, noise_std, len(t))
data = signal + noise
# ★異常(衝撃)を埋め込む
# 真ん中あたり(index=200)に鋭いスパイクを追加
anomaly_idx = int(sampling_rate / 2)
data[anomaly_idx] += 3.0
return t, data
def analyze_signal_cwt(data, wavelet='mexh', scale_range=(1, 11)):
"""
2. データ解析(異常検知):
CWT(連続ウェーブレット変換)を行い、時間周波数解析の結果を返します。
※元のコードは「ノイズ除去」ではなく「パターンマッチングによる検出」を行っています。
"""
scales = np.arange(scale_range[0], scale_range[1])
coefs, freqs = pywt.cwt(data, scales, wavelet)
return coefs, scales
def plot_cwt_results(t, data, coefs, scales):
"""
3. グラフ描画:
元データとスカログラム(解析結果)を表示します。
"""
fig, axes = plt.subplots(2, 1, figsize=(10, 6), sharex=True)
# 上段:元データ
axes[0].plot(t, data, color='gray')
axes[0].set_title('観測データ(ノイズが強くて、異常がどこにあるか分かりにくい)')
axes[0].set_ylabel('振幅')
axes[0].grid(True)
# 下段:解析結果(ヒートマップ)
# extent=[xmin, xmax, ymin, ymax] を設定して軸を合わせる
extent = [t[0], t[-1], scales[0], scales[-1]]
# 係数の絶対値を表示
im = axes[1].imshow(np.abs(coefs), aspect='auto', cmap='jet', extent=extent, origin='lower')
axes[1].set_title('解析結果(スカログラム):中央の「赤色」が衝撃の発生箇所!')
axes[1].set_ylabel('スケール(波の幅)')
axes[1].set_xlabel('時間 [s]')
fig.colorbar(im, ax=axes[1], label='類似度')
plt.tight_layout()
plt.show()
# --- メイン処理 ---
if __name__ == "__main__":
# 1. データの準備
t, data = generate_anomaly_data()
# 2. 解析の実行(CWT)
coefs, scales = analyze_signal_cwt(data)
# 3. 結果の可視化
plot_cwt_results(t, data, coefs, scales)プログラムを実行すると、下記グラフが作成されます。
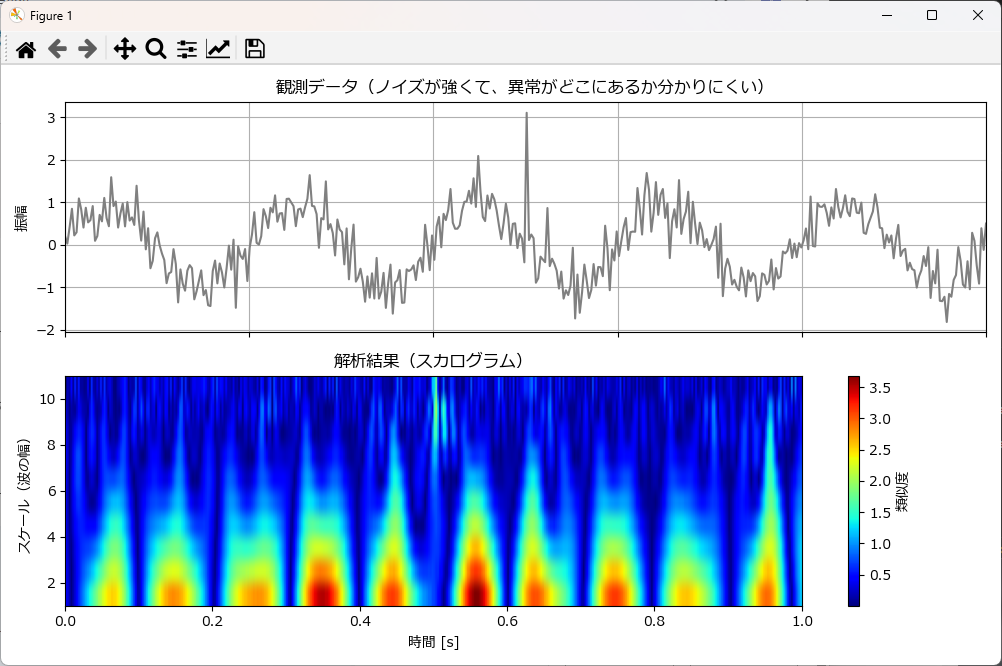
グラフ上段
「ノイズが乗った元のデータ」です。
全体がギザギザしているため、「どこで衝撃(異常)が起きたのか」を目視で判断するのは非常に困難です。パッと見では、ただの乱れた波にしか見えません。
グラフ下段
「解析結果(スカログラム)」です。
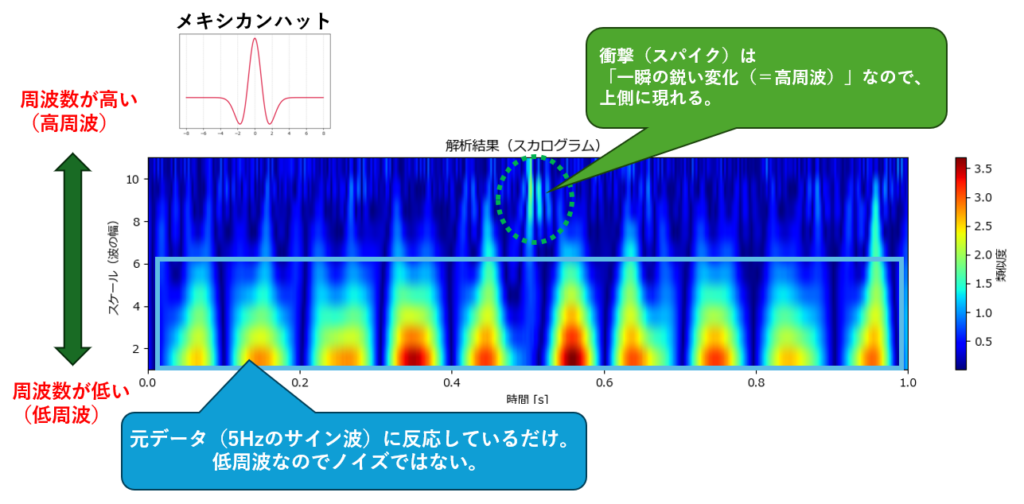
ウェーブレット変換によって、「メキシカンハット(異常の形)」との類似度を色で表したヒートマップ(スカログラム)です。
横軸は時間を、縦軸はスケール(探している波の幅=周波数の高さ)を表しています。
グラフ中央(0.5秒付近)の上(緑の点線で囲っている部分)を見てください。ここがスパイク異常の箇所です。
スパイクは周波数が高いので、グラフの上に表示されます。一方下には複数で類似度が高い(赤色)箇所がいくつもありますが、これは元データ(低周波のサイン波)に反応しているだけで、異常ではありません。
ウェーブレット変換を使って自動的に異常を検出するには、データを「代表値」に変換し、統計的に判断するプロセスが必要です。 具体的なPythonコードと実装手順については、「【Python実践】ウェーブレット変換で実用「異常検知」~閾値設定から誤検知対策まで~」の記事で詳しく解説しています。

ウェーブレット変換を使った時間周波数解析
最後は、ウェーブレット変換の真骨頂である「周波数の移り変わり」の解析です。 例えば、モーターの回転数が徐々に上がっていく音や、人の話し声のような「時間とともに周波数が変化するデータ」は、通常のFFT(フーリエ変換)ではうまく扱えません(「高い音と低い音が混ざっている」という結果しか出ないため)。
ウェーブレット変換を使えば、これを「楽譜」のように可視化できます。
時間周波数解析
可視化において最も重要なのは、人間が見て直感的に分かりやすい波形を選ぶことです。ここでは、解析の「標準レンズ」とも言える morl を使用します。
理由は、形が「サイン波」に一番近く、フーリエ変換(周波数解析)と同じ感覚で結果を解釈できるからです。「周波数」と「時間」のバランスが良く、データの全体像を掴むスカログラム(可視化)描画において最もスタンダードな波形です。
- ライブラリ:
PyWavelets - マザーウェーブレット:
morl(Morlet / モルレー)
import numpy as np
import matplotlib.pyplot as plt
import pywt
# 日本語フォント設定
plt.rcParams['font.family'] = 'Meiryo'
def generate_chirp_data(duration=1.0, sampling_rate=400, freq_factor=30):
"""
1. データ作成:
チャープ信号(時間が経つにつれて振動が速くなる波形)を生成します。
sin(2 * pi * f * t^2) の形により、周波数がリニアに変化します。
"""
t = np.linspace(0, duration, sampling_rate)
# tの2乗に比例させることで、徐々に周波数が上がる
chirp_signal = np.sin(2 * np.pi * freq_factor * t**2)
return t, chirp_signal
def analyze_signal_cwt(data, wavelet='morl', max_scale=64):
"""
2. 解析実行:
Morletウェーブレットを用いてCWTを行います。
scalesは 1 から max_scale までの範囲で解析します。
"""
scales = np.arange(1, max_scale)
coefs, freqs = pywt.cwt(data, scales, wavelet)
return coefs, scales
def plot_cwt_results(t, data, coefs, scales):
"""
3. 結果の描画:
元データとスカログラムを表示します。
周波数の推移(スイープ)が視覚的にわかるようにします。
"""
fig, axes = plt.subplots(2, 1, figsize=(10, 8), sharex=True)
# 上段:元データ
axes[0].plot(t, data)
axes[0].set_title('元データ(右に行くほど振動が速くなっている)')
axes[0].set_ylabel('振幅')
axes[0].grid(True)
# 下段:解析結果(スカログラム)
# imshowのextentを設定して、軸の数値を物理的な意味(時間、スケール)に合わせます。
# [xmin, xmax, ymin, ymax]
# ここでは ymin=scales[-1](大きいスケール=低周波), ymax=scales[0](小さいスケール=高周波)
# とすることで、Y軸の上に行くほど「高周波(細かい波)」になるように表示しています。
extent = [t[0], t[-1], scales[-1], scales[0]]
axes[1].imshow(np.abs(coefs), aspect='auto', cmap='inferno', extent=extent)
axes[1].set_title('解析結果:右に行くにつれて「スケール」が小さくなっている(=周波数が高くなっている)')
axes[1].set_ylabel('スケール (小さいほど高周波)')
axes[1].set_xlabel('時間 [s]')
plt.tight_layout()
plt.show()
# --- メイン処理 ---
if __name__ == "__main__":
# 1. データ作成
t, chirp_signal = generate_chirp_data()
# 2. 解析実行
coefs, scales = analyze_signal_cwt(chirp_signal)
# 3. 結果描画
plot_cwt_results(t, chirp_signal, coefs, scales)プログラムを実行すると、下記グラフが作成されます。
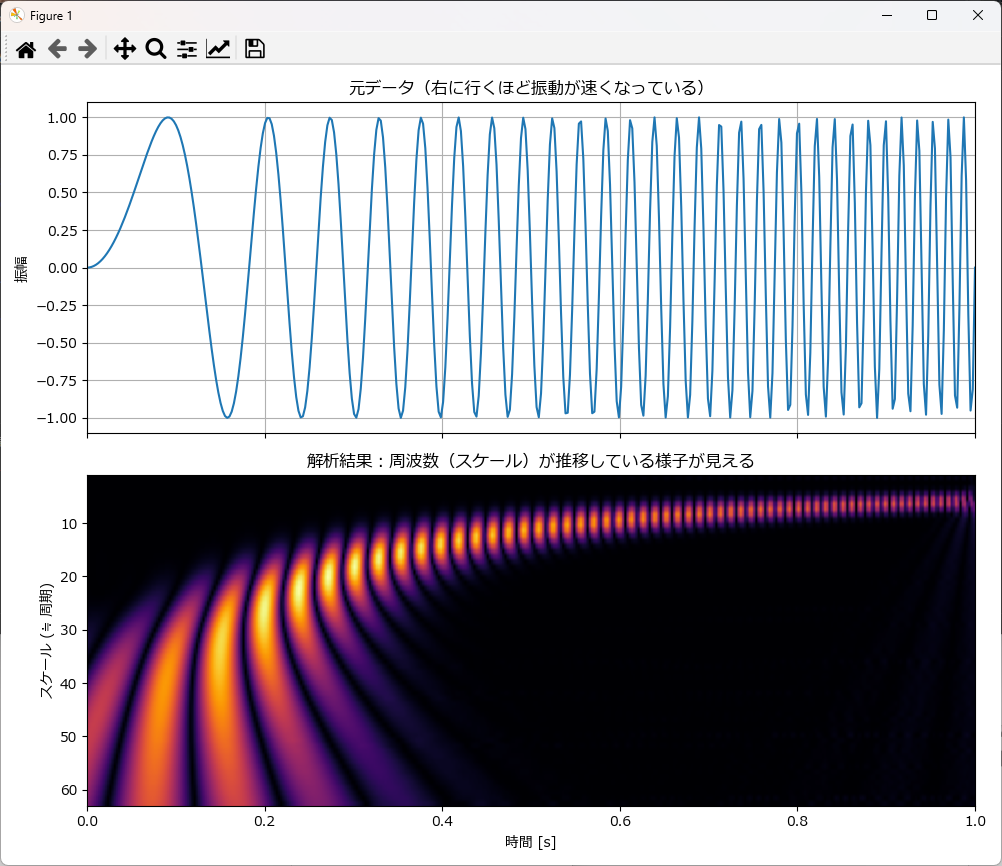
この図は、徐々に周波数が上がっていく「チャープ信号」を解析した結果です。 単に「周波数が上がっている」だけでなく、ウェーブレット変換特有の「精度(解像度)の変化」が見て取れます。
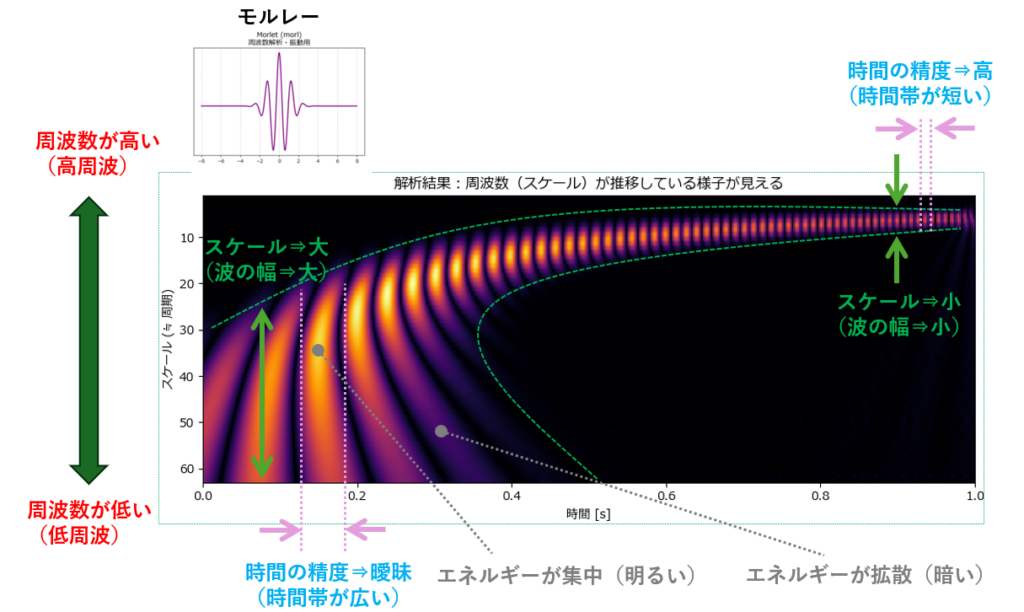
1. 縦軸のルール:スケールと周波数
図の左側にある緑の矢印に注目してください。
- 下に行くほど(スケール大): 低周波(ゆったりした波)を表します。
- 上に行くほど(スケール小): 高周波(細かい波)を表します。
2. 「扇形」に歪む理由(時間の精度の違い)
解析結果の赤い帯が、直線ではなく「扇形(カーブ)」を描いている点、そして「帯の太さ」が変わっている点(ピンクと水色の点線部分)が最大のポイントです。
- 【左下】低周波のとき(波が大きい)
波長が長いため、波を捉えるのに長い時間が必要です。そのため、横方向(時間)にボヤッと広がり、「いつ発生したか」の精度は少し甘く(曖昧に)なります。 - 【右上】高周波のとき(波が小さい)
波長が短いため、一瞬の変化も逃さず捉えられます。そのため、横方向(時間)にシュッと細くなり、「いつ発生したか」の精度が非常に高くなります。
3. 明るさ(エネルギー)の変化
グレーの点線が示すように、最初は色が濃く(明るく)、後半につれて少し薄く(暗く)なっています。 これは、高周波になるほど成分が縦方向(周波数方向)に拡散しやすくなるため、エネルギーの密度が見かけ上薄まっているためです。
この図が示す通り、ウェーブレット変換は「低い音は全体像をゆったり捉え、高い音は一瞬の変化を鋭く捉える」という、人間の耳に近い自然な聞こえ方を可視化しています。
まとめ
本記事では、ウェーブレット変換を使った3つのアプローチを紹介しました。 重要なのは、「ウェーブレット変換」という単一の魔法があるわけではないということです。目的に応じて、適切な「マザーウェーブレット(波の形)」と「手法(DWTかCWTか)」を選ぶことで、初めてその真価を発揮します。
| 目的 | 手法 | 推奨ウェーブレット | 選定理由 | キーワード |
|---|---|---|---|---|
| ① ノイズ除去 | 離散 (DWT) | sym4 | 左右対称性が高く、波形のズレ(位相歪み)を防げるため | エッジ保存、閾値処理 |
| ② 異常検知 | 連続 (CWT) | mexh | 衝撃(スパイク)の形状に似ており、感度よく反応するため | パターンマッチング |
| ③ 可視化 | 連続 (CWT) | morl | サイン波に近く、周波数(Hz)として直感的に理解しやすいため | スペクトログラム、不確定性原理 |
フーリエ変換(FFT)は強力ですが、「時間」の情報が消えてしまうという弱点がありました。 ウェーブレット変換は、その弱点を克服し、「いつ、何が起きたか」を教えてくれる強力な顕微鏡です。
- データが汚いなら、まずは
sym4で磨く。 - 異常を見つけたいなら、
mexhでスキャンする。 - 変化を見たいなら、
morlで地図を描く。
この3つの「初期装備」さえ覚えておけば、泥だらけのセンサーデータの中から、あなたの探している「欲しい信号」が見つかります。 ぜひ、紹介したPythonコードをコピーして、手持ちのデータで試してみてください!








コメント