サポートベクターマシン(SVM)は、機械学習における強力なアルゴリズムの一つであり、分類問題や回帰問題、さらには異常検知にも幅広く利用されています。
特に少ないデータでも高い精度を出せる点が特徴で、ビジネスや研究の現場で重宝されています。
本記事では、SVMの基本概念から仕組み、具体的な使い方までを、Pythonを使ったサンプルコードも交えながら解説します。PythonをでSVMを実践したくなったら、是非参考にしてください。
ポートベクターマシン(SVM)とは何か?
サポートベクターマシン(SVM)は、教師あり学習の一種で、データを特定のクラスに分類するアルゴリズムです。高次元のデータでも有効で、分類だけでなく回帰や異常検知といったさまざまな応用が可能です。
SVMの強みは、「マージン」と呼ばれる分類境界の幅を最大化することで、より汎化性能の高いモデルを構築できる点にあります。
サポートベクターマシンの基本概念
SVMの基本概念は、「データを境界線で分ける」というシンプルな考え方に基づいています。しかし、SVMが他のアルゴリズムと異なるのは、分類境界(決定境界)だけでなく、その境界から最も近いデータ点(サポートベクター)との距離を最大化する点です。この距離(マージン)を広くとることで、データが少し変動しても正確に分類できる頑健なモデルが完成します。
また、SVMでは単純な直線(線形分離)だけでなく、「カーネル法」と呼ばれる手法を使って、非線形なデータも分類可能です。これにより、複雑なデータセットでも高精度な分類が可能になります。
SVMの目的
SVMの目的は、分類問題や回帰問題を高精度で解くことです。具体的には、次のような場面で活用されます。
- 分類問題: 画像認識、テキスト分類、異常検知など
- 回帰問題: 数値予測やトレンド分析
- 異常検知: 異常データを検出して不正や故障を見つける
SVMは特に次のような特徴を持つデータセットに適しています。
- サンプル数が少ない
- 特徴量が多く高次元
- データが線形分離可能、または少しの工夫で分離可能
SVMの仕組み(マージン最大化とサポートベクター)
SVMのコアとなる考え方は、「マージンの最大化」です。
- 決定境界の作成:
SVMは、異なるクラスのデータを分ける境界線(ハイパープレーン)を作成します。 - サポートベクターの選定:
境界線に最も近いデータ点をサポートベクターと呼びます。このサポートベクターが決定境界を決定する重要な役割を果たします。 - マージンの最大化:
SVMは、サポートベクターと決定境界の距離を最大化するように学習を行います。これにより、分類の確実性が高まります。
非線形データに対しては、「カーネル関数」を使うことで、データを高次元空間にマッピングし、線形で分類可能な状態に変換します。代表的なカーネル関数には以下のようなものがあります。
- 線形カーネル:
データが線形分離可能な場合に使用 - 多項式カーネル:
曲線的なデータに対応 - RBF(ガウス)カーネル:
最も一般的で、複雑なデータに対応可能
このようにして、SVMは高精度な分類・回帰・異常検知を実現します。
サポートベクターマシンの用途
SVMは幅広い用途で使用されますが、主に以下の3つが代表的です。
分類問題
SVMは、画像認識、テキスト分類、スパムメール検出など、さまざまな分類タスクで使われます。たとえば、手書き数字認識では各数字を分類するためにSVMが活用されます。SVMの強みは、高次元データでも効果的に分類できる点です。
回帰問題(SVR)
SVMは回帰問題にも応用されます。この場合、サポートベクターマシン回帰(Support Vector Regression, SVR)として知られ、数値の予測やトレンド分析などに使われます。SVRは、外れ値の影響を受けにくく、精度の高い予測が可能です。
異常検知(One-Class SVM)
SVMは異常検知にも利用されます。特にOne-Class SVMは、通常のデータをモデル化し、そこから外れたデータを異常と判断します。製造業における機器の故障検知や、不正アクセスの検出などで活用されます。
サポートベクターマシンのメリットとデメリット
メリット
- 高次元データに強い:
SVMは次元数が多いデータに対しても適切に動作します。高次元データでは、データポイントが疎になる傾向があるため、SVMのマージン最大化が有効に働くことが多いためです。しかし、高次元データは計算コストが非常に高くことになるため、特徴量選択や次元削減を行うことが一般的です。 - マージン最大化による汎化性能が高い:
SVMはマージン(クラス間の境界から最も近いデータ点までの距離)を最大化することで、未知のデータに対して高い精度で予測できます。また、過学習を防ぐメカニズムが組み込まれており、モデルの安定性が高いです。 - カーネルトリックにより複雑な非線形問題にも対応:
カーネルトリックを使うことで、データを高次元空間にマッピングし、線形で分離できない問題も解決可能です。例えば、円や複雑な曲線で分けられるデータも適切に分類できます。 - 少量データ(数千件以下)でも有効:
サンプル数が少なくても効果的に学習できます。逆に、大規模データセット(数十万件以上)の場合、ランダムフォレストやXGBoost、ニューラルネットワークなどがより効率的です。
デメリット
- 大規模データセットには不向:
SVMの計算量はデータ数の2乗または3乗に比例するため、大規模データセットでは学習時間が非常に長くなる可能性があります。
例えば、数十万以上のデータセットでは、ランダムフォレストやニューラルネットワークの方が効率的な場合があります。 - ハイパーパラメータ調整が必要:
カーネルの種類やC(コストパラメータ)、γ(ガンマ)などのハイパーパラメータ調整が困難です。
また、不適切なパラメータ設定では過学習や未学習を引き起こします。 - 結果の解釈が難しい:
線形SVMはある程度解釈可能ですが、非線形カーネル(特にRBFカーネルなど)を使用した場合は、モデルの内部がブラックボックス化し、解釈が困難になります。 - ノイズに敏感:
ソフトマージン(Cの調整)である程度対応可能ですが、データのクリーニングが重要です。
ラベルの誤りや外れ値がある場合、境界が大きく影響を受けることがあります。 - 異なるスケールのデータに弱い:
異なるスケールを持つ特徴量が存在する場合、大きなスケールの特徴量がモデルの決定境界に不適切に影響を与える可能性が生じます。この場合、標準化(平均が0、標準偏差が1になるよう調整)や正規化(各特徴量が0~1の間に収まるよう調整)が不可欠です。
SVMが適するデータ、適さないデータ
SVMは高次元・少量データに強く、クラス間の境界がはっきりしている場合に最適です。逆に大規模データや外れ値が含まれるデータには弱いので、データを十分に見極める必要があります。
SVMが適しているデータ
- 高次元で特徴量が多いが、データ量が少ない場合:
特徴量(次元)が多く、データのサンプル数が少ない場合はSVMが有効です。
遺伝子データの様な数千の遺伝子情報(高次元)がありつつ、サンプル数が限られる場合によく用いられます。製造業においては遺伝子ほどではありませんが、設備のセンサーデータがこれに該当します。
テキスト分類においては、各文章が数千次元のベクトル(TF-IDFなど)として表されるものの、サンプルの数は数百から数千程度にとどまるケースにも有効です。 - ククラス間の境界がはっきりしているデータ:
SVMはクラス間のマージンを最大化することが目的であり、明確に分離できるデータであれば非常に高い精度を発揮します。例えば、犬と猫の分類など、生物種やカテゴリがはっきりしているデータはSVMの得意領域です。 - 少量のデータでも高精度を期待したい場合:
SVMは少数のデータでも高精度な分類が可能です。データが少なくてもサポートベクター(境界近くのデータポイント)だけを利用して学習するため、無駄なデータに依存せず、効率的に境界を見つけられます。
SVMが適さないデータ
- データ数が非常に多い場合:
数十万件以上の大規模データセットでは、SVMの学習に膨大な時間がかかります。
特にカーネル法を使用する場合、全データの組み合わせを計算により元データの2乗~3乗の計算量が必要になります。大規模データの場合は、LinearSVM(線形SVM)、ランダムフォレスト、XGBoostなど他の手法が推奨されます。 - クラスが重なっているデータ:
クラス間でデータが大きく重なっている場合、SVMは適切な境界を引くのが難しくなります。
SVMはマージンを最大化する手法であり、クラスが曖昧で交差していると、誤分類が増加します。
この場合は、ロジスティック回帰やランダムフォレストの方が精度が向上する可能性があります。 - 外れ値が多いデータ:
SVMは外れ値に非常に敏感です。外れ値が多い場合、学習時に外れ値も境界を決定する要素となり、モデルの精度が低下します。外れ値がある場合は、前処理で外れ値を除去しておくか、ソフトマージンSVM(正則化項を調整して外れ値を無視する)を利用する、あるいは外れ値の影響を受けにくいランダムフォレストやロジスティック回帰を選択します。 - リアルタイム性が求められる場合:
SVMは学習に時間がかかるため、リアルタイム処理が必要なアプリケーションには不向きです。推論(予測)は非常に高速ですが、モデルの再学習が必要な場合はSVMは効率的ではありません。
リアルタイム性が求められる場合は、決定木ベースのアルゴリズムやニューラルネットワークの方が優れています。
サポートベクターマシンの基本的な使い方
SVMは2種類存在し、データを直線で分離できる場合には線形SVMを、曲線でしか分類できない場合は非線形SVM(カーネル法)を使用します。
線形SVMの使い方
線形SVMは、データが線形に分離可能である場合に使用します。データが線形に分離可能とは、データを1本の直線(または高次元空間では平面や超平面)で分割できる状態です。
SVMは高次元の分類を得意としていますが、4次元以上は可視化ができないため、下記のサンプルでは4つに分類可能な特徴量を2個(2次元データ)持つデータを分類/可視化しています。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
# サンプルデータの生成(4種類に分類可能な2次元のデータを100個生成)
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, n_classes=4, random_state=42)
# データを訓練用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 線形SVMモデルの作成
linear_svm = SVC(kernel='linear', C=1)
# モデルの訓練
linear_svm.fit(X_train, y_train)
# テストデータで予測
y_pred = linear_svm.predict(X_test)
# 精度の評価
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy * 100:.2f}%")
# グラフの描画
def plot_decision_boundary(X, y, model):
h = .02 # メッシュステップサイズ
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolor='k', s=20)
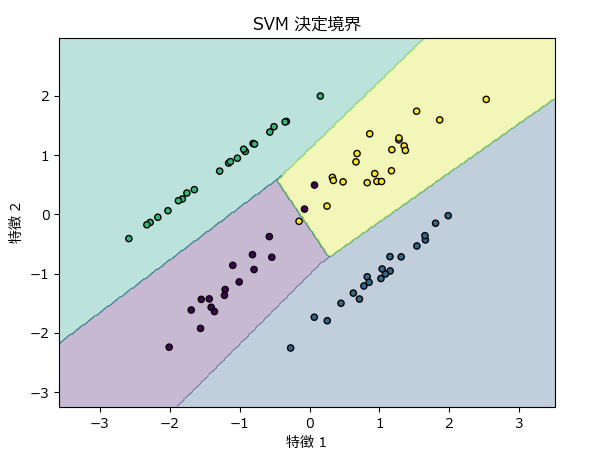
plt.title("SVM 決定境界")
plt.xlabel("特徴 1")
plt.ylabel("特徴 2")
plt.show()
# 訓練データと決定境界の描画
plot_decision_boundary(X_train, y_train, linear_svm)
Accuracy: 100.00%
主要なハイパーパラメータ
| パラメータ | 説明 |
|---|---|
| C | 誤分類をどれだけ許容するかを決めるパラメータです。Cが大きいと、誤分類を許さず、モデルがデータにフィットしようと強くなり、過学習のリスクが高くなります。Cが小さいと、誤分類を許容し、一般化能力が高くなる傾向があります。 |
非線形SVM(カーネル法)の使い方
データが線形に分離できない場合、SVMにカーネル法を使うことで、非線形な境界を学習することができます。カーネル法は、入力データを高次元空間にマッピングし、その空間で線形SVMを適用することで、非線形の問題を線形に解く手法です。SVCクラスでは、以下のようなカーネルを選択できます。
- 線形カーネル (
kernel='linear') - 多項式カーネル (
kernel='poly') - RBFカーネル(ガウスカーネル) (
kernel='rbf') - シグモイドカーネル (
kernel='sigmoid')
下記は、非線形SVMの代表的なカーネルであるRBFカーネルを使用したコード例です。可視化しないのであれば高次元のデータをそのまま分類できますが、下記サンプルでは3次元グラフを描画したかったので、4つに分類可能な特徴量を2個(2次元データ)持つデータを分類/可視化しています。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.svm import SVC
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
# サンプルデータの生成 (3種類に分類可能な3次元データを100個生成)
X, y = make_classification(n_samples=100, n_features=3, n_informative=3, n_redundant=0, n_repeated=0, n_classes=3, random_state=42)
# データを訓練用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 非線形SVM(RBFカーネル)の使用
rbf_svm = SVC(kernel='rbf', C=1, gamma=0.5)
# モデルの訓練
rbf_svm.fit(X_train, y_train)
# テストデータで予測
y_pred_rbf = rbf_svm.predict(X_test)
# 精度の評価
accuracy_rbf = accuracy_score(y_test, y_pred_rbf)
print(f"Accuracy (RBF Kernel): {accuracy_rbf * 100:.2f}%")
# 3Dプロットの描画
def plot_decision_boundary_3d(X, y, model):
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
z_min, z_max = X[:, 2].min() - 1, X[:, 2].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 50), np.linspace(y_min, y_max, 50))
zz = np.zeros(xx.shape)
for i in range(xx.shape[0]):
for j in range(xx.shape[1]):
zz[i, j] = model.predict(np.array([[xx[i, j], yy[i, j], 0]]))[0]
ax.plot_surface(xx, yy, zz, alpha=0.3, rstride=100, cstride=100)
scatter = ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y, edgecolor='k', s=20)
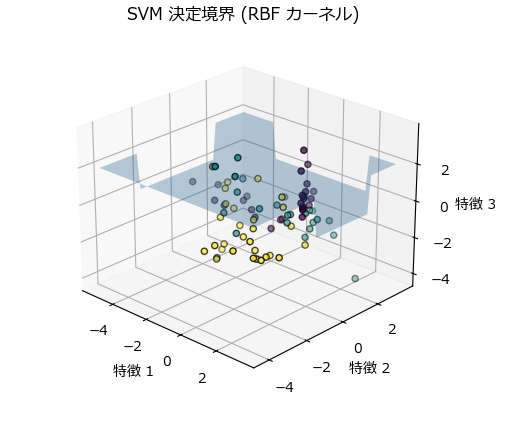
ax.set_title("SVM 決定境界 (RBF カーネル)")
ax.set_xlabel("特徴 1")
ax.set_ylabel("特徴 2")
ax.set_zlabel("特徴 3")
plt.show()
# 3次元データと決定境界の描画
plot_decision_boundary_3d(X_train, y_train, rbf_svm)
Accuracy (RBF Kernel): 75.00%
RBFカーネルのパラメータ
| パラメータ | 説明 |
|---|---|
| C | 線形SVMと同様に、Cは誤分類の許容度を0.1~1000などの範囲で調整します。 小さい値 (例 0.1):柔軟なモデルを作成し、過学習(オーバーフィッティング)を防ぎます。 大きい値 (例 1000) :データに厳密にフィットさせたモデルを作成します。 大きな値の場合、誤分類を減らすためにモデルがより複雑になり、過学習のリスクが高まります。 |
| γ(ガンマ) | γはカーネルの広がり具合を制御するパラメータで、0.0001~10などの範囲で調整します。 小さい値 (例 0.0001) :より広い領域を考慮し、境界が滑らかになります。 大きい値 (例 10):局所的な領域にフィットし、境界が鋭くなります。 γが大きいと、データポイントが近くにある場合に強い影響を与え、過学習を引き起こす可能性があります。逆に、γが小さいと、データ全体に対して広範囲に影響を与え、モデルが簡素化され、過学習を防ぐことができます。 |
特徴量が4以上(高次元)のデータに対する可視化
高次元のデータを可視化する場合は、次元削減にて2次元又は3次元に変換しなければなりません。
下記サンプルは、PCAを使って2次元データに変換し、そのデータを非線形SVMにて分類、可視化しています。
但し、次元削減することは、多少なりともデータが劣化(分類精度が低下)することは避けられません。「【Python実践】データ分析の影の立役者!主成分分析(PCA)の使い方ガイド(コピペで使えるサンプルコード付き)」の記載内容を参考に、寄与率が最低でも70%以上であることを確認しておきましょう。
もし精度を重視するなら、次元削減後のグラフは説明用の参考資料に留め、実際の分類は高次元データで作成したモデルを使用するのが良いと思います。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.decomposition import PCA
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
# サンプルデータの生成(4種類に分類可能な100次元のデータを200個生成)
X, y = make_classification(n_samples=200, n_features=100, n_informative=4, n_redundant=0, n_clusters_per_class=1, n_classes=4, random_state=42)
# データを訓練用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# PCAによる次元削減(100次元を2次元に削減)
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train)
X_test_pca = pca.transform(X_test)
# 非線形SVM(RBFカーネル)の使用
rbf_svm_pca = SVC(kernel='rbf', C=1, gamma=0.5)
# 次元削減後のデータを使ってモデルの訓練
rbf_svm_pca.fit(X_train_pca, y_train)
# テストデータで予測
y_pred_rbf_pca = rbf_svm_pca.predict(X_test_pca)
# 精度の評価
accuracy_rbf_pca = accuracy_score(y_test, y_pred_rbf_pca)
print(f"Accuracy (RBF Kernel, PCA): {accuracy_rbf_pca * 100:.2f}%")
# グラフの描画
def plot_decision_boundary(X, y, model):
h = .02 # メッシュステップサイズ
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolor='k', s=20)
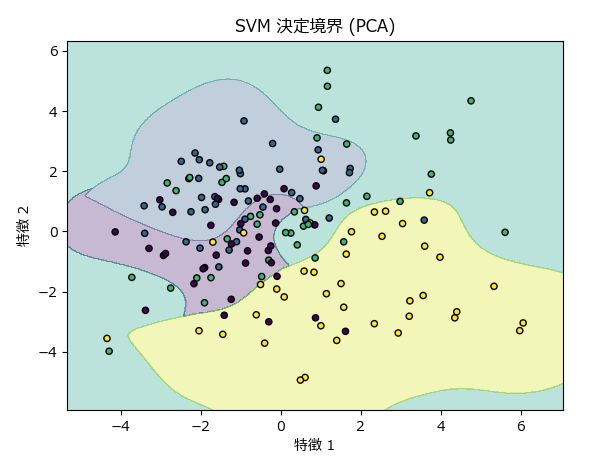
plt.title("SVM 決定境界 (PCA)")
plt.xlabel("特徴 1")
plt.ylabel("特徴 2")
plt.show()
# PCAで次元削減したデータで決定境界の描画
plot_decision_boundary(X_train_pca, y_train, rbf_svm_pca)Accuracy (RBF Kernel, PCA): 62.50%
SVMの結果の解釈の仕方
SVMの分類結果を解釈する方法として、次の3つがあります。
サポートベクターの可視化
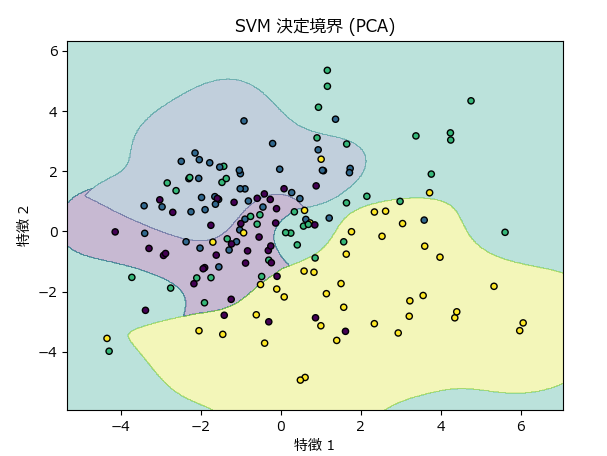
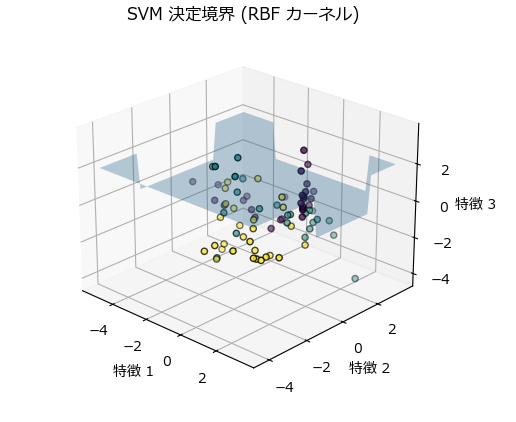
これまでに紹介したサンプルプログラムの通り、2次元又は3次元データとしてグラフ化することで、各データポイントがどのように分類されているかを把握できます。
決定境界の解釈
決定境界は、異なるクラスのデータポイントを分けるための境界です。線形SVMの場合、決定境界は直線または平面であり、単純な形状を持ちます。
非線形SVM(RBFカーネルなど)の場合、 決定境界は複雑な曲面となり、データの分布に応じた形状をとります。
分類精度
分類精度は、テストデータに対してモデルがどれだけ正確に分類できるかを示します。
ここまでに紹介したサンプルプログラムでは、accuracy_score(全体の予測のうち正しく分類された割合=正確率)だけを計算していました。
accuracy_scoreだけで事足りる場合も少なくありませんが、それ以外にも重要な評価し行があります。
「【Python実践】機械学習による分類モデルの予測精度を定量的に評価する [Accuracy,Precision,Recall,F1,ROC](コピペで使えるサンプルコード付き)」に各指標の詳しい説明と、コピペで使えるサンプルプログラム、自作の便利関数を公開していますので参考にしてください。
例えば、evaluate_classification_metrics()を使うと、簡単に複数の評価を得ることができます。
# ~ 省略 ~
evaluate_classification_metrics(y_test, y_pred_rbf_pca)正確度 (Accuracy): 62.50%
クラス 0 - 適合率 (Precision): 0.62, 再現率 (Recall): 0.71, F1スコア: 0.67
クラス 1 - 適合率 (Precision): 0.45, 再現率 (Recall): 0.71, F1スコア: 0.56
クラス 2 - 適合率 (Precision): 1.00, 再現率 (Recall): 0.45, F1スコア: 0.62
クラス 3 - 適合率 (Precision): 0.62, 再現率 (Recall): 0.62, F1スコア: 0.62
混同行列:
[[10 4 0 0]
[ 2 5 0 0]
[ 1 2 5 3]
[ 3 0 0 5]]
過学習の判断方法
過学習の判定は、モデル訓練時の精度とテストデータの精度を比較し、モデル訓練時の精度が過度に高いかを確認することで判定できますが、学習曲線(ROC曲線)を描くことで、視覚的に理解することができます。
「【Python実践】機械学習による分類モデルの予測精度を定量的に評価する [Accuracy,Precision,Recall,F1,ROC](コピペで使えるサンプルコード付き)」に具体的なサンプルプログラムを公開していますので、併せてご確認ください。2値分類と多値分類では少しプログラムが異なりますので、ご注意ください。
下記は2値のROC曲線のサンプルです。
# ~ 省略 ~
# 非線形SVM(RBFカーネル)の使用( probability=Trueを指定)
rbf_svm_pca = SVC(kernel='rbf', C=1, gamma=0.5, probability=True)
# ~ 省略 ~
# 陽性クラスの予測確率を取得(0列目:クラス0の確率、1列目:クラス1の確率が格納されている)
y_prob = rbf_svm_pca.predict_proba(X_test_pca)[:, 1]
# ROC曲線のプロット(2値)
plot_roc_curve(y_test, y_prob)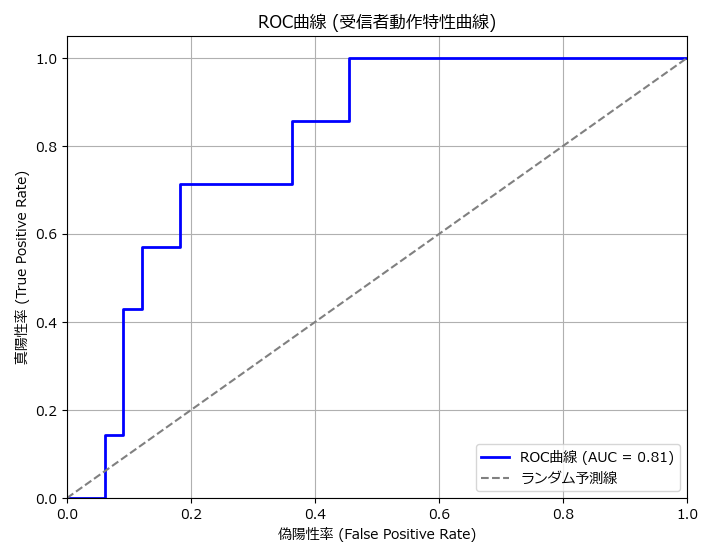
下記は多値のROC曲線のサンプルです。
# ~ 省略 ~
# 非線形SVM(RBFカーネル)の使用( probability=Trueを指定)
rbf_svm_pca = SVC(kernel='rbf', C=1, gamma=0.5, probability=True)
# ~ 省略 ~
# 陽性クラスの予測確率を取得
y_prob = rbf_svm_pca.predict_proba(X_test_pca)
# ROC曲線のプロット(多値)
plot_roc_curve_multi(y_test, y_prob)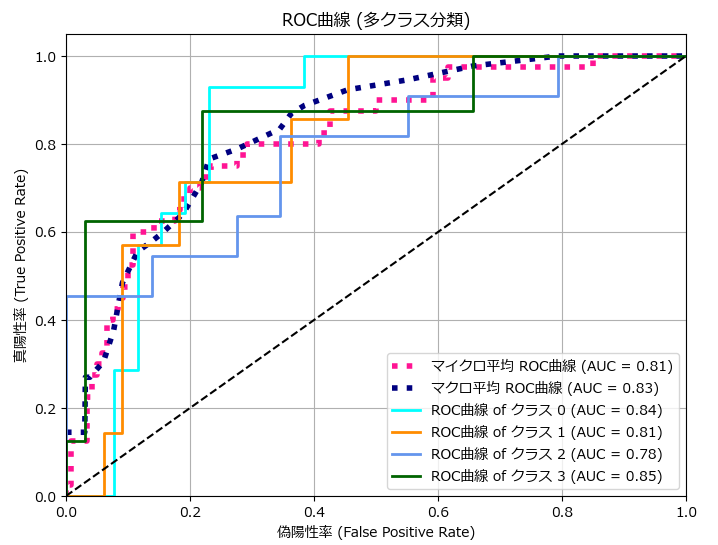
最適なハイパーパラメータを求める
最適なハイパーパラメータを求める方法として、グリッドサーチがあります。下記は多クラス分類におけるハイパーパラメータをグリッドサーチで求めるサンプルです。
import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
# サンプルデータの生成(多クラス分類、特徴量50)
X, y = make_classification(n_samples=1000, n_features=50, n_informative=30, n_redundant=10, n_classes=3, random_state=42)
# SVMモデルの設定
svm = SVC()
# パラメータグリッドの設定
param_grid = {
'C': [0.1, 1, 10, 100, 1000],
'gamma': [1, 0.1, 0.01, 0.001, 0.0001],
'kernel': ['rbf']
}
# グリッドサーチの設定
grid = GridSearchCV(svm, param_grid, refit=True, verbose=3)
grid.fit(X, y)
# 最適なパラメータの表示
print("Best Parameters:", grid.best_params_)
# グリッドサーチ後の最適モデルを取得
best_model = grid.best_estimator_
print("Best Model:", best_model)

サポートベクターマシンを使う上での注意点
サポートベクターマシン(SVM)は、分類問題や回帰問題で強力なパフォーマンスを発揮する機械学習アルゴリズムです。しかし、その効果を最大限に引き出すためには、いくつかの重要なポイントに注意する必要があります。
スケーリング
SVMは、特徴量のスケールに敏感なアルゴリズムであるため、あらかじめ特徴量のスケールを確認し、必要に応じて標準化(Standardization)や正規化(Normalization)を行います。
特徴量選択と次元削減
SVMは、高次元データが得意とはいうものの、計算量が多いことからパフォーマンスに影響を与えます。計算量を削減する方法として、特徴量選択と次元削減が重要です。
- 特徴量選択
特徴量の中から有用なものを選び出すことで、不要な特徴量を排除します。これにより、モデルの複雑さが減り、過学習のリスクが低減します。- フィルタ法: 各特徴量の統計的特性に基づいて選択します(例:相関係数、分散分析)。
- ラッパー法: モデルの性能を評価しながら特徴量を選択します(例:逐次特徴選択法)。
- 組み込み法: モデルの訓練過程で特徴量を選択します(例:LASSO)。
- 次元削減
データの次元を減らす手法で、PCA(主成分分析)が代表的です。次元削減により、データの冗長性を減らし、計算効率が向上します。
SVMによる回帰問題(SVR)
回帰問題は、連続値を予測するタスクです。サポートベクター回帰(Support Vector Regression=SVR)は、サポートベクターマシンを回帰に適用したもので、連続的な目標変数を予測するために使用されます。
SVMの代わりにSVRに置き換えることで、回帰問題に対応できます。
from sklearn.svm import SVR
svr = SVR(kernel='rbf', C=値, gamma=値)
回帰問題の予測結果を評価する方法は「【Python実践】機械学習による回帰モデルの予測精度を定量的に評価する [MAE,MSE,RMSE,R2](コピペで使えるサンプルコード付き)」の記事に記載しています。
import matplotlib.pyplot as plt
from sklearn.svm import SVR
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
from matplotlib import rcParams
# 日本語フォントの設定
rcParams['font.family'] = 'Meiryo'
# サンプルデータの生成(回帰問題、特徴量50)
X, y = make_regression(n_samples=200, n_features=50, noise=0.1, random_state=42)
# データを訓練用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 最適なパラメータを使用してSVRモデルを再訓練
svr = SVR(kernel='rbf', C=100, gamma=0.01)
svr.fit(X_train, y_train)
# テストデータで予測
y_pred = svr.predict(X_test)
# 精度の評価
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f"Mean Squared Error: {mse:.2f}")
print(f"R^2 Score: {r2:.2f}")
# 結果のプロット
plt.figure(figsize=(8, 6))
plt.scatter(y_test, y_pred, color='blue', label='予測値 vs 実測値')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=2, label='理想的な直線')
plt.xlabel('実測値')
plt.ylabel('予測値')
plt.title('SVRによる回帰')
plt.legend()
plt.grid()
plt.show()Mean Squared Error: 2139.63
R^2 Score: 0.82
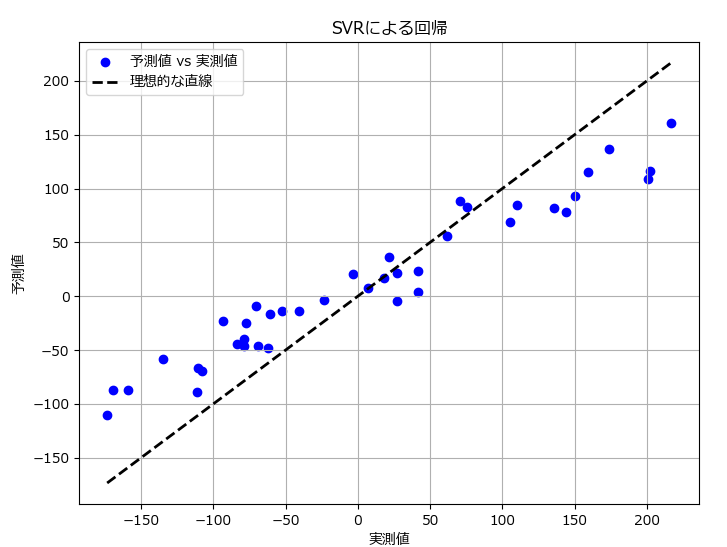
SVMによる異常検知(One Class SVM)
SVMを異常検知に特化したものがOne-Class SVM(One-Class Support Vector Machine)です。One-Class SVMは、通常のSVMと同様にマージン最大化の概念を使用しますが、主に正常なデータを学習し、異常なデータを検出するために設計されています。
詳しくは、「【Python実践】OneClassSVMで異常検知を行う(コピペで使えるサンプルコード付き)」の記事で紹介しています。
SVMが簡単に行える自作クラス
SVMによる分類と可視化が簡単に実行できるSVMUtilクラスと、グラフを描画するための plot_svm_results_2d()、plot_svm_results_1d()関数を作成しました。
使い方は下記のサンプルを参考にしてください。
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# ここにSVMUtilとグラフ描画関数のコードを張り付けるか、インポートしてください
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
import numpy as np
import pandas as pd
# ------------------------------------------------------------------
# 訓練データを生成し、DataFrameに変換
# ------------------------------------------------------------------
# シードを固定
np.random.seed(42)
# ダミーデータの生成
data = {
'feature1': np.random.rand(100),
'feature2': np.random.rand(100),
'target': np.random.choice([0, 1], size=100)
}
df = pd.DataFrame(data)
# ------------------------------------------------------------------
# 生成した訓練データでSVMを学習し、モデルを保存
# ------------------------------------------------------------------
# SVMUtilクラスのインスタンスを作成
svm_util = SVMUtil(df)
# モデルを学習する
svm_util.fit(column=['feature1', 'feature2'], target='target', C=1.0, gamma='scale', kernel='rbf')
# 予測を行う
predictions = svm_util.predict(column=['feature1', 'feature2'])
print(predictions)
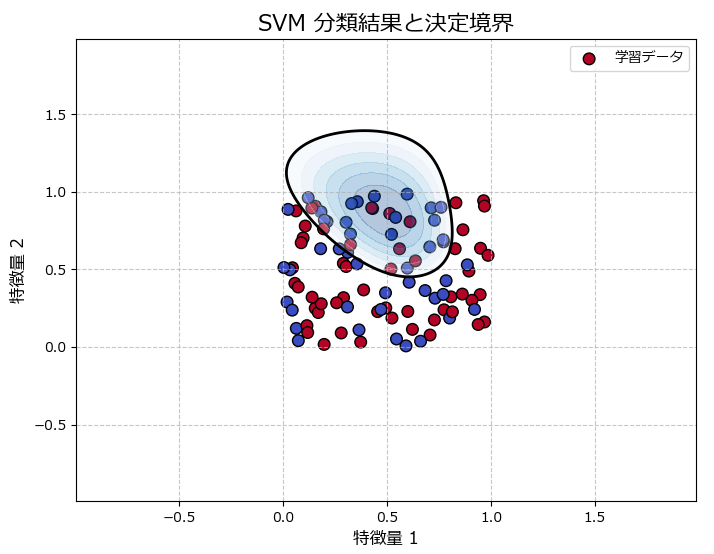
# 訓練データの分類結果をグラフ化
plot_svm_results_2d(svm_util,X_train=df[['feature1','feature2']].values,y_train=df['target'].values)
# モデルを保存する
svm_util.save_model('svm_model.pkl')
# ------------------------------------------------------------------
# 新しいデータを作成し、保存したモデルを読み込んで分類を実行
# ------------------------------------------------------------------
# 新しいデータフレームを作成して予測を行う
new_data = {
'feature1': np.random.rand(10),
'feature2': np.random.rand(10)
}
new_df = pd.DataFrame(new_data)
# モデルを読み込む
svm_util.load_model('svm_model.pkl')
# 読み込んだモデルで予測する
new_predictions = svm_util.predict(column=['feature1', 'feature2'], df=new_df)
print(new_predictions)
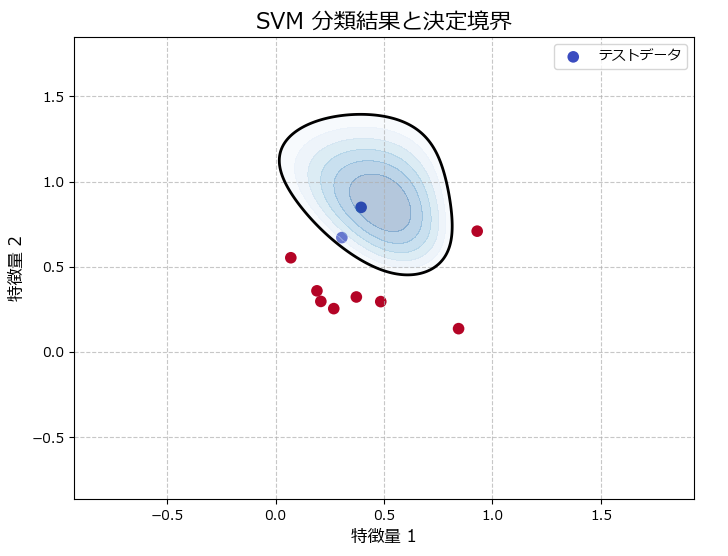
# テストデータの分類結果をグラフ化
plot_svm_results_2d(svm_util,X_test=new_df[['feature1','feature2']].values,y_test=new_predictions)[1 1 1 0 0 1 1 1 1 1 1 1 1 0 1 0 0 1 0 1 0 0 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1
1 1 0 0 1 1 1 1 1 0 0 1 1 1 1 1 1 0 1 1 0 1 0 1 1 1 1 1 0 1 1 1 1 0 1 1 1
0 1 0 1 0 1 1 1 0 1 1 0 0 0 1 1 1 0 0 0 1 1 0 0 1 1]
訓練データの分類結果
テストデータの分類結果
グラフ描画関数のリファレンスとソースコード
| OneClassSvm用グラフ描画関数 | 説明 |
|---|---|
| plot_ocsvm_results_1d( model, X_train=None, y_pred_train=None, X_test=None, y_pred_test=None ) | 1次元データのOne-Class SVMの結果をプロットする。学習データとテストデータを表示し、決定境界を描画する。 |
| plot_ocsvm_results( model, X_train=None, y_pred_train=None, X_test=None, y_pred_test=None ) | 2次元データのOne-Class SVMの結果をプロットする。学習データとテストデータを表示し、決定境界を描画する。 |
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'Meiryo'
def plot_svm_results_2d(model, X_train=None, y_train=None, X_test=None, y_test=None):
"""
2次元データのSVMの結果をプロットする。
学習データとテストデータを表示し、クラスを色分けしてプロットする。
また、決定境界を描画する。
Parameters:
model : SVMモデル
学習済みのSVMモデル。
X_train : array-like, shape (n_samples, 2), optional
学習データの特徴量。2次元データを想定。
y_train : array-like, shape (n_samples,), optional
学習データのクラスラベル。
X_test : array-like, shape (n_samples, 2), optional
テストデータの特徴量。2次元データを想定。
y_test : array-like, shape (n_samples,), optional
テストデータのクラスラベル。
"""
plt.figure(figsize=(8, 6))
# 学習データのプロット(2次元データのみ)
if X_train is not None and y_train is not None:
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap='coolwarm', edgecolors='k', s=70, label="学習データ")
# テストデータのプロット(2次元データのみ)
if X_test is not None and y_test is not None:
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap='coolwarm', edgecolors='none', s=70, label="テストデータ")
# 境界の等高線を描画するための範囲を設定
if X_train is not None:
xx, yy = np.meshgrid(np.linspace(X_train[:, 0].min() - 1, X_train[:, 0].max() + 1, 500),
np.linspace(X_train[:, 1].min() - 1, X_train[:, 1].max() + 1, 500))
elif X_test is not None:
xx, yy = np.meshgrid(np.linspace(X_test[:, 0].min() - 1, X_test[:, 0].max() + 1, 500),
np.linspace(X_test[:, 1].min() - 1, X_test[:, 1].max() + 1, 500))
else:
# 両方のデータがない場合は範囲を固定(適宜調整)
xx, yy = np.meshgrid(np.linspace(-5, 5, 500), np.linspace(-5, 5, 500))
x_range = np.c_[xx.ravel(), yy.ravel()]
Z = model.model.decision_function(x_range).reshape(xx.shape)
# 境界の等高線を描画
plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors='black')
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), 0, 7), cmap=plt.cm.Blues_r, alpha=0.3)
# グラフの設定
plt.legend()
plt.title("SVM 分類結果と決定境界", fontsize=16)
plt.xlabel("特徴量 1", fontsize=12)
plt.ylabel("特徴量 2", fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
# 結果を表示
plt.show()
def plot_svm_results_1d(model, X_train=None, y_train=None, X_test=None, y_test=None):
"""
1次元データのSVMの結果をプロットする。
学習データとテストデータを表示し、クラスを色分けしてプロットする。
また、決定境界を描画する。
Parameters:
model : SVMモデル
学習済みのSVMモデル。
X_train : array-like, shape (n_samples,), optional
学習データの特徴量。1次元データを想定。
y_train : array-like, shape (n_samples,), optional
学習データのクラスラベル。
X_test : array-like, shape (n_samples,), optional
テストデータの特徴量。1次元データを想定。
y_test : array-like, shape (n_samples,), optional
テストデータのクラスラベル。
"""
plt.figure(figsize=(8, 6))
# 学習データのプロット
if X_train is not None and y_train is not None:
plt.scatter(X_train, y_train, c='lightblue', edgecolors='k', s=70, label="学習データ")
# テストデータのプロット
if X_test is not None and y_test is not None:
plt.scatter(X_test, y_test, c='green', edgecolors='none', s=70, label="テストデータ")
# 決定境界の描画
if X_train is not None:
x_range = np.linspace(X_train.min() - 1, X_train.max() + 1, 500).reshape(-1, 1)
elif X_test is not None:
x_range = np.linspace(X_test.min() - 1, X_test.max() + 1, 500).reshape(-1, 1)
else:
# 両方のデータがない場合は固定範囲を使用(適宜調整)
x_range = np.linspace(-5, 5, 500).reshape(-1, 1)
y_range = model.model.decision_function(x_range)
plt.plot(x_range, y_range, color='black', linewidth=2, label='決定境界')
# グラフの設定
plt.axhline(0, color='black', linewidth=2)
plt.legend()
plt.title("SVM 分類結果(1次元)", fontsize=16)
plt.xlabel("特徴量", fontsize=12)
plt.ylabel("クラスラベル", fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
# 結果を表示
plt.show()SVMUtilクラスのリファレンスとソースコード
| SVMUtilのメソッド | 説明 |
|---|---|
| __init__(df=None, model_path=None) | クラスの初期化メソッド。データフレームとモデルパスを受け取る。 |
| fit( column, target, C=1.0, gamma="auto", kernel="rbf" ) | column: 特徴量(説明変数)のカラムリスト target: 目的変数(ターゲット変数)のカラム名 C: 誤分類の許容度。0.1~1000程度の範囲で指定 gamma: カーネルの広がり具合を制御するパラメータ 0.0001~10 程度の範囲で指定 |
| predict(column, df=None) | 学習したモデルを使用して予測を行うメソッド。指定したカラムを使用。 |
| read_csv(file_name, encoding="shift-jis") | CSVファイルからデータを読み込むメソッド。 |
| save_model(model_path) | 学習したモデルをファイルに保存するメソッド。 |
| load_model(model_path=None) | モデルをファイルから読み込むメソッド。 |
import numpy as np
import pandas as pd
from sklearn.svm import SVC
import pickle
class SVMUtil:
def __init__(self, df=None, model_path=None):
"""
SVMUtilクラスの初期化メソッド
:param df: 初期データフレーム (pd.DataFrame)
:param model_path: モデルファイルのパス (str)
"""
self.df = None if df is None else df.copy() # データフレームのコピーを保持
self.model = None if model_path is None else self.load_model(model_path) # SVMモデル
self.pred = [] # 予測結果のリスト
def fit(self, column, target, C=1.0, gamma="auto", kernel="rbf"):
"""
SVMモデルの作成と学習
:param column: 学習に使用するカラム名 (str または list)
:param target: 目的変数(ターゲット変数)のカラム名 (str)
:param C: SVMのCパラメータ (float)
:param gamma: SVMのgammaパラメータ (str または float)
:param kernel: 使用するカーネルの種類 (str)
- 'linear': 線形カーネル
- 'poly': 多項式カーネル
- 'rbf': RBFカーネル(ガウシアンカーネル⇒デフォルト)
- 'sigmoid': シグモイドカーネル
:return: 学習したモデル
"""
# 指定されたカラムのデータを抽出
if isinstance(column, list) and len(column) > 1:
X = self.df[column].values
else:
X = self.df[column].values.reshape(-1, 1) # 複数カラムのデータを2次元配列に変換
y = self.df[target].values
# SVMモデルの作成
self.model = SVC(C=C, gamma=gamma, kernel=kernel, probability=True).fit(X, y)
return self.model
def predict(self, column, df=None):
"""
学習したモデルを使用して予測を行う
:param column: 学習に使用するカラム名 (str または list)
:param df: 予測に使用するデータフレーム (pd.DataFrame)
:return: 予測結果の配列
"""
if df is not None:
self.df = df
# 指定されたカラムのデータを抽出
if isinstance(column, list) and len(column) > 1:
X = self.df[column].values
else:
X = self.df[column].values.reshape(-1, 1) # 複数カラムのデータを2次元配列に変換
self.pred = self.model.predict(X)
return self.pred
def read_csv(self, file_name, encoding="shift-jis"):
"""
CSVファイルからデータを読み込むメソッド
:param file_name: 読み込むファイルのパス (str)
:param encoding: ファイルのエンコーディング (str)
"""
self.df = pd.read_csv(file_name, encoding=encoding) # データフレームに読み込み
def save_model(self, model_path):
"""
学習したモデルをファイルに保存するメソッド
:param model_path: 保存するファイルのパス (str)
"""
self.model_path = model_path
with open(model_path, 'wb') as f:
pickle.dump(self.model, f) # モデルをバイナリ形式で保存
def load_model(self, model_path=None):
"""
モデルをファイルから読み込むメソッド
:param model_path: 読み込むファイルのパス (str)
:return: 読み込んだモデル
"""
if model_path is None:
model_path = self.model_path
with open(model_path, 'rb') as f:
self.model = pickle.load(f) # モデルをバイナリ形式で読み込み
return self.modelまとめ
本記事では、サポートベクターマシン(SVM)の概要とメリット、デメリット、得意なデータ、不得意なデータ、使い方と可視化について、一通り解説しました。また、コピペで使えるサンプルコードや、SVMが便利になる自作クラスについても紹介しました。
SVMは、高次元データや少量データでも高精度な分類や回帰、異常検知が可能な強力なアルゴリズムです。特にマージン最大化の考え方やカーネルトリックを活用することで、線形分離が難しいデータにも柔軟に対応できます。
一方で、大規模データには計算コストがかかりすぎる点や、ハイパーパラメータの調整が必要であるなどの課題も存在します。
SVMは、適切な場面で活用することで、製造業のデータ分析に大いに役立つものと思います。SVM実践の際には、是非この記事を参考にしてください。









コメント