ビジネスや科学、日常生活のあらゆる場面で、私たちは時間の経過とともに変化するデータに囲まれています。株価の変動、気温の推移、Webサイトへのアクセス数、工場の生産量など、これらはすべて「時系列データ」と呼ばれます。そして、この時系列データに潜むパターンや傾向を読み解き、未来を予測したり、異常を検知したりするための強力な手法が「時系列分析」です。
本記事では、時系列分析の基本から、異常検知・未来予測・データ補正の技術まで、Pythonによる具体的なコード例を交えながら、その活用方法を詳しく解説します。これから時系列分析を始める方は、是非参考にしてください。
時系列分析とは？
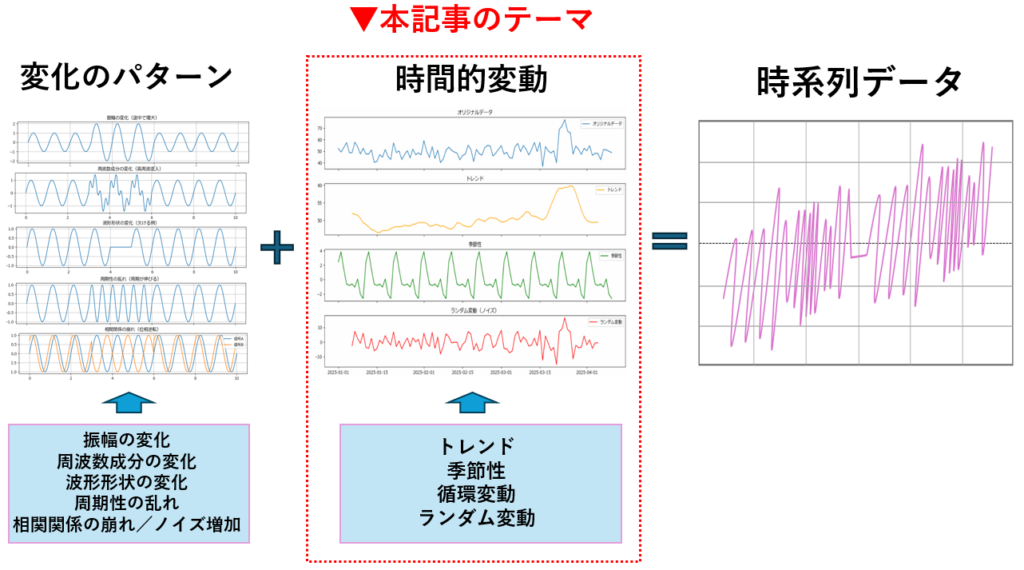
時系列分析とは、時間の経過とともに記録されたデータ（時系列データ）を分析し、そのデータに隠されたパターン、トレンド、季節性、周期性などを特定することで、将来の値を予測したり、異常を検知したり、過去の事象を深く理解したりする統計的・機械学習的なアプローチのことです。
通常のデータ分析が異なる点は、「時間」という要素がデータに不可欠な意味を持つことです。データの並び順が重要であり、過去のデータが未来のデータに影響を与えるという前提があります。
製造業における時系列データの具体的な例として、次のものがあります。
- 設備の稼働状況データ
稼働時間、停止時間、電力消費量、生産量、生産個数 - センサーデータ
温度、圧力、湿度、振動、電流、電圧、流量、液面レベル、画像・音声データ - 品質管理データ
不良率、歩留まり率、検査データ、クレーム発生件数 - 在庫・供給チェーンデータ
原材料の在庫量、部品の入荷数、出荷数、受注数、納期 - 環境・エネルギーデータ
工場内の温度・湿度、エネルギー消費量（ガス、水など）
これらの時系列データを分析することで、製造業は「勘と経験」に頼るだけでなく、データに基づいた客観的な意思決定を下し、競争力を高めることができます。例えば、センサーデータから設備の故障を予測し、計画的なメンテナンスを行う「予知保全」は、生産ラインの停止時間を大幅に削減し、生産効率を向上させる典型的な時系列分析の活用事例です。
時系列分析の仕組み
時系列分析は、後述する４つの構成要素に分解し、その特性に応じた方法で予測モデルを作成し、未来を予測します。
そして、この予測を使って異常検知やデータ補正／クリーニングを実現します。予測モデルの作成には、次の３つのステップが必要です。
異常検知は、未来予測した結果と実測値の乖離が、設定した閾値を超えたら異常値として判定します。
データ補正／クリーニングは、未来予測した結果と実測値の乖離が、設定した閾値を超えた部分を、予測値で置き換えます。
STEP1．時系列データに潜む「4つの構成要素」を理解する
時系列分析の第一歩は、目の前の時系列データがどのような要素で構成されているかを理解することです。どんなに複雑に見えるデータでも、多くの場合、以下の4つの要素に分解して考えることができます。
| 構成要素 | 説明 |
|---|---|
| トレンド （Trend） | 長期的にデータの値が増加・減少・横ばいする傾向のこと。一般的に、時系列の中で持続的な変化が見られるパターンです。 |
| 季節性 （Seasonality） | 一定の周期（例えば1年、1週間など）で繰り返されるパターン。気温の変化や曜日別の売上変動などが典型例です。 |
| 周期性 （Cyclicity） | 季節性と異なる点は、周期が必ずしも一定ではないこと。例えば、景気の循環や市場の大きな変動などが該当します。 |
| 不規則性 （Irregularity / Noise） | ランダムな変動や、一時的な異常値のこと。外的要因による変動（例えば、災害や突発的なイベントによる影響）も含まれることがあります。 |
STEP2．データを「分解」する
時系列分析では、まずこれらの要素をデータから分離する「分解（Decomposition）」という作業を行うことが一般的です。複雑な時系列データは、トレンド、季節性、不規則性の組み合わせとして表現できると考えます。
たとえば、ある商品の月間販売数データがあったとします。このデータには、長期的な売上成長（トレンド）、夏場に売上が伸びる傾向（季節性）、そして予測不能なイレギュラーな要因（不規則性）が混じっているかもしれません。
これらの要素を別々に抽出することで、
- 「長期的な成長はどのくらいか？」
- 「季節的なピークはいつで、どのくらいの規模か？」
- 「それ以外の予測できない変動はどのくらいか？」
といった洞察を得ることができます。これにより、データの全体像をより深く理解し、それぞれの要素に基づいて将来の予測や異常検知を行う準備が整います。
STEP3．データを「予測」する
データを分解し、その特性を理解した上で、いよいよ未来の値を予測したり、異常を検知したりするためのモデルを構築します。時系列分析は、「統計的手法」と「機械学習/深層学習モデル」の２つに分類できるので、それぞれ代表的なものを紹介しておきます。
統計的手法
| 手法 | 仕組み | 用途 | メリット | デメリット |
|---|---|---|---|---|
| 移動平均（MA） | 過去 n 期間の平均値を計算し、次の予測値とする。 | データの平滑化、短期的なトレンドの把握 | シンプルで直感的、ノイズ除去に効果的 | 急激な変化に対する予測精度が低い |
| 指数平滑化法（ES） | 直近のデータに高い重みを与えて平均化 | 短期～中期予測、トレンドや季節性のあるデータ | 最近のデータの影響を強く反映、適応力が高い | 長期予測には不向き、パラメータ調整が必要 |
| ARIMAモデル | 自己回帰（AR）+ 階差（I）+ 移動平均（MA） | トレンドや季節性のある時系列データの予測 | 強力な統計モデル、過去のパターンを学習できる | モデルの選択やパラメータチューニングが難しい |
| SARIMA | ARIMAに季節性の要素を加えた拡張モデル | 季節性の強いデータの予測（売上、気温など） | 季節変動を考慮できる | モデルが複雑化しやすい、周期性の設定が重要 |
指数平滑化（ES） には「単純指数平滑化（SES）」「二重指数平滑化（DES）」「三重指数平滑化（TES）」があり、TESは季節性のあるデータに適しています。
ARIMA は定常性が前提なので、非定常なデータには「差分を取る」ことで対応する必要があります。
SARIMA は売上データのように毎年特定の時期にピークがある場合に有効です。
機械学習/深層学習モデル
| 手法 | 仕組み | 用途 | メリット | デメリット |
|---|---|---|---|---|
| プロフェット（Prophet） | トレンド・季節性・イベントをモデル化 | 明確な季節性や祝日の影響を受けるデータ | 直感的に使える、デフォルト設定でも良好 | 複雑な時系列データには不向き、細かな調整が必要 |
| ランダムフォレスト / GBDT | 多くの決定木を組み合わせて予測 | 特徴量設計が必要な時系列データ | 非線形な関係性を学習可能 | 時系列の順序性を直接学習できない、特徴量設計が必須 |
| LSTM（長・短期記憶ネットワーク） | 長期的な依存関係を学習する深層学習モデル | 複雑なパターンを持つ時系列データ | 長期的なトレンドを学習可能 | 訓練に大量のデータが必要、計算コストが高い、解釈が難しい |
プロフェット（Prophet） はトレンド・季節性・イベントの影響を考慮しながら、直感的なパラメータ調整で予測できますが、市場変動や株価のような不規則なデータには不向きです。
ランダムフォレスト / GBDT は時系列データを直接扱うのではなく、特徴量（過去の値、曜日、月など）を設計することで予測を行います。
LSTM はRNN（リカレントニューラルネットワーク）の一種で、長期的な依存関係を学習できますが、データ量が少ないと効果が低くなり、計算コストが高くなります。
製造業での時系列分析事例
| 目的・課題 | 時系列データの利用例 | 時系列分析でできること | 主なメリット |
|---|---|---|---|
| 故障予知・予知保全 | 設備の振動、温度、電流などのセンサーデータ | 故障の兆候を早期検知し、計画的なメンテナンスを行う | 予期せぬ設備停止の削減、メンテナンスコストの最適化 |
| 生産計画の最適化 | 製品の過去の販売実績、受注データ、在庫データ | 将来の需要を予測し、最適な生産・在庫計画を立てる | 過剰在庫・欠品リスクの削減、生産効率の向上 |
| 品質管理・歩留まり改善 | 生産ラインの温度、圧力などのセンサーデータ、不良率 | 品質異常をリアルタイムで検知し、不良品の発生を未然に防ぐ | 製品不良率の低減、歩留まり向上、クレーム減少 |
| エネルギーコスト削減 | 工場全体の電力消費量、各設備の電力消費量 | 電力消費パターンを予測し、無駄な電力使用を特定・削減する | エネルギーコストの削減、環境負荷の低減 |
| 業務改善・効率化 | 稼働時間、作業時間、ボトルネック工程の生産実績 | 生産プロセスのボトルネックを特定し、作業効率を向上させる | 生産性向上、人件費の最適化、生産リードタイム短縮 |
時系列分析のメリット・デメリット
時系列分析のメリット
- 未来予測が可能
時系列分析は、過去・現在のデータからトレンドや季節性、周期性といったパターンを抽出することで、将来の動向を予測できます。 - 異常検知と故障予知ができる
ノイズや外れ値の検出により、設備故障や品質低下などのリスク要因を早期にキャッチできます。 - データのパターン理解とインサイトの獲得
トレンド、季節性、循環性、不規則性といった要素により、データの背後にある動向や根本原因が明らかになります。 - リアルタイムデータへの適用性
Webアクセス数や株価のように、連続的・リアルタイムで生成されるデータに対しても、適切な手法と前処理を施すことで即時の分析が可能です。 - 汎用性の高さ
統計的手法（移動平均、指数平滑化、ARIMAなど）から、機械学習・深層学習モデル（Prophet、LSTMなど）まで、さまざまな手法が存在するため、データの特性や業務要件に応じたモデル選定がしやすいという特徴があります。
時系列分析のデメリット
- データ前処理の必要性
時系列分析では、データのクレンジング（外れ値や欠損値の補正、データの整形）が非常に重要です。 - 非定常性への対応が必須
多くの時系列モデル（たとえばARIMA）は、定常性を前提として設計されています。 - 短期予測と長期予測の不確実性
短期間の予測では比較的高い精度が期待できますが、長期予測になると不確実性が増し、予測の信頼性が低下する場合があります。 - モデル選定とパラメータ調整の難しさ
数多くの手法が存在する中で、データの性質に最適なモデルを選ぶことは容易ではありません。 - 過剰適合や誤検出のリスク
複雑なモデルを使用すると、データのノイズや一時的な変化に過剰に適合し、実際のパターンを見逃す可能性があります。
時系列分析に適したデータ・適さないデータ
時系列分析に適したデータ
- 連続性と一定の観測間隔ポイント
データが毎日、毎週、もしくは毎月など、規則的な間隔で取得されていると、トレンドや季節性がより正確に抽出されやすくなります。 - 十分な履歴（長期間のデータ）
長期にわたるデータがあると、周期性やトレンドをしっかり把握できます。 - 明確なパターンや周期性
気温、売上、アクセス数など、時間とともに変化するパターンが存在する場合、季節性や周期性を活かした予測、異常検知が容易になります。 - 適度なノイズレベル
自然な測定誤差や外部要因による変動は、学習をより強固なものにしてくれますが、根本的なパターンを覆い隠さない程度である必要があります。 - 外れ値や欠損値が少ない
測定エラーや外れ値が少なく、データがクリーンであるほど効果的に学習が進みます。
時系列分析に適さないデータ
- 観測間隔が不規則
データ収集が不均一な場合、時間軸上のパターンが歪み、トレンドや季節性の抽出が困難となります。 - 短期間のデータ
過去の履歴が短いと、長期的なトレンドや周期性を十分に捉えられません。 - 極端にノイズが多いデータ
ノイズレベルが極めて高い場合、実際のパターンを見出すのが非常に難しく、誤った予測につながる恐れがあります。 - 大量の外れ値や欠損値が含まれるデータ
外れ値や欠損値が多いと、モデルが誤った方向に学習してしまい、予測の信頼性が大幅に低下します。 - 突発的なイベントによる非定常な変動
自然災害、特別なプロモーション、突発的な故障など、一時的で極端な影響が表れると、通常の時系列モデルでは対処が難しい場合があります。
サンプルデータの作成
本記事で使うサンプルデータの作成プログラムを紹介しておきます。
記事内で紹介するプログラムを実行したい場合は、あらかじめ下記のプログラムを用いてデータを作成しておいてください。
import numpy as np
import pandas as pd
# 時系列データを生成
np.random.seed(42)
time = pd.date_range(start="2025-01-01", periods=100, freq="D")
normal_values = np.random.normal(loc=50, scale=5, size=100) # 正常データ
anomaly_values = normal_values.copy()
anomaly_values[80:85] += 20 # 異常データの追加
df = pd.DataFrame({"timestamp": time, "value": anomaly_values})
df.to_csv("dummy_timeseries.csv", index=False)データを4つの要素に分解する
時系列データを トレンド (Trend)、季節性 (Seasonality)、循環変動 (Cyclic Variation)、ランダム変動 (Irregular Variation) の 4つの要素に分解 するには、statsmodels の seasonal_decompose() を使用します。
seasonal_decompose() は、時系列データを 加法モデル (Additive) または 乗法モデル (Multiplicative) に基づいて分解します。
| 引数名 | 意味 |
|---|---|
| model | 時系列データの分解方法で、"additive"か"multiplicative"のどちらかを指定します。 各要素が「加算的」に影響する加法モデル（例：気温の変化など）→ model="additive"各要素が「乗算的」に影響する乗法モデル（例：売上データなど）→ model="multiplicative" |
| period | データ内の繰り返しパターンの長さ＝季節性の周期 (Seasonality Period) を指定します。 月単位のデータ → period=12（1年を12か月として考える）週単位のデータ → period=7（1週間の周期として考える）営業日データ → period=5（1週間のうち5日が営業日） |
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose
from matplotlib import rcParams
# 日本語フォントの設定
rcParams['font.family'] = 'Meiryo'
def decompose_time_series(df, timestamp_col, value_col, model="additive", period=10):
"""
時系列データを分解し、トレンド・季節性・ランダム変動をプロットする。
Parameters:
df (pd.DataFrame): 時系列データのDataFrame
timestamp_col (str): 時刻のカラム名
value_col (str): 分解対象の数値データのカラム名
model (str): "additive" または "multiplicative"
period (int): 季節性の周期（データの特性に応じて調整）
Returns:
None (グラフを表示)
"""
# 時系列データを設定
df = df.copy() # 元のデータを変更しないようにコピー
df.set_index(timestamp_col, inplace=True)
# 時系列分解
result = seasonal_decompose(df[value_col], model=model, period=period)
# 分解結果をプロット
fig, axes = plt.subplots(4, 1, figsize=(12, 8), sharex=True)
axes[0].plot(df.index, df[value_col], label="オリジナルデータ")
axes[0].set_title("オリジナルデータ")
axes[1].plot(df.index, result.trend, label="トレンド", color="orange")
axes[1].set_title("トレンド")
axes[2].plot(df.index, result.seasonal, label="季節性", color="green")
axes[2].set_title("季節性")
axes[3].plot(df.index, result.resid, label="ランダム変動", color="red")
axes[3].set_title("ランダム変動（ノイズ）")
for ax in axes:
ax.legend()
plt.tight_layout()
plt.show()
if __name__ == "__main__":
# CSVを読み込んで関数を実行
df = pd.read_csv("dummy_timeseries.csv", parse_dates=["timestamp"])
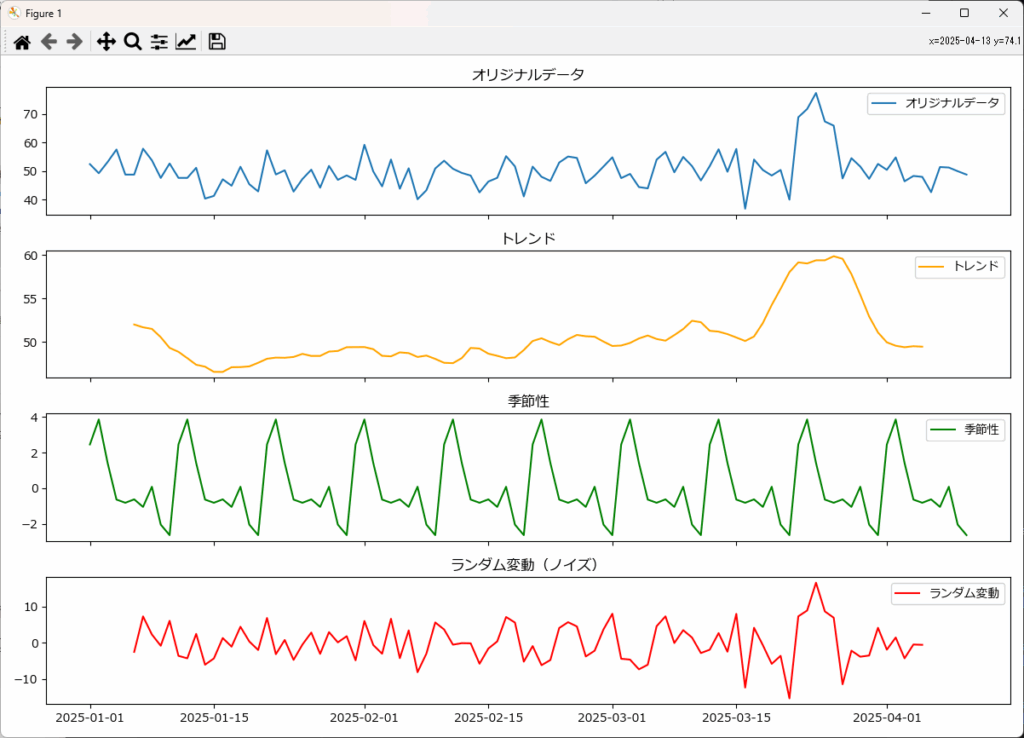
decompose_time_series(df, "timestamp", "value", model="additive", period=10)グラフから次のことが分かります。
- 明確な上昇トレンド: 全体的に増加傾向だが、後半で急激に上昇する「変化点」が存在する。
- 明確な周期的な季節性: 規則正しい上下の変動が見られる。
- ランダムなノイズ: 全体的に明確なパターンが見られないが、一部異常な変動がある。
- データ期間: 3ヶ月程度と比較的短期（2025-01-01から2025-04-01）。
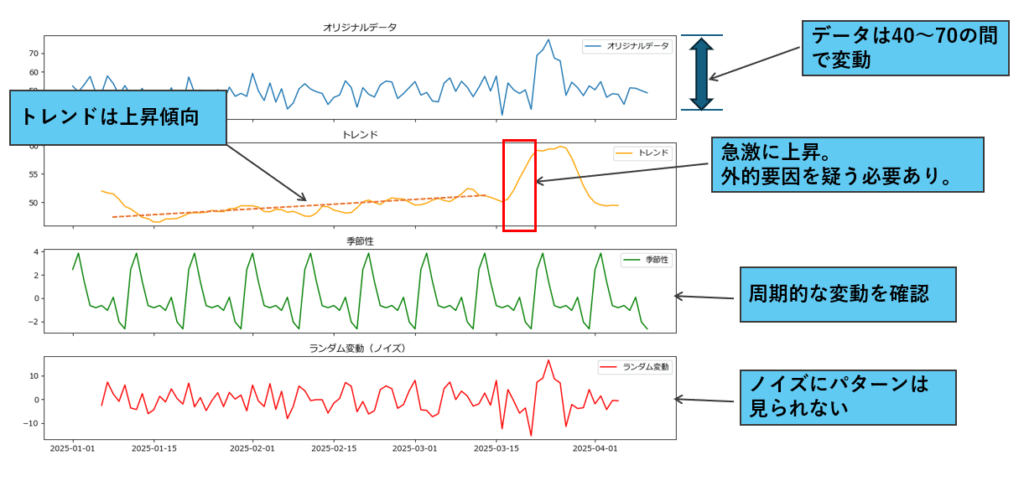
このデータには明確なトレンドと周期性（季節性）があるため、異常検知モデルは ARIMAの拡張であるSARIMA（Seasonal ARIMA）、もしくはProphet が第一候補に挙げられます。
異常検知には、移動平均、指数平滑化法、ARIMAなど、いくつもの種類のモデルがあり、モデルごとに異常検知の結果が異なります。
時系列データは、４つの要素（トレンド、季節性、周期性、不規則性）が複雑に絡み合ったデータです。どの部分に着目し、どこまでを異常として捉えるかによって、同じデータであっても異常の答えは変わります。
時系列の異常検知は、４つの要素を理解したうえで異常とは何かを定義し、それに最もふさわしいモデルを選ぶ必要があります。
時系列データ分析で使われる主な手法
移動平均（MA）: シンプルなトレンド分析ツール
移動平均（MA）は、過去の一定期間のデータの平均を計算し、変動の傾向を滑らかにする方法です。シンプルながら有効な分析手法であり、特に短期的な市場トレンドを把握するのに適しています。
但し、移動平均では未来予測ができません。移動平均は過去の値を使うため、値が存在しない未来は計算の術がありません。
用途
- 株価のトレンド分析（短期・中期の市場動向を視覚化）
- 売上データの変動の把握（季節要因の影響をスムーズにする）
- 経済指標の傾向分析（景気動向の基礎評価）
実務でのポイント
✔ 移動平均の期間選定: 短期（5日など）は敏感に反応、長期（50日など）は安定したトレンド把握向け。
✔ 併用する分析手法: 単独では限界があるため、ボリンジャーバンドなどと組み合わせると効果的。
✔ 急激な変化には非対応: 突発的な市場変動には、指数平滑化など別の手法を検討する。
メリット
✅ シンプルで分かりやすい
✅ ノイズ除去に有効
✅ 様々な業界で活用可能
デメリット
❌ 急な変化を捉えにくい
❌ 未来予測には不向き
❌ 季節性が強い場合は補助的に使うべき
指数平滑化法（ES）: 変化を敏感に捉える予測手法
指数平滑化（ES）は、直近のデータに重みを置きながら平均を計算することで、最新のトレンドを反映しやすくする手法です。移動平均に比べて、最近の変化をより迅速に捉えられます。
用途
- 在庫管理（販売傾向を考慮して適切な発注量を決定）
- 需要予測（製品の売れ行き変化を早期に察知）
- 財務データ分析（売上や収益の変動をリアルタイムで評価）
実務でのポイント
✔ α（平滑化係数）の設定: 0.1～0.3が一般的（数値が大きいほど最近のデータを強く反映）。
✔ 長期予測は不向き: 短期間のトレンド把握に特化。
✔ 急激な変化のあるデータに適用: 例えばプロモーションによる売上増減をすぐに捉えられる。
メリット
✅ 最新データを迅速に反映
✅ シンプルな計算で導入しやすい
✅ 在庫管理や短期予測で高い精度
デメリット
❌ 長期間の予測には不適
❌ トレンドの変化に過敏になりすぎることも
❌ 係数の選定が結果に大きく影響
ARIMAモデル: 本格的な時系列予測の標準技術
ARIMA（自己回帰・差分・移動平均）モデルは、時系列データのパターンを分析し、未来を予測する統計的手法です。データの傾向や周期性を考慮し、長期予測にも対応可能な高度なモデル。
用途
- 経済予測（GDPやインフレ率の変動分析）
- 気象データ分析（降水量や気温変動の予測）
- 販売量予測（小売業やECサイトのデータ分析）
実務でのポイント
✔ データの前処理が重要: トレンドや季節性の有無を事前に確認し、適切な差分化を行う。
✔ パラメータ調整（p,d,q）: 自動調整ツールを活用することで手間を削減可能。
✔ ノンステーショナリティ対策: データが非定常の場合は適切な変換を行う。
メリット
✅ トレンドや周期性を考慮できる
✅ 短期・長期予測の両方に対応
✅ 多くの分野で採用されている
デメリット
❌ モデルの調整に専門知識が必要
❌ 計算負荷が高い（大規模データには工夫が必要）
❌ 複雑な時系列パターンには限界も
SARIMA: 季節性を考慮した時系列予測
SARIMA（Seasonal ARIMA）は、ARIMAモデルに季節要因を組み込み、周期的な変動を考慮した予測を行う手法です。季節パターンのあるデータに適しています。
用途
- 売上予測（季節ごとの需要変動を考慮）
- 気温・降水量予測（周期的な気象変動の分析）
- 観光業の需要予測（繁忙期・閑散期の動向分析）
実務でのポイント
✔ データの周期性の確認: 季節要因（例えば12か月周期）を事前に把握。
✔ 適切なパラメータ設定: ARIMAの基本設定に加え、季節性パラメータを考慮する。
✔ 計算負荷が高い: 特に長期間のデータには処理が重くなるため注意。
メリット
✅ 季節変動を考慮した予測が可能
✅ 短期・長期のトレンド分析に適用可能
✅ 小売業や気象予測で広く活用されている
デメリット
❌ モデル構築が難しく、専門知識が必要
❌ 計算負荷が高く、リソースを消費しやすい
❌ 定期的な再調整が必要
プロフェット（Prophet）: 直感的な時系列予測ツール
Prophetは、Facebookが開発した時系列予測モデルで、トレンドと季節性を考慮しながら自動でパラメータ調整を行うツールです。特にデータサイエンスの初心者に優しい設計になっています。
用途
- 売上予測（トレンドの変化を把握）
- Webトラフィック予測（ユーザー行動の変化を分析）
- イベント影響分析（セールや広告キャンペーンの効果を予測）
実務でのポイント
✔ 少ないデータでも対応可能: 短期間のデータでも有効。
✔ 簡単に適用できる: 複雑な調整なしで利用可能。
✔ 高度なカスタマイズには限界: 独自の特性を持つデータには調整が必要。
メリット
✅ 設定が容易で初心者にも使いやすい
✅ トレンド・季節性を自動で調整
✅ 短期間で高精度な予測が可能
デメリット
❌ 過度に単純化されることがある
❌ 複雑なデータには適用しづらい
❌ 詳細な調整ができない場面もある
ランダムフォレスト / GBDT: 機械学習による高精度予測
ランダムフォレストやGBDT（勾配ブースティング決定木）は、複数の決定木を組み合わせ、複雑なデータの予測精度を向上させる機械学習手法です。
用途
- 製品の需要予測（多変量データを活用）
- 金融市場分析（株価の変動要因を考慮）
- リスク管理（不正検出やクレジットスコアリング）
実務でのポイント
✔ 特徴量の選定が重要: 関連性のあるデータを適切に選択する。
✔ 過学習に注意: 過剰に学習すると、汎用性が低下する。
✔ 解釈性が低い: モデルの内部構造がブラックボックス化しやすい。
メリット
✅ 非線形データの予測が得意
✅ 高精度な予測が可能
✅ 自動で重要な特徴を抽出
デメリット
❌ 計算コストが高く、処理速度が遅いことがある
❌ モデルの解釈が難しい
❌ 適切なパラメータ調整が必要
LSTM（長・短期記憶ネットワーク）: 深層学習による時系列予測
LSTM（Long Short-Term Memory）は、ニューラルネットワークの一種で、長期的な依存関係を学習できる時系列モデルです。従来の統計モデルよりも柔軟な予測が可能。
用途
- 音声認識（過去の言葉の流れを理解）
- 金融市場予測（株価の変動要因を分析）
- 自然言語処理（文脈を考慮した文章生成）
実務でのポイント
✔ 大量のデータが必要: 少量のデータでは精度が低くなる。
✔ 計算リソースの確保: GPUを活用すると学習速度が向上。
✔ ハイパーパラメータの調整: 学習率やレイヤー数の設定が重要。
メリット
✅ 長期間のデータ関係を学習可能
✅ 高度なパターン認識に適している
✅ ディープラーニングの利点を活用可能
デメリット
❌ 訓練に大量のデータと計算リソースが必要
❌ 過学習のリスクがある
❌ 適切なモデル調整に時間がかかる
まとめ
本記事では、Pythonを用いた時系列データ分析の基本から応用までを解説しました。ARIMAや指数平滑化法、LSTMといった代表的な手法を通じて、予測・異常検知・補正といった実務で役立つ分析アプローチを紹介しました。
時系列データは、センサーの計測値や業務のログ、売上など、あらゆる分野に存在します。これらを適切に分析することで、将来の動きを予測したり、異常値をいち早く検知したり、データの欠損やノイズを補正することが可能になります。
Pythonには、時系列分析に適したライブラリやフレームワークが豊富に揃っており、誰でも手軽に高度な分析を行うことができます。本記事で紹介した内容を参考に、ぜひ実データに挑戦してみてください。
コメント